1. Main traversal methods of binary tree

(1) Depth first traversal: traversal goes to the depth of the tree and returns when a leaf node is encountered. It can be implemented by recursion or iteration. Recursion is generally used to simulate the process of traversing deep.

        It can be further divided into pre order traversal, middle order traversal and post order traversal.

Preorder traversal: first traverse the intermediate node, then the left node, and finally the right node. (middle left and right)

Similarly, middle order traversal: left, middle and right; Post order traversal: left and right middle.

The judgment skill is: the position of the intermediate node is the traversal order. For example, if the middle node is in the left and right, and the middle node is in the front, it is the front order; Left, middle and right, and the middle node is in the middle, which is the middle order; In the left and right, in the middle, at the end, is the post order traversal.

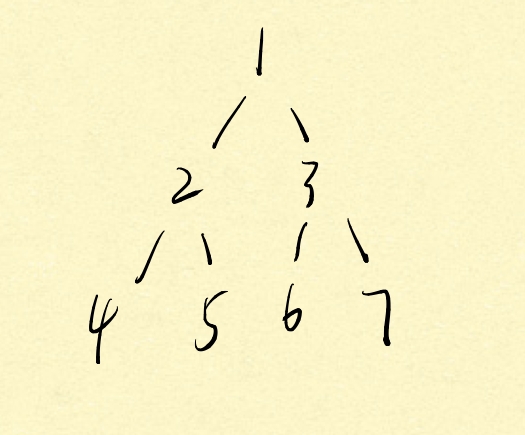
  For example, this binary tree:

Preorder traversal: [1, 2, 3, 4, 5, 6, 7]

Middle order traversal: [4, 2, 5, 1, 6, 3, 7]

Post order traversal: [4, 5, 2, 6, 7, 3, 1]

(2) Breadth first traversal: start from the root node and traverse layer by layer. It is generally realized by iterative method.

2. Implementation code

  Definition of node class:

public class TreeNode {
    int val;
  	TreeNode left;
  	TreeNode right;
  	TreeNode() {}
  	TreeNode(int val) { this.val = val; }
  	TreeNode(int val, TreeNode left, TreeNode right) {
    		this.val = val;
    		this.left = left;
    		this.right = right;
  	}
}

(1) Depth first traversal

① Recursive method  

Preorder traversal: Idea: exit the recursive function of this layer when encountering an empty node, and then process the intermediate node, left node and right node accordingly. The intermediate node directly adds to the result set, and then recurses to the left and right in turn.

public List<Integer> preOrderReverse(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        preOrder(root, (ArrayList<Integer>) res);
        return res;
    }

    void preOrder(TreeNode root, ArrayList<Integer> res){
        if(root==null){
            return;    //Null node encountered, return
        }
        res.add(root.val);           // Middle: add nodes to the result array
        preOrder(root.left, res);    // Left: traverse the left node of the current node
        preOrder(root.right, res);   // Right: traverse the right node of the current node
    }

The middle order and post order traversal are the same. Just put the processing logic of the intermediate node in the middle and behind the processing logic of the left and right nodes respectively.

② Iterative method

Preorder traversal / postorder traversal: the code of preorder and postorder traversal is similar by iterative method. It needs to be implemented with the help of stack: pre order traversal. The right node enters the stack first and the left node enters the stack later (first in and then out, so it is the opposite of the traversal order).

public List<Integer> preOrderReverse2(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        if(root==null){
            return res;
        }
        Stack<TreeNode> stack = new Stack<>();    
        stack.push(root);   //Root node stack first
        while(!stack.isEmpty()){
            TreeNode node = stack.pop();
            res.add(node.val);    // Middle: node values are added to the result set
            if (node.right!=null) {
                stack.push(node.right);    //Left: right node stack
            }
            if(node.left!=null){
                stack.push(node.left);     //Right: left node stack
            }
        }
        return res;
        }

Middle order traversal: the iterative method of middle order traversal needs to use the traversal of the pointer to access the node and process the elements on the node with the help of the stack.

public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        if(root==null){
            return res;
        }
        Stack<TreeNode> stack = new Stack<>();
        TreeNode cur = new TreeNode();
        cur = root;    // Initialization pointer: points to the root node
        while(!stack.isEmpty() || cur!=null){
            if(cur!=null){    
                stack.push(cur);
                cur = cur.left;    // Left: iterate to the left leaf node
            }else{
                cur = stack.pop();
                res.add(cur.val);  // Medium: add result set
                cur = cur.right;   // Right: iterate to the leaf node on the right
            }
        }
        return res;

(2) Breadth first traversal

With the help of queues. The elements of each layer are stored in the queue. Each traversal of the queue is equivalent to traversing the elements of one layer of the binary tree. In the process of traversal, the left and right child nodes of the currently traversed node are added to the queue every time. Therefore, after traversing the nodes of this layer, the elements in the queue are the nodes of the next layer.

public List<List<Integer>> levelOrder(TreeNode root) {
        List<List<Integer>> res = new ArrayList<>();
        if(root==null){
            return res;
        }
        Queue<TreeNode> queue = new LinkedList<>();
        queue.add(root);        // The root node joins the queue first
        while (!queue.isEmpty()){
            int n = queue.size();    //Number of elements in the queue: equal to the number of elements in this layer
            List<Integer> temp = new ArrayList<>();    //temp stores the elements traversed by this layer
            for(int i=0; i<n; i++){
                TreeNode node = queue.poll();
                temp.add(node.val);    // The value of the element traversed by this layer is added to temp
                if(node.left!=null){
                    queue.add(node.left);    // The left node joins the queue
                }
                if (node.right!=null){
                    queue.add(node.right);   // The right node joins the queue
                }
            }
            res.add(temp);
        }
        return res;