Leetcode84

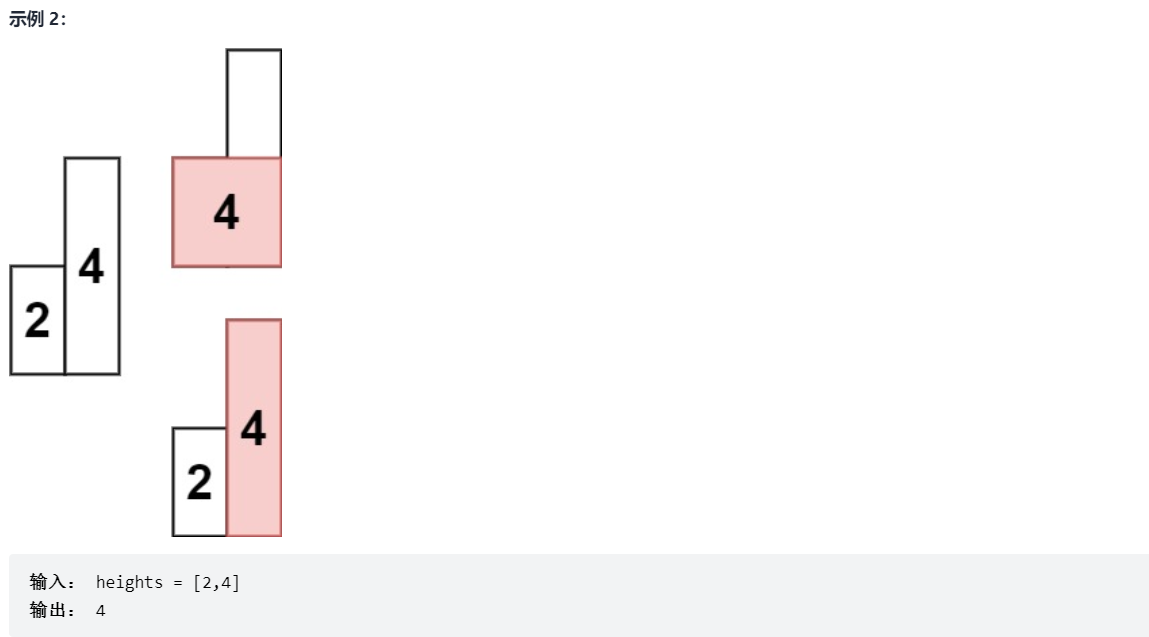
1. Problem description

2. Solutions

Solution 1: double pointer (O(n^2) timeout) (thinking about a solution to the problem

1. I can understand it by looking at the figure. For each column, the largest rectangle containing this column is the area between the first smaller column on the left and right, and then find the maximum value for no column, which will ensure to find the answer
2. To be honest, I can think of this degree. Although the double pointer has not been passed, the problem has been basically solved, that is, find the first number smaller than it on the left and right respectively
3. (thinking about problem solutions!!!!!! how can you think of this step? The examples given by the problem are not very common. We must give examples ourselves if we want to summarize or see them. For example, if you see that the examples of the problem are small on the left and large on the right, why don't you think about what the maximum values of grooves or protrusions are like, Take the example of the big side and the small side, and the groove protrusion, and you can sum it up. Originally, find the first small number on both sides, and the middle contains the maximum value of the current column!!!!!

class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        int Max=-1;
        for(int i=0;i<heights.size();i++){
            int left=i-1;
            int right=i+1;
            for(;left>=0;left--){
                if(heights[left]<heights[i]) break;
            }
            for(;right<heights.size();right++){
                if(heights[right]<heights[i]) break;
            }
            Max=max(Max,(right-left-1)*heights[i]);
        }
        return Max;
    }
};

Solution 2: dynamic programming (the idea of jump saving calculation is worth learning!!!)

Ideas and thoughts:

1. And the previous question [Leetcode monotone stack] 42. Connect rainwater (with dp optimized double pointer calculation!! double pointer, dynamic programming, monotone stack!!) The double pointer of dp optimization is the same, but the dp of the previous question is more conventional. This question has a little skill. The previous question records the value and this question records the subscript index, but they all save calculation!
2. The dp of this question is through the first small subscript index on the right recorded before, and then jump to compare. If some intermediate values are certainly greater than height[i], there is no need to compare. The picture has made it clear
3. This idea of jump saving calculation is very worthy of reference!!!!!

Code implementation:

1. The code implements initialization. Note that this initialization is very useful. If i==1, you will find that it must be initialized to - 1 and heights.size(), otherwise it will be an endless loop, and the practical significance is also - 1 or height.size(), which means that there is no smaller on the left or right, and the length of the interval just meets the conditions
2. If you meet the same elements, you have to look forward. Just give an example!

//while(t>=0&&heights[t]>heights[i]) t=leftFirstMin[t];
while(t>=0&&heights[t]>=heights[i]) t=leftFirstMin[t];

class Solution1 {
public:
    int largestRectangleArea(vector<int>& heights) {
        //1. [0, itself) the first small index on the left (itself, heights.zie()] the first small index on the right
        //This initialization is very useful. When i==1, you will find that it must be initialized to - 1 and heights.size(), otherwise it will be an endless loop
        //And in practical sense, - 1 or height.size() means that there is nothing smaller than yourself on the left or right, and the length of the interval just meets the conditions
        vector<int> leftFirstMin(heights.size(),-1);
        vector<int> rightFirstMin(heights.size(),heights.size());
        //2.
        for(int i=1;i<heights.size();i++){
            int t=i-1;
            //while(t>=0&&heights[t]>heights[i]) t=leftFirstMin[t];
            while(t>=0&&heights[t]>=heights[i]) t=leftFirstMin[t];
            leftFirstMin[i]=t;
        }
        for(int i=heights.size()-2;i>=0;i--){
            int t=i+1;
            //while(t<=heights.size()-1&&heights[t]>heights[i]) t=rightFirstMin[t];
            while(t<=heights.size()-1&&heights[t]>=heights[i]) t=rightFirstMin[t];
            rightFirstMin[i]=t;
        }
        //3.
        int Max=-1;
        for(int i=0;i<heights.size();i++){
            Max=max(Max,heights[i]*(rightFirstMin[i]-leftFirstMin[i]-1));
        }
        return Max;

    }
};

Solution 3: monotone stack

reflection:

1.[Leetcode monotone stack] 42. Connect rainwater (with dp optimized double pointer calculation!! double pointer, dynamic programming, monotone stack!!) Is to find the first column on the left and right sides of each column that is greater than the height of the column, and this problem is to find the first column on the left and right sides of each column that is smaller than the column.
2. Here comes to the important property of monotone stack, that is, whether the order in monotone stack is from small to large or from large to small [Leetcode monotone stack] 42. Connect rainwater (with dp optimized double pointer calculation!! double pointer, dynamic programming, monotone stack!!) In, I explained that the order of the monotonous stack receiving rain from the top of the stack (elements pop up from the top of the stack) to the bottom of the stack should be from small to large. Then, because the problem is to find the first column on the left and right sides of each column that is smaller than the column, the order from the top of the stack (elements pop up from the top of the stack) to the bottom of the stack should be from large to small!
3. The top of the stack, the next element at the top of the stack and the three elements to be put into the stack constitute the height and width of the maximum area we require. In fact, a convex is the maximum area we require! (how did you think of this convex? There is a reflection and summary of the above double pointer method!!)

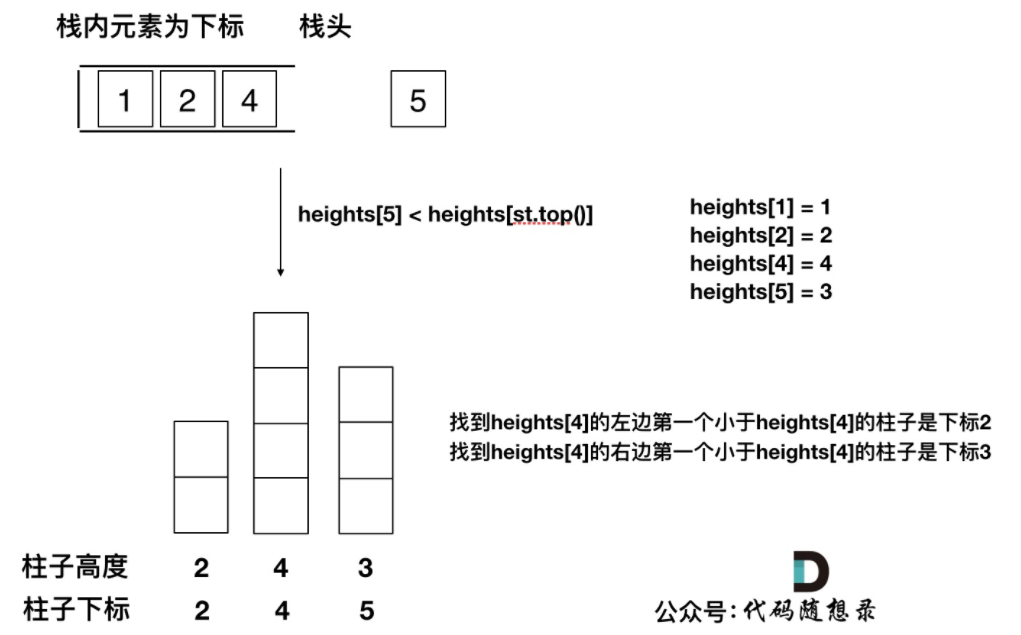
Code implementation 1: secondary check

1. It's good to find out the three situations in the code implementation. It's a common saying that it belongs to yes. The third one is to note that the values of left and right are the maximum area of a convex.
2. In one case, there is an increasing sequence left at the end, that is, there is no smaller one on the right. It keeps increasing, 1, 2, 4, 5, 6... So in fact, it's good to check it again. Think about left and right!!

class Solution2 {
public:
    int largestRectangleArea(vector<int>& heights) {
        //Increment stack ↑
        stack<int> stack;
        //Build monotone stack
        stack.push(0);
        int Max=-1;
        for(int i=1;i<heights.size();i++){
            //1.
            if(heights[stack.top()]<heights[i]){
                stack.push(i);
                continue;
            }
            //2.
            if(heights[stack.top()]==heights[i]){
                stack.push(i);
                continue;
            }
            //3.
            if(heights[stack.top()]>heights[i]){
                while(stack.empty()== false&&heights[stack.top()]>heights[i]){
                    int mid=stack.top(); stack.pop();
                    int left;
                    int right=i;
                    if(stack.empty()== false) left=stack.top();
                    else left=-1;
                    Max=max(Max,heights[mid]*(right-left-1));
                }
                stack.push(i);
            }
        }
        //If the stack is not empty, it proves that there is an increasing sequence in it, which means that there is no smaller value on the right than them
        //That's right=height.size()
        //left is the previous element in the stack
        while(stack.empty()== false){
            int mid=stack.top(); stack.pop();
            int left;
            int right=heights.size();
            if(stack.empty()== false) left=stack.top();
            else left=-1;
            Max=max(Max,heights[mid]*(right-left-1));
        }
        return Max;
    }
};

Code implementation 2: insert 0 from beginning to end to avoid secondary inspection

Insert 0 from the beginning to the end. Generally, just remember it. After analysis, adding 0 will clear the remaining incremental sequences, and the left and right are just right. Seconds!

class Solution3 {
public:
    int largestRectangleArea(vector<int>& heights) {
        //Increment stack ↑
        stack<int> stack;
        heights.insert(heights.begin(),0); //-----Change 1
        heights.push_back(0);
        //Build monotone stack
        stack.push(0);
        int Max=0; //int Max=-1; / / ----- change 2
        for(int i=1;i<heights.size();i++){
            //1. Situation 1
            if(heights[stack.top()]<heights[i]){
                stack.push(i);
                continue;
            }
            //2. Situation 2
            if(heights[stack.top()]==heights[i]){
                stack.push(i);
                continue;
            }
            //3. Situation 3
            if(heights[stack.top()]>heights[i]){
                while(stack.empty()== false&&heights[stack.top()]>heights[i]){
                    int mid=stack.top(); stack.pop();
                    int left;
                    int right=i;
                    if(stack.empty()== false) left=stack.top();
                    else left=-1;
                    Max=max(Max,heights[mid]*(right-left-1));
                }
                stack.push(i);
            }
        }
        //-----Change 3
        If the stack is not empty, it proves that there is an increasing sequence in it, which means that there is no smaller value on the right than them
        that right=height.size()That's right
        left It's the previous element in the stack
        //while(stack.empty()== false){
        //    int mid=stack.top(); stack.pop();
        //    int left;
        //    int right=heights.size();
        //    if(stack.empty()== false) left=stack.top();
        //    else left=-1;
        //    Max=max(Max,heights[mid]*(right-left-1));
        //}
        return Max;
    }
};