0x00 Preface
Information system security experiment
Experiment 1: implementation and cracking of classical encryption algorithm
1. Realize Caesar encryption and brute force cracking Caesar encryption
2. Select k value and compile Caesar encryption algorithm
3. Write an algorithm to try to brutally crack Caesar encryption
Experiment 2: large prime generation algorithm, the advantages and disadvantages of different prime generation algorithms
1. Using Fermat's small theorem and prime number judgment method to generate large prime numbers
2. The millarabin prime number decision algorithm is used to generate large prime numbers
3. The characteristics of two algorithms are summarized
0x01 implementation and cracking of classical encryption algorithm
1, Realize Caesar encryption
In cryptography, Caesar cipher (English: Caesar cipher), or Caesar encryption, Caesar transform, transform encryption, is the simplest and most well-known encryption technology. It is A replacement encryption technology. All letters in plaintext are shifted backward (or forward) according to A fixed number on the alphabet and replaced with ciphertext. For example, when the offset is 3, all letters A will be replaced with D, B will become E, and so on. This encryption method was named after Caesar in the Roman Republic, who used this method to contact his generals.
Encrypt:
def encrypt():
global result
for word in message:
if word in dic:
num = dic.find(word)
offset = (num + key) % 26
word = dic[offset]
result = result + word
Decrypt:
def decrypt():
global result
for word in message:
if word in dic:
num = dic.find(word)
offset = num - key
if offset < 0:
offset = offset + 26
word = dic[offset]
result = result + word
The_fu11_scr1pt:
dic = "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
result = ''
message = input('Please input the message:')
mode = input('Please input the mode:')
key = input('Please input the key:')
key = int(key)
def encrypt():
global result
for word in message:
if word in dic:
num = dic.find(word)
offset = (num + key) % 26
word = dic[offset]
result = result + word
def decrypt():
global result
for word in message:
if word in dic:
num = dic.find(word)
offset = num - key
if offset < 0:
offset = offset + 26
word = dic[offset]
result = result + word
def main():
if mode == 'encrypt':
encrypt()
if mode == 'decrypt':
decrypt()
print(result)
if __name__ == '__main__':
main()
The operation results are as follows:
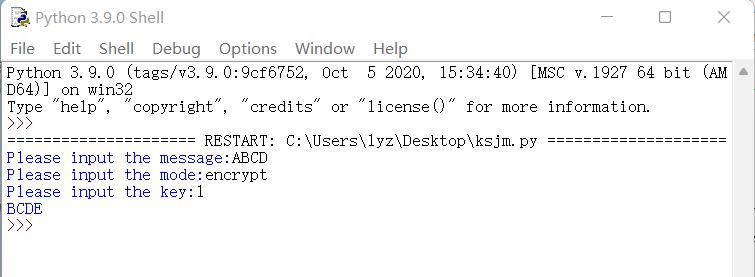
The author wrote here is relatively simple, only considering uppercase letters. If you want to cover lowercase letters or even special characters, you can use the string module provided by python or write according to ascii.
print [chr(i) for i in range(65,91)] #All capital letters print [chr(i) for i in range(97,123)] #All lowercase letters print [chr(i) for i in range(48,58)] #All numbers
import string #Import the string module print string.digits #Output a string containing numbers 0 to 9 print string.letters #A string containing all letters (uppercase or lowercase) print string.lowercase #A string containing all lowercase letters print string.uppercase #A string containing all uppercase letters print string.punctuation #A string containing all punctuation print string.ascii_letters #Same as string.letters
2, Brute force Caesar encryption
dic = "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
message = input('Please input the message:')
def decrypt(key):
global result
result = ''
for word in message:
if word in dic:
num = dic.find(word)
offset = num - key
if offset < 0:
offset = offset + 26
word = dic[offset]
result = result + word
def main():
for key in range(1,27):
decrypt(key)
print('key:' + str(key) + '\t result:' + result)
if __name__ == '__main__':
main()
The operation results are as follows:
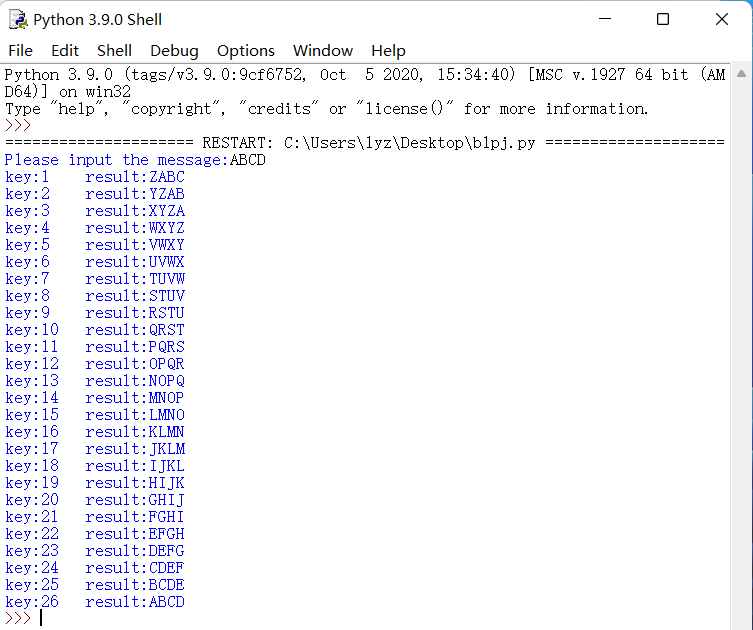
0x02 large prime generation algorithm
1, Using Fermat's small theorem and prime number judgment method to generate large prime numbers
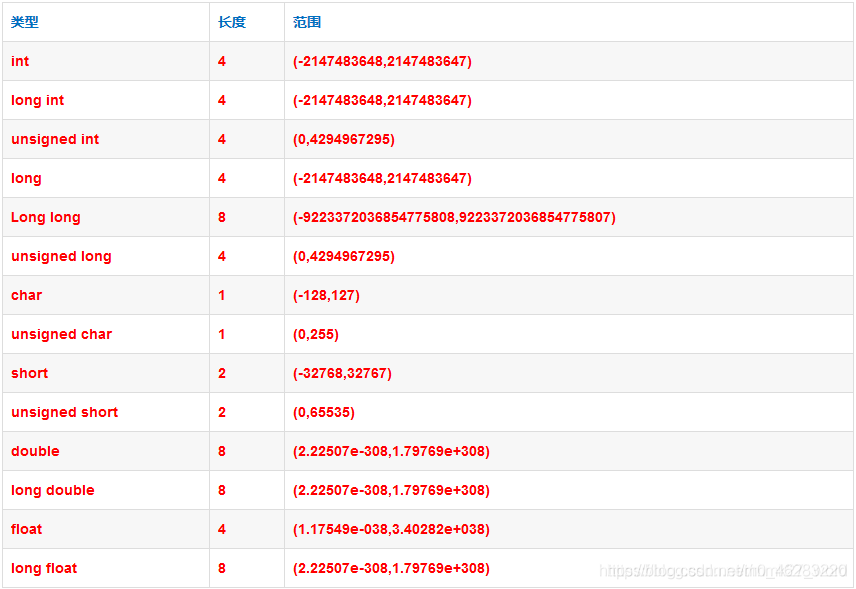
Fermat's little theorem is an important theorem in number theory, which was proposed in 1636. If P is a prime number and the integer a is not a multiple of P, there is a^(p-1) ≡ 1 (mod p).
From the above formula, p = a^(p-1) * p + 1. We make a = p-1 to obtain a larger p value. The algorithm is implemented as follows:
# include<iostream>
# include<math.h>
using namespace std;
int main()
{
long long a,t,p;
cout<<"Please enter an integer:";
cin>>p;
a = p-1;
t = pow(a,a);
p = t*p + 1;
//cout<<"p = "<<p<<endl;
cout<<"The large prime number is:"<<p<<endl;
}
The operation results are as follows:
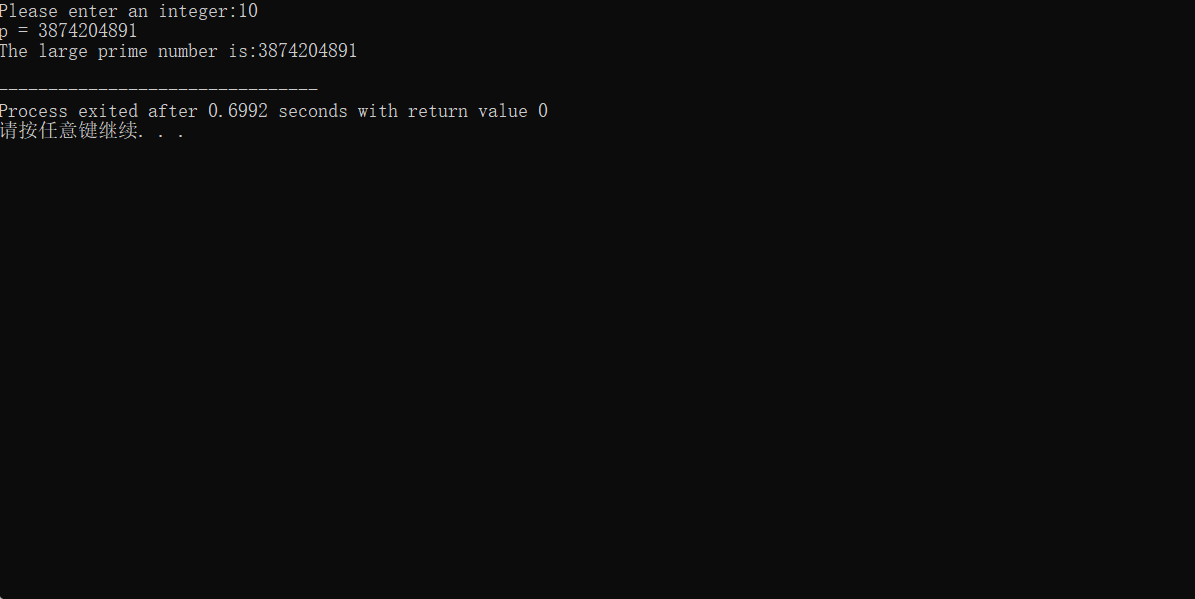
However, when the result is too large to exceed the range of long long, we must use other methods to realize the operation. For example, an array or string is used to represent a value, and then the constructor is used to realize the operation of large numbers.
For the implementation of C + + large integer operation, please refer to the following articles:
https://www.cnblogs.com/yilis/p/10680176.html
https://blog.csdn.net/Ring_k/article/details/80615561
https://www.cnblogs.com/youngforever/articles/3262043.html
2, Using Miller Rabin Prime Number Decision Method to generate large prime numbers
p is a prime number, which must satisfy Fermat's small theorem, but the number satisfying Fermat's small theorem is not necessarily a prime number. Although some numbers satisfy Fermat's theorem, they are not prime numbers. They are called pseudo prime numbers (Carmichael). The number of pseudo prime numbers is infinite. Therefore, if we use Fermat's small theorem to generate large prime numbers, there will be a certain probability of error. What is the probability of this error? How many numbers are pseudo prime numbers in a certain range? This is related to the value of A. When a = 2, 5597 of the first billion positive integers that can satisfy Fermat's theorem and are not prime numbers, that is, the probability of error is 0.011%. Although its error rate is not high, it can not be denied that there are still a certain number of pseudo primes that can not be detected by Fermat's small theorem. Therefore, we need a method to screen out these pseudo primes as much as possible, which is the core part of millarbin algorithm.

Therefore, if we want to judge whether P is a prime number, we can traverse the value of X (0 < x < p) according to the quadratic detection theorem and calculate whether the solutions of x^2 ≡ 1 (mod p) are x = 1 and x = p-1 (trivial square root), that is, if and only if x = 1 or x = p-1, x^2 ≡ 1 (mod p) holds. However, when the value of P is too large, it is impractical to traverse X. Miller Rabin algorithm provides a fast and relatively accurate method.
Although we traverse x to make it mod p, we only need X that can make x^2 ≡ 1 (mod p) true. In turn, let's take out all x that can make x^2 ≡ 1 (mod p) and see whether they are equal to p - 1 or 1. But how can we quickly find these x's that make the equation hold without calculation? Let's take a look at the Fermat sex test just now.
All prime numbers are odd. Any even number can be written in the form of 2^s * t, such as 6 = 2 ^ 1 * 3
a^(p-1) ≡ 1 (mod p) = > A ^ (2 ^ s * t) ≡ 1 (mod p) = > (a ^ t) ^ (2 ^ s) ≡ 1 (mod p), so that a^t = k
(a^t)^(2^s) ≡ 1 (mod p) => k^(2^s) ≡ 1 (mod p) => (k * k * ...... * k)^2 ≡ 1 (mod p) => x^2 ≡ 1 (mod p)
To sum up, traversing x is equivalent to traversing k, and traversing k is equivalent to traversing a (t is a computable constant, and the calculation method is shown below). In fact, millarbin algorithm is to randomly take a certain number of different a to obtain different k, and then continuously detect the square of k (s times) to judge whether it is equal to 1 or p-1. Try a few more k, that is, try a few more a, and the error probability of this algorithm can be reduced to negligible.
Calculation method of t:
Taking 72 as an example, the number of uninterrupted zeros from the lowest point in 72 = 1001000 = 8 * 9 = 2 ^ 3 * 91001000 is 3, so t = 3.
Another example is 28 = 11100 = 4 * 7 = 2 ^ 2 * 7, t = 2.
Fast product:
3 * 7 => 3 * (111) => 3 * (2^0 + 2^1 +2^2) => 3 * (1 + 2 + 4)
Let res=3, res = res + res=3 * 2 = 6 = > res = res + res=3 * 4 = 12
long long Quick_Multiply(int a,int b,int c)
{
long long ans=0,res=a;
while(b)
{
if(b&1) //Is the low order 1
ans=(ans+res)%c;
res=(res+res)%c;
b>>=1; //Move left one bit, i.e. remove the lowest bit
}
return ans;
}
Fast power:
3^5 => 3^(101) => 3^(2^0 + 2^2) => 3^(1 + 4) => 3^1 * 3^4
Let res = 3, res = res * res = 9 (the second digit is 0, so 9 does not participate in the operation) = > res = res * res = 81 = 3 ^ 4
long long Quick_Power(int a,int b,int c)
{
int ans=1,res=a;
while(b)
{
if(b&1)
ans=Quick_Multiply(ans,res,c);
res=Quick_Multiply(res,res,c);
b>>=1;
}
return ans;
}
Miller Rabin test:
bool Miller_Rabin(long long x)
{
long long i,j,k;
long long s=0,t=x-1;
//cout<<t<<endl;
if(x==2) return true;
if(x<2||!(x&1)) return false; //And operation to judge whether the lowest bit of binary x is 1, that is, whether x is an odd number
while(!(t&1))
{
s++;
t>>=1; //Shift operation, delete the lowest bit of n binary
}
for(i=0;i<10&&prime[i]<x;++i)
{
long long a=prime[i];
long long b=Quick_Power(a,t,x);
for(j=1;j<=s;++j)
{
k=Quick_Multiply(b,b,x);
if(k==1&&b!=1&&b!=x-1)
return false;
b=k;
}
if(b!=1) return false;
}
return true;
}
Combined with Fermat's small theorem and Miller Rabin primality test, a large prime number generation code is constructed:
#include<iostream>
#include<math.h>
using namespace std;
typedef long long ll;
int prime[10]={2,3,5,7,11,13,17,19,23,29};
ll Quick_Multiply(ll a,ll b,ll c)
{
ll ans=0,res=a;
while(b)
{
if(b&1)
ans=(ans+res)%c;
res=(res+res)%c;
b>>=1;
}
return ans;
}
ll Quick_Power(ll a,ll b,ll c)
{
ll ans=1,res=a;
while(b)
{
if(b&1)
ans=Quick_Multiply(ans,res,c);
res=Quick_Multiply(res,res,c);
b>>=1;
}
return ans;
}
bool Miller_Rabin(ll x)
{
ll i,j,k;
ll s=0,t=x-1;
//cout<<t<<endl;
if(x==2) return true;
if(x<2||!(x&1)) return false;
while(!(t&1))
{
s++;
t>>=1;
}
for(i=0;i<10&&prime[i]<x;++i)
{
ll a=prime[i];
ll b=Quick_Power(a,t,x);
for(j=1;j<=s;++j)
{
k=Quick_Multiply(b,b,x);
if(k==1&&b!=1&&b!=x-1)
return false;
b=k;
}
if(b!=1) return false;
}
return true;
}
int main()
{
ll x,y,z,flag;
cout<<"Please enter an integer:";
cin>>flag;
while(true)
{
x=flag;
y=x-1;
z=pow(y,y);
x=x*z+1;
cout<<"x = "<<x<<endl; //Check whether it is out of bounds
if(Miller_Rabin(x))
{
cout<<"The large prime number is:"<<x<<endl;
break;
}
else
{
cout<<x<<" is not a prime number,it will add the integer you enter to 1 and try again"<<endl;
flag++;
}
}
return 0;
}
The operation results are as follows:
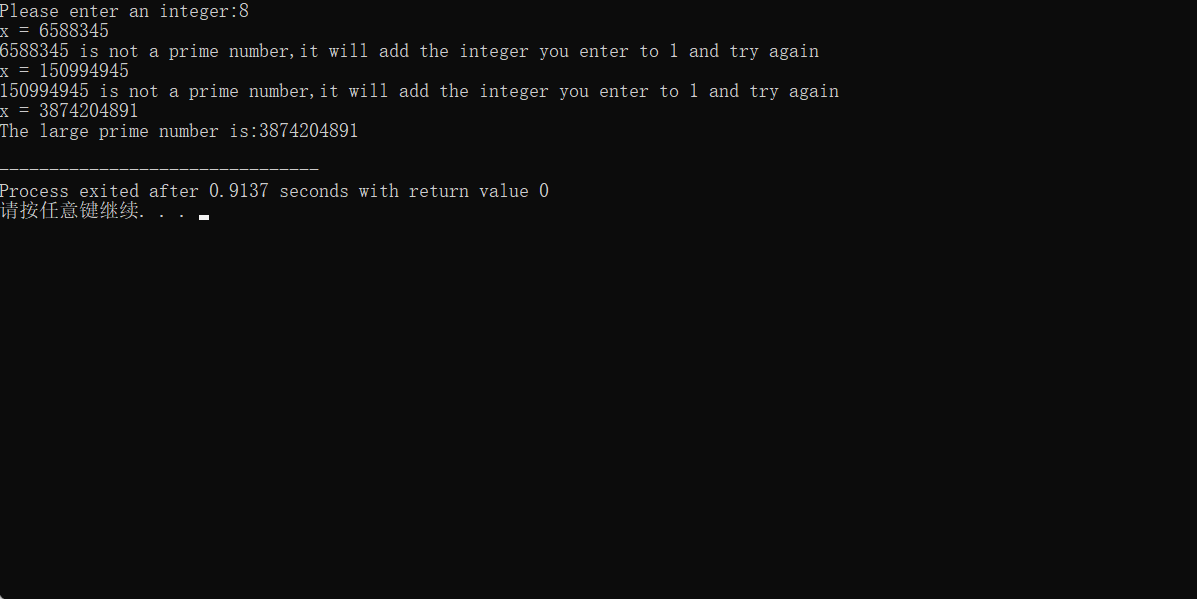
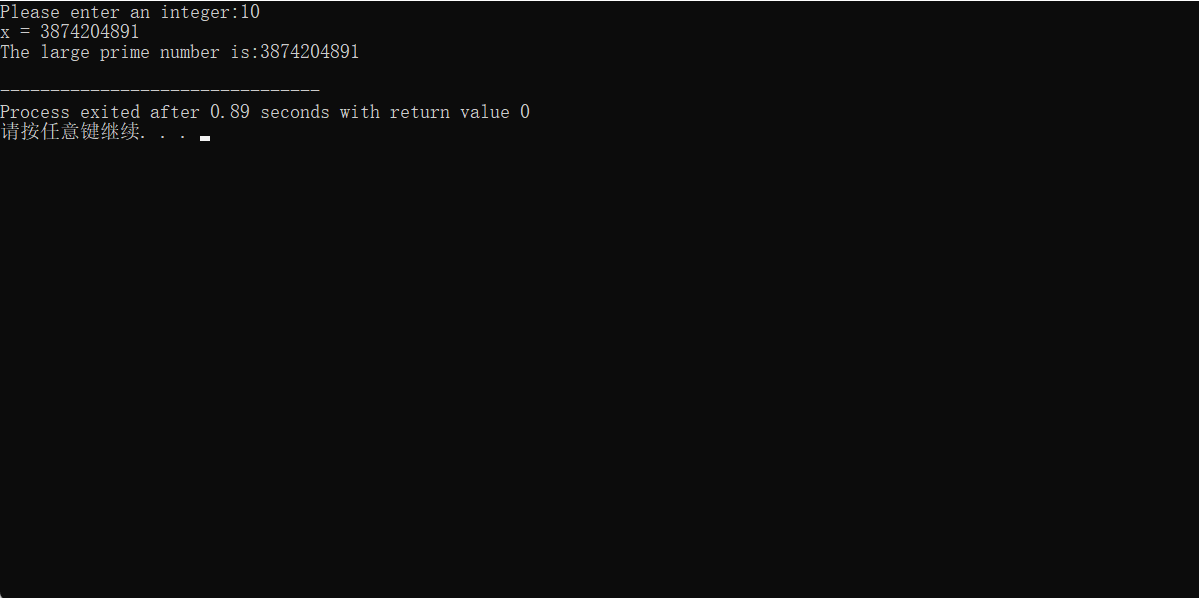
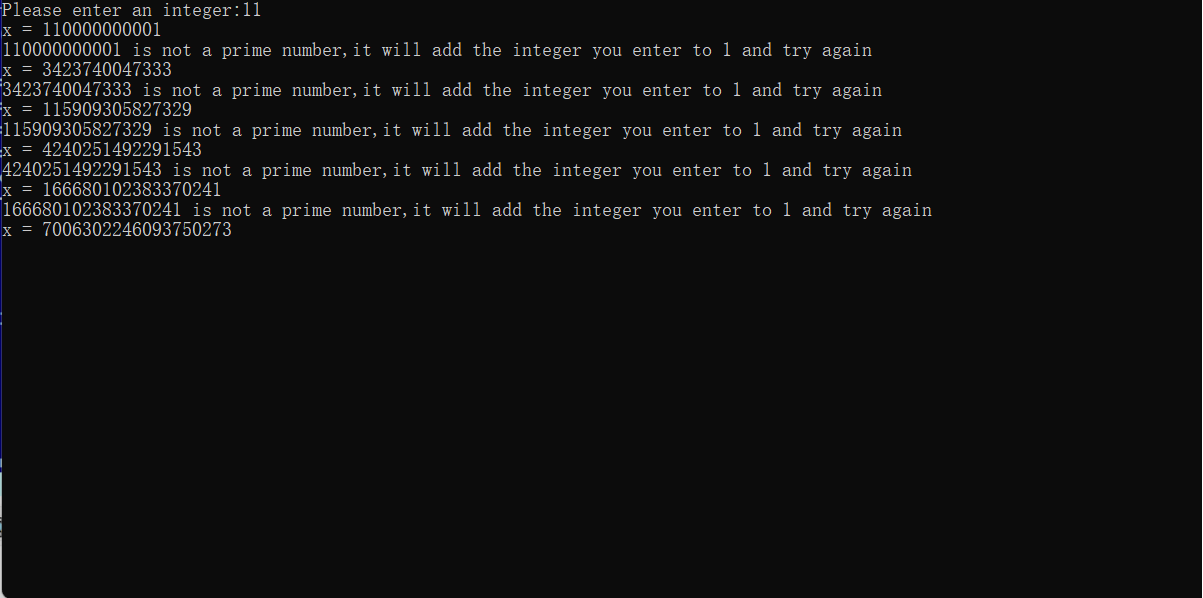
It can be seen that when the input integer is 11, the program runs to x out of bounds and fails to generate prime numbers. Large prime numbers can be found here: Large prime table
0x03 Summary
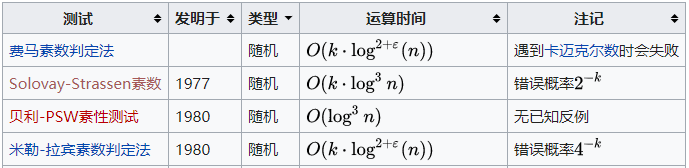
Both Fermat prime number determination and Miller Rabin Prime Number Determination belong to randomness test. This kind of test method is generally faster, but it can not completely prove whether a number is a prime number. In Miller Rabin algorithm, with the increase of the number of successful tests, the probability of composite number will decline exponentially, and the reliability of prime number will be greater and greater (but not completely credible). Once the test fails, it indicates that the number is a certain composite number.
0x04 Reference
https://blog.csdn.net/qq_42146775/article/details/102562329
https://blog.csdn.net/forever_dreams/article/details/82314237
https://blog.csdn.net/holly_Z_P_F/article/details/85197424