preface

After a month, let's try to play a wave of Snake games automatically with the help of Hamilton ring. Let's start happily~

development tool

**Python version: * * 3.6.4

Related modules:

pygame module;

And some python built-in modules.

Environment construction

Install Python and add it to the environment variable. pip can install the relevant modules required.

Principle introduction

Here we mainly talk about how to design algorithms to automatically play Snake games. Let's briefly introduce the definition of Hamiltonian ring (quoted from Wikipedia):

1. Hamiltonian graph is an undirected graph, which was proposed by Sir Hamilton,
2. From the specified starting point to the specified ending point, you pass through all other nodes and only once.
3. In graph theory, it refers to the graph containing Hamiltonian circuit,
4. A closed Hamiltonian path is called a Hamiltonian cycle,
5. A path containing all vertices in a graph is called a Hamiltonian path
6. (English: Hamiltonian path, or Traceable path).
7. Definition of Hamiltonian graph: G=(V,E) is a graph,
8. If a path in G passes through each vertex only once,
9. This path is called Hamiltonian path.
10. If a cycle in G passes through each vertex only once, it is called Hamiltonian cycle.
11. If a graph has a Hamiltonian cycle, it is called a Hamiltonian graph. Finally, if your time is not very tight and you want to improve python quickly, the most important thing is not afraid of hardship. It is recommended that you can price @ 762459510. That's really good. Many people make rapid progress and need you to be not afraid of hardship! You can add it and have a look~

For example, there is a 4 * 4 map:

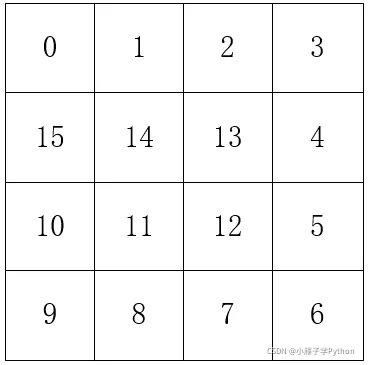
Then the Hamiltonian ring can be (not unique):

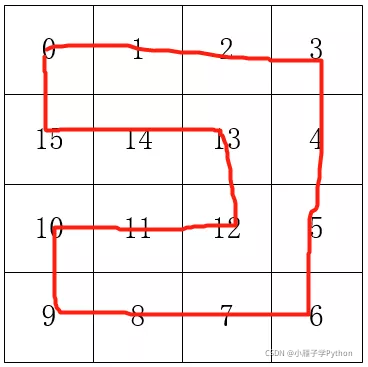
By constructing the Hamiltonian ring, we can easily ensure that the snake will not die because of hitting itself in the process of movement. For example, assuming that lattice 0, 1 and 2 are our greedy snakes, in which 2 is the head of the snake, 0 is the tail of the snake, and the rest are the body of the snake, we can construct the Hamiltonian ring through the following algorithm (Figure source reference [1]):

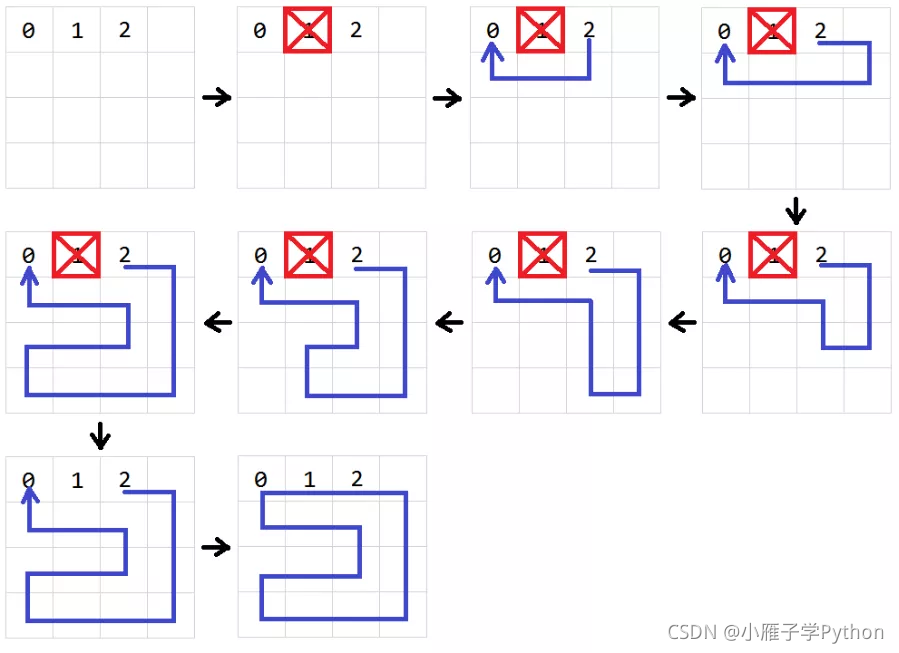
Note that this algorithm is not a general algorithm for finding Hamiltonian rings, so there is a case that Hamiltonian rings cannot be found (in order to improve the probability of finding Hamiltonian rings by the algorithm, we changed the 4025 squares in the original game map to 2020 squares).

Specifically, the code implementation of the algorithm is as follows:

'''check boundary'''
def checkboundary(self, pos):
  if pos[0] < 0 or pos[1] < 0 or pos[0] >= self.num_cols or pos[1] >= self.num_rows:
    return False
  return True
'''the shortest'''
def shortest(self, wall, head, food):
  wait = OrderedDict()
  node, pre = head, (-1, -1)
  wait[node] = pre
  path = {}
  while wait:
    node, pre = wait.popitem(last=False)
    path[node] = pre
    if node == food:
      break
    if pre in path:
      prepre = path[pre]
      direction = (pre[0]-prepre[0], pre[1]-prepre[1])
      if (direction in self.directions) and (direction != self.directions[0]):
        self.directions.remove(direction)
        self.directions.insert(0, direction)
    for direction in self.directions:
      to = (node[0] + direction[0], node[1] + direction[1])
      if not self.checkboundary(to):
        continue
      if to in path or to in wait or to in wall:
        continue
      wait[to] = node
  if node != food:
    return None
  return self.reverse(path, head, food)
'''reverse path'''
def reverse(self, path, head, food):
  if not path: return path
  path_new = {}
  node = food
  while node != head:
    path_new[path[node]] = node
    node = path[node]
  return path_new
'''the longest'''
def longest(self, wall, head, food):
  path = self.shortest(wall, head, food)
  if path is None:
    return None
  node = head
  while node != food:
    if self.extendpath(path, node, wall+[food]):
      node = head
      continue
    node = path[node]
  return path
'''extend path'''
def extendpath(self, path, node, wall):
  next_ = path[node]
  direction_1 = (next_[0]-node[0], next_[1]-node[1])
  if direction_1 in [(0, -1), (0, 1)]:
    directions = [(-1, 0), (1, 0)]
  else:
    directions = [(0, -1), (0, 1)]
  for d in directions:
    src = (node[0]+d[0], node[1]+d[1])
    to = (next_[0]+d[0], next_[1]+d[1])
    if (src == to) or not (self.checkboundary(src) and self.checkboundary(to)):
      continue
    if src in path or src in wall or to in path or to in wall:
      continue
    direction_2 = (to[0]-src[0], to[1]-src[1])
    if direction_1 == direction_2:
      path[node] = src
      path[src] = to
      path[to] = next_
      return True
  return False
'''build a Hamiltonian cycle'''
def buildcircle(self, snake):
  path = self.longest(snake.coords[1: -1], snake.coords[0], snake.coords[-1])
  if (not path) or (len(path) - 1 != self.num_rows * self.num_cols - len(snake.coords)):
    return None
  for i in range(1, len(snake.coords)):
    path[snake.coords[i]] = snake.coords[i-1]
  return path

That is to find the shortest path from snake head to snake tail, and then construct the Hamiltonian ring we need by expanding the path. (some friends may ask, the shortest path has been found, why expand it into a Hamiltonian ring? Note that we are playing greedy snake here, and the goal is to eat the food on the map, rather than keep moving with your tail.) finally, if you are not very nervous about your time and want to improve python quickly, the most important thing is not afraid of hardship, I suggest you can price @ 762459510. That's really good. Many people make rapid progress. You need to be not afraid of hardship! You can add it and have a look~

Because always following the fixed loop is cumbersome and time-consuming, it looks very stupid. For example, according to the algorithm designed above, the greedy snake will move like the following figure:

[external chain picture transfer failed. The source station may have anti-theft chain mechanism. It is recommended to save the picture and upload it directly (IMG uaauqpbp-1634801285542)( https://upload-images.jianshu.io/upload_images/2539976-1ad1f7e4ee289ca0.gif )]

To solve this problem, we can use the following rules to make snakes take some shortcuts (source reference [1]):

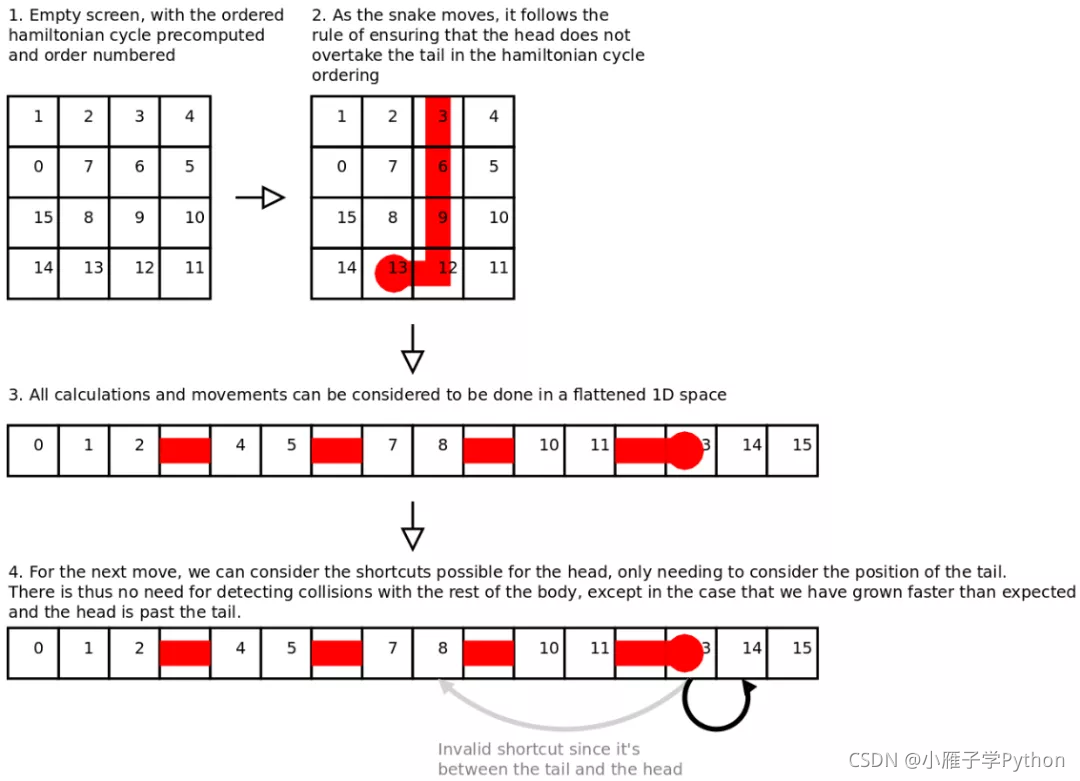
First create an empty matrix as large as the game grid matrix:

world = [[0 for i in range(self.num_cols)] for j in range(self.num_rows)]

Then, according to the previously calculated Hamiltonian ring, the empty matrix is sequentially filled with ordered numbers:

num = 1
node = snake.coords[-1]
world[node[1]][node[0]] = num
node = self.path[node]
while node != snake.coords[-1]:
  num += 1
  world[node[1]][node[0]] = num
  node = self.path[node]

Using these ordered numbers, we can easily find a shortcut to the movement of greedy snakes (in fact, we can approach the randomly generated food on the map as soon as possible without bumping into ourselves, that is, the grid number in the next step is as close to the number of the grid where the food is located as possible):

# obtain shortcut_path
wall = snake.coords
food = food.coord
food_number = world[food[1]][food[0]]
node, pre = wall[0], (-1, -1)
wait = OrderedDict()
wait[node] = pre
path = {}
while wait:
  node, pre = wait.popitem(last=False)
  path[node] = pre
  if node == food:
    break
  node_number = world[node[1]][node[0]]
  neigh = {}
  for direction in self.directions:
    to = (node[0]+direction[0], node[1]+direction[1])
    if not self.checkboundary(to):
      continue
    if to in wait or to in wall or to in path:
      continue
    to_number = world[to[1]][to[0]]
    if to_number > node_number and to_number <= food_number:
      neigh[node_number] = to
  neigh = sorted(neigh.items(), key=itemgetter(0), reverse=True)
  for item in neigh:
    wait[item[1]] = node
if node != food:
  return {}
return self.reverse(path, snake.coords[0], food)

That's all, the complete source code. See the profile of your home page for relevant documents.