Backpack series
- State representation f(i,j)
- aggregate
- All
- Meet the conditions
- attribute
- Maximum
- minimum value
- quantity
- ...
- aggregate
- State calculation
1, 01 Backpack
Features: each item can only be used once (or not)
State calculation: divide the set into selected i and unselected i
1.1 simple writing (two-dimensional)
/**
* f[i][j]Indicates the maximum value when only the first i items are viewed and the total volume is j.
* The answer to be returned is: max(f[n][0~v])
* f[i][j]Recurrence:
* 1. If the ith item is not selected, f[i][j] = f[i-1][j]
* 2. Select the ith item, f[i][j] = f[i-1][j-v[i]] + w[i]// Here is a curve to save the country
* f[0][0] = 0 //When no item is selected, the maximum value is 0
**/
#include<cstdio>
#include<algorithm>
using namespace std;
const int N = 1000 + 10;
int f[N][N];
int w[N], v[N]; //Default initialization is 0
int n, t;
int main() {
scanf("%d%d", &n, &t);
for (int i = 1; i <= n; i++) scanf("%d%d", &v[i], &w[i]);
// The default initialization is 0, so you don't need to start from 0
for (int i = 1; i <= n; i ++) {
for (int j = 0; j <= t; j ++) {
f[i][j] = f[i - 1][j];
// If the current backpack capacity is insufficient, the maximum value of the first i items is the maximum value of the first i-1 items (that is, the statement in the following if is false)
// On the contrary, if the current backpack capacity is sufficient, the maximum value of the ith item is selected or not (that is, the if statement is true)
if (j >= v[i]) f[i][j] = max(f[i][j], f[i-1][j-v[i]] + w[i]);
}
}
printf("%d\n", f[n][t]);
return 0;
}
1.2 after optimization (one dimension + rolling array)
/**
The state f[i][j] defined by us can obtain any legal I and j optimal solutions, but the problem only needs to obtain the final state f[n][m], so the state can be updated only in one-dimensional space. It's like finding the o(1) space of Fibonacci sequence (f[n] = f[n-1] + f[n-2]) and rolling calculation with three variables a, b and c.
In the two-dimensional simple writing method, it can be found that only f[i-1][j] and f[i-1][j-v[i] are used to find f[i][j]. Using the principle of rolling array, the two-dimensional space is transformed into one-dimensional space.
Status f[j] indicates that the backpack capacity is the maximum value of j under the current k items. Ps: since the information of the first dimension of the two-dimensional array (the information of the i-th item) is discarded in the front, the state f[j] array after the end of the cycle is equivalent to f[n][j] in the simple writing method.
Why is the loop here in reverse order?
Answer: f[j] = max(f[j], f[j-v[i]] + w[i]) in the circulatory body; Corresponding to f[i][j] = max(f[i-1][j], f[i-1][j-v[i]] + w[i]). Assuming i=2 and j from 1 to 5, we first find f[1] when i=2, and then use f[1] when i=2 to find f[2], but in fact, we need to use f[1] when i=1 to find f[2]. In other words, the state of the i-1 round used for the positive sequence update f[j] is polluted by the I theory.
**/
#include<cstdio>
#include<algorithm>
using namespace std;
const int N = 1000 + 10;
int f[N], w[N], v[N]; //Default initialization is 0
int n, t;
int main() {
scanf("%d%d", &n, &t);
for (int i = 1; i <= n; i++) scanf("%d%d", &v[i], &w[i]);
for (int i = 1; i <= n; i ++) {
for (int j = t; j >= v[i]; j --) {
f[j] = max(f[j], f[j-v[i]] + w[i]);
}
}
printf("%d\n", f[t]);
return 0;
}
1.3 other issues:
1.3.1 about whether the volume of f[i][j] is exactly j or not exceeding j


2, Complete Backpack
Features: each item can be used unlimited times (there are unlimited)
-
State representation f(i,j)
- Collection: all options that only consider the first i items and the total volume is not greater than j
- Attributes: maximum
-
State calculation
- Collection Division: select 0, 1, 2,... k items according to the ith item.
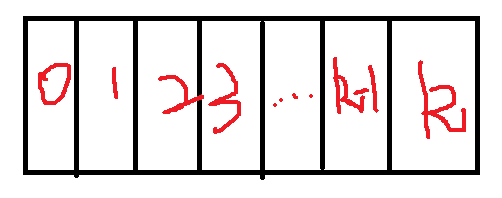
- f[i][j] = max(f[i - 1][j - k * v[i]] + w[i]*k)
2.1 simple writing
#include<cstdio>
#include<algorithm>
using namespace std;
const int N = 1000 + 10;
int f[N][N];
int w[N], v[N];
int n,t;
int main() {
scanf("%d%d", &n, &t);
for (int i = 1; i <= n; i++) scanf("%d%d", &v[i], &w[i]);
for (int i = 1; i <= n; i ++) {
for (int j = 0; j <= t; j ++) {
for (int k = 0; k * v[i] <= j; k ++) {
f[i][j] = max(f[i][j], f[i-1][j - k*v[i]] + k*w[i]);
}
}
}
printf("%d\n", f[n][t]);
return 0;
}
2.2 optimization (two-layer cycle)
It is known from the above that f[i][j] = max(f[i - 1][j - k * v[i]] + w[i]*k), that is, f[i][j] is the maximum value that K class I commodities can achieve when the volume is less than or equal to j.
f [ i ] [ j ] = M a x ( f [ i − 1 ] [ j ] , f [ i − 1 ] [ j − v ] + w , f [ i − 1 ] [ j − 2 v ] + 2 w , f [ i − 1 ] [ j − 3 v ] + 3 w . . . f [ i − 1 ] [ j − k v ] + k w ) f[i][j] = Max(f[i-1][j], f[i-1][j-v] + w, f[i-1][j-2v] + 2w, f[i-1][j-3v] + 3w ... f[i-1][j-kv] + kw) f[i][j]=Max(f[i−1][j],f[i−1][j−v]+w,f[i−1][j−2v]+2w,f[i−1][j−3v]+3w...f[i−1][j−kv]+kw)
f [ i ] [ j − v ] = M a x ( f [ i − 1 ] [ j − v ] , f [ i − 1 ] [ j − 2 v ] + w , f [ i − 1 ] [ j − 3 v ] + 2 w , f [ i − 1 ] [ j − 4 v ] + 3 w ) . . . f [ i − 1 ] [ j − k v ] + ( k − 1 ) w ) f[i][j-v] = Max(f[i-1][j-v], f[i-1][j-2v] + w, f[i-1][j-3v] + 2w, f[i-1][j-4v] + 3w)...f[i-1][j-kv] + (k-1)w) f[i][j−v]=Max(f[i−1][j−v],f[i−1][j−2v]+w,f[i−1][j−3v]+2w,f[i−1][j−4v]+3w)...f[i−1][j−kv]+(k−1)w)
It can be deduced from the above two equations:
f [ i ] [ j ] = M a x ( f [ i − 1 ] [ j ] , f [ i ] [ j − v ] + w ) f[i][j] = Max(f[i-1][j], f[i][j-v] + w) f[i][j]=Max(f[i−1][j],f[i][j−v]+w)
At this time, the state of f[i][j] is independent of the value of k, so the for loop of k can be removed.
#include<cstdio>
#include<algorithm>
using namespace std;
const int N = 1000 + 5;
int f[N][N];
int v[N], w[N];
int n, t;
int main () {
scanf("%d%d", &n, &t);
for (int i = 1; i <= n; i ++) scanf("%d%d", &v[i], &w[i]);
for (int i = 1; i <= n; i ++) {
for (int j = 0; j <= t; j ++) {
f[i][j] = f[i - 1][j];
if (j >= v[i]) f[i][j] = max(f[i][j], f[i][j - v[i]] + w[i]);
}
}
printf("%d\n", f[n][t]);
return 0;
}
2.3 optimization (two-layer cycle + one-dimensional state)
After 2.3 optimization, there are only two layers of loops left in the program, and the value of f[i][j] is derived from f[i-1] [...], so we can use the idea of rolling array and follow the principle of equivalent substitution to change two dimensions into one dimension.
#include<cstdio>
#include<algorithm>
using namespace std;
const int N = 1000 + 10;
int f[N];
int v[N], w[N];
int n, t;
int main () {
scanf("%d%d", &n, &t);
for (int i = 1; i <= n; i ++) scanf("%d%d", &v[i], &w[i]);
for (int i = 1; i <= n; i ++) {
for (int j = v[i]; j <= t; j++) {
f[j] = max(f[j], f[j - v[i]] + w[i]);
}
}
printf("%d\n", f[t]);
return 0;
}
After optimization, it can be found that the code difference between 01 knapsack and complete knapsack optimization is that the order of the second layer loop (traversal volume) j is different
- 01 knapsack: the state of layer i needs to be calculated by layer i-1. In order to avoid contamination of layer i-1 data, j adopt reverse order.
- Complete knapsack: the state of layer i needs to be calculated by layer i, so j takes positive order.
3, Multiple Backpack
Features: the number of each item is limited, neither only one nor infinite.
-
State representation f(i,j)
- Collection: all options that only consider the first i items and the total volume is not greater than j
- Attributes: maximum
-
State calculation
- Collection Division: select 0, 1, 2,... k items according to the ith item.

- f[i][j] = max(f[i - 1][j - k * v[i]] + w[i]*k)
3.1 simple writing
#include<cstdio>
#include<algorithm>
using namespace std;
const int N = 100 + 10;
int f[N][N];
int v[N], w[N], s[N];
int n, t;
int main () {
scanf("%d%d", &n, &t);
for (int i = 1; i <= n; i ++) scanf("%d%d%d", &v[i], &w[i], &s[i]);
for (int i = 1; i <= n; i++) {
for (int j = 0; j <= t; j++) {
for (int k = 0; k * v[i] <= j && k <= s[i]; k++) {
f[i][j] = max(f[i][j], f[i - 1][j - k*v[i]] + k * w[i]);
}
}
}
printf("%d\n", f[n][t]);
return 0;
}
3.3 optimization (one-dimensional state)
#include<cstdio>
#include<algorithm>
using namespace std;
const int N = 100 + 10;
int f[N], w[N], v[N], s[N];
int n, t;
int main()
{
scanf("%d%d", &n, &t);
for (int i = 1; i <= n; i ++) scanf("%d%d%d", &v[i], &w[i], &s[i]);
for (int i = 1; i <= n; i ++)
for (int j = t; j >= 0; j --)
for (int k = 0; k <= s[i] && j >= k * v[i]; k ++)
f[j] = max(f[j], f[j - k*v[i]] + k * w[i]);
printf("%d\n", f[t]);
return 0;
}
3.2 optimization (binary – > 01)
Any positive integer can be expressed in binary, that is, it can be expressed in 2 0 − 2 n 2^{0} - 2^{n} 20 − 2n is represented by the sum of one or more of them.
1111b //The decimal system is 15 = 8 (2 ^ 3) + 4 (2 ^ 2) + 2 (2 ^ 1) + 1 (2 ^ 0)
xxxxb //x is 0 or 1, and any combination of 01 forms a binary with 4 bits not all 0. The decimal system obtained from this binary must be less than or equal to 15, and can be obtained by adding any elements of {8, 4, 2, 1}.
// In this way, we can divide item i into multiple items in binary form.
// For example, if the item i has 15 pieces, it can be split into
// Item a (equivalent to 8 items i), item B (equivalent to 4 items i), item C (equivalent to 2 items i), item D (equivalent to 1 item i)
// In this case, according to the rules of 01 backpack, if each item is selected or not, 0 ~ 15 items i can be represented by item a, item b, item c and item d
// Then, we use the above method to split each commodity. The sum of several split commodities is equivalent to the original commodity i, then it is transformed into the 01 knapsack problem.
// It's actually trading space for time.
#include<cstdio>
#include<algorithm>
using namespace std;
const int N = 11000 + 100;
int f[N], v[N], w[N];
int n, t;
int main () {
scanf("%d%d", &n, &t);
int cnt = 1;
for (int i = 1; i <= n; i ++) {
int a, b, s;
scanf("%d%d%d", &a, &b, &s);
// Split goods
for (int j = 1; j <= s; j <<= 1) {
v[cnt] = j * a;
w[cnt] = j * b;
cnt ++;
s -= j;
}
if (s > 0) {
v[cnt] = s * a;
w[cnt] = s * b;
cnt ++;
}
}
// 01 Backpack
for (int i = 1; i < cnt; i ++)
for (int j = t; j >= v[i]; j --)
f[j] = max(f[j], f[j - v[i]] + w[i]);
printf("%d\n", f[t]);
return 0;
}
4, Group Backpack
Features: only one item can be selected in each group
-
State representation f(i,j)
- Collection: all selection methods that only select from the first i group of items and the total volume is not greater than j
- Attribute: value Max
-
State calculation
- Collection Division: for group i items, it is divided according to no selection, No. 1, No. 1,... k.

- f[i][j] = max(f[i - 1][j - k * v[i]] + w[i]*k)
4.1 simple writing
#include<cstdio>
#include<algorithm>
using namespace std;
const int N = 100 + 10;
int f[N][N], v[N][N], w[N][N], s[N];
int n, t;
int main () {
scanf("%d%d", &n, &t);
for (int i = 1; i <= n; i ++) {
scanf("%d", &s[i]);
for (int j = 1; j <= s[i]; j ++) {
scanf("%d%d", &v[i][j], &w[i][j]);
}
}
for (int i = 1; i <= n; i ++) {
for (int j = 0; j <= t; j ++) {
f[i][j] = f[i - 1][j]; //Note that it is outside the third loop, because if there is an update f[i][j] in the third loop, it will be overwritten by this sentence
for (int k = 1; k <= s[i]; k ++) {
if (j >= v[i][k]) f[i][j] = max(f[i][j], f[i - 1][j - v[i][k]] + w[i][k]);
}
}
}
printf("%d\n", f[n][t]);
return 0;
}
4.2 optimization (one-dimensional array)
Follow the example of 01 knapsack optimization
#include<cstdio>
#include<algorithm>
using namespace std;
const int N = 100 + 10;
int f[N], v[N][N], w[N][N], s[N];
int n, t;
int main () {
scanf("%d%d", &n, &t);
for (int i = 1; i <= n; i ++) {
scanf("%d", &s[i]);
for (int j = 1; j <= s[i]; j ++) {
scanf("%d%d", &v[i][j], &w[i][j]);
}
}
for (int i = 1; i <= n; i ++) {
for (int j = t; j >= 0; j --) {
for (int k = 1; k <= s[i]; k ++) {
if (j >= v[i][k]) f[j] = max(f[j], f[j - v[i][k]] + w[i][k]);
}
}
}
printf("%d\n", f[t]);
return 0;
}
experience
Why do subscripts in DP generally start with 1?
If i-1 is involved in the transfer equation, generally let the subscript start from 1, so as to avoid the cross-border problem
Dynamic programming problem involving two strings
Generally, i and J can be used to represent the first i letter of the first string and the first j letter of the second string.