230. The K-th smallest element in the binary search tree

One question per day on October 17, 2021

Title Description

Given the root node root of a binary search tree and an integer k, please design an algorithm to find the K smallest element (counting from 1).

Example 1:

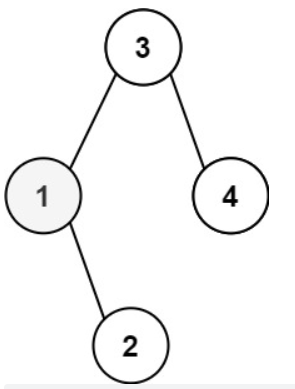
Input: root = [3,1,4,null,2], k = 1
Output: 1

Example 2:

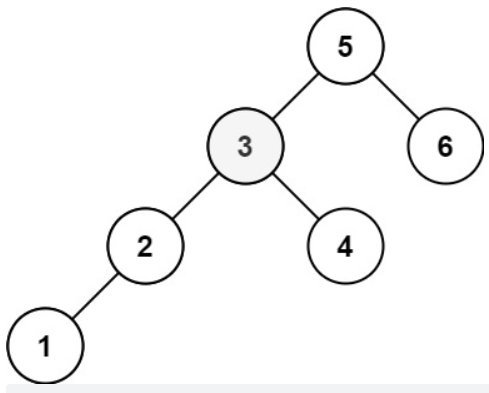
Input: root = [5,3,6,2,4,null,null,1], k = 3
Output: 3

Tips:

The number of nodes in the tree is n.
1 <= k <= n <= 10^4
0 <= Node.val <= 10^4

Advanced: if the binary search tree is often modified (insert / delete operations) and you need to frequently find the k-th smallest value, how will you optimize the algorithm?

Source: LeetCode
Link: https://leetcode-cn.com/problems/kth-smallest-element-in-a-bst
The copyright belongs to Lingkou network. For commercial reprint, please contact the official authorization, and for non-commercial reprint, please indicate the source.

thinking

Because it is a binary search tree, the middle order traversal is arranged from small to large, so the middle order traversal is OK

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    int k;
    TreeNode t = null;
    public int kthSmallest(TreeNode root, int k) {
        //The k-th is the k-th from small to large
        //Is the k-th node traversed in the middle order
        this.k = k;
        inorder(root);
        return t.val;
    }

    public void inorder(TreeNode node){
        if(node == null)
            return;
        if(t != null)
            return;
        inorder(node.left);
        if(--k == 0)
            t = node;
        inorder(node.right);
    }
}

Iterative writing

class Solution {
    public int kthSmallest(TreeNode root, int k) {
        //Write an iterative writing method of medium order traversal
        Stack<TreeNode> stack = new Stack<>();
        
        while(root != null || !stack.isEmpty()){
            while(root != null){
                stack.push(root);
                root = root.left;
            }
            root = stack.pop();
            if(--k == 0)
                return root.val;
            root = root.right;
        }
        return root.val;
    }
}

476. Complement of numbers

One question per day on October 18, 2021

Title Description

The complement of the integer can be obtained by inverting the binary representation of the integer (0 to 1, 1 to 0) and converting it to decimal representation.

For example, the binary representation of integer 5 is "101", which is reversed to get "010", and then turned back to the decimal representation to get complement 2.

Give you an integer num and output its complement.

Example 1:

Input: num = 5
Output: 2
Explanation: the binary representation of 5 is 101 (without leading zero), and its complement is 010. So you need to output 2.

Example 2:

Input: num = 1
Output: 0
Explanation: the binary representation of 1 is 1 (without leading zero), and its complement is 0. So you need to output 0.

Tips:

1 <= num < 2^31

Source: LeetCode
Link: https://leetcode-cn.com/problems/number-complement
The copyright belongs to Lingkou network. For commercial reprint, please contact the official authorization, and for non-commercial reprint, please indicate the source.

thinking

First find out how many digits this number has, and then negate each digit

class Solution {
    public int findComplement(int num) {
        //First find out how many people there are, and then take the opposite one by one
        int n = 0;
        while((1 << n) < num){
            n++;
            if(n == 31)
                break;
        }

        int res = 0;
        for(int i = 1; i <= n; i++){
            res = (res << 1) + (((num >> (n - i)) & 1) ^ 1);
        }
        return res;
    }
}

The reverse operation here can be the exclusive or of num and mask
mask is num, and all bits are 1, which can also achieve the effect. Because of this XOR, the original 0 will become 1, and the original 1 will become 0
In sister Sanye's method, first operate lowbit, that is, subtract one position at a time to find the highest 1. Assuming that it is x, then x-1 is that all bits except the highest are 1; Then you can use the XOR method, or you can use the inverse and then the sum method like sister Sanye

class Solution {
    public int findComplement(int num) {
        int x = 0;
        for(int i = num; i != 0; i -= i & (-i))
            x = i;
        //Take inverse and
        return (x - 1) & ~num;
        //return (x - 1) ^ (num - x);
    }
}

211. Add and search words - data structure design

One question per day on October 19, 2021

Title Description

Please design a data structure that supports adding new words and finding whether the string matches any previously added string.

Implement the dictionary class WordDictionary:

WordDictionary() initializes the dictionary object
void addWord(word) adds word to the data structure, which can then be matched
bool search(word) returns true if there is a string matching word in the data structure; Otherwise, false is returned. Word may contain some '.', and each. Can represent any letter.

Example:

Input:
["WordDictionary","addWord","addWord","addWord","search","search","search","search"]
[[],["bad"],["dad"],["mad"],["pad"],["bad"],[".ad"],["b..."]]
Output:
[null,null,null,null,false,true,true,true]
Explanation:
WordDictionary wordDictionary = new WordDictionary();
wordDictionary.addWord("bad");
wordDictionary.addWord("dad");
wordDictionary.addWord("mad");
wordDictionary.search("pad"); // return False
wordDictionary.search("bad"); // return True
wordDictionary.search(".ad"); // return True
wordDictionary.search("b..."); // return True

Tips:

1 <= word.length <= 500
word in addWord consists of lowercase English letters
word in search consists of '.' or lowercase English letters
addWord and search can be called up to 50000 times

Source: LeetCode
Link: https://leetcode-cn.com/problems/design-add-and-search-words-data-structure
The copyright belongs to Lingkou network. For commercial reprint, please contact the official authorization, and for non-commercial reprint, please indicate the source.

thinking

Dictionary tree plus depth first search, because there is a little

class WordDictionary {
    //Write it yourself
    private boolean isEnd;
    private WordDictionary[] next;
    public WordDictionary() {
        isEnd = false;
        next = new WordDictionary[26];
    }
    
    public void addWord(String word) {
        WordDictionary wd = this;
        int l = word.length();
        for(int i = 0; i < l; i++){
            int t = word.charAt(i) - 'a';
            if(wd.next[t] == null)
                wd.next[t] = new WordDictionary(); 
            wd = wd.next[t];
        }
        wd.isEnd = true;
    }
    
    public boolean search(String word) {
        //Think about how to deal with it
        WordDictionary wd = this;
        int l = word.length();
        return dfs(wd, word, 0);
    }

    public boolean dfs(WordDictionary wd, String word, int idx){
        if(wd == null)
            return false;
        if(idx == word.length() && wd.isEnd)
            return true;
        if(idx == word.length())
            return false;
        char c = word.charAt(idx);
        if(c != '.'){
            if(wd.next[c - 'a'] == null)
                return false;
            else
                return dfs(wd.next[c - 'a'], word, idx + 1);
        }else{
            for(int i = 0; i < 26; i++){
                if(dfs(wd.next[i], word, idx + 1))
                    return true;
            }
            return false;
        }
    }
}

/**
 * Your WordDictionary object will be instantiated and called as such:
 * WordDictionary obj = new WordDictionary();
 * obj.addWord(word);
 * boolean param_2 = obj.search(word);
 */