subject

Problem solving

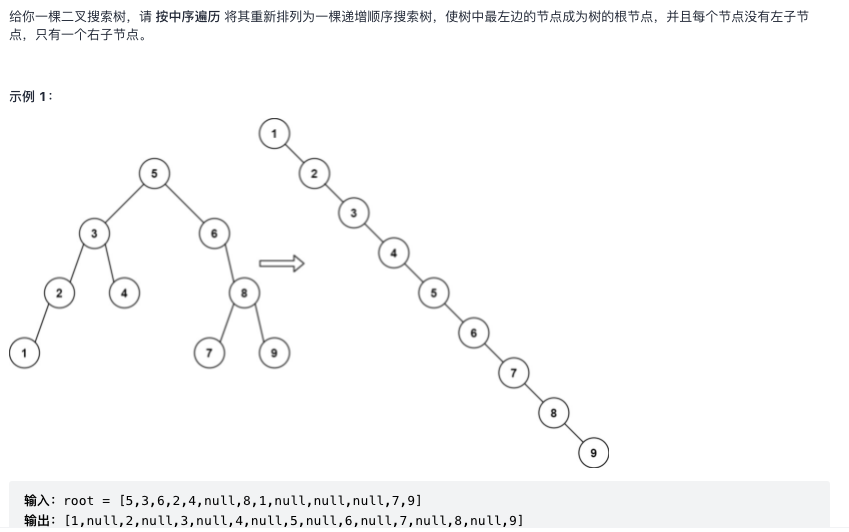
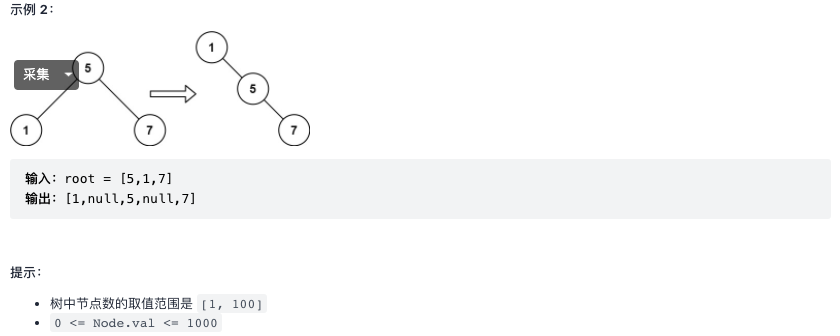
The increasing order of binary search tree is the order of middle order traversal.

LeetCode426 transforms binary search tree into sorted two-way linked list & sword finger Offer 36 binary search tree and two-way linked list The simple version of question 426 needs to construct a two-way circular linked list. This question is a one-way linked list, which is equivalent to that left does not point to the precursor node, but directly points to null, and the last step connected end to end does not need to be used.

Specific ideas are not repeated. Direct directions to 426 questions, and some points for attention are marked out!

In fact, there are several problems that convert binary trees into linked lists, which are essentially middle order / pre order / post order traversal.

1. You can put the nodes into an array in order, and finally modify the left and right pointers
2. You can also modify in situ, but you should pay special attention to when the left pointer and right pointer can be modified: for example, the recursive writing method of preorder traversal. If you point root.right to the left subtree when processing the root node of the left subtree of root, the records of the right subtree will be lost( LeetCode114 binary tree expanded into linked list ). Another example of this problem: when processing the root node, the left subtree has been processed, and the left pointer can be set to null, but if the visit function is written as follows, a ring will appear:

// javascript
const visit = (cur) => {
	if (head === null) {
    	head = cur;
 	}
    if (tail !== null) {
    	tail.left = null;  // Wait until the next node is added to change the left of the tail
		tail.right = cur;
    }
	tail = cur;
};

[2,1,4,null,null,3]
The last node is node 4. There is no node after node 4, so it is left The pointer has no chance to be set to null
 So node 4 left The pointer always points to node 3. The successor nodes of node 3 are node 4 and node 3 right Point to node 4
 So there is a ring

Because the processing flow of different problem-solving ideas is different, we can't draw a conclusion in general. We still need to take the diagram to analyze it and knock the code again. After typing the code, we can check it with the diagram.

In the visit function, there are statements to judge whether the head and tail are null. The official uses the common method of linked list: setting dummy nodes can save the discussion of boundary conditions.

Solution 1: recursion

// javascript
var increasingBST = function(root) {
    const dfs = (root) => {
        if (root === null) return;
        dfs(root.left);
        visit(root);
        dfs(root.right);
    };
    const visit = (cur) => {
        if (head === null) {
            head = cur;
        }
        if (tail !== null) {
            tail.right = cur;
            cur.left = null;
        }
        tail = cur;
    };
    let head = null, tail = null;
    dfs(root);
    return head;
};

Solution 2: stack

// javascript
var increasingBST = function(root) {
    const visit = (cur) => {
        if (head === null) {
            head = cur;
        }
        if (tail !== null) {
            tail.right = cur;
            cur.left = null;
        }
        tail = cur;
    };
    let head = null, tail = null;
    const stk = new Array();
    while (root !== null || stk.length > 0) {
        while (root !== null) {
            stk.push(root);
            root = root.left;
        }
        root = stk.pop();
        visit(root);
        root = root.right;
    }
    return head;
};

Solution 3: order traversal in Morris

// javascript
var increasingBST = function(root) {
    const visit = (cur) => {
        if (head === null) {
            head = cur;
        }
        if (tail !== null) {
            tail.right = cur;
            cur.left = null;
        }
        tail = cur;
    };
    let head = null, tail = null;
    while (root !== null) {
        if (root.left !== null) {
            let predecessor = root.left;
            while (predecessor.right !== null && predecessor.right !== root) {
                predecessor = predecessor.right;
            }
            if (predecessor.right === null) {
                predecessor.right = root;
                root = root.left;
            } else if (predecessor.right === root) {
            	// Emphasize the order again!
                predecessor.right = null;
                visit(root);
                root = root.right;
            }
        } else {
            visit(root);
            root = root.right;
        }
    }
    return head;
};