About boring chatter
When looking at the basic algorithm course, President Y called greed the most difficult algorithm. After listening to it, I felt good. I can do it by feeling!
However, I opened the book and was beaten by reality. The child is too naive. Greed is never difficult in what it does. You are lucky to guess right. It's very good. If you're not lucky to guess wrong, you really don't know where it's wrong.
To sum up, greed depends on feeling and proof depends on talent. Next, let's look at the problem of greed. How difficult is it...

Sunscreen

Original title link:

https://www.acwing.com/problem/content/112/

Main idea of the title:
There are C cows sunbathing, and the ith cow needs sunlight between minSPF[i] and maxSPF[i].

Every cow must wear sunscreen before sunbathing. There are L kinds of sunscreen. After applying the I kind of sunscreen, the sunlight intensity received by the body will stabilize to SPF[i]. There are cover[i] bottles of the I kind of sunscreen.

Ask how many cows can be sunbathed at most.

Input format
On the first line, enter the integers C and L.

In the next line C, input the minSPF and maxSPF values of a cow in order, that is, input minSPF[i] and maxSPF[i] in line I.

In the next L line, input SPF and cover values of a sunscreen in order, that is, input SPF[i] and cover[i] in line I.

The data in each row is separated by spaces.

Output format
Output an integer representing the maximum number of cows that can sunbathe.

Data range
1≤C,L≤2500,
1≤minSPF≤maxSPF≤1000,
1≤SPF≤1000

Input example:
3 2
3 10
2 5
1 5
6 2
4 1
Output example:
2

Title Meaning

That is to say, give you c intervals and l numbers, and ask you how many intervals this L number can contain at most

Problem solving ideas

First, by feeling. Sort the left end point of the interval from small to large, and then sort the L points from small to large. If the points are within the interval, ans + +;
Then, start the test!
WA
So why?
Let's prove our approach. First of all, for point x < y, this is certain, no problem;
Then, for the interval min [i] < min [J], there is no problem, but what about Max [i] < min [J]? Not necessarily! How does this affect the answer?

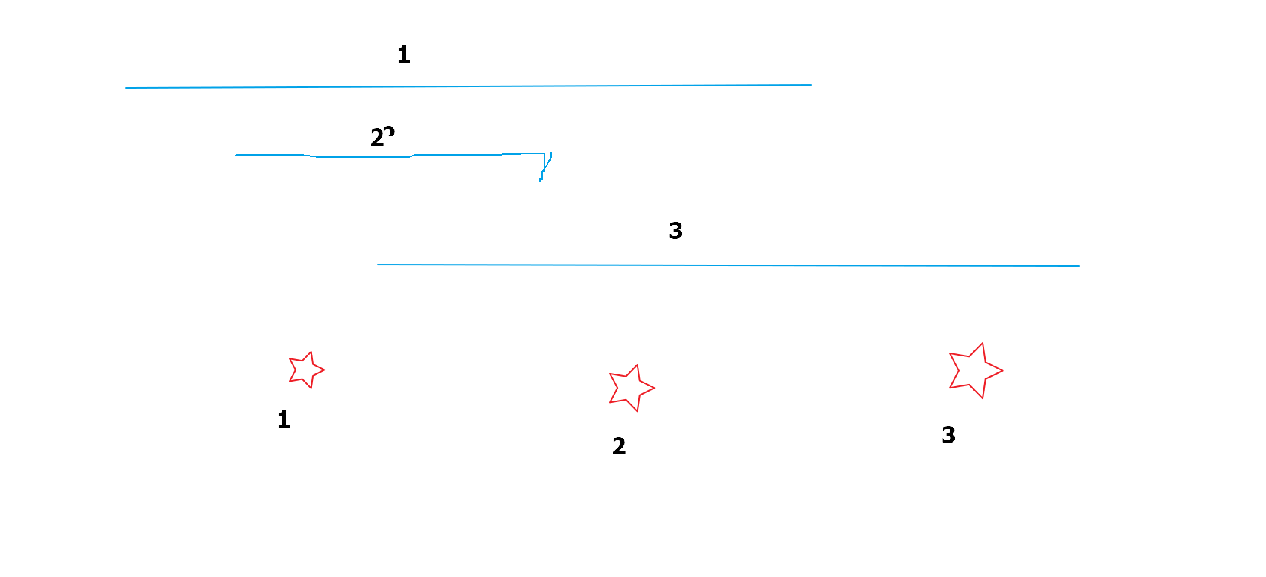
I'm a little ugly. Hahaha, I'll make do with it.
Red stars represent points and blue represents intervals. We can see that if we follow the idea just now, all three stars can correspond to a blue interval, our practice can only correspond to two stars.
So, how to improve it?
Since we can't grow from small to large from the left endpoint, what about the right endpoint?
If you sort from small to large from the right endpoint, this situation will be solved. Then, start typing the code!

AC code

#include<iostream>
#include<algorithm>
using namespace std;

struct sp{
    int minn,maxx;
    bool A=0;
}spf[2510];

struct sp2{
    int spfi,cover;
}spff[2510];

bool cmp1(sp x,sp y){
    if(x.maxx!=y.maxx) return x.maxx<y.maxx;
    else return x.minn<y.minn;
}

bool cmp2(sp2 x,sp2 y){
    if(x.spfi!=y.spfi) return x.spfi<y.spfi;
    else return x.cover<y.cover;
}

int main(){
   int c,l;
   cin>>c>>l;
   
   for(int i=0;i<c;i++){
       cin>>spf[i].minn>>spf[i].maxx;
       if(spf[i].minn>spf[i].maxx) swap(spf[i].minn,spf[i].maxx);
       
   }
   sort(spf,spf+c,cmp1);
   
   for(int i=0;i<l;i++) cin>>spff[i].spfi>>spff[i].cover;
   sort(spff,spff+l,cmp2);
   
   int ans=0;
   for(int j=0;j<l;j++){
       int n=spff[j].cover;
       int m=spff[j].spfi;
      
      for(int i=0;i<c;i++){
          if(spf[i].A==1) continue;
          if(spf[i].minn<=m&&m<=spf[i].maxx){ans++;n--;spf[i].A=1;}
          if(n==0) break;
         // if(spf[i].minn>m) break;
      }
   }
   
 cout<<ans;
 return 0;   
}

Corral reservation

Next is the second question!

Original title link:

https://www.acwing.com/problem/content/113/

Title Description:
There are N cattle grazing in the corral.

Each corral can only be provided for one cow at a time, so multiple corrals may be required.

Given N cows and the time A when each cow starts to graze and the time B when it ends to graze, each cow will graze all the time during [A,B].

When there is an intersection (including the end point) between the grazing areas of two cattle, the two cattle cannot be arranged to graze in the same corral.

Find the minimum number of corrals needed and the corral scheme corresponding to each cow.

Input format
Line 1: enter an integer N.

Line 2... N+1: in line i+1, enter the starting grazing time A and ending grazing time B of the ith cow, separated by A space.

Output format
Line 1: enter an integer representing the minimum number of corrals required.

Line 2... N+1: in line i+1, enter the corral number to which the ith cow is arranged. The number is a continuous integer starting from 1, as long as the scheme is legal.

Data range
1≤N≤50000,
1≤A,B≤1000000

Input example:
5
1 10
2 4
3 6
5 8
4 7
Output example:
4
1
2
3
2
4

General idea of the topic

We have N intervals. We divide all non intersecting intervals into a group. How many groups can we divide at least?

Problem solving ideas

Sort all intervals from small to large, and then traverse them in turn. If the current interval intersects the previous interval, a new group will be created. If there is no intersection, add this interval to the previous interval, and then update the end value of the interval. Here, we need a priority queue to maintain our minimum heap

AC code

#include<iostream>
#include<algorithm>
#include<vector>
#include<cstring>
#include<queue>
using namespace std;

typedef pair<int,int> PII;
const int N=50550;
pair<PII,int> cows[N];
int ans[N];

int main(){
    int n;
    cin>>n;
    for(int i=0;i<n;i++){
        cin>>cows[i].first.first>>cows[i].first.second;
        cows[i].second=i;
    }
    
    sort(cows,cows+n);
    priority_queue<PII,vector<PII>,greater<PII> > head;
    //greater sorts from small to large, less sorts from large to small
    
    for(int i=0;i<n;i++){
        auto cow=cows[i].first;
        if(head.empty()||head.top().first>=cow.first){
            PII stall={cow.second,head.size()+1};
            head.push(stall);
            ans[cows[i].second]=stall.second;
        }else{
            auto stall=head.top();
            head.pop();
            stall.first=cow.second;
            ans[cows[i].second]=stall.second;
            head.push(stall);
        }
    }
    
    cout<<head.size()<<endl;
    for(int i=0;i<n;i++) cout<<ans[i]<<endl;
    return 0;
}

The difficulty here is actually about priority_ A series of operations of queue. After doing this problem, I also learned some interesting writing methods.

Keep going!

Radar equipment

Original title link:

https://www.acwing.com/problem/content/114/

Title Description
Suppose the coast is an infinite straight line, the land is on one side of the coast and the ocean is on the other side.

Each island is located at a point on the ocean side.

All radar devices are located on the coastline, and the radar monitoring range is d. when the distance between the island and a radar does not exceed D, the island can be covered by radar.

We use the Cartesian coordinate system to define the coastline as the x-axis, with the sea side above the x-axis and the land side below the x-axis.

Now, the specific coordinates of each island and the detection range of radar are given. Please find out the minimum number of radars required to make all islands covered by radar.

Input format
In the first line, enter two integers n and d, representing the number of islands and radar detection range respectively.

Next, enter two integers in n lines, representing the x and y axis coordinates of the island.

The same row of data is separated by spaces.

Output format
Output an integer representing the minimum number of radars required. If there is no solution, the required number is output − 1.

Data range
1≤n≤1000,
−1000≤x,y≤1000

Input example:
3 2
1 2
-3 1
2 1
Output example:
2

General idea of the topic

In Cartesian coordinates, we give N points, and then give the scanning range of N points. How many points intersect on the X axis in all the scanning ranges of N points?

Problem solving ideas

Through the triangle theorem, we can calculate the interval formed by each point on the X-axis. At the same time, if there is one that cannot form an interval on the X-axis, we can output - 1. Then we sort the right end from small to large. If the latter left end is less than the right end, it is overlapping; If not, ans + +, update the right end and continue to traverse,

AC code

#include<iostream>
#include<queue>
#include<vector>
#include<math.h>
#include<algorithm>
using namespace std;

typedef pair<double,double> PII;
const int N=1100;
PII ld[N];

bool cmp(PII x,PII y){
    if(x.second!=y.second) return x.second<y.second;
    else return x.first<y.first;
}

int main(){
    
    int n,d;
    cin>>n>>d;
    bool A=0;
    for(int i=0;i<n;i++){
        int a,b;
        cin>>a>>b;
        double c=sqrt(d*d-b*b);
        if(b>d) A=1;
        ld[i].first=a-c,ld[i].second=a+c;
        if(ld[i].first==0&&ld[i].second==0) ld[i].first=ld[i].second=a;
        
        //cout<<c<<" "<<ld[i].first<<" "<<ld[i].second<<endl;
    }
    if(A==1){
        cout<<-1;
        return 0;
    }
    sort(ld,ld+n,cmp);
    
    double maxx=0;
    maxx=ld[0].second;
    int ans=1;
    for(int i=0;i<n;i++){
        if(ld[i].first>maxx){
            ans++;
            maxx=ld[i].second;
        }
        
    }
    cout<<ans;
    return 0;
}

Liver again!

King game

Original title link:

https://www.acwing.com/problem/content/116/

Title Description
Coincided with the national day of state H, the king invited n ministers to play a prize game.

First, he asked each minister to write an integer on his left and right hands, and the king himself wrote an integer on his left and right hands.

Then, let the n ministers line up and the king stand at the front of the line.

After lining up, all ministers will receive some gold coins rewarded by the king. The number of gold coins received by each minister is:

The product of the number on the left hand of everyone in front of the minister divided by the number on his own right hand and rounded down.

The king doesn't want a minister to get a lot of rewards, so he wants you to help him rearrange the order of the team, so that the minister who gets the most rewards will get as few rewards as possible.

Note that the king is always at the front of the team.

Input format
The first line contains an integer n representing the number of ministers.

The second line contains two integers a and b, separated by a space, representing the integers on the king's left hand and right hand, respectively.

The next n lines contain two integers a and b, separated by a space, representing the integers on each minister's left and right hand, respectively.

Output format
The output has only one line, including an integer, indicating the number of gold coins won by the minister who won the most reward in the rearranged team.

Data range
1≤n≤1000
0<a,b<10000

Input example:
3
1 1
2 3
7 4
4 6
Output example:
2

General idea of the topic

Each person has two points. The number of gold coins obtained by the current person is the product of the number on the left hand of all the previous people divided by the number on his own right hand, and then rounded down. Ask how the ranking can minimize the number of people who obtain the most gold coins. In addition, the first person does not participate in the ranking

Problem solving ideas

Directly sort all ministers according to the product of the numbers on the left and right hands from small to large, and the resulting sequence is the optimal queuing scheme, and then traverse once to get the largest number

AC code

#include<iostream>
#include<queue>
#include<algorithm>
#include<vector>
using namespace std;

const int N = 1100;
typedef pair<int,int> PII;
PII dc[N];

vector<int> max_vc(vector<int> a,vector<int> b){
    if(a.size()>b.size()) return a;
    else if(a.size()<b.size()) return b;
    if(vector<int>(a.rbegin(),a.rend())>vector<int>(b.rbegin(),b.rend())) return a;
    else return b;
}

vector<int> mul(vector<int> a,int b){
    vector<int> c;
    int k=0;
    for(int i=0;i<a.size();i++){
        k+=a[i]*b;
        c.push_back(k%10);
        k/=10;
    }
    while(k) c.push_back(k%10),k/=10;
    return c;
}

vector<int> dvl(vector<int> a,int b){
    vector<int> c;
    bool is_first = 0;
    for(int i=a.size()-1,t=0;i>=0;i--){
        t=t*10+a[i];
        int x=t/b;
        if(x||is_first){
            is_first = 1;
            c.push_back(x);
        }
        t%=b;
    }
    return vector<int>(c.rbegin(),c.rend());
}

void output(vector<int> a){
    for(int i=a.size()-1;i>=0;i--) cout<<a[i];
    return ;
}

int main(){
    int n;
    cin>>n;
    for(int i=0;i<=n;i++){
        int a,b;
        cin>>a>>b;
        dc[i]={a*b,a};
    }
    sort(dc+1,dc+1+n);
    
    vector<int> res(1,1);
    vector<int> ans(1,1);
    
    for(int i=0;i<=n;i++){
        if(i) res=max_vc(res,dvl(ans,dc[i].first/dc[i].second));
        ans=mul(ans,dc[i].second);
    }
    
    output(res);
    return 0;
}

Thinking and summarizing

In fact, the problem of greed is inseparable from a ranking problem.
The first thing we have to do is guess what it does,
Then prove your guess
If it is wrong, how to correct it
How to sort is the key
It is often used to write priority queue and pair, which also needs to be familiar with