1, What is the of a tree array
We first need to understand what a tree array is. A tree array is a data structure. Its main function is to efficiently realize interval summation and single point modification.
We can know that the most efficient interval summation is computation Prefix and Array thus
O
(
1
)
O(1)
O(1), but the time complexity of single point modification after finding the prefix and array is
O
(
n
)
O(n)
O(n) (the whole prefix and array need to be modified for a single point modification), so the time complexity of m-time interval summation and single point modification is
O
(
m
n
)
O(mn)
O(mn).
If you use an array to store all numbers, the complexity of interval summation is
O
(
n
)
O(n)
O(n), and the complexity of single point modification is
O
(
1
)
O(1)
O(1). Similarly, the time complexity of performing m interval summation and single point modification is the same
O
(
m
n
)
O(mn)
O(mn).
Therefore, the significance of tree array is to balance these two operations, so that the time complexity of interval summation and single point modification is O ( l o g n ) O(logn) O(logn). In this way, the time complexity of performing m interval summation and single point modification is O ( m ⋅ l o g n ) O(m·logn) O(m ⋅ logn).
2, Principle of tree array
How does a tree array operate? It's not a real tree. It's just an array shaped like a tree. Suppose we get a sequence q, we usually use tr[i] to record the tree array of this sequence. We assume that the last bit 1 in the binary of I is the penultimate k bit, so the meaning of tr[i] is the sum of the number k from the ith number of sequence q.
We can take a look at this diagram to understand what is stored in the tr array.
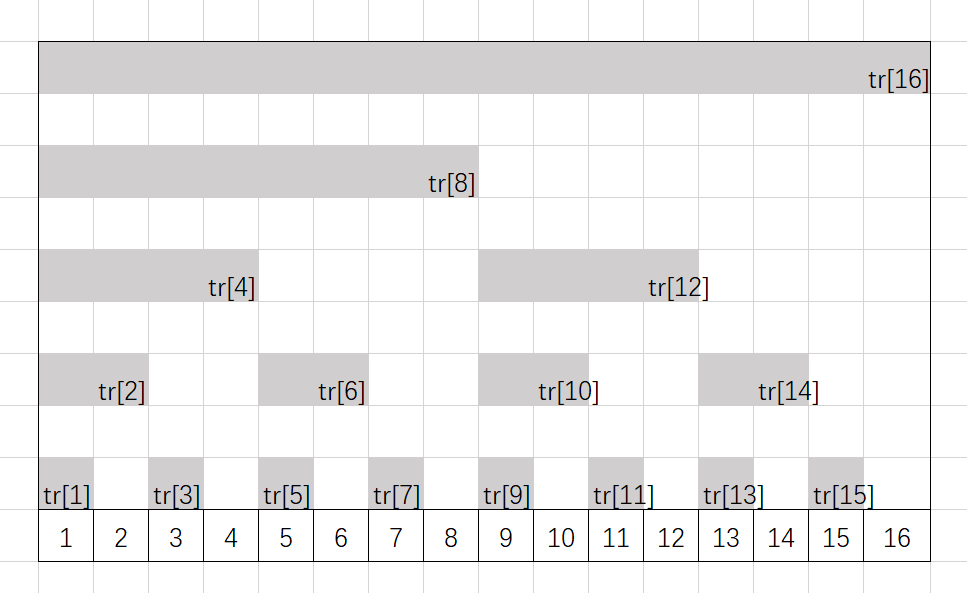
Each tr[i] here stores the sum of the gray parts. Because the last 1 of all odd numbers is in the last bit, tr[i] stores the ith number in the sequence q for the odd I.
Then we give each i of the tr array a dependency, as shown in the following figure:
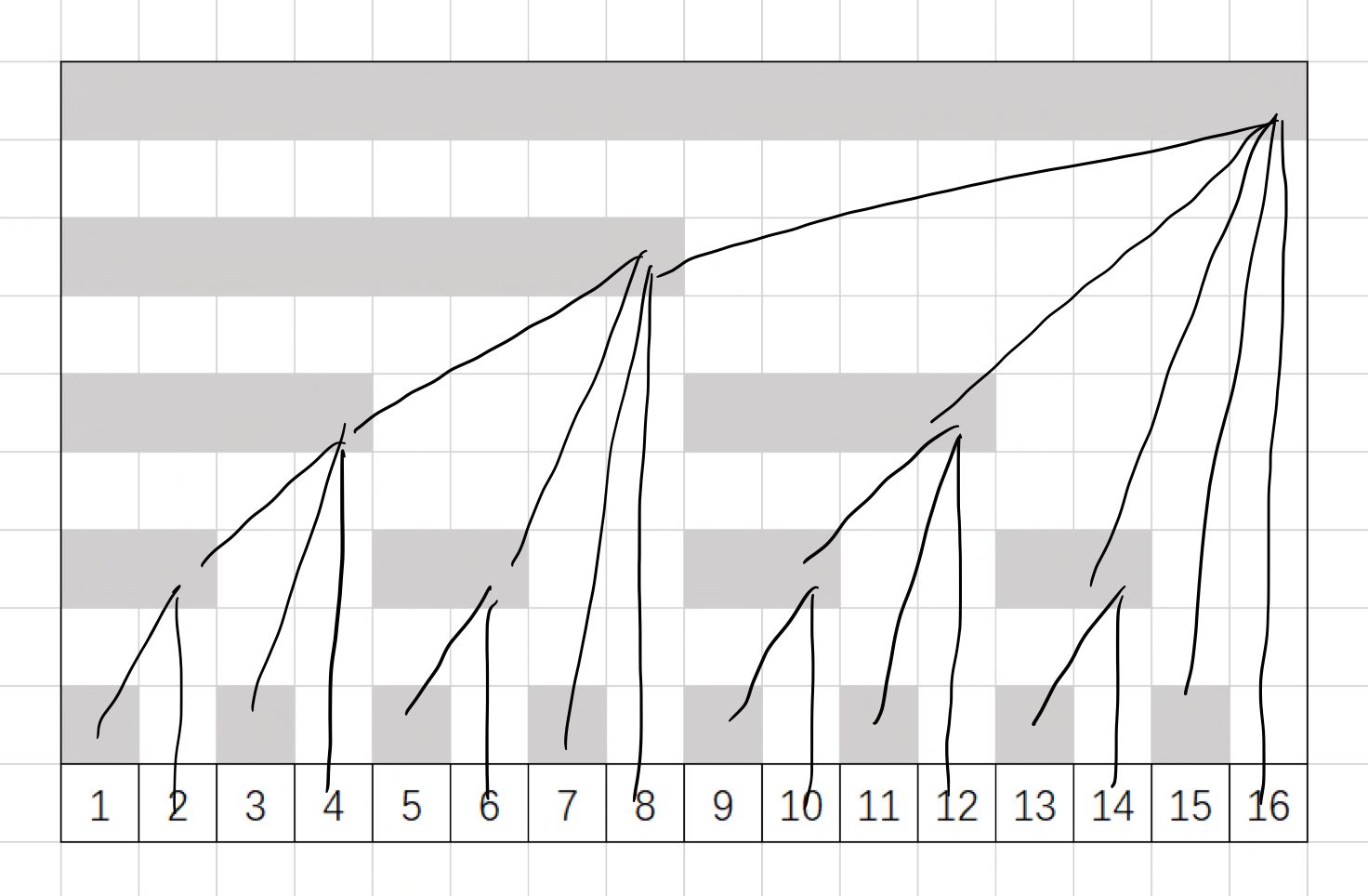
We record all the lines connected above as father and those connected below as son. In this way, the black lines between the top and bottom are very similar to a tree, so they are called tree array. So how to calculate each tr[i]? The value of tr[i] point is the sum of all the sons of point I. For example: tr[16]=tr[8]+tr[12]+tr[14]+tr[15]+q[16], tr[4]=tr[2]+tr[3]+q[4].
After understanding all the operations and principles, we still have a final problem, that is, how to find the last bit of a number, and what bit is 1. Here we need to use a very famous one lowbit operation , is the application of bit operation. Specifically, in the connection here, its role is to find out which bit is the last 1 in the binary form of a number. Therefore, we can use lowbit operation to find the father and son at a certain point. For a number x, its binary has m 1s, where each 1 corresponds to a son, so subtract its lowbit until 0, and all nodes within this are his sons; Similarly, a number x has been added to his lowbit until n, and all nodes within this are his father.
After understanding the principle, we will consider how to implement prefix and modification operations. For the modification operation, after modifying q[x], we use a whlie loop to let x += lowbit(x) until n. in this way, we find all the fathers of X and add k to all the accessed tr[x]. Because q[x] adds k, all his fathers have to add k (all fathers include q[x]).
For the query operation, we need to get the prefix sum of X, that is, all the summations of 1~x. therefore, we only need to access all the sons of point X and get the summation. Similarly, use a while loop, let x -= lowbit(x) until 0, and then let ans add tr[x] all the time to get the prefix and.
Because there are at most logn layers and one number x has at most logn 1, the time complexity of modification and query is
O
(
l
o
g
n
)
O(logn)
O(logn).
3, Basic code template
Template questions: P3374 tree array 1
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 500010;
int n,m,tr[N];
int lowbit(int x) //lowbit operation
{
return x & -x;
}
void add(int x,int k) //Modify the operation and add k to the x-th number
{
while(x <= n) //Modify all parent nodes
{
tr[x] += k; //All plus k
x += lowbit(x); //Find father
}
}
int sum(int x) //Query prefix sum and find the sum of 1~x
{
int res = 0;
while(x)
{
res += tr[x]; //res plus the sum of all sons
x -= lowbit(x); //Looking for a son
}
return res;
}
int main()
{
cin >> n >> m;
for(int i = 1;i <= n;i++)
{
int a;
cin >> a;
add(i,a);
}
while(m--)
{
int a,b,c;
cin >> a >> b >> c;
if(a == 1)
add(b,c);
else
cout << sum(c) - sum(b-1) << endl;
}
return 0;
}
4, Tree array advanced 1.0
The advanced use of tree array is to realize interval modification and single point query, which is what I need in O ( n l o g n ) O(nlogn) O(nlogn) is to add or subtract a number from an interval under time complexity, and can query the value of a point. If we use each number in the violent enumeration interval to perform the modification operation, the time complexity is O ( n 2 l o g n ) O(n^2logn) O(n2logn).
Realization thought
As soon as we see the interval modification here, we will think of a method to operate the interval—— Difference , we use a tree array to store this difference array. Every time we add k to interval [a,b], we just add k to tr[a] and subtract k from tr[b+1]. For a single point query, we only need to find the prefix sum of x, which is the number of position x.
Code template
Template questions: P3368 tree array 2
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 500010;
typedef long long LL;
int n,m,tr[N];
int lowbit(int x)
{
return x & -x;
}
void add(int x,int k)
{
for(int i = x;i <= n;i += lowbit(i))
tr[i] += k;
}
LL sum(int x)
{
LL res = 0;
for(int i = x;i;i -= lowbit(i))
res += (LL)tr[i];
return res;
}
int main()
{
cin >> n >> m;
int pre = 0;
for(int i = 1;i <= n;i++)
{
int a;
cin >> a;
add(i,a-pre); //Residual fraction group
pre = a;
}
while(m--)
{
int a;
cin >> a;
if(a == 1)
{
int x,y,k;
cin >> x >> y >> k;
add(x,k); //Position of x + k
add(y+1,-k); //The position of y+1 minus k, then the [x,y] interval increases k
}
else
{
int x;
cin >> x;
cout << sum(x) << endl;
}
}
return 0;
}
5, Tree array advanced 2.0
We know the single point modification and single point query, interval modification and single point query of tree array, so can we realize interval modification and interval query? This is the use of advanced 2.0.
Realization thought
We know that interval modification should be used Difference Therefore, we find his law on the basis of the difference group. Using the tree array to save the difference score group can quickly realize the interval modification, so how to calculate the interval sum? We know that the prefix and array are used to sum the interval, so we need to derive the prefix and array from his difference group. Because tr [] array is a stored differential array, let's write the calculation method of each number q[i] in his sequence q, as shown in the following figure.

Then the prefix sum of sequence x is equal to
q
1
+
q
2
+
q
3
+
.
.
.
+
q
x
q_1+q_2+q_3+...+q_x
q1 + q2 + q3 +... + qx, so we complete the matrix on the right of the above equation and add an additional row at the top, as shown in the figure below.

We can be surprised to find that,
q
1
q_1
q1~
q
x
q_x
The prefix sum of qx , is equal to our differential tree array tr[1] added to tr[x], multiplied by (x+1) and subtracted from the red part:
i
∗
t
r
[
i
]
i*tr[i]
I * tr[i], so we get the formula:
s
u
m
(
x
)
=
(
t
r
[
1
]
+
t
r
[
2
]
+
.
.
.
+
t
r
[
x
]
)
∗
(
x
+
1
)
−
∑
i
=
1
n
i
∗
t
r
[
i
]
sum(x) = (tr[1]+tr[2] + ...+tr[x])*(x+1)-\sum_{i=1}^ni*tr[i]
sum(x)=(tr[1]+tr[2]+...+tr[x])∗(x+1)−∑i=1ni∗tr[i].
∑
i
=
1
n
t
r
[
i
]
\sum_{i=1}^n tr[i]
∑ i=1n ∑ tr[i] we can find the sum of intervals through the difference fraction group, and for the latter, we need to build a new one
i
∗
t
r
[
i
]
i*tr[i]
I * tr[i].
Code template
Template questions: Acwing243. A simple integer problem 2
#include<iostream>
#include<cstring>
#include<queue>
#include<algorithm>
using namespace std;
const int N = 100010;
typedef long long LL;
int n,m,a[N];
LL tr1[N],tr2[N]; //tr1 is a differential tree array and tr2 is a tree array of i*tr[i]. Note that long long is on
int lowbit(int x)
{
return x & -x;
}
void add(LL tr[],int x,LL k)
{
for(int i = x;i <= n;i += lowbit(i))
tr[i] += k;
}
LL sum(LL tr[],int x)
{
LL res = 0;
for(int i = x;i;i -= lowbit(i))
res += tr[i];
return res;
}
LL ans(int x) //Find the prefix and function of x
{
return sum(tr1,x) * (x+1) - sum(tr2,x); //According to the formula, find the prefix and sum of x
}
int main()
{
cin >> n >> m;
for(int i = 1;i <= n;i++)
{
cin >> a[i];
int b = a[i] - a[i-1]; //b is the difference
add(tr1,i,b); //tr1 construct difference score group
add(tr2,i,(LL)i*b); //tr2 build i * differential array
}
while(m--)
{
char c;
cin >> c;
if(c == 'Q')
{
int l,r;
cin >> l >> r;
cout << ans(r) - ans(l-1) << endl; //Prefix and subtraction are interval sum
}
else
{
int l,r,d;
cin >> l >> r >> d;
add(tr1,l,d),add(tr2,l,(LL)l*d); //Modify the left side of tr1 and tr2 at the same time
add(tr1,r+1,-d),add(tr2,r+1,-(LL)(r+1)*d); //Modify the edges of tr1 and tr2 at the same time
}
}
return 0;
}
6, Comprehensive application of tree array (classic example)
1. What is the largest number of any number dynamically
Classic example: AcWing 241. Loulan Totem
thinking
This problem is to give the coordinates of a pile of points in the coordinate system, and then find the number of schemes that can form a V figure from three points. We can find the number of schemes of all V by enumerating the points in the middle of v. the number of schemes of V with point i as the middle point is equal to the number greater than i on the left of point i
c
l
c_l
cl * times the number of numbers larger than i on the right side of point i
c
r
c_r
cr. Then the solution of this problem is transformed into a dynamic solution. i point is the largest of all the numbers on the left.
Then we can use the idea of buckets to treat each number as a bucket, sweep from left to right, and set the bucket of the number as 1. At the same time, we use the tree array to store these buckets. In this way, it can be modified dynamically, which is equivalent to add(i,1); And we find the interval sum of i~n is equivalent to finding how many numbers are larger than i, (because each number is set to 1, so the interval sum is equivalent to how many numbers are larger than i).
Similarly, we can find how many numbers larger than i are on the right of i by scanning backwards. Multiplying the two is the scheme number.
AC code
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 200010;
typedef long long LL;
int n,a[N],tr[N];
int bigger[N],lower[N];
int lowbit(int x)
{
return x & -x;
}
void add(int x,int c)
{
for(int i = x;i <= n;i += lowbit(i))
tr[i] += c;
}
int sum(int x)
{
int res = 0;
for(int i = x;i;i -= lowbit(i))
res += tr[i];
return res;
}
int main()
{
cin >> n;
for(int i = 1;i <= n;i++)
cin >> a[i];
for(int i = 1;i <= n;i++)
{
int y = a[i];
bigger[i] = sum(n)-sum(y); //How many bigger numbers does bigger store than i
lower[i] = sum(y-1); //How many numbers are stored in lower that are smaller than i
add(y,1); //Give y disposal 1
}
memset(tr,0,sizeof tr); //Empty the tree array and scan it again from right to left
LL ansf = 0,ansb = 0;
for(int i = n;i;i--)
{
int y = a[i];
ansf += bigger[i] * (LL)(sum(n)-sum(y)); //After finding it, the left and right numbers are multiplied to be the number of schemes
ansb += lower[i] * (LL)sum(y-1);
add(y,1);
}
cout << ansf << " " << ansb << endl;
return 0;
}
2. What is the k-th largest number dynamically
Classic example: AcWing 244. Enigmatic cow
thinking
The question gives an n and how many cows are lower than him in front of each cow. Our usual practice is to start from the last cow and count forward. If there is a cow in front of the last cow
h
n
h_n
hn# a cow is lower than him, so he must be
h
n
+
1
h_n+1
The height of hn + 1, and then we will use it
h
n
+
1
h_n+1
The number hn + 1 is deleted from the sequence. Similarly, when we sweep to any i-th number, there is in front of him
h
i
h_i
If a cow is lower than him, then his height is the second in the current series
h
i
+
1
h_i+1
hi + the size of 1 number, and then delete the number after use. Therefore, we turn this problem into finding the number k in the sequence, and delete this number dynamically.
This is the basic operation of balanced tree, but we only know tree array, so we need to use tree array + bisection to solve this problem.
Similarly, using the idea of bucket, we set the tree array of all numbers from 1 to n to 1, indicating that these numbers have not been used. After using a number x, we give it the value of - 1, which is equivalent to add(x,-1); When finding the k-th largest number, we use dichotomy to find between 1 and N. when we find that the first sum(i) is equal to K, i is the k-th largest number (the sum of all numbers on the left of i is k-1, plus i is k, so i must be 1, he has not been used, and i is the k-th number). So the time complexity is
O
(
n
l
o
g
2
n
)
O(nlog^2n)
O(nlog2n).
AC code
#include<iostream>
#include<cstring>
#include<vector>
#include<algorithm>
using namespace std;
const int N = 100010;
typedef long long LL;
int n,a[N],tr[N];
vector<int> ans;
int lowbit(int x)
{
return x & -x;
}
void add(int x,int d)
{
for(int i = x;i <= n;i += lowbit(i))
tr[i] += d;
}
int sum(int x)
{
int res = 0;
for(int i = x;i;i -= lowbit(i))
res += tr[i] ;
return res;
}
int find(int x) //Binary search
{
int l = 1,r = n; //From 1 to n
while(l < r)
{
int mid = l+r>>1;
if(sum(mid) >= x) //If the midpoint is satisfied, move the right endpoint to the midpoint position
r = mid;
else //Otherwise, if the midpoint is not satisfied, move the left endpoint to the right of the midpoint
l = mid + 1;
}
return r;
}
int main()
{
cin >> n;
add(1,1); //Set 1 to 1
for(int i = 2;i <= n;i++) //Input from the second cow
{
cin >> a[i]; //Enter a[i]
add(i,1); //Initialization, set 1 to 1~n
}
for(int i = n;i;i--) //Cycle from back to front
{
int id = find(a[i]+1); //Bisection finds the number with the largest a[i]+1 and returns it to id
add(id,-1); //- 1 after use
ans.push_back(id); //Put in the answer array
}
for(int i = ans.size()-1;i >= 0;i--) //Output answer
cout << ans[i] << endl;
return 0;
}