🏳️‍🌈 Let's talk!!!! 🏳️‍🌈 Suzhou program Dabai 🏳️‍🌈

🍇 1. Time complexity of the algorithm

🍇 1.2. Methods for judging the advantages and disadvantages of procedures

• Consumption of computer resources and execution efficiency

• Computing algorithm execution time

• Time complexity (recommended)

🍇 1.3 time complexity

• Evaluation criteria: the number of operations / steps performed by the quantization algorithm

• The most important item: the most meaningful item of the time complexity expression

• The large o notation represents the time complexity: O (the most meaningful term in the quantitative expression)

def sumofN(n):
    theSum = 0
    for i in range(1, n+1):
        theSum = thSum + i
    return theSum

print(sumofN(10))
# 1 + n + 1  =====>   n + 2  =====>  O(n)
a = 5
b = 6
c = 10
for i in range(n):
    for j in range(n):
    	x = i * i
    	y = j * j
    	z = i * j
for k in range(n):
    w = a * k + 45
    v = b * b
d = 33

# 3 + 3n**2 + 2n + 1 ====> 3n**2 + 2n ====> 3n**2 ====> n**2 ====> O(n**2)

🍇 1.4 common time complexity

O(1) < O(logn) < O(n) < O(nlogn) < O(n^2) < O(n^3) < O(2^n) < O(n!) < O(n^n)

🍈 2. Stack

• Features: first in first out

• Application: each web browser has a back button. When you browse web pages, these pages are placed in a stack (actually the web address of the page). The page you are viewing now is at the top, and the first page you are viewing is at the bottom. If you press the 'back' button, you will browse the previous pages in the reverse order.

🍈 2.1. Implement a simple stack with python

Methods to be implemented

- Stack() //Create an empty new stack. It does not require parameters and returns an empty stack.
- push(item)    //Adds a new item to the top of the stack. It requires item as a parameter and does not return anything.
- pop()   //Removes the top item from the stack. It does not require parameters and returns item. The stack has been modified.
- peek()   //Returns the top item from the stack, but does not delete it. No parameters are required. Do not modify the stack.
- isEmpty()  //Test whether the stack is empty. No arguments are required and a Boolean value is returned.
- size()   //Returns the number of item s in the stack. No parameters are required and an integer is returned.
class Stark():
    def __init__(self):
        self.items = []
    def push(self, item):
        self.items.append(item)
    def pop(self):
        return self.items.pop()
	def peek(self):
        return len(self.items) - 1
    def isEmpty(self):
        return self,items == []
    def size(self):
        return len(self.items)

🍓 3. Queue

• Features: first in first out

• Application scenario:

Our computer laboratory has 30 computers connected to a printer. When students want to print, their print task is "consistent" with all other print tasks they are waiting for. The first entry task is to complete it first. If you are the last one, you must wait for all other tasks in front of you to print.

🍓 3.1. Implement a simple queue

- Queue() //Create an empty new queue. It does not require parameters and returns an empty queue.
- enqueue(item) //Add a new item to the end of the queue. It requires item as a parameter and does not return anything.
- dequeue() //Remove item from team leader. It does not require parameters and returns item. The queue was modified.
- isEmpty() //Check whether the queue is empty. It does not require parameters and returns a Boolean value.
- size() //Returns the number of items in the queue. It does not require parameters and returns an integer.
class Queue():
    def __init__(self):
        self.items = []
    def enqueue(self, item):
        self.items.insert(0, item)
    def dequeue(self):
        return self.items.pop()
    def isEmpty(self):
        return self.items == []
    def size(self):
        return len(self.items)

🍓 3.2 application (hot potato)

//Case: hot potato
// Introduction to the hot potato game: six children surround the city in a circle, and the order is specified by the children themselves. The first child has a hot potato in his hand. He needs to pass the potato to the next child after the timer counts for 1 second, and so on. The rule is that when the timer counts 7 seconds, the child with potato in his hand will quit the game. The game ends when one child is left, and the last child wins. Please use the queue to implement the game strategy. Which position will win in the end.
// Rule: team leader children should always have potato in their hands.
queue = Queue()
kids = ['A','B','C','D','E','F']
for kid in kids:
    queue.enqueue(kid)
while queue.size() > 1:
    for i in range(6):
        kid = queue.dequeue()
        queue.enqueue(kid)
    queue.dequeue()
    
print('The winners are:', queue.dequeue())

🍓 3.3 double ended queue

Compared with the queue, there are two heads and tails. It can insert and delete data at both ends, and provides the characteristics of stack and queue in single data structure

- Deque() //Create an empty new deque. It does not require parameters and returns an empty deque.
- addFront(item) //Add a new item to the header of deque. It requires the item parameter and does not return anything.
- addRear(item) //Add a new item to the tail of deque. It requires the item parameter and does not return anything.
- removeFront() //Delete the first item from deque. It does not require parameters and returns item. Deque was modified.
- removeRear() //Remove the tail from deque. It does not require parameters and returns item. Deque was modified.
- isEmpty() //Test whether deque is empty. It does not require parameters and returns a Boolean value.
- size() //Returns the number of items in deque. It does not require parameters and returns an integer.
class Dequeue():
    def __init__(self):
        self.items = []
    def isEmpty(self):
        return self.items == []
    def size(self):
        return len(self.items)
    def addFront(self, item):
        self.items.append(item)
    def addRear(self, item):
        self.items.insert(0, item)
    def removeFront(self):
        return self.items.pop()
    def removeRear(self):
        return self.items.pop(0)

Case: palindrome check

A palindrome is a string that reads the same characters at the beginning and end, for example, radar toot madam

def isHuiWen(s):
    ex = True
    
    q = Dequeue()
    
    for ch in s:
        q.addFront(ch)
        
    for i in range(len(s)//2):
        font = q.removeFront()
        rear = q.removeRear()
        if font != rear:
            ex = False
            break
    return ex
print(isHuiWen('addan'))

🍒 4. Linked list and sequential list

🍒 4.1 sequence table

• The elements stored in the collection are sequential. The structure of the sequential table can be divided into two forms: single data type and multi data type.

• Lists and tuples in python are sequential tables of multiple data types.

• Disadvantages of sequential table: the structure of sequential table needs to know the data size in advance to apply for continuous storage space, and the data needs to be relocated during expansion.

🍒 4.2 linked list

• Compared with sequential list, linked list structure can make full use of computer memory space, realize flexible memory dynamic management, and there is no need to move data when expanding.

• Linked list is a common basic data structure. It is a linear table, but it does not store data continuously like a sequential table. Instead, each node (data storage unit) stores the information (i.e. address) of the next node.

🍒 4.3. Construct linked list

is_empty(): //Is the linked list empty

length(): //Linked list length

travel(): //Traverse the entire linked list

add(item): //Add elements to the head of the linked list

append(item): //Add elements at the end of the linked list

insert(pos, item): //Add element at specified location

remove(item): //Delete node

search(item): //Find whether the node exists

node

class Node():
    def __init__(self,item):
        self.item = item
        self.next = None

Linked list

class Link():
    # Build an empty linked list
    def __init__(self):
        self._head = None // Always point to the head node in the linked list
    # Insert a node into the head of the linked list
    def add(self, item):
        node = Node(item)
        node.next = self._head
        self._head = node
    def travel(self):
        cur = self._head
        # If the linked list is empty, "empty linked list" is output
        if self._head = None:
            print("The linked list is empty")
        while cur:
            print(cur.item)
            cur = cur.next
    def isEmpty(self):
        return self._head == None
    def length(self):
        cur = self._head
        count = 0
        while cur:
            count += 1
            cur = cur.next
        return count
    def search(self, item):
        cur = self._head
        find = False
        while cur:
            if cur.item == item:
                find = True
                break
            cur = cur.next
        return find
    
    def append(self, item):
        node = Node(item)
        if self._head == None:
            self._head = node
            return
        
        cur = self._head
        pre = None
        while cur:
            pre = cur
            cur = cur.next
        pre.next = node
    def insert(self, pos, item):
        node = Node(item)
        
        if pos < 0 or pos > self.length():
            print("Give again pos assignment")
            
        cur = self._head
        pre = None
        
        for i in range(pos):
            pre = cur
            cur = cur.next
        pre.next = node
        node.next = cur
    def remove(self, item):
        cur = self._head
        pre = None
        
        if self._head == None:
            print("The linked list is empty and there are no nodes to delete")
            return
        
        # The first node is deleted
        if self._head.item == item:
            self._head = self._head.next
            return
        
        # The deleted node is not the first node
        while cur:
            pre = cur
            cur = cur.next
            if cur.item == item:
                pre.next = cur.next
                return

🍭 5. Sequential search

• When data is stored in a set such as a list, we say that the data has a linear or sequential relationship. Each data element is stored in a location relative to other data elements. Since these index values are ordered, we can access them in order. The search implemented in this process is sequential search.

Principle analysis of sequential search:

• Starting with the first element in the list, we sort in basic order, simply moving from one element to another until we find the element we are looking for or traverse the whole list. If we traverse the entire list, the element we are searching for does not exist.

• Code implementation: the function needs a list and the element we are looking for as parameters, and returns a Boolean value whether it exists or not. The found boolean variable is initialized to False. If we find an element in the list, it is assigned to True.

• Ordered list: previously, the elements in our list were placed randomly, so there was no relative order between the elements. What happens if the elements are sorted in some way? Can we achieve better efficiency in search technology?

Binary search: it must only be used in sequential tables

• The ordered list is very useful for our search implementation. In sequential search, when we compare with the first element, if the first element is not what we want to find, there are at most n-1 elements to compare. Binary search starts with the middle elements, not the list in order. If the element is the element we are looking for, we have completed the search. If it is not, we can use the ordered nature of the list to eliminate half of the remaining elements. If the element we are looking for is larger than the intermediate element, we can eliminate the intermediate element and half the elements smaller than the intermediate element. If the element is in the list, it must be in the large part. Then we can repeat the process with a large half, continuing to start with the intermediate element and compare it with what we are looking for.

🍭 5.1 implementation of binary search

def sort(alist, item):  // item is the element we are looking for
    low = 0  //The subscript of the first element in the list for the binary lookup operation
    high = len(alist)
    find = False
    
    while low <= high:
        mid = (low+high) // 2 # subscript of intermediate element
        if item > alist[mid]: // If the number we are looking for is larger than the middle number, it means that the number we are looking for is on the right side of the middle element
            low = mid + 1
        elif item < alist[mid]: // If the number we are looking for is smaller than the middle number, the number we are looking for is on the left of the middle number
            high = mid - 1
        else:
            find = True
            break
    return find

• test

alist = [1,2,3,4,5,6,7]
print(sort(alist, 51))

output:  False

🍊 6. Binary tree

• Root node

• Left leaf node

• Right leaf node

• subtree

• height

🍊 6.1 traversal of binary tree

• Breadth traversal: traversal layer by layer

• depth-first traversal

• Preamble: left and right root

• Middle order: left root right

• Post order: left and right root

🍊 6.2. Construct ordinary binary tree

class Node():
    def __init__(self, item):
        self.item = item
        self.left = None
        self.right = None
class Tree():
    # Construct an empty binary tree
    def __init__(self, item): // Root points to the address of the first node. If root points to None, it means that the binary tree is empty
        self.root = None
    # Inserts a node into a binary tree
    def addNode(self, item):
        node = Node(item)
        if self.root == None:
            # If addNode is called for the first time, it means that the first node is inserted into the empty tree, which must be the root node of the tree
            self.root = node
            return
        # If the above if is not executed, the tree is not empty. The following operation is to insert nodes into a non empty tree
        cur = self.root
        queue = [cur]
        while queue:
            n = queue.pop(0)
            if n.left != None:
                queue.append(n.left)
            else:
                n.left = node
                break
            if n.right != None:
                queue.append(n.right)
            else:
                n.right = node
                break
    def travel(self):
        # If empty
        if self.root == None:
            print("The tree is empty!")
            return
        
        cur = self.root
        queue = [cur]
        while queue:
            n = queue.pop(0)
            print(n.item)
            if n.left != None:
                queue.append(n.left)
            if n.right != None:
                queue.append(n.right)
    # Preorder traversal
    def forward(self, root):
        if root == None:
            return
        
        print(root.item)
        self.forward(root.left)
        self.forward(root.right)
        
    # Medium order traversal
    def middle(self, root):
        if root == None:
            return
        self.middle(root.left)
        print(root.item)
        self.middle(root.right)
        
    # Postorder traversal
    def back(self, root):
        if root == None:
            return
        self.back(root.left)
        self.back(root.right)
        print(root.item)

🍊 6.3. Construct sorted binary tree

class Node():
    def __init__(self, item):
        self.item = item
        self.left = None
        self.right = None
class SortTree():
    def __init__(self):
        self.root = None
    def insertNode(self, item):
        node = Node(item)
        # Insert the first node into the empty tree
        if self.root == None:
            self.root = node
            return
        # The tree is not empty
        cur = self.root
        
        while True:
            if node.item > cur.item: // Insert right
                if cur.right == None:
                    cur.right = node
                    break
                else:
                    cur = cur.right
            else: #Insert to the left
                if cur.left = None:
                    cur.left = node
                    break
                else:
                    cur = cur.left
    
    def forward(self, root):
        if root == None:
            return
        print(root.item)
        self.forward(root.left)
        self.forward(root.right)
        
    def middle(self, root):
        if root == None:
            return
        
        self.middle(root.left)
        print(root.item)
        self.middle(root.right)
    
    def back(self, root):
        if root == None:
            return
        
        self.back(root.left)
        self.back(root.right)
        print(root.item)

🍉 7. Implementation and explanation of eight sorting algorithms

🍉 7.1 bubble sorting

Main ideas:

1. Compare the adjacent elements and choose whether to exchange the two numbers according to the rules

2. From the first pair at the beginning to the last pair at the end

3. Repeat for multiple elements except the last one

• Time complexity: average O(n^2) best: O(n)

• Space complexity: O(1)

• Stability: stable
  
  C code implementation:

void bubble_sort(int *arr,int len)
{
    int i,j,tmp;
    int swap = 1;
    for(i = 0; i< len-1;i++)
    {
        for(j = 0; j< len -1 -i; j++)
            if(arr[j] > arr[j+1])
            {
                tmp = arr[j];
                arr[j] = arr[j+1];
                arr[j+1] = tmp;
                swap = 0;
            }
        if(swap)	//If there is no exchange, exit directly
            return;
    }
}

Python code implementation:

def bubble_sort(arr:[int])-> [int]:
    swap = True
    for i in range(0,len(arr)-1):
        for j in range(0,len(arr)-1-i):
            if arr[j] > arr[j+1]:
                arr[j],arr[j+1] = arr[j+1],arr[j]
                swap = False
        if swap:
            return arr
 
    return arr

🍉 7.2. Simple selection and sorting

Main idea: each time, select the record with the smallest keyword from the records to be sorted, and place it at the end of the sorted record sequence until the end of all sorting.

• Time complexity: O(n^2)

• Space complexity: O(1)

• Stability: unstable
  
  C code implementation:

void select_sort(int *arr,int len)
{
    int i,j,tmp;
    int min;
    for(i = 0;i<len;i++)
    {
        min = i;
        for(j=i + 1;j<len;j++)
            if(arr[j] < arr[min])
                min = j;
        tmp = arr[i];
        arr[i]=arr[min];
        arr[min] = tmp;
    }
}

Python code implementation:

def select_sort(arr:[int])-> [int]:
    for i in range(0,len(arr)):
        min_index = i
        for j in range(i+1,len(arr)):
            if arr[min_index] > arr[j]:
                min_index = j
        arr[min_index],arr[i] = arr[i],arr[min_index]
    return arr

🍉 7.3. Insert sort

Main idea: insert a record to be sorted into the appropriate position of the ordered queue according to the size of its keyword until all the records are inserted.

• Time complexity: average: O(n^2) best: O(n)

• Space complexity: O(1)

• Stability: stable

C code implementation:

void insert_sort(int *arr,int len)
{
    int i,j;
    int tmp = 0;
    for(i = 1;i< len;i++)
    {
        tmp  = arr[i];
        for(j = i-1;j>=0;j--)
            if(arr[j] > tmp)
                arr[j+1] = arr[j];
            else
                break;
        arr[j+1] = tmp;
 
    }
}

Python code implementation:

def insert_sort(arr:[int])-> [int]:
    for i in range(1,len(arr)):
        tmp = arr[i]
        j = i - 1
        while j>=0 and arr[j] > tmp:
            arr[j+1] = arr[j]
            j = j - 1
        arr[j+1] = tmp
    return arr

🍉 7.4 Hill sort (special insertion sort)

Shell sort, also known as reduced incremental sort, is an insert sort. It is an improved version of direct insertion sorting algorithm. The comparison times and movement times of Hill sort are less than those of direct insertion sort. When N is larger, the effect is more obvious.

Algorithm idea:

Let's take an example to describe the algorithm flow (excerpted from Wikipedia):

Suppose there is such a set of numbers {13, 14, 94, 33, 82, 25, 59, 94, 65, 23, 45, 27, 73, 25, 39, 10}, if we start sorting in steps of 5:

Before sorting	After sorting
13 14 94 33 82 25 59 94 65 23 45 27 73 25 39 10	10 14 73 25 23 13 27 94 33 39 25 59 94 65 82 45

When the above four lines of numbers are connected together in sequence, we get: {10, 14, 73, 25, 23, 13, 27, 94, 33, 39, 25, 59, 94, 65, 82, 45}, and then take 3 as the step:

Before sorting	After sorting
10 14 73 25 23 13 27 94 33 39 25 59 94 65 82 45	10 14 13 25 23 33 27 25 59 39 65 73 45 94 82 94

Finally, sort in steps of 1 (this is a simple insertion sort).

It is conceivable that the selection of step size is an important part of hill sorting. The algorithm starts with a certain step size, then continues to sort with a smaller step size, and finally the algorithm sorts with a step size of 1. When the step size is 1, the algorithm changes to direct insertion sorting, which ensures that all data will be sorted.

• Time complexity: average: O(nlogn) worst: O(n^2)

• Space complexity: O(1)

• Stability: unstable

C code implementation:

void shell_sort(int *arr,int len,int gap)
{
    int tmp;
    int i,j;
    for(i = gap; i<len; i = i+gap)
    {
        tmp = arr[i];
        for(j = i -gap;j>=0;j=j-gap)
            if(arr[j] > tmp)
                arr[j+gap] = arr[j];
            else
                break;
        arr[j+gap] = tmp;
    }
}
 
void Shell(int *arr,int len)
{
    int gap[] = {5,3,1};    //It can be divided into half of the step size, which is customized here
    int len_gap = sizeof(gap)/sizeof(gap[0]);
    for(int i=0;i<len_gap;++i)
        shell_sort(arr,len,gap[i]);
}

Python code implementation:

def shell_sort(arr:[int])->[int]:
    g = [5,3,1]
    for gap in g:
        for i in range(gap,len(arr)):
            tmp = arr[i]
            j = i-gap
            while j>=0 and arr[j] > tmp:
                arr[j+gap] = arr[j]
                j = j - gap
            arr[j+gap] = tmp
    return arr 

🍉 7.5 quick sort

The basic idea of quick sort is to divide the data to be sorted into two independent parts through one-time sorting: the number on the left of the split point is smaller than it, and the number on the right is larger than it.

• Time complexity: average: O(nlogn) worst: O(n^2)

• Space complexity: O(logn)

• Stability: unstable

Then quickly sort the two parts of data according to this method. The whole sorting process can be recursive, so as to turn the whole data into an ordered sequence.

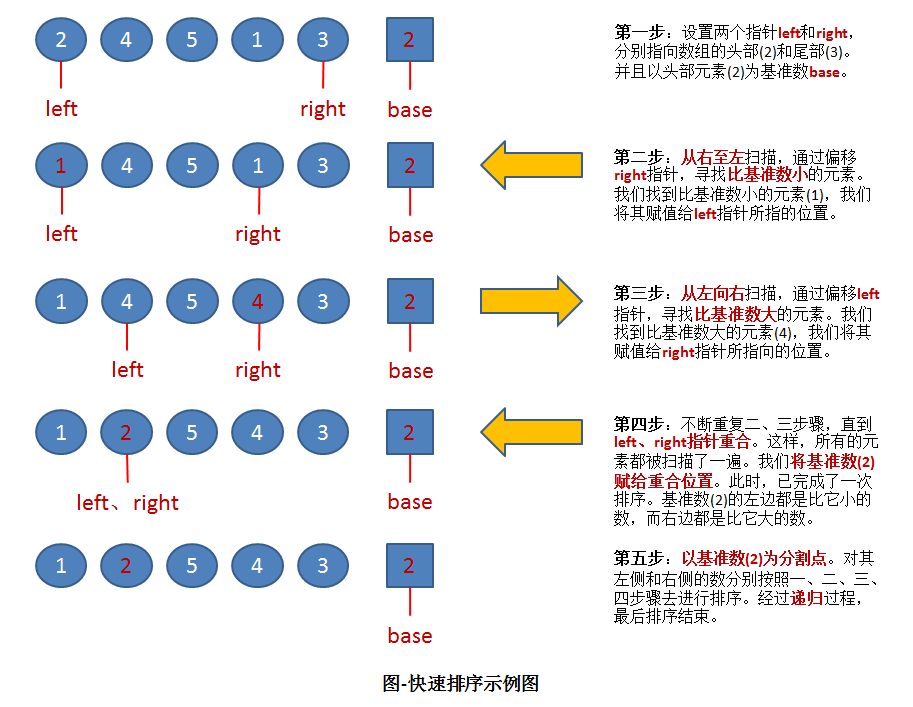
C code implementation:

int division(int *arr,int left,int right)
{
    //Take the benchmark number as the leftmost number each time
    int base = arr[left];
    while(left<right)
    {
        //Start at the right end and look to the left. When finding a value less than the reference number, put the element to the left
        while(left<right && arr[right] >= base)
            --right;
        arr[left] = arr[right];
        //Similarly, when found, turn to the left and start to find to the right, and put the value greater than the benchmark number to the right of the element
        while(left<right && arr[left] <= base)
            ++left;
        arr[right] = arr[left];
    }
    // Finally, put the base in the left position. At this time, the values on the left side of the left position should be smaller than left;
    // The values on the right side of the left position should be greater than that of left
    arr[left] = base;
    return left;
}
 
void quick_sort(int *arr,int left,int right)
{
    //The left subscript should be smaller than the right subscript, otherwise it will cross the boundary
    if( left < right)
    {
        //Divide the array according to the reference number
        int base = division(arr,left,right);
        //Recursion is performed on the left and right sides respectively
        quick_sort(arr,left,base-1);
        quick_sort(arr,base+1,right);
    }
}
 

Python code implementation:

def quick_sort(arr:[int],left:int,right:int)->[int]:
    def division(arr:[int],left:int,right:int):
        base = arr[left]
        while left < right:
            while left < right and arr[right] >= base:
                right -= 1
            arr[left] = arr[right]
            while left < right and arr[left] <= base:
                left += 1
            arr[right] = arr[left]
        arr[left] = base
        return left
 
    if(left<right):
        base = division(arr,left,right)
        quick_sort(arr,left,base-1)
        quick_sort(arr,base+1,right)
    return arr

🍉 7.6 heap sorting

Heap sorting is a sort of selection.

Heap is a complete binary tree stored sequentially.

• The keyword of each node is not greater than the keyword of its child node. Such a heap is called small root heap.

• The keyword of each node is not less than the keyword of its child node. Such a heap is called large root heap.

For example, a sequence {R0, R1,..., Rn} of n elements is called a heap if and only if one of the following relationships is satisfied:

• RI < = r2i + 1 and RI < = r2i + 2 (small root pile)

• RI > = r2i + 1 and RI > = r2i + 2 (large root heap)

Where i=1,2,..., n/2 rounded down;

• Time complexity: O(nlogn)

• Space complexity: O(1)

• Stability: unstable

🍉 7.7 merging and sorting

The algorithm adopts the classical divide and conquer strategy (the divide and conquer method divides the problem into some small problems and then solves them recursively, while the conquer stage "fixes" the answers obtained in different stages, that is, divide and conquer).

• Time complexity: O(nlog2n)

• Space complexity: O(n)

• Stability: stable

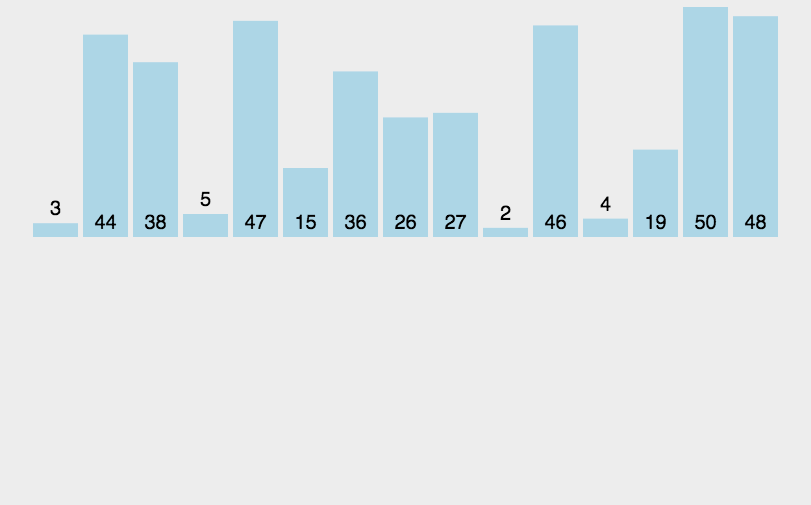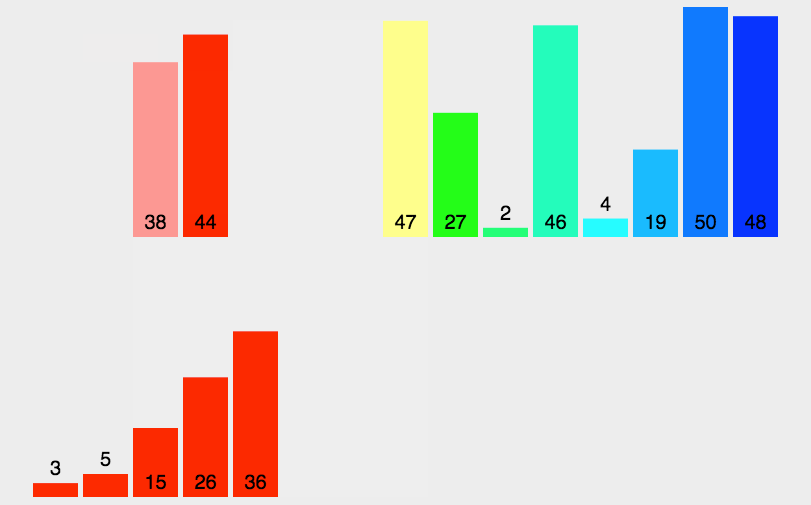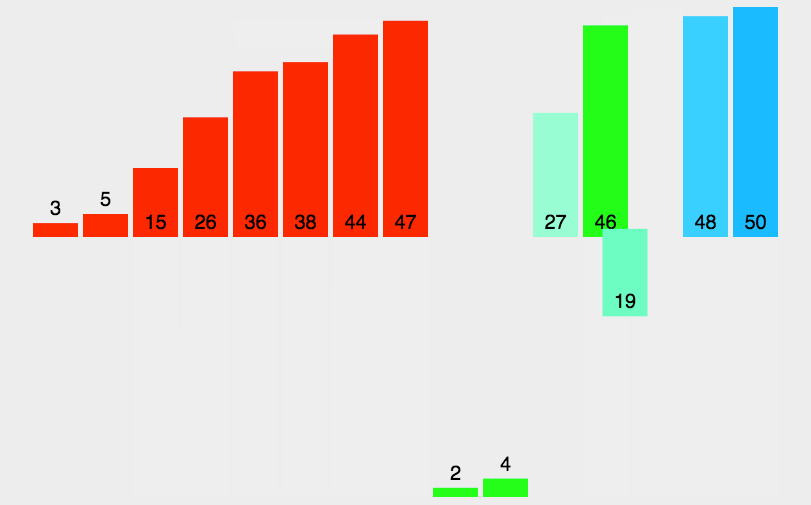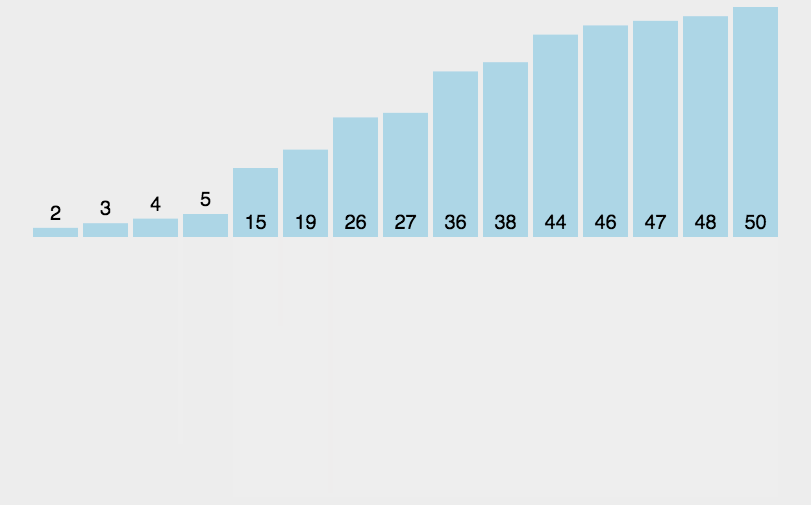
🍉 7.8. Cardinality sorting

Basic idea: unify all the values to be compared (positive integers) into the same digit length, and fill zero in front of the number with shorter digits. Then, start from the lowest bit and sort in turn. In this way, after sorting from the lowest bit to the highest bit, the sequence will become an ordered sequence.

Algorithm steps:

• All values to be compared (positive integers) are unified into the same digit length, and the number with shorter digits is preceded by zero.

• Start from the lowest order and sort once.

• In this way, the sequence becomes an ordered sequence from the lowest order to the highest order.

The radix sorting method can be LSD (Least significant digital) or MSD (Most significant digital). The sorting method of LSD starts from the far right of the key value, while MSD starts from the far left of the key value.

Let's show how cardinality sorting is carried out through a specific example. There is an initial sequence: R {50, 123, 543, 187, 49, 30, 0, 2, 11, 100}.

We know that the cardinality of each digit of any Arabic number is expressed by 0 ~ 9, so we might as well regard 0 ~ 9 as 10 barrels.

We first classify the sequence according to the number of single digits and divide it into the specified bucket. For example, R[0] = 50, the number of single digits is 0, and store this number into the bucket numbered 0.

After classification, we take all the numbers from each bucket in the order from No. 0 to No. 9. At this time, the obtained sequence is the sequence with an increasing trend in single digits.

Sort by single digit: {50, 30, 0, 100, 11, 2, 123, 543, 187, 49}.

Next, you can sort the tens and hundreds of digits in this way, and finally you can get the sorted sequence.

• Time complexity: O(dn)

• Space complexity: O(n)

• Stability: stable
  

🌟 8. Author related articles and resource sharing 🌟

🌟 Let the world have no technology that can't be learned 🌟
Learning C# is no longer a difficult problem
🌳 C# getting started to advanced tutorial 🌳
Relevant C# practical projects
👉 C#RS232C communication source code 👈
👉 C # entrusted data transmission 👈
👉 C# Modbus TCP source code 👈
👉 C# warehouse management system source code 👈
👉 C# Omron communication Demo 👈
👉 C# Omron communication Demo 👈
👉 2021C# and Halcon vision common framework 👈
✨ For C# project, please check your home page ✨
🌟 Machine vision, deep learning 🌟
🌌 Halcon introduction to mastery 🌌
🌌 In depth learning materials and tutorials 🌌
Machine vision, deep learning and actual combat
👉 2021 C#+HALCON vision software 👈
👉 In 2021, C#+HALCON will realize template matching 👈
👉 C# integrates Halcon's deep learning software 👈
👉 C# integrated Halcon's deep learning software with [MNIST example] data set 👈
👉 C # halcon WPF open source form control that supports equal scaling and dragging 👈
👉 Labview and HALCON in 2021 👈
👉 Labview and Visionpro in 2021 👈
👉 Automatic identification module of brake pad thickness of EMU based on Halcon and VS 👈
✨ For machine vision and in-depth learning, welcome to your personal home page ✨
🌟 Java, database tutorials and projects 🌟
🍏 Introduction to JAVA advanced tutorial 🍏
🍏 Getting started with database to advanced tutorial 🍏
Actual combat of Java and database projects
👉 Java classic nostalgic bully web game console source code enhanced version 👈
👉 Java property management system + applet source code 👈
👉 Design and implementation of JAVA hotel room reservation management system SQLserver 👈
👉 Research and development of JAVA library management system MYSQL 👈
✨ For Java, database tutorials and project practice, welcome to your personal home page ✨
🌟 Share Python knowledge, explain and share 🌟
🥝 Python knowledge and project column 🥝
🥝 "Python detects the tremble, concerns the account number tiktok". 🥝
🥝 Teach you how to install and use Python+Qt5 🥝
🥝 Q & A on the fundamentals of python Programming in 10000 words to Xiaobai 🥝
🥝 Python drawing Android CPU and memory growth curve 🥝
About Python project practice
👉 Python library management system based on Django 👈
👉 Python management system 👈
👉 Nine commonly used python crawler source codes in 2021 👈
👉 python QR code generator 👈
✨ For Python tutorial and project practice, welcome to your personal home page ✨
🌟 Share the interview questions and interview process of major companies 🌟
🍏 The latest VUE interview questions of gold, nine and silver in 2021 ☀️ < ❤️ Remember to collect ❤️>>🍏
🍏 As long as you read 10000 words carefully ☀️ Linux Operating System Basics ☀️ Hang the interviewer every minute< ❤️ Remember to collect ❤️>>🍏
🍏 < ❤️ Give Xiaobai a comprehensive explanation of the basics of python Programming in 10000 words ❤️ < 😀 Remember to collect, or it will disappear 😀>>🍏
✨ About the interview questions and interview process of major companies, you are welcome to view your personal home page ✨

🏳️‍🌈 Pay attention to Suzhou program disclosure and continuously update technology sharing. Thank you for your support 🏳️‍🌈

❤️ Pay attention to the official account of Suzhou procedures ❤️

👇 👇👇