catalogue
2, Downward adjustment algorithm of heap
4, Heap up adjustment algorithm
5. Get data from the top of the heap
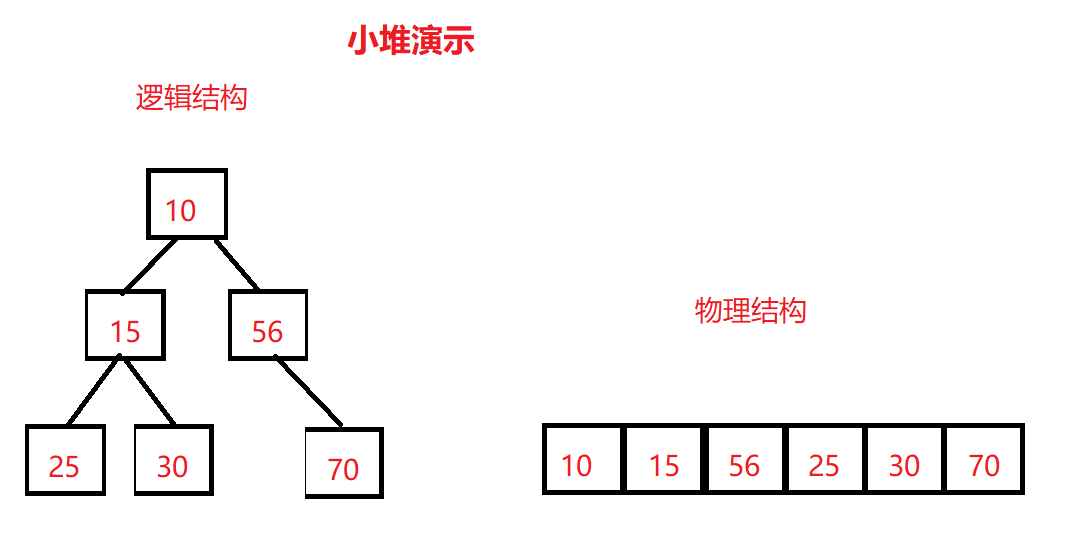
1, Pile
1. Concept of heap
Heap: if there is a key set K={k0,k1,k2,..., kn-1}, all its elements are stored in a one-dimensional array in the order of a complete binary tree, and meet ki < = k2i + 1 and Ki < = k2i + 2 (or ki > = k2i + 1 and Ki > = k2i + 2), where i=0,1,2,..., the set is called heap.
2. Nature of heap
① The value of a node in the heap is always not greater than or less than the value of its parent node;
② Heap is always a complete binary tree.
3. Heap classification
Heap: the heap with the largest root node is called the maximum heap or large root heap. The value of the parent node is always greater than that of the child.
Small heap: the heap with the smallest root node is called the minimum heap or small root heap. The value of the parent node is always less than that of the child.
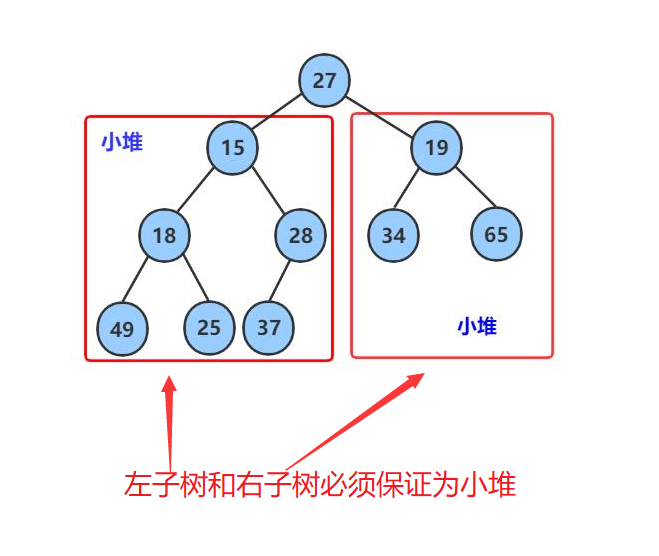
2, Downward adjustment algorithm of heap
Now we give an array, which is logically regarded as a complete binary tree. We can adjust it into a small heap through the downward adjustment algorithm starting from the root node. The downward adjustment algorithm has a premise: the left and right subtrees must be a heap before adjustment.
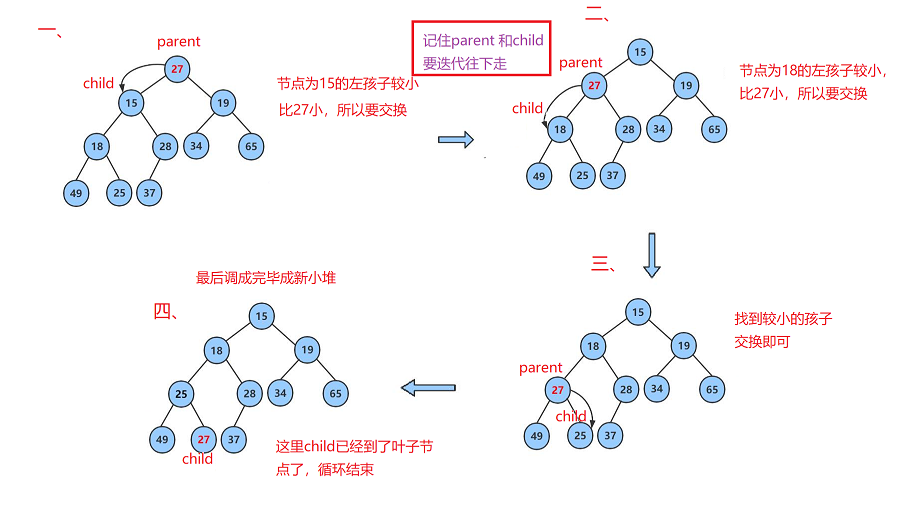
Basic idea of downward adjustment algorithm: (take the construction of small piles as an example)
① Starting from the root node, select the smaller value of the left and right child nodes
② Compare fathers with younger children
If the father is larger than the child, then exchange
If the father is smaller than this child, no exchange will be made
③ End condition
1. Father < = small children stop
2. Adjust to the leaf node (the leaf node is characterized by no left child, that is, if the array subscript exceeds the range, it does not exist)
The code is as follows:
void Swap(int* x,int* y)
{
int*tmp=*x;
*x=*y;
*y=tmp;
}
void AdjustDown(int* a, int n, int parent) //Note that the right child may not exist
{
//Child records the subscript of the smaller child in the left and right children
int child = 2 * parent + 1; //First, the value of the left child is smaller by default
while(child<n)
{
if (child + 1 < n && a[child + 1] < a[child])//The right child exists and the right child is smaller than the left child
{
child++;//The younger child is changed to the right child
}
if (a[child < a[parent]])
{
Swap(&a[child], & a[parent]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}Detailed downward adjustment algorithm process:
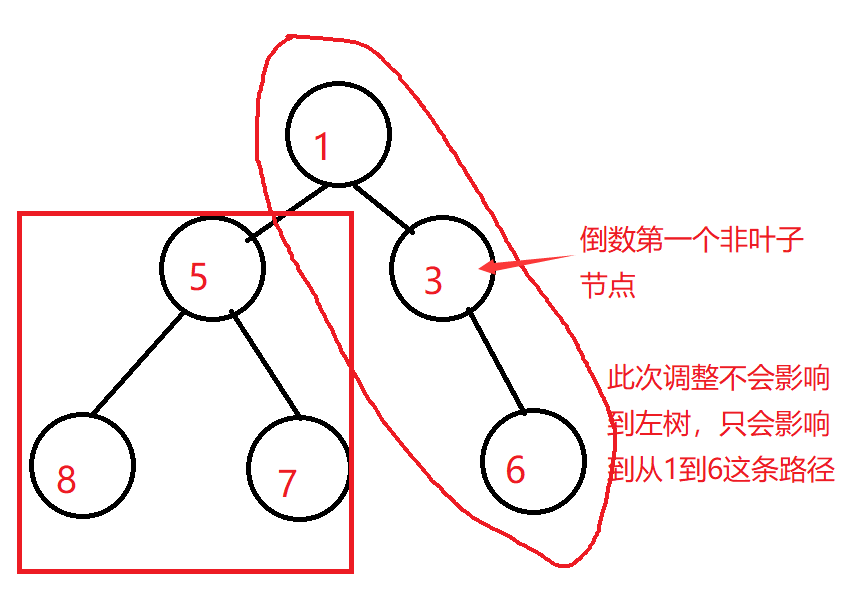
3, Heap creation
How to adjust an arbitrary tree to heap?
Here, we can use the heap downward adjustment algorithm just written. We know that to meet the heap, the left and right subtrees must be large or small piles. We can use this idea to walk backwards from bottom to top, starting from the first non leaf node, and adjust it downward as a root through the control of array subscript, Until the current path is adjusted to a large or small pile that meets the conditions
The code is as follows:
//Build heap n is the number of arrays, n-1 is the subscript (n-1-1) / 2 of the last element, and find the father of the first non leaf node
for (int i = (n - 1 - 1) / 2; i >= 0; i--)
{
AdjustDown(hp->a, hp->size, i);
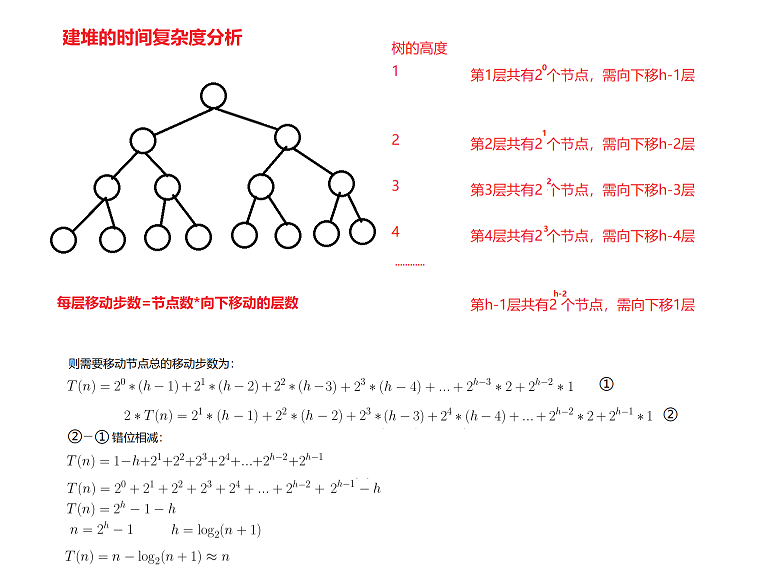
}The time complexity of heap building is O(N)
Because the heap is a complete binary tree, and the full binary tree is also a complete binary tree, the full binary tree is used here for simplification (the time complexity is an approximate value, and more nodes do not affect the final result):
4, Heap up adjustment algorithm
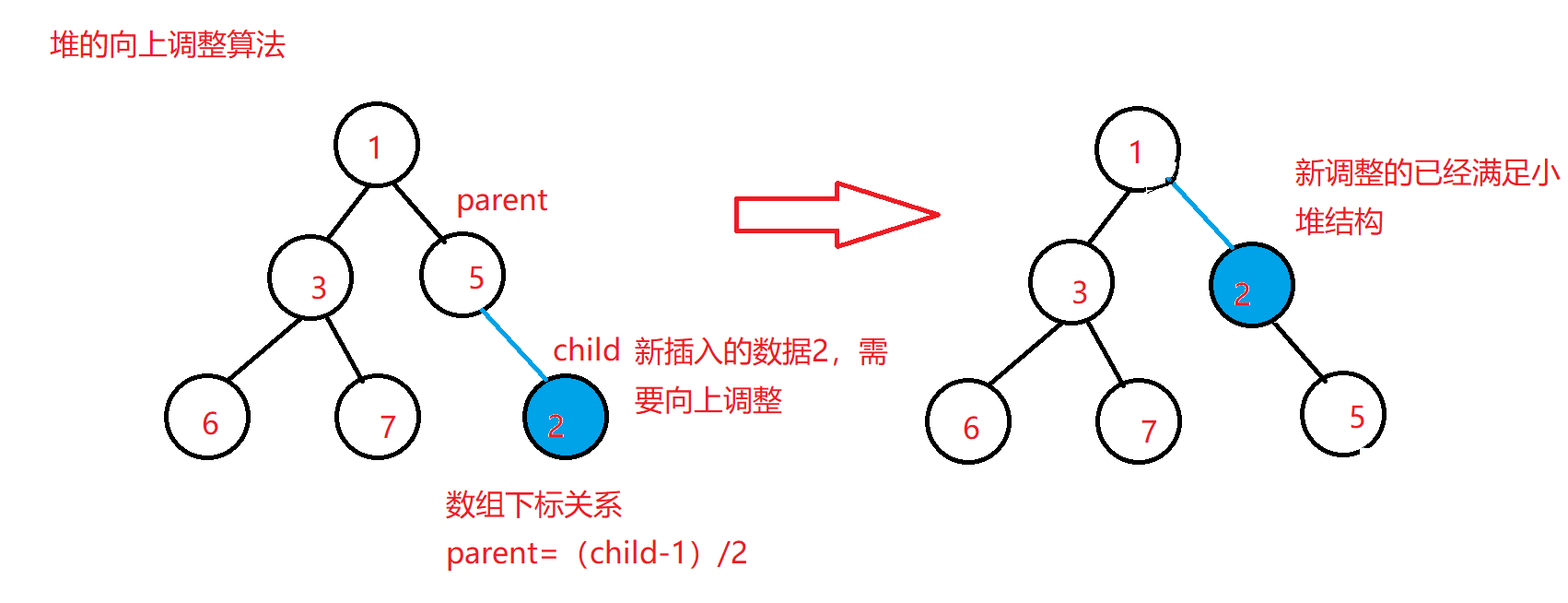
When we already have a heap, we need to insert data at the end of the heap and adjust it to keep the heap structure. Here we need to use the heap up adjustment algorithm
Basic idea of heap up adjustment algorithm: (taking building a small heap as an example)
① Compare the data to be inserted with its parent node data
② If the data of the child node is less than the data of the parent node, it is exchanged
If the data of the child node is larger than the data of the parent node, no exchange and adjustment are required, and the heap structure has been met
The code is as follows:
void Swap(int* x, int* y)
{
int* tmp = *x;
*x = *y;
*y = tmp;
}
void AdjustUp(int * a, int child)
{
int parent = (child - 1) / 2;
while (child>0)
{
if (a[parent] > a[child])
{
Swap(&a[child],&a[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}
Detailed upward adjustment algorithm:
Now that we know the heap up and down adjustment algorithms, we can start to implement the heap structure
5, Implementation of heap
We need a structure to represent the heap
typedef int HPDataType;//Facilitate subsequent modification of data types
typedef struct Heap
{
HPDataType* a;//Pointer for dynamic development
int size;
int capacity;
}Heap;1. Heap initialization
We still set size and capacity to 0 and array a to NULL.
void HeapInit(Heap* hp)
{
assert(hp);
hp->capacity = hp->size = 0;
hp->a = NULL;
}2. Heap destruction
The array used for dynamic development should be released and returned to the operating system in order to avoid memory leakage
void HeapDestroy(Heap* hp)
{
assert(hp);
free(hp->a);//Release dynamic array
hp->a = NULL;//Empty in time
hp->capacity =hp->size = 0;//Set the number of elements to 0
}3. Heap insertion
After inserting data into the heap, its structure will still be the heap, so we need to adjust it upward. At the beginning, both size and capacity are 0, so we need to expand the capacity first and then put the data in
void HeapPush(Heap* hp,HPDataType x)
{
assert(hp);
if (hp->capacity == hp->size)
{
size_t newcapacity = hp->capacity == 0 ? 4 : hp->capacity * 2;
HPDataType* tmp = (HPDataType*)realloc(hp->a, sizeof(HPDataType) * newcapacity);
if (tmp == NULL)
{
printf("realloc fail\n");
exit(-1);
}
hp->a = tmp;
hp->capacity = newcapacity;
}
hp->a[hp->size] = x;
hp->size++;
AdjustUp(hp->a, hp->size - 1);
}4. Deletion of heap
Deleting the heap is to delete the data at the top of the heap, exchange the data at the top of the heap with the last data, and then delete the last data. The remaining data can be adjusted downward. Due to the array structure, we only need size -- which is equivalent to deleting that data
void HeapPop(Heap* hp)
{
assert(hp);
assert(!HeapEmpty(hp));
Swap(&hp->a[0],&hp->a[hp->size-1]);
hp->size--;
AdjustDown(hp->a,hp->size,0);
}5. Get data from the top of the heap
We can directly use the array subscript to return data
//Take the data from the top of the heap
HPDataType HeapTop(Heap* hp)
{
assert(hp);
assert(!HeapEmpty(hp));
return hp->a[0];
}6. Number of data in the heap
Just return size directly
//Total number of data in the heap
int HeapSize(Heap* hp)
{
assert(hp);
return hp->size;
}7. Empty judgment of heap
Judge whether the number of data in the heap is 0
//Empty judgment of heap
bool HeapEmpty(Heap* hp)
{
assert(hp);
return hp->size == 0;//0 is false, not 0 is true
}8. Heap printing
void HeapPrint(Heap* hp)
{
assert(hp);
for(int i = 0; i < hp->size; i++)
{
printf("%d ",hp->a[i]);
}
printf("\n");
}9. Test small example
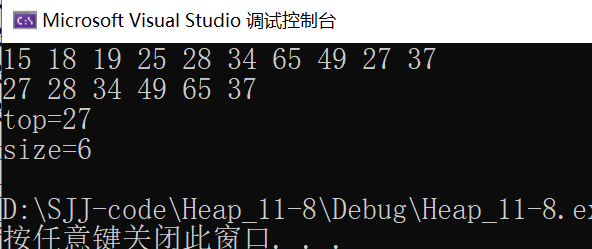
#include"Heap.h"
int main()
{
int arr[] = { 27,15,19,18,28,34,65,49,25,37 };
Heap hp;
HeapInit(&hp);
int i = 0;
for (i = 0; i < sizeof(arr) / sizeof(arr[0]); i++)
{
HeapPush(&hp, arr[i]);
}
HeapPrint1(&hp);
HeapPop(&hp);
HeapPop(&hp);
HeapPop(&hp);
HeapPop(&hp);
HeapPrint1(&hp);
printf("top=%d\n", HeapTop(&hp));
printf("size=%d\n",HeapSize(&hp));
HeapDestroy(&hp);
return 0;
}test result
6, Topk problem
That is, find the first K largest or smallest elements in the data combination. Generally, the amount of data is relatively large.
For example, the top 10 professional players, the world's top 500, the rich list, the top 100 active players in the game, etc.
For the Top-K problem, the simplest and direct way you can think of is sorting. However, if the amount of data is very large, sorting is not desirable (maybe all the data can not be loaded into memory at once). The best way is to use heap. The basic idea is as follows:
1. Use the first K elements in the data set to build the heap
For the first k largest elements, build a small heap
For the first k smallest elements, build a lot
2. Compare the remaining N-K elements with the top elements in turn. If not, replace the top elements
After comparing the remaining N-K elements with the top elements in turn
3. The remaining K elements in the heap are the first K minimum or maximum elements
The code is as follows:
//topk problem
void PrintTopK(int* a, int n, int k)
{
// 1. Build a heap -- build a heap with the first k elements in a (insert one by one)
Heap hp;
HeapInit(&hp);
for(int i=0;i<k;i++)
{
HeapPush(&hp,a[i]);
}
// 2. Exchange the remaining n-k elements with the top elements in turn, and replace them if they are not satisfied
for (int i = k; i < n; i++)
{
if (a[i] > HeapTop(&hp))
{
HeapPop(&hp);
HeapPush(&hp,a[i]);
}
}
HeapPrint(&hp);
HeapDestroy(&hp);
}Test topk
void TestTopk()
{
int n = 10000;
int* a = (int*)malloc(sizeof(int) * n);
srand((unsigned int)time(0));
for (size_t i = 0; i < n; ++i)
{
a[i] = rand() % 1000000;
}
a[5] = 1000000 + 1;
a[1231] = 1000000 + 2;
a[531] = 1000000 + 3;
a[5121] = 1000000 + 4;
a[115] = 1000000 + 5;
a[2335] = 1000000 + 6;
a[9999] = 1000000 + 7;
a[76] = 1000000 + 8;
a[423] = 1000000 + 9;
a[3144] = 1000000 + 10;
PrintTopK(a, n, 10);
}
int main()
{
TestTopk();
return 0;
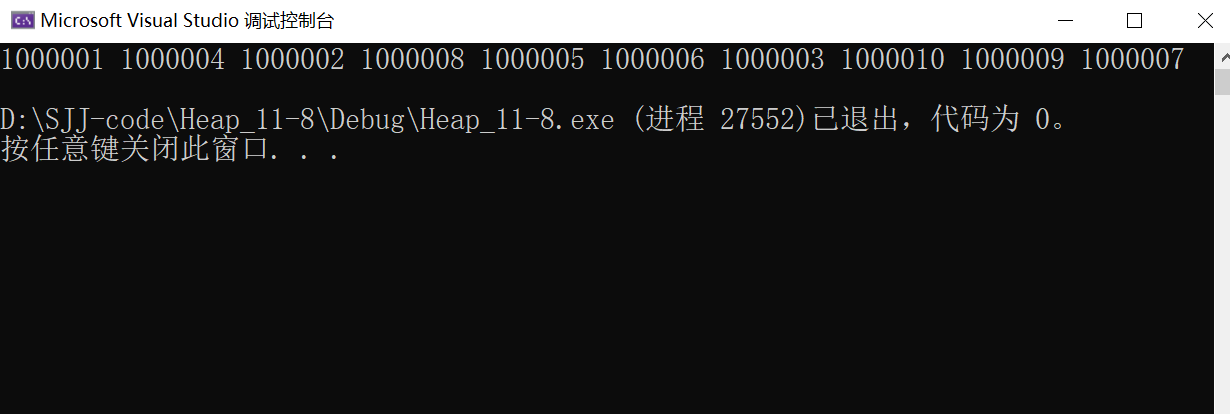
}Here, we use the random number generation method to randomly generate 10000 numbers less than 100000, and then randomly construct 10 numbers greater than 100000. We can find these 10 numbers greater than 100000 by using Topk function!
Test results:
Thank you for watching!