1, Tree

A tree t is a set of non empty finite elements, one of which is the root, and the other elements form the subtree of t. As shown in the figure:

Each element represents a node. The tree root is painted on the top and its subtree is painted on the bottom. There is an edge between the root and the root of the subtree. Similarly, each subtree is also rooted on it and its subtree is under it. In a tree, an element node and its child nodes are connected by edges. For example, in the above figure, ANN, Mary and John are Joe's children and Joe is their parents. Children of the same parents are brothers. In the picture, ANN, Mary and John are brothers, while Mark and Chris are not brothers. There are other terms: grandson, grandfather, ancestor, offspring, etc. An element without children in a tree is called a leaf.
Another common term for trees is level. The root is level 1, the child is level 2, the child is level 3, etc. The height or depth of a tree is the number of intermediate trees. In the above figure, the height of the tree is 3. The degree of an element refers to the number of children. The degree of leaf node is 0. The degree of a tree is the maximum of the degree of its elements.

2, Binary tree

1. Definition of binary tree

A binary tree t is a set of finite elements. When the binary tree is not empty, one element is called the root, and the remaining elements are divided into two binary trees, which are called the left subtree and the right subtree of t.

The fundamental difference between binary tree and tree lies in:
Each element of a binary tree has exactly two subtrees (one or two of which may be empty). Each element of the tree can have any number of subtrees.
In a binary tree, the subtrees of each element are ordered, that is, there are left subtrees and right subtrees. The subtree of the tree can be disordered.

2. Characteristics of binary tree

Feature 1 a binary tree has n elements, n > 0 n \gt 0 n> 0, which has n - 1 edges.
Feature 2 the height of a binary tree is h, h ≥ 0 h \ge 0 H ≥ 0, it has at least h elements and at most 2 h − 1 2^h - 1 2h − 1 element.
Feature 3 a binary tree has n elements, n > 0 n \gt 0 n> 0, its maximum height is n and its minimum height is ⌈ l o g 2 ( n + 1 ) ⌉ \lceil log_2(n+1) \rceil ⌈log2​(n+1)⌉.

When a binary tree with height h happens to have 2 h − 1 2^h - 1 2h − 1 element is called full binary tree. As shown in the figure:

The elements of the full binary tree with height h are numbered from the first layer to the last layer from left to right in each time, from 1 to 2 h − 1 2^h - 1 2h−1. Suppose k numbers are deleted from the full binary tree 2 h − i 2^h - i 2h − i element, 1 ≤ i ≤ k < 2 h 1 \le i \le k \lt 2^h 1 ≤ i ≤ K < 2h, the resulting binary tree is a complete binary tree. Full binary tree is a special case of complete binary tree. A complete binary tree with n elements, whose height is ⌈ l o g 2 ( n + 1 ) ⌉ \lceil log_2(n+1) \rceil ⌈log2​(n+1)⌉.

Feature 4 assumes that an element of a complete binary tree is numbered i, 1 ≤ i ≤ n 1 \le i \le n 1≤i≤n. The following relationships are established:
(1) If i = 1 i=1 If i=1, the element is the root of the binary tree. if i > 1 i \gt 1 i> 1, the number of its parent node is ⌊ i 2 ⌋ \lfloor \frac{i}{2} \rfloor ⌊2i​⌋.
(2) If 2 i > n 2i \gt n 2I > N, the element is not a child. Otherwise, the left child's number is 2 i 2i 2i.
(3) If 2 i + 1 > n 2i + 1 \gt n 2I + 1 > N, the element has no right child. Otherwise, the number of the right child is 2 i + 1 2i+1 2i+1.

3, Binary tree array description

The array representation of binary tree takes advantage of feature 4 and regards the binary tree as a complete binary tree without some elements, as shown in the figure (the dotted line is the missing part):

In the array representation, the elements of the binary tree are stored in the corresponding positions of the array according to their numbers. The array corresponding to the above figure is represented as:

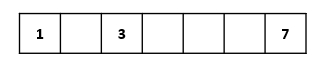
It can be seen that this representation is a waste of space when there are many missing elements. A binary tree with n elements may need at most 2 n 2^n 2n spaces to store. When each node other than the root node is the right child of its parent node, the storage space is wasted the most. This description is useful only when the number of missing elements is small

4, Binary tree interface

#pragma once
#include <functional>

template<typename T>
class binaryTree
{
public:
	virtual ~binaryTree() {}
	virtual bool empty() const = 0;
	virtual int size() const = 0;
	virtual void preOrder(std::function<void(T*)> visitFunc) = 0;
	virtual void inOrder(std::function<void(T*)> visitFunc) = 0;
	virtual void postOrder(std::function<void(T*)> visitFunc) = 0;
	virtual void levelOrder(std::function<void(T*)> visitFunc) = 0;
};

visitFunc provides the user with the function symbol to process each node in the traversal process.

5, Linked list implementation

1. Node class

#pragma once

template<typename T>
class binaryTreeNode
{
public:
	T element;
	binaryTreeNode* leftChild;
	binaryTreeNode* rightChild;

	binaryTreeNode(const T& element, binaryTreeNode* leftChild = nullptr, binaryTreeNode* rightChild = nullptr):
		element(element)
	{
		this->leftChild = leftChild;
		this->rightChild = rightChild;
	}
};

2. Interface

#pragma once
#include "binaryTree.h"
#include "binaryTreeNode.h"
#include <deque>

template<typename T>
class linkedBinaryTree : public binaryTree<T>
{
public:
	linkedBinaryTree();
	virtual ~linkedBinaryTree();
	linkedBinaryTree(const linkedBinaryTree& other);
	linkedBinaryTree(linkedBinaryTree&& other);
	linkedBinaryTree& operator=(const linkedBinaryTree& other);
	linkedBinaryTree& operator=(linkedBinaryTree&& other);
	
	virtual bool empty() const override;
	virtual int size() const override;
	virtual void preOrder(std::function<void(T)> visitFunc) override;
	virtual void inOrder(std::function<void(T)> visitFunc) override;
	virtual void postOrder(std::function<void(T)> visitFunc) override;
	virtual void levelOrder(std::function<void(T)> visitFunc) override;

	void makeTree(const T& element, linkedBinaryTree<T>&, linkedBinaryTree<T>&);
	int height();

private:
	binaryTreeNode<T>* root = nullptr;
	int treeSize = 0;
	std::function<void(T)> visitFunc;
	std::function<void(binaryTreeNode<T>*)> visitNodeFunc;

	void makeCopyAndSwap(const linkedBinaryTree& other);
	linkedBinaryTree makeCopy(const linkedBinaryTree& other);
	void copyChildNodes(binaryTreeNode<T>* src, binaryTreeNode<T>* dst);
	void swap(linkedBinaryTree& other);

	void preOrder(binaryTreeNode<T>* node);
	void inOrder(binaryTreeNode<T>* node);
	void postOrder(binaryTreeNode<T>* node);
	void levelOrder(binaryTreeNode<T>* node);
	void dealNodeVisit(binaryTreeNode<T>* node);	

	int height(binaryTreeNode<T>* node);
};

3. Copy constructor

Only destruct and internal copy interfaces are listed here:

template<typename T>
inline linkedBinaryTree<T>::~linkedBinaryTree()
{
	visitNodeFunc = [](binaryTreeNode<T>* node) {delete node; };
	postOrder(root);
	visitNodeFunc = std::function<void(binaryTreeNode<T>*)>();
}

template<typename T>
inline void linkedBinaryTree<T>::makeCopyAndSwap(const linkedBinaryTree& other)
{
	auto copyHashTable = makeCopy(other);
	swap(copyHashTable);
}

template<typename T>
inline linkedBinaryTree<T> linkedBinaryTree<T>::makeCopy(const linkedBinaryTree& other)
{
	linkedBinaryTree returnBinaryTree;

	returnBinaryTree.root = new binaryTreeNode<T>(other.root->element);
	returnBinaryTree.treeSize = other.treeSize;
	copyChildNodes(other.root, returnBinaryTree.root);

	return returnBinaryTree;
}

template<typename T>
inline void linkedBinaryTree<T>::copyChildNodes(binaryTreeNode<T>* src, binaryTreeNode<T>* dst)
{
	if (src->leftChild != nullptr)
	{
		dst->leftChild = new binaryTreeNode<T>(src->leftChild->element);
		copyChildNodes(src->leftChild, dst->leftChild);
	}

	if (src->rightChild != nullptr)
	{
		dst->rightChild = new binaryTreeNode<T>(src->rightChild->element);
		copyChildNodes(src->rightChild, dst->rightChild);
	}
}

template<typename T>
inline void linkedBinaryTree<T>::swap(linkedBinaryTree& other)
{
	using std::swap;
	swap(this->root, other.root);
	swap(this->treeSize, other.treeSize);
}

copyChildNodes is also a preorder traversal, except that the elements of the current node occur when called by the previous level. Only when the parent node is built can its left and right subtrees be constructed.

4. Traversal mode

There are four common ways to traverse binary trees: pre order traversal, middle order traversal, post order traversal and hierarchical traversal.

(1) Implementation of node / element processing function

The interface in the book is magical. Its traversal interface parameter is (void (*) (binarytree < T > *). This requires users to understand the node access method of the tree, which is obviously unreasonable. Therefore, we provide two member variables here, which are used to store the function of direct operation node (visitNodeFunc) and the function of direct operation element (visitffunc). The implementation of the real processing function is:

template<typename T>
inline void linkedBinaryTree<T>::dealNodeVisit(binaryTreeNode<T>* node)
{
	if (visitNodeFunc)
	{
		visitNodeFunc(node);
	}
	else if (visitFunc)
	{
		visitFunc(node->element);
	}
}

(2) Preorder traversal

The idea of preorder traversal is that for any input node,
① Access the current element;
② If there is a left child, deal with the left child;
③ If there is a right child, deal with the right child.
The processing here refers to recursively calling the preorder traversal function.

template<typename T>
inline void linkedBinaryTree<T>::preOrder(std::function<void(T)> visitFunc)
{
	this->visitFunc.swap(visitFunc);
	preOrder(root);
}

template<typename T>
inline void linkedBinaryTree<T>::preOrder(binaryTreeNode<T>* node)
{
	if (node == nullptr)
	{
		return;
	}

	dealNodeVisit(node);
	preOrder(node->leftChild);
	preOrder(node->rightChild);
}

(3) Medium order traversal

The idea of middle order traversal is: for any input node,
① If there is a left child, deal with the left child;
② Access the current element;
③ If there is a right child, deal with the right child.

template<typename T>
inline void linkedBinaryTree<T>::inOrder(std::function<void(T)> visitFunc)
{
	this->visitFunc.swap(visitFunc);
	inOrder(root);
}

template<typename T>
inline void linkedBinaryTree<T>::inOrder(binaryTreeNode<T>* node)
{
	if (node == nullptr)
	{
		return;
	}

	inOrder(node->leftChild);
	dealNodeVisit(node);
	inOrder(node->rightChild);
}

(4) Postorder traversal

The idea of post order traversal is: for any input node,
① If there is a left child, deal with the left child;
② If there is a right child, deal with the right child.
③ Access the current element;

template<typename T>
inline void linkedBinaryTree<T>::postOrder(std::function<void(T)> visitFunc)
{
	this->visitFunc.swap(visitFunc);
	postOrder(root);
}

template<typename T>
inline void linkedBinaryTree<T>::postOrder(binaryTreeNode<T>* node)
{
	if (node == nullptr)
	{
		return;
	}

	postOrder(node->leftChild);
	postOrder(node->rightChild);
	dealNodeVisit(node);
}

This is why we choose to use post order traversal to realize space release. Each time, the left and right subtrees are released first, and then themselves, which can ensure that all nodes are released.

(5) Hierarchical traversal

The idea of level traversal is to access the elements of the tree from top to bottom, from left to right. It is not difficult to see that we need to save all nodes with the help of queues. Why queues? Because the first node is processed, its child node should be added to the end of the container to ensure the processing order.

template<typename T>
inline void linkedBinaryTree<T>::levelOrder(std::function<void(T)> visitFunc)
{
	this->visitFunc.swap(visitFunc);
	levelOrder(root);
}

template<typename T>
inline void linkedBinaryTree<T>::levelOrder(binaryTreeNode<T>* node)
{
	std::deque<binaryTreeNode<T>*> queueNodesInSameLevel;

	while (node != nullptr)
	{
		dealNodeVisit(node);

		if (node->leftChild != nullptr)
		{
			queueNodesInSameLevel.push_back(node->leftChild);
		}

		if (node->rightChild != nullptr)
		{
			queueNodesInSameLevel.push_back(node->rightChild);
		}

		if (queueNodesInSameLevel.empty())
		{
			break;
		}

		node = queueNodesInSameLevel.front();
		queueNodesInSameLevel.pop_front();
	}
}

5. Construction tree

The tree is constructed from the root element and left and right subtrees:

template<typename T>
inline void linkedBinaryTree<T>::makeTree(const T& element, linkedBinaryTree<T>& left, linkedBinaryTree<T>& right)
{
	root = new binaryTreeNode<T>(element, left.root, right.root);
	treeSize = left.treeSize + right.treeSize + 1;

	// deny access from trees left and right
	left.root = right.root = nullptr;
	left.treeSize = right.treeSize = 0;
}

For simplicity, we don't use an R-value reference here, but its implementation is indeed mobile semantics.

6. Height

template<typename T>
inline int linkedBinaryTree<T>::height()
{
	return height(root);
}

template<typename T>
inline int linkedBinaryTree<T>::height(binaryTreeNode<T>* node)
{
	if (node == nullptr)
	{
		return 0;
	}

	int leftChildHeight = height(node->leftChild);
	int rightChildHeight = height(node->rightChild);

	return std::max(leftChildHeight, rightChildHeight) + 1;
}

7. Use

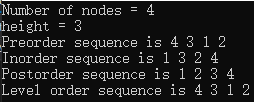
Simply changed the source code after the book:

// test linked binary tree class

#include <iostream>
#include "linkedBinaryTree.h"

using namespace std;

int test(void)
{
	linkedBinaryTree<int> a, x, y, z;
	y.makeTree(1, a, a);
	z.makeTree(2, a, a);
	x.makeTree(3, y, z);
	y.makeTree(4, x, a);

	cout << "Number of nodes = ";
	cout << y.size() << endl;

	cout << "height = ";
	cout << y.height() << endl;

	cout << "Preorder sequence is "; 
	y.preOrder([](int element) {cout << element << " "; });
	cout << endl;

	cout << "Inorder sequence is ";
	y.inOrder([](int element) {cout << element << " "; });
	cout << endl;

	cout << "Postorder sequence is ";
	y.postOrder([](int element) {cout << element << " "; });
	cout << endl;

	cout << "Level order sequence is ";
	y.levelOrder([](int element) {cout << element << " "; });
	cout << endl;

	return 0;
}