catalogue
1: Introduction to naive Bayes
1.1 classification method based on Bayesian decision theory
2.1 constructing word vector from text
2.2 calculating probability from word vector
2.3 modify the classifier according to the actual situation
3: Naive Bayesian filtering spam
1: Introduction to naive Bayes
Naive Bayesian method is a classification method based on Bayesian theorem and the assumption of feature conditional independence. For a given training set, firstly, the joint probability distribution of input and output is learned based on the independent assumption of characteristic conditions (the naive Bayes method, which obtains the model through learning, obviously belongs to the generative model); Then, based on this model, for a given input x, the output y with the maximum a posteriori probability is obtained by using Bayesian theorem.
1.1 classification method based on Bayesian decision theory
Firstly, for naive Bayes, its advantage is that it is still effective in the case of less data, and can deal with multi category problems. Its disadvantage is that it is more sensitive to the preparation of input data.
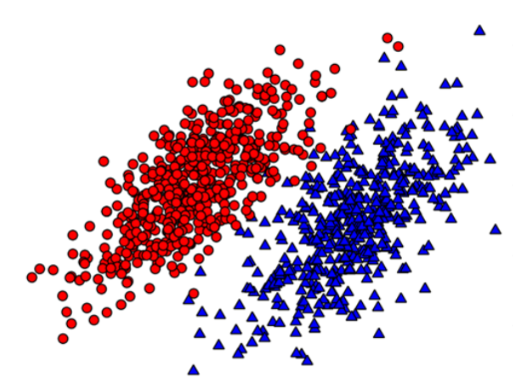
The idea of naive Bayes can be understood through the example in the figure below. Now we use p1(x,y) to represent the probability that the data point (x,y) belongs to category 1, that is, the dot in the figure below, and p2(x,y) to represent the probability that the data point (x,y) belongs to category 2, that is, the triangle in the figure below. Then we can use the following rules to judge its category:
If P1 (x, y) > P2 (x, y), the category is 1
If P2 (x, y) > P1 (x, y), the category is 2
That is to choose the category corresponding to high probability, which is the core idea of naive Bayes.
1.2 conditional probability
Conditional probability is the probability of event A under the condition that B is known to occur. We have also studied probability theory before, so we give the calculation formula directly here. The calculation formula of conditional probability is:
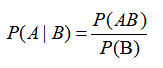
Another effective calculation method is Bayesian criterion, and the calculation formula is as follows:
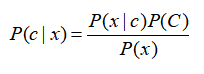
Now we use conditional probability to classify
According to the Bayesian decision theory proposed earlier, two probabilities p1(x,y) and p2(x,y) need to be calculated. Here is only a simplified description. P(C1|x,y) and P(C2|x,y) need to be calculated and compared. The meaning is that given a data point represented by X and y, the data site comes from the probability of category C1 and the probability of C2. The calculation formula here is
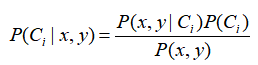
If P (c1|x, y) > P (c2|x, y), the category is 1; If P (c2|x, y) > P (c1|x, y), the category is 2
2: Document classification
2.1 constructing word vector from text
In document classification, the whole document is an instance, and some elements in e-mail constitute features. We can observe the words appearing in the document and take the appearance or absence of each word as a feature, so that the number of features will be as many as the items in the vocabulary. Naive Bayes is a common method for document classification
def loadDataSet():
postingList = [['my','dog','has','flea','problems','help','please'],
['maybe','not','take','him','to','dog','park','stupid'],
['my','dalmation','is','so','cute','I','love','him'],
['stop','posting','stupid','worthless','garbage'],
['mr','licks','ate','my','steak','how','to','stop','him'],
['quit','buying','worthless','dog','food','stupid']
]
classVec = [0,1,0,1,0,1]
return postingList,classVec
def createVocabList(dataSet):
vocabSet = set([])
for document in dataSet:
vocabSet = vocabSet | set(document)
return list(vocabSet)
def setOfWords2Vec(vocabList,inputSet):
returnVec = [0]*len(vocabList)
for word in inputSet:
if word in vocabList:
returnVec[vocabList.index(word)] = 1
else: print("this word:%s is not in my Vocabulary!" % word)
return returnVec
if __name__ == '__main__':
postingList,classVec = loadDataSet()
print("postingList:\n",postingList)
myVocabList = createVocabList(postingList)
print('myVocabList:\n',myVocabList)
trainMat = []
for postingLIst in postingList:
trainMat.append(setOfWords2Vec(myVocabList,postingLIst))
print('trainMat:\n',trainMat)The screenshot is not long enough to intercept the front part

2.2 calculating probability from word vector
Previously, we introduced how to convert a group of words into a group of numbers. The following is to calculate the probability according to these numbers.
def trainNBO(trainMatrix,trainCategory):
numTrainDocs = len(trainMatrix)
numWords = len(trainMatrix[0])
pAbusive = sum(trainCategory)/float(numTrainDocs)
p0Num = zeros(numWords); p1Num = zeros(numWords)
p0Denom = 0.0;p1Denom = 0.0
for i in range(numTrainDocs):
if trainCategory[i] ==1:
p1Num += trainMatrix[i]
p1Denom +=sum(trainMatrix[i])
else:
p0Num += trainMatrix[i]
p0Denom += sum(trainMatrix[i])
p1Vect = p1Num/p1Denom
p0Vect = p0Num/p0Denom
return p0Vect,p1Vect,pAbusive
if __name__ == '__main__':
postingList,classVec = loadDataSet()
myVocabList = createVocabList(postingList)
trainMat = []
for postingLIst in postingList:
trainMat.append(setOfWords2Vec(myVocabList,postingLIst))
p0V,p1V,pAb = trainNBO(trainMat,classVec)
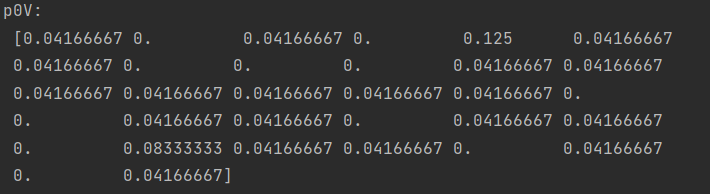
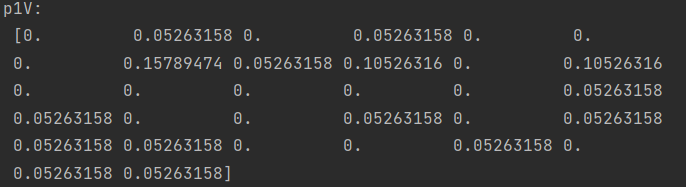
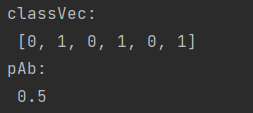
print('p0V:\n',p0V)
print('p1V:\n', p1V)
print('classVec:\n', classVec)
print('pAb:\n', pAb)
2.3 modify the classifier according to the actual situation
When using Bayesian classifier to classify documents, it is necessary to calculate the product of multiple probabilities. Once the probability that the document belongs to a certain type is obtained, that is, calculate p(w0|1),p(w1|1),p(w2|1). If one probability is 0, the final product will be 0. In order to reduce this impact, the occurrence times of all words can be initialized to 1 and the denominator can be initialized to 2
Then there is the underflow problem. Due to the multiplication of too many small numbers, the program may overflow or fail to get the correct answer. This problem can be solved by logarithmic multiplication. The modification is as follows:
p0Num = ones(numWords); p1Num = ones(numWords) p0Denom = 2.0;p1Denom = 2.0 p1Vect = log(p1Num/p1Denom) p0Vect = log(p0Num/p0Denom)
Then you can complete the classifier well
def classifyNB(vec2Classify,p0Vec,p1Vec,pClass1):
p1 = sum(vec2Classify*p1Vec)+log(pClass1)
p0 = sum(vec2Classify*p0Vec)+log(1.0-pClass1)
if p1>p0:
return 1
else:
return 0
def testingNB():
listOPosts,listClasses = loadDataSet()
myVocabList = createVocabList(listOPosts)
trainMat = []
for posinDoc in listOPosts:
trainMat.append(setOfWords2Vec(myVocabList,posinDoc))
p0V,p1V,pAb = trainNBO(array(trainMat),array(listClasses))
testEntry = ['love','my','dalmation']
thisDoc = array(setOfWords2Vec(myVocabList,testEntry))
if classifyNB(thisDoc,p0V,p1V,pAb):
print(testEntry,'It belongs to the insult category')
else:
print(testEntry,'It belongs to the non insulting category')
testEntry = ['stupid','garbage']
thisDoc = array(setOfWords2Vec(myVocabList,testEntry))
if classifyNB(thisDoc,p0V,p1V,pAb):
print(testEntry, 'It belongs to the insult category')
else:
print(testEntry, 'It belongs to the non insulting category')

2.4 document word bag model
So far, we take the occurrence of each word as a feature, which can be described as a word set model. If a word appears in the document more than once, it may mean that it contains some information that cannot be expressed by whether the word appears in the document. This method is called document word bag model.
def bagOfWords2VecMN(vocabList,inputSet):
returnVec = [0]*len[vocabList]
for word in inputSet:
if word in vocabList:
returnVec[vocabList.index(word)] +=1
return returnVec
3: Naive Bayesian filtering spam
import numpy as np
import random
import re
def createVocabList(dataSet):
vocabSet = set([])
for document in dataSet:
vocabSet = vocabSet | set(document)
return list(vocabSet)
def setOfWords2Vec(vocabList,inputSet):
returnVec = [0]*len(vocabList)
for word in inputSet:
if word in vocabList:
returnVec[vocabList.index(word)] = 1
else: print("this word:%s is not in my Vocabulary!" % word)
return returnVec
def trainNBO(trainMatrix,trainCategory):
numTrainDocs = len(trainMatrix)
numWords = len(trainMatrix[0])
pAbusive = sum(trainCategory)/float(numTrainDocs)
p0Num = ones(numWords); p1Num = ones(numWords)
p0Denom = 2.0;p1Denom = 2.0
for i in range(numTrainDocs):
if trainCategory[i] ==1:
p1Num += trainMatrix[i]
p1Denom +=sum(trainMatrix[i])
else:
p0Num += trainMatrix[i]
p0Denom += sum(trainMatrix[i])
p1Vect = log(p1Num/p1Denom)
p0Vect = log(p0Num/p0Denom)
return p0Vect,p1Vect,pAbusive
def classifyNB(vec2Classify,p0Vec,p1Vec,pClass1):
p1 = sum(vec2Classify*p1Vec)+log(pClass1)
p0 = sum(vec2Classify*p0Vec)+log(1.0-pClass1)
if p1>p0:
return 1
else:
return 0
def textParse(bigString):
listOfTokens = re.split(r'\W+',bigString)
return [tok.lower() for tok in listOfTokens if len(tok) >2]
def spamTest():
docList = [];classList = []; fullText = []
for i in range(1,26):
wordList = textParse(open('email/spam/%d.txt' % i, 'r').read())
docList.append(wordList)
fullText.append(wordList)
classList.append(1)
wordList = textParse(open('./email/ham/%d.txt' % i, 'r').read())
docList.append(wordList)
fullText.append(wordList)
classList.append(0)
vocabList = createVocabList(docList)
trainingSet = list(range(50));testSet = []
for i in range(10):
randIndex = int(random.uniform(0, len(trainingSet)))
testSet.append(trainingSet[randIndex])
del (trainingSet[randIndex])
trainMat = [];
trainClasses = []
for docIndex in trainingSet:
trainMat.append(setOfWords2Vec(vocabList, docList[docIndex]))
trainClasses.append(classList[docIndex])
p0V, p1V, pSpam = trainNBO(np.array(trainMat), np.array(trainClasses))
errorCount = 0
for docIndex in testSet:
wordVector = setOfWords2Vec(vocabList, docList[docIndex])
if classifyNB(np.array(wordVector), p0V, p1V, pSpam) != classList[docIndex]:
errorCount += 1
print("Misclassified test sets:", docList[docIndex])
print('the error rate is:'(float(errorCount) / len(testSet) * 100))
if __name__ == '__main__':
spamTest()