📢 Blog home page: 🏀 Bryant typing the code🏀
📢 Welcome to praise 👍 Collection ⭐ Leaving a message. 📝 Welcome to discuss! 👏
📢 This article was originally written by [Bryant who knocked the code], and was first launched in CSDN 🙉🙉🙉
📢 Since the blogger is learning Xiaobai, there will inevitably be mistakes. If you have any questions, please leave a message in the comment area. Thank you very much! ✨
📖 Boutique column (updated from time to time)[ JavaSE] [Java data structure][LeetCode]

Preorder traversal of binary tree

As like as two peas, the same way is to change the access order of the nodes, and the code is exactly the same, but in order of order.

Title:

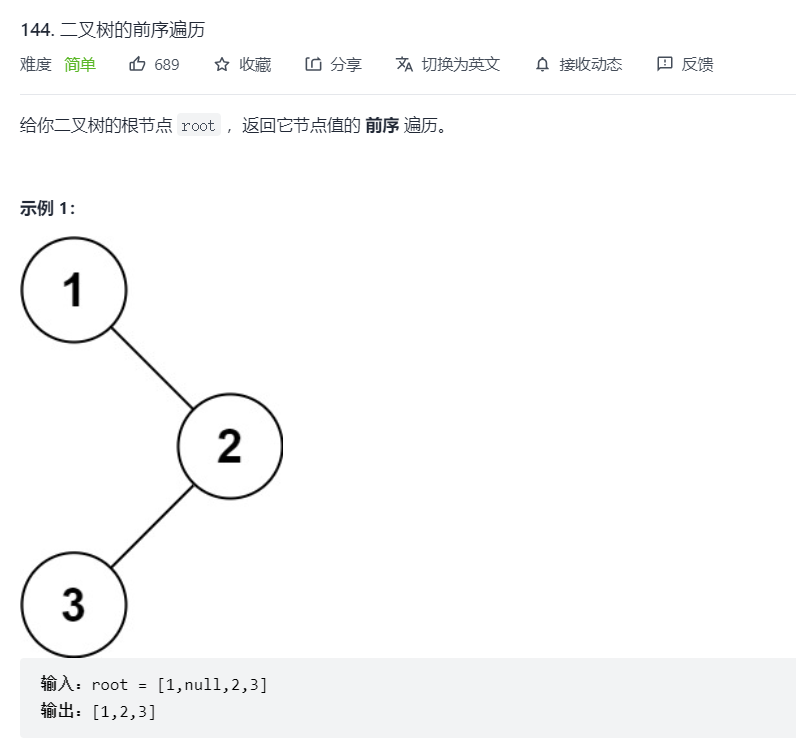
Idea: this question requires that the traversed nodes be put into a List and returned

1. Preorder traversal order: root node - > left child node - > right child node
2. Judge the root node first. If the root node is empty, return list directly
3. Store the currently accessed root node in the sequence table
4. Then recursively access the left child node
5. Finally, the right child node is accessed recursively

Implementation code:

class Solution {
    List<Integer> list = new ArrayList<>();
    public List<Integer> preorderTraversal(TreeNode root) {
        if(root==null){//Root node empty
            return list;//Direct return sequence table
        }
        list.add(root.val);//Store the value of the currently accessed root node in the sequence table
        preorderTraversal(root.left);//Access left node
        preorderTraversal(root.right);//Access right node
        return list;
    }
}

Medium order traversal

Title:

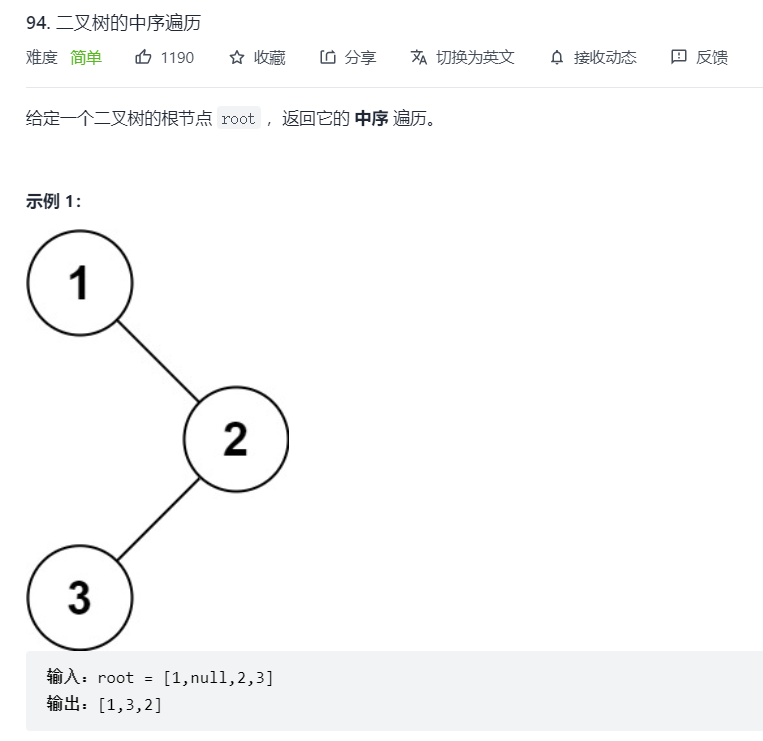
Idea: this question requires that the traversed nodes be put into a List and returned

1. Middle order traversal order: left child node - > root node - > right child node
2. First judge the current root node. If the root node is empty, directly return to list
3. Access left child node
4. Store the currently accessed root node value in the sequence table
5. Finally, access the right child node

Implementation code:

class Solution {
    List<Integer> list = new ArrayList<>();
    public List<Integer> inorderTraversal(TreeNode root) {
        if(root==null){//Judge whether the current root node is empty
            return list;
        }
        inorderTraversal(root.left);//Access left child node
        list.add(root.val);//Store the value of the currently accessed root node in the sequence table
        inorderTraversal(root.right);//Access the right child node
        return list;
    }
}

Subsequent traversal

Title: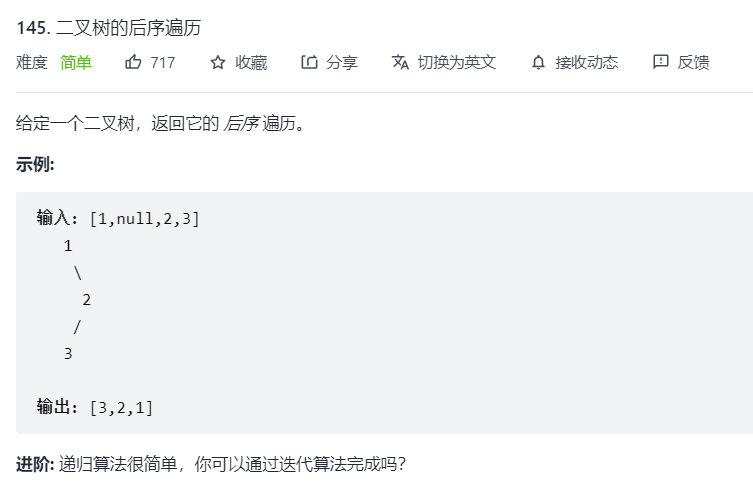

Idea: this question requires that the traversed nodes be put into a List and returned

1. Post order traversal order: left child node - > right child node - > root node
2. First judge the current root node. If the root node is empty, directly return to list
3. Access left child node
4. Access the right child node
5. Finally, the currently accessed root node value is stored in the sequence table

Implementation code:

class Solution {
    List<Integer> list = new ArrayList<>();
    public List<Integer> postorderTraversal(TreeNode root) {
         if(root==null){//Judge whether the root node is empty
            return list;
        }
        postorderTraversal(root.left);//Access left child node
        postorderTraversal(root.right);//Access the right child node
        list.add(root.val);//Store the value of the currently accessed root node in the sequence table
        return list;
    }
}

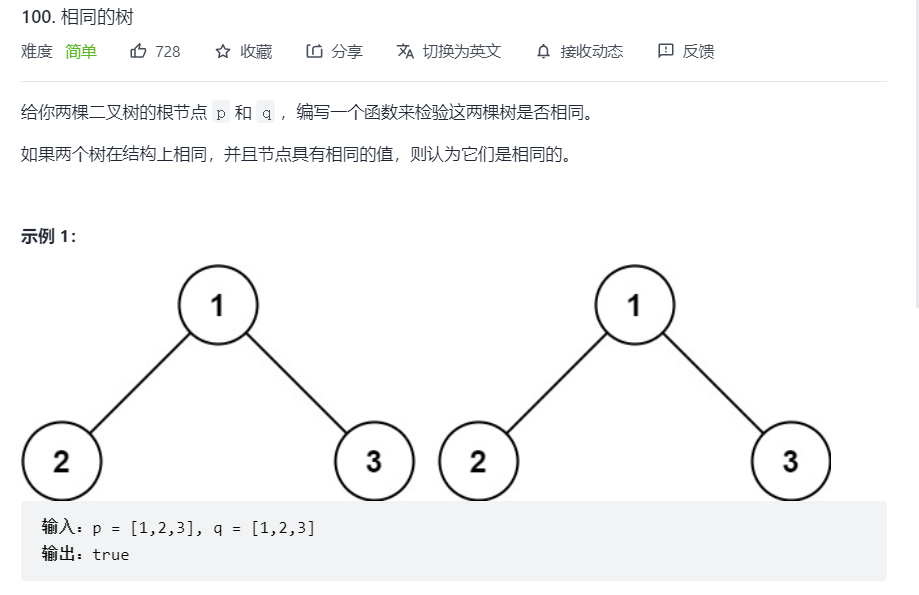
Judge whether the two trees are the same

Title:

Idea:

1. First, make sure that the two trees are the same, which means that the left subtree and the right subtree are the same, and the values are the same
2. First, judge whether the root nodes of the two trees are empty. If the root nodes of the two trees are empty, the two trees are the same and return true directly;
3. If only the root node of one tree is empty and the root node of the other tree is not empty, the two trees must be different and return false directly
4. If the root nodes of the two trees are not empty, compare their values. If the values are different, the two trees are different and return false
5. When the above conditions do not return false, that is, the root nodes of the two trees are the same, then use recursion to judge whether their left and right child nodes are the same, and carry out dolly

Implementation code:

class Solution {
    public boolean isSameTree(TreeNode p, TreeNode q) {
        //Both are empty
        if(p == null && q == null) {
            return true;
        }
        //Only one is not empty
        if(p == null || q == null) {
            return false;
        }
        //None is empty
        if(p.val != q.val) {
            return false;
        }
        //If p and q are not empty and the corresponding values are the same, judge the left and right trees of the two trees
        return isSameTree(p.left,q.left) && isSameTree(p.right,q.right);
    }
}

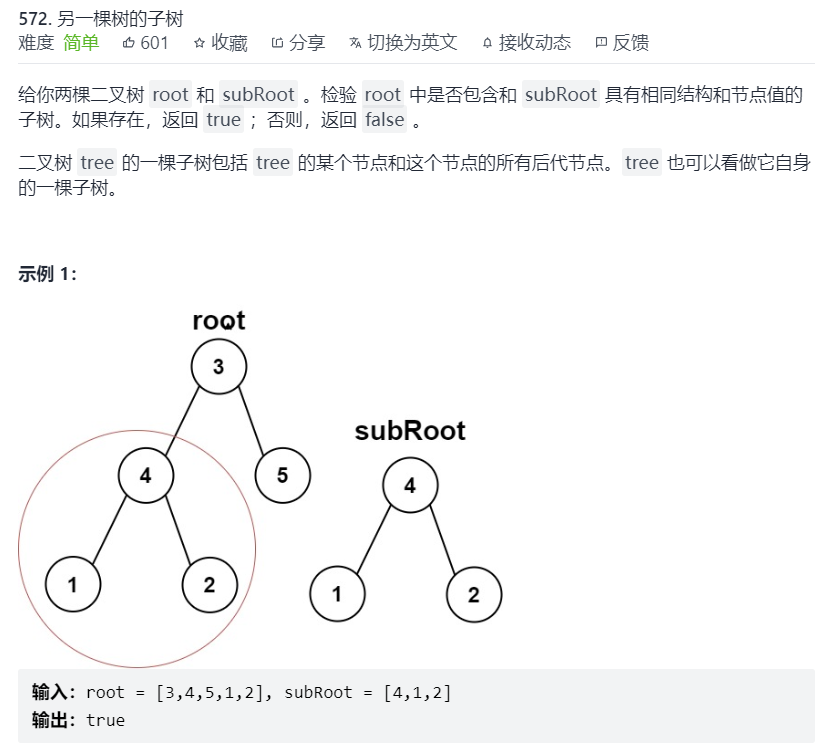
Is the other tree a subtree of the current tree

Title:

Idea:

1. This problem requires as like as two peas of the same tree, which is the same as the last one.
2. If the root node of the current tree is empty, the other tree must not be its subtree
3. If the root node of another tree is empty, it must be a subtree of the current tree
4. Every time a node recurses down, it is necessary to judge whether the tree represented by the current root node is the same as another tree
   

Implementation code:

class Solution {
    public boolean isSubtree(TreeNode root, TreeNode subRoot) {
        if (subRoot == null) return true; //If the root node of another tree is empty, it must be a subtree of the current tree
        if (root == null) return false; //If the root node of the current tree is empty, the other tree must not be its subtree
        return isSubtree(root.left,subRoot)||isSubtree(root.right,subRoot)||isSameTree(root,subRoot);//Before going down a node, it is necessary to judge whether the tree represented by the current root node is the same as another tree
    }
    
     public boolean isSameTree(TreeNode s, TreeNode t) {
        if (s == null && t == null) return true;//All empty
        if (s == null || t == null) return false;//One is not empty
        if(s.val!=t.val) return false;//If the values are different, false is returned
        //If the values are the same, continue to judge the next node
        return isSameTree(s.left, t.left) && isSameTree(s.right, t.right);
    }
}

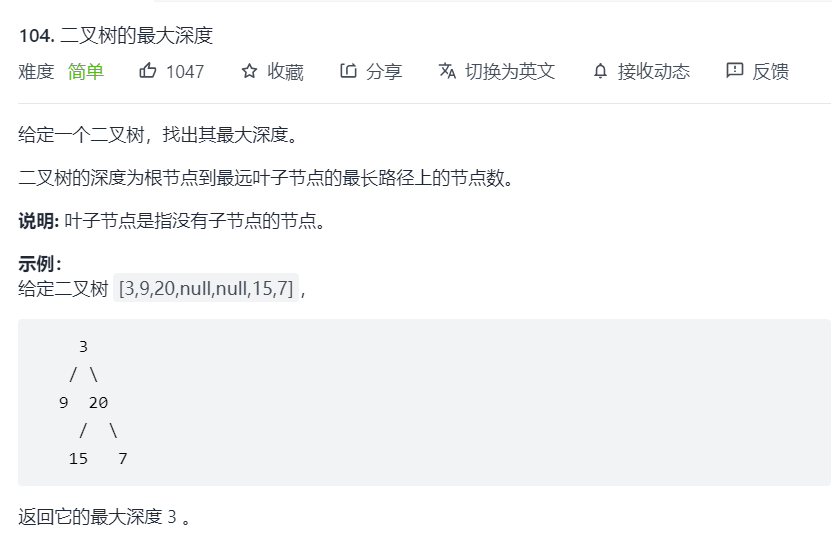
Find the maximum depth of binary tree

Title:

Idea:

1. First understand a problem, that is, the depth of the binary tree = the depth of the left subtree and the depth of the right subtree, whichever is greater
2. So there is a formula, maximum depth = left subtree depth > right subtree depth? Left subtree depth: right subtree depth
3. Using the formula, recursion can be carried out
4. First judge whether the current root node is empty. If it is empty, it returns 0 (i.e. the depth is 0)
5. Then judge the depth of the left subtree and the right subtree in turn
6. Note: when returning, it should be + 1, because the root node is also a layer
   

Implementation code:

class Solution {
    public int maxDepth(TreeNode root) {
        if(root==null){//If the root node is empty, 0 is returned
            return 0;
        }
        int a=maxDepth(root.left);//Find the height of the left subtree
        int b=maxDepth(root.right);//Find the height of the right subtree
        return (a > b ? a : b )+ 1;//Recursive formula
    }
}

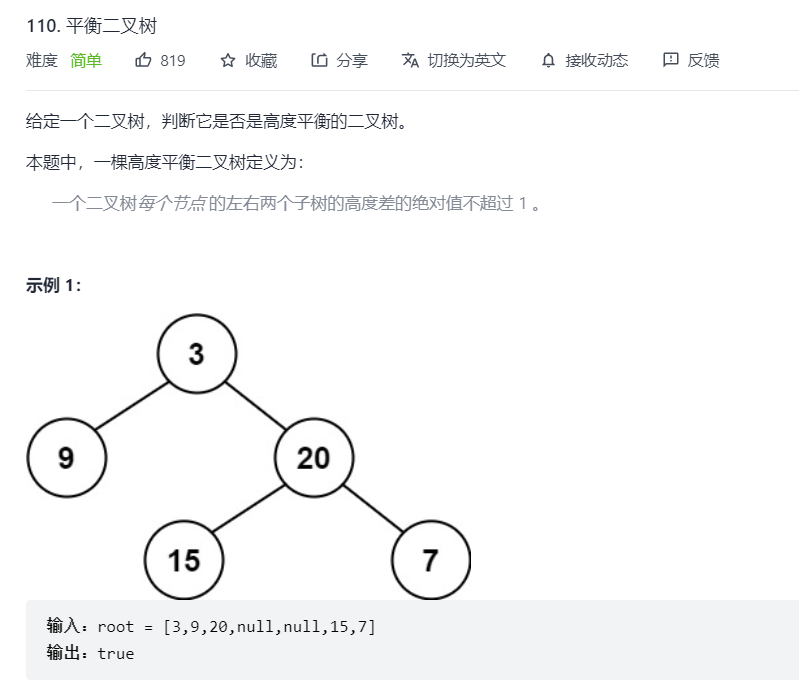
Judge whether the binary tree is a balanced binary tree

Title:

Idea:

1. In this question, a highly balanced binary tree is defined as:
   The absolute value of the height difference between the left and right subtrees of each node of a binary tree does not exceed 1.
2. Take the idea of looking from bottom to top and write an additional method to judge the height of the tree
3. Judge whether the absolute value of the difference between the left subtree height and the right subtree height of the current root node does not exceed 1
4. If the balance condition is met, the subtree height is returned; otherwise, the subtree height is returned

Implementation code:

class Solution {
    public boolean isBalanced(TreeNode root) {
        if(height(root)>=0)
            return true;
        else 
            return false;
    }
    //Look from bottom to top
    public int height(TreeNode root) {
        if (root == null) //The root node is empty and returns 0
        return 0;
        
        int left = height(root.left);//Get left node height
        if(left == -1) 
        return -1;
        
        int right = height(root.right);//Get right node height
        if(right == -1) 
        return -1;
        
        return Math.abs(left - right) <=2 ? Math.max(left, right) + 1 : -1;
        //If the absolute value of the height difference between the left subtree and the right subtree is not greater than 1, the height of the subtree is returned; otherwise, - 1 is returned
    }
}

Judge mirror binary tree

Title:

Idea:

1. In fact, this problem is to judge whether the left and right subtrees are the same, but a little change needs to be made
2. To judge whether it is a mirror image, the change is that the left child value of the left subtree should be equal to the right child value of the right subtree, and the right child value of the left subtree should be equal to the left child value of the right subtree
   

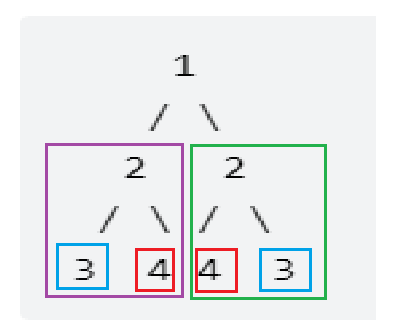
Implementation code:

class Solution {
    public boolean isSymmetric(TreeNode root) {
        if(root==null){
            return false;  
        }
        return isSame(root.left,root.right);//If the left and right subtrees meet the mirror condition, they are mirror binary trees
    }
    
    public boolean isSame(TreeNode a,TreeNode b){
        
        if(a == null && b ==null)
            return true;
        
        if(a == null || b ==null)
            return false;
        
        if(a.val != b.val)
            return false;
        
        //The key is the last line of code
        //The left child value of the left subtree should be equal to the right child value of the right subtree
        //The right child value of the left subtree should be equal to the left child value of the right subtree
        return isSame(a.left,b.right)&&isSame(a.right,b.left);
    }
}

🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙
        ❤ Originality is not easy. If there is any error, please leave a message in the comment area. Thank you very much ❤
        ❤                 If you think the content is good, it's not too much to give a three company~        ❤
        ❤                              I'll pay a return visit when I see it~                                      ❤
🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙🌙