I Red black tree:
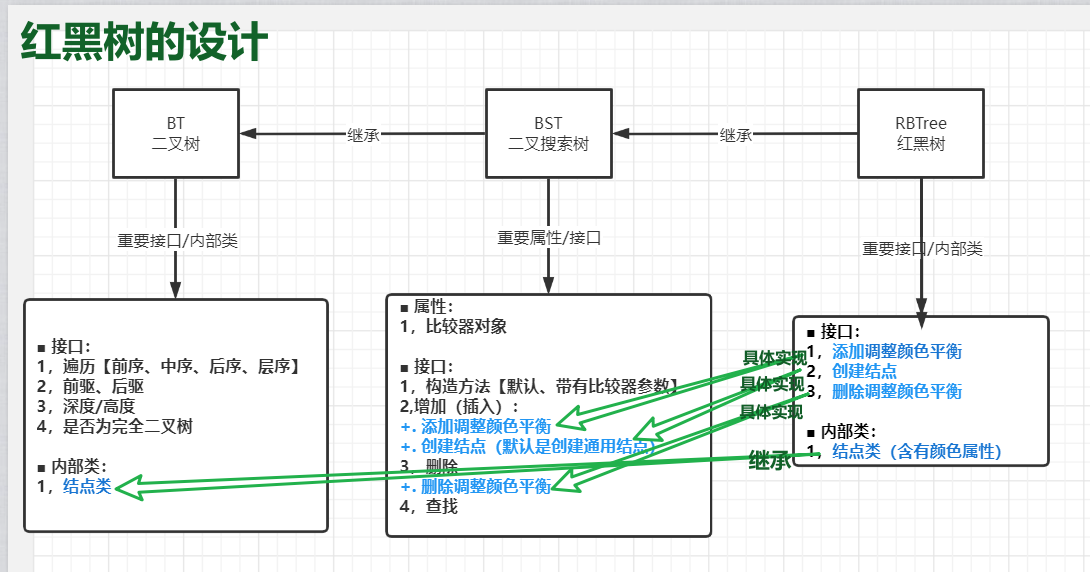
☼ Introduction to red black tree:
-----------Morphologically, it is a special binary search tree [specially reflected in color, and logically, it is equivalent to a fourth-order B tree]
❀ how is a red black tree equivalent to a fourth-order B tree? --------- To turn the red black tree into a B-tree: you need to merge the red node and the black node (black is the root [also the intermediate element]).
✿ Red black -- > b tree: there are four types of nodes: ① red black red, ② red black, ③ black red and ④ black
❀ common interface of red black tree:
General interface of binary search tree+ After adding, deleting
Rotate left and right, and update parent node relationship after rotation (the same as AVL tree after rotation and rotation)
■ all positions inserted:

■ after addition:
❀ summarize the adjustment after adding the red black tree ❀:1. Classification: (the specific process needs to be symmetrical according to the parent node as the left node and the right node) (1) No adjustment required:■ the current node is the root and can be dyed black; ■ the parent node is black and does not need to be processed. (2) Need to adjust: (divided according to whether the uncle node is red)■ case1: the uncle is red, and the current node x can be left or right. Dye the black father, uncle, dye the red master, and trace back to the node master. ■ case2: the uncle is black, and the current node x is the right child [red is LR type]. First rotate left and convert to case3; (first consider that the current node is a right child, because it will become case3 after processing) [small details, when the current node x points to the parent node, rotate x (in fact, the position of the original parent node is rotated)];■ case3: the uncle is black, the current node x is the left child [red is LL type], dye the black father, dye the red master, and then turn right. |
@Override
protected void afterAdd(Node<E> node) {
// Judge parent node
Node<E> parent = node.parent;
// The root node is added [when adding the first node] / or overflows to the root node
if (parent == null) {
black(node);
return;
}
// If the parent node is black, it does not need to be processed and returns directly
if (isBlack(parent))
return;
// If the uncle node is red [overflow of B tree]
Node<E> uncle = parent.sibling();
Node<E> grand = red(parent.parent);
if (isRed(uncle)) {
// Dye black father and uncle, dye grandfather red, which is equivalent to the newly inserted node
black(uncle);
black(parent);
// ① When overflow occurs, it should also be dyed red
afterAdd(grand);
return;
}
// Take a look, optimize the code, extract the jointly owned from the outside, and so on
// Come here, uncle is not red
if (parent.isLeftChild()) { // L
// ② When rotating, you should also dye the nodes red
if (node.isLeftChild()) { // LL
// Dye black parent node, dye red grandfather node
black(parent);
// Dextral
} else { // LR
// Dye yourself red and dye yourself black
black(node);
// Left back right rotation
rotateLeft(parent);
}
rotateRight(grand);
} else { // R
// ② When rotating, you should also dye the nodes red
if (node.isLeftChild()) { // RL
// Dye yourself red and dye yourself black
black(node);
// Left back right rotation
rotateRight(parent);
} else { // RR
// Dye black parent node, dye red grandfather node
black(parent);
// Sinistral
}
rotateLeft(grand);
}
}■ all positions deleted: (the picture is from xiaomaige Education)
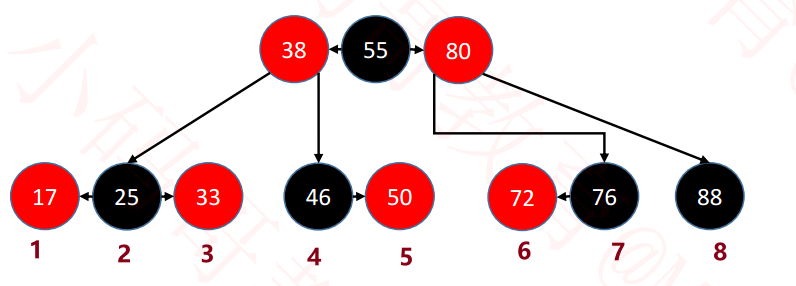
■ after deletion:
❀ summarize the adjustment after deleting the red black tree ❀:1. The deleted node is red (perfect) and does not need to be processed; 2. The deleted node is black: [look at the replacement node - front / rear drive node] (1) The replacement node is red, and the replacement node is dyed black [predecessor / follower node] (2) The alternative node is black (if it is a root, it is perfect and does not need to be processed). Black node: ● black leaf node: [look at brother]:----- From the perspective of B tree, underflow occurred [for processing in the B tree, borrow from brothers. If brothers can't borrow, find the parent node and merge] [1] Brothers are black and can borrow (at least one sub red node). Rotate to borrow. [if you borrow directly, it does not meet the characteristics of binary search tree. The root is larger than the left subtree and smaller than the right subtree (you need to rotate and exchange nodes, (meet the characteristics of binary search tree) and then borrow again)]. [2] Brothers are black and cannot be borrowed (there is no red node). See the parent node: ① The parent node is red: the parent node is dyed black and the brother is dyed red to merge. ② The parent node is black and underflow is processed. [3] Brothers are red. By rotating, nephews (black nodes) become brothers [and brothers of deleted nodes are black nodes] |
● black leaf node: [look at brother]:
[3] Brother is red. By rotating, the nephew (black node) becomes brother [and the brother node of the deleted node is black node]:
It can only be illustrated: (brother and parent nodes are on the same child node (on the same layer) of the B-tree, and the red brother has two black child nodes) (the picture is from xiaomaige Education)
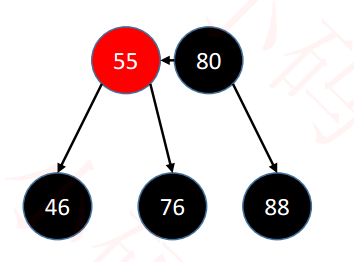
❀ When deleting the black leaf node, underflow occurs, and obviously brothers who are not on the same layer must not lend the node,
You can only consider being on the same level as yourself [brother's son] and borrowing from brother's son. [but the premise of borrowing in the B tree is that the two are brothers] so the goal is to turn my brother's son into my brother in order to borrow smoothly.
[2] Brothers are black and cannot be borrowed (there is no red node). See the parent node:
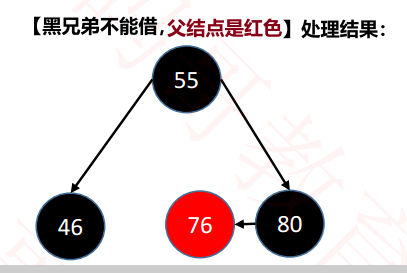
① The parent node is red: the parent node is dyed black and the brother is dyed red to merge. (picture from xiaomaige Education)
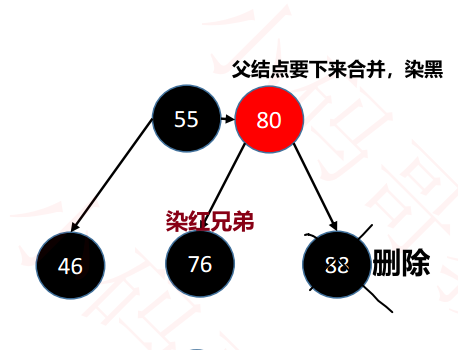
(picture from xiaomaige Education)
[2] Brothers are black and cannot be borrowed (there is no red node). See the parent node:
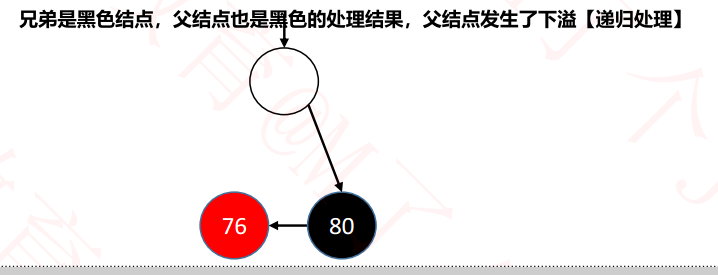
② The parent node is black and underflow is processed.
(picture from xiaomaige Education)
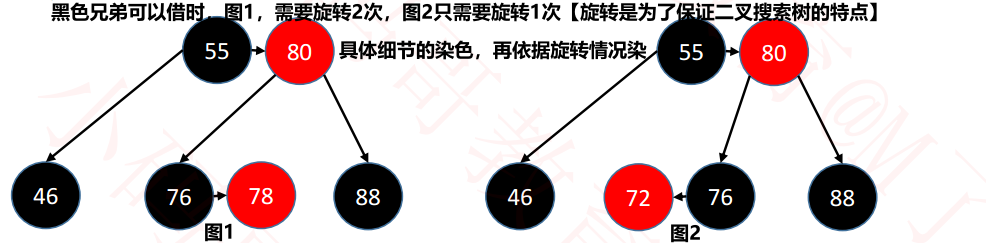
[1] Brothers are black and can borrow (at least one sub red node). Rotate to borrow. [the result of rotation is that it becomes a root (an independent B-tree node), so it needs to be dyed black]
[if you borrow directly, it does not meet the characteristics of binary search tree. The root is larger than the left subtree and smaller than the right subtree (you need to rotate and exchange nodes, (meet the characteristics of binary search tree) and then borrow again)]. (picture from xiaomaige Education)
protected void afterRemove2(Node<E> node, Node<E> replacement) {
//The deleted node is red or the substitute node [predecessor / successor] is red
if(isRed(node)) return;
if (isRed(replacement)) {
black(replacement);
return;
}
//Next, consider deleting nodes in black [excluding roots]
Node<E> parent = node.parent;
// The root node is deleted
if (parent == null)
return;
// Delete the black leaf node underflow
boolean left = parent.left == null || node.isLeftChild();// Judge whether the deleted node is left or right
Node<E> sibling = left ? parent.right : parent.left;
if (left) { // The deleted node is on the left and the sibling node is on the right
//Look at brothers [brothers are red, dyed black brothers, let brothers become roots through left rotation, update brother position]
if (isRed(sibling)) { // The sibling node is red
black(sibling);
red(parent);
rotateLeft(parent);
// Re point to brother (update brother position)
sibling = parent.right;
}
// [brother node is black, brother has no red sub node, can't borrow] ~ underflow
if (isBlack(sibling.left) && isBlack(sibling.right)) {
// If the sibling node cannot be lent out, the parent node should merge with the sibling node downward [the parent node is the root of the next node]
boolean parentBlack = isBlack(parent);
black(parent);
red(sibling);
if (parentBlack) {//If the parent node is black, it will collapse and recursion
afterRemove2(parent, null);
}
// [brother nodes are black, and brothers have red sub nodes that can be borrowed]
} else {
// The left node of the sibling node is black. The sibling must rotate first
if (isBlack(sibling.right)) {
rotateRight(sibling);
//Update brother node
sibling = parent.right;
}
//After rotation, the rotated central node inherits the color of the parent;
//The left and right nodes after rotation are dyed as BLACK - [become independent B-tree nodes]
color(sibling, colorOf(parent));
black(sibling.right);
black(parent);
rotateLeft(parent);
}
} else { // The deleted node is on the right and the sibling node is on the left
if (isRed(sibling)) { // The sibling node is red
black(sibling);
red(parent);
rotateRight(parent);
// Change brothers
sibling = parent.left;
}
// Brother nodes must be black
if (isBlack(sibling.left) && isBlack(sibling.right)) {
// The sibling node does not have a red child node. The parent node should merge with the sibling node
boolean parentBlack = isBlack(parent);
black(parent);
red(sibling);
if (parentBlack) {
afterRemove2(parent,null);
}
} else { // The sibling node has at least one red sub node and borrows elements from the sibling node
// The left side of the brother node is black. Brothers should rotate first
if (isBlack(sibling.left)) {
rotateLeft(sibling);
sibling = parent.left;
}
color(sibling, colorOf(parent));
black(sibling.left);
black(parent);
rotateRight(parent);
}
}
} https://www.cnblogs.com/shan333/p/15496806.html
https://www.cnblogs.com/shan333/p/15496806.html