@TOC
Overview of common sorting algorithms
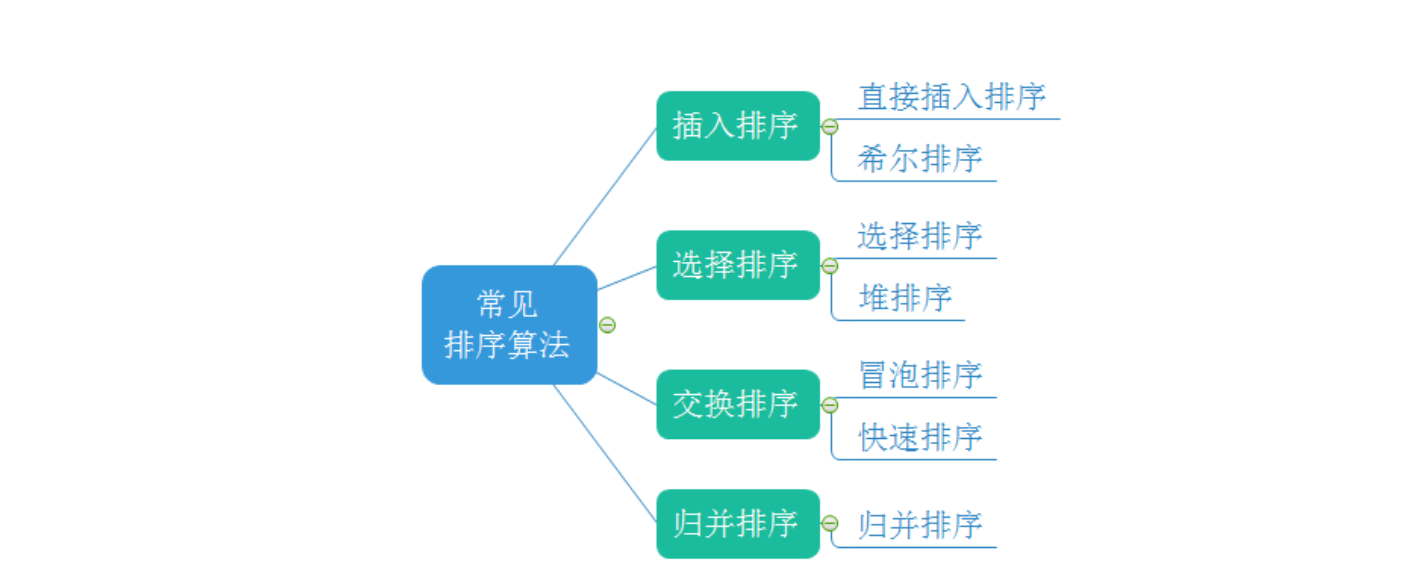
1. Concept
1.1 sorting
Sorting is the operation of increasing or decreasing the sequence to be sorted according to the size of one or some keywords (what is used as the benchmark). If sorting is mentioned at ordinary times, it usually refers to ascending (non descending) order. Sorting in the general sense refers to in place sort.
1.2 stability (important)
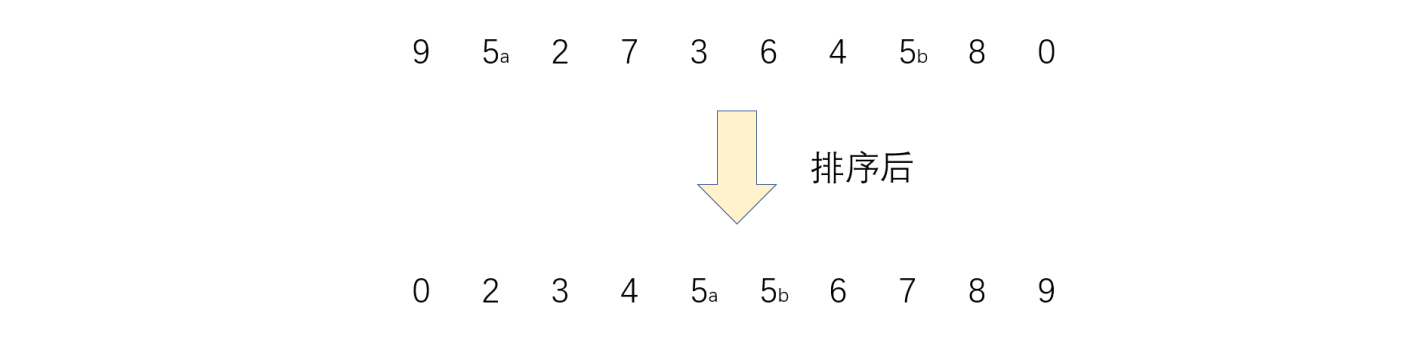
If the sorting algorithm can ensure that the relative position of two equal data does not change after sorting, we call the algorithm a stable sorting algorithm. For example, the algorithm for sorting the following sequence is a stable sorting algorithm.
Sorting is widely used. Sorting can be used as long as it involves comparison, selection, etc.
2. Insert sort
2.1 direct insertion sort - principle
As a whole interval, the sequence to be sorted is divided into ordered interval and unordered interval, * * first, the first element of the sequence to be sorted itself is ordered. It is used as an ordered interval alone, and the element behind the first element is used as an unordered interval. Each time, select the first element of the unordered interval and insert it at an appropriate position in the ordered interval, Until all elements in the unordered interval are inserted into the ordered interval** The general idea is like this. I'll draw a picture below and take an example to see some detailed processes.
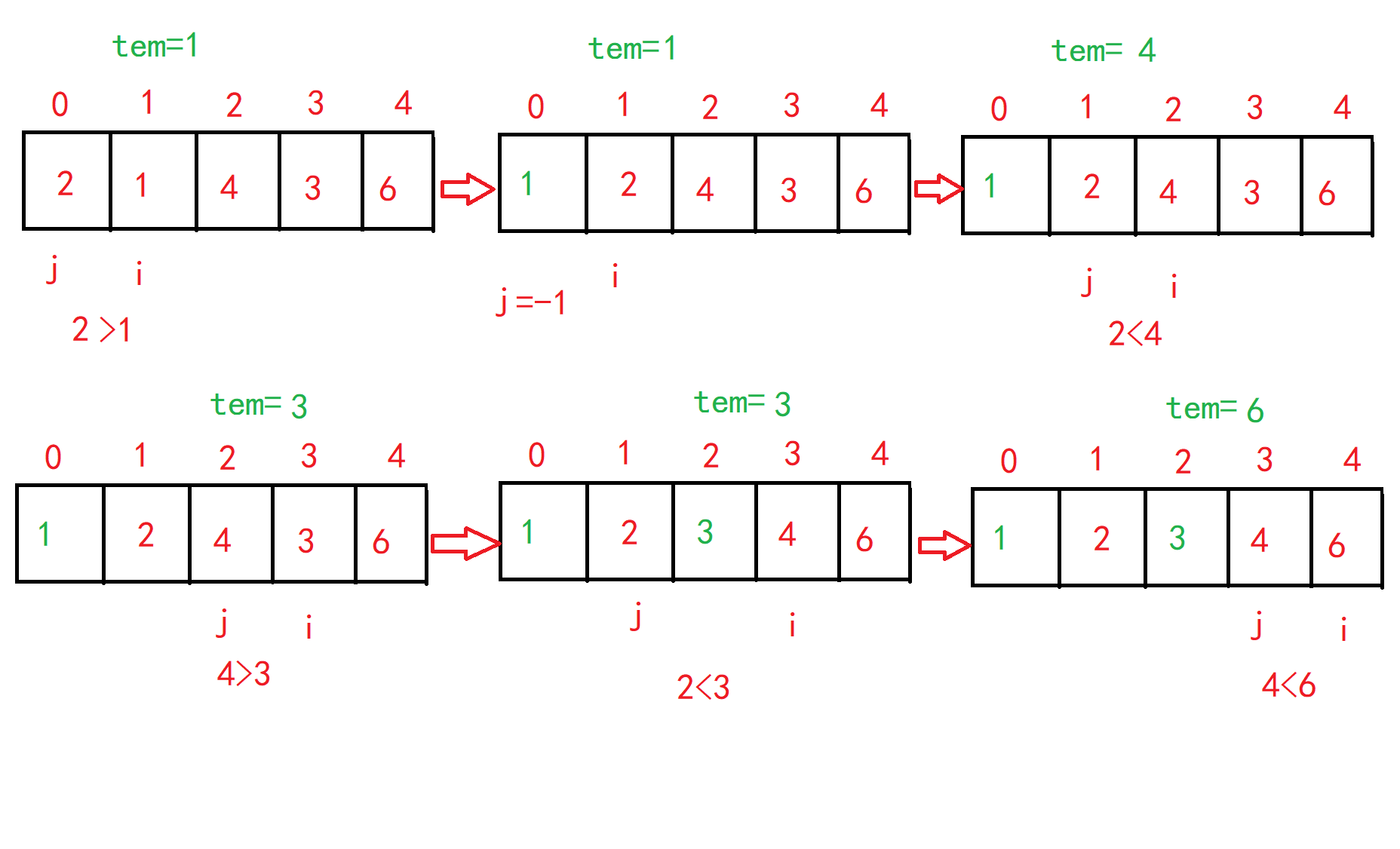
Suppose that the array elements 2, 1, 4, 3 and 6 are arranged in ascending order. Firstly, the variable i traverses the array forward from the subscript 1 to the first element of the unordered area. Each time, the variable j traverses the array backward from the last position of i, and puts the value of position i into a temporary variable TEM. When the value of position j is greater than the value of TEM, move the value of position j forward to position i to expand the size of the ordered area, After that, j continues to move to find the appropriate position where tem is placed in the ordered area, and compare it with the value of i position. If the element at j position is still larger than that at i position, continue to move until j is negative or find an element pointed by j smaller than that pointed by i. At this time, the value of i can be placed in the appropriate position of the ordered area. The key code at this time is array[j + 1] = tem;
2.2 code implementation
public static void insertSort(int[] array) {
if(array==null) return;
for (int i = 1; i < array.length; i++) {
int j = i - 1;
int tem = array[i];
while (j >= 0) {
if (array[j] > tem) {
array[j+1] = array[j];
j--;
//i--;
} else {
break;
}
}
array[j + 1] = tem;
}
}
2.3 performance analysis
Time complexity:
Best: O(n). When the data is in order, you only traverse the array once. Worst: O(n^2). When the data is in reverse order, you should both traverse the array and compare the array. The spatial complexity O (1) opens up a fixed array size. Stability: stable.
Characteristics of insertion sorting:
The closer the initial data is to order, the higher the time efficiency.
3. Hill sort
3.1 principle
Hill ranking method is also known as reduced incremental method. The basic idea of hill sorting method is: first select an integer, divide all records in the sequence to be sorted into the integer group we selected, group from the first element, divide the two data into the same group according to the number of elements in each group, and directly insert and sort the records in each group. Then repeat the above grouping and sorting. Finally, all elements are divided into a group, and the last group can be sorted finally. Hill sort is the optimization of direct insertion sort. After repeated grouping, it is sorted to make the local order first, and then the overall order.
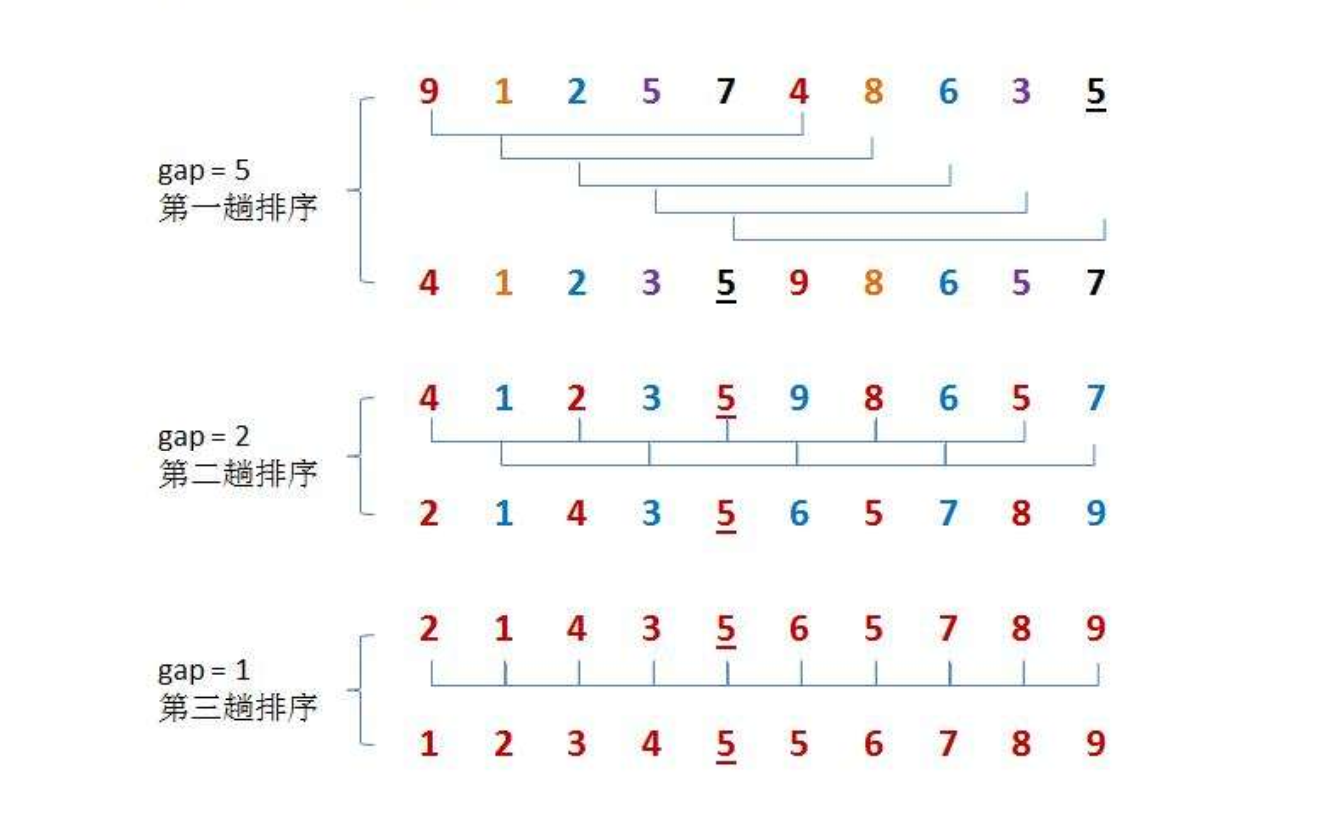
When gap > 1, the array is pre sorted in order to make the array closer to order. When gap == 1, the array is close to ordered, which will be very fast. In this way, the optimization effect can be achieved as a whole.
3.2 performance analysis:
According to the data structure by teacher Yan Weimin, the time complexity of hill sorting is related to the "increment". Time complexity is a function of "increment", but how to determine a perfect increment sequence has not been solved. According to the experiment and some data, the time complexity of hill sorting is O(n1.3)-O(n1.5), and the spatial complexity is O (n) For the incremental method, the book describes taking a number without a common factor other than one as an increment, that is, a prime number.
3.3 code implementation
public static void shell(int[] array,int gap) {
//Parameter judgment
if(array == null) return;
for (int i = gap; i < array.length; i++) {
int tmp = array[i];
int j = i-gap;
for (; j >= 0 ; j-=gap) {
if(array[j] > tmp) {
array[j+gap] = array[j];
}else {
break;
}
}
array[j+gap] = tmp;
}
}
public static void shellSort(int[] array) {
int gap = array.length;//The initial increment is the array length
while (gap > 1) {
shell(array,gap);
gap = gap/2;//1
}
shell(array,1);
}
Because the number of data we give is uncertain, we can't find a general formula to calculate our increment and make it a prime number. Therefore, as long as we follow a reasonable method to group the array, the increment will be gradually reduced each time, and finally divided into one group. The code above is basically the same as that of direct insertion sorting, except that i=gap here, and the content under is changed accordingly.
4. Select Sorting
4.1 direct selection sorting - principle
Select sorting. Select Sorting directly. In terms of ascending order, it is assumed that the first element is the smallest and is compared with the following elements in turn. It is assumed that the first element is larger than the compared element. Exchange their positions and do not do any operation. Compare the next element. When the array elements are compared, the first comparison ends and the first element is the minimum value, The second comparison assumes that the second element is the smallest. Compare and exchange with the following elements in turn. Repeat the first step. After comparing n-1 times, the elements are ordered.
4.2 realization
public static void selectSort(int[] array) {
if(array==null||array.length<2){
return;
}
for (int i = 0; i <array.length-1 ; i++) {
int min=i;//The default first element is the smallest
for (int j = i+1; j <array.length; j++){
if(array[min]>array[j]){
min=j;
}
}
if(min!=i){
int tem=array[i];
array[i]=array[min];
array[min]=tem;
}
}
}
4.3 performance analysis:
Time complexity * *: O(n^2) * * regardless of order or disorder, it can be properly optimized, that is, when comparing, such as ascending order, when the front elements are larger than the rear ones, do not exchange each time, use a temporary variable to record the minimum value, and then exchange after one pass of traversal, but the time complexity is still O(n^2), space complexity: o(1), stability: unstable row.
5. Heap sorting
5.1 principle

The basic principle is also selective sorting. Instead of finding the maximum number of unordered intervals by traversal, the maximum number of unordered intervals is selected by heap. * * heap is a complete binary tree logically
If the value of any node is greater than or equal to the value of the node in its subtree, it is called a large heap, or a large root heap, or a maximum heap. On the contrary, it is a small heap, or a small root heap, or a minimum heap. The value of the node in the subtree does not matter** In terms of ascending order, we create a large heap. Each time the element at the top of the heap is the largest, we exchange it with the last element of the heap. The element at the end of the heap is the maximum value, and the last element of the array is the maximum value. The ordered elements are excluded from the sorting range during the next exchange adjustment, and then adjust the exchange heap to continue to be a large root heap, Then repeat the above operation to get the second largest element for the second time until it is sorted to the top of the heap.
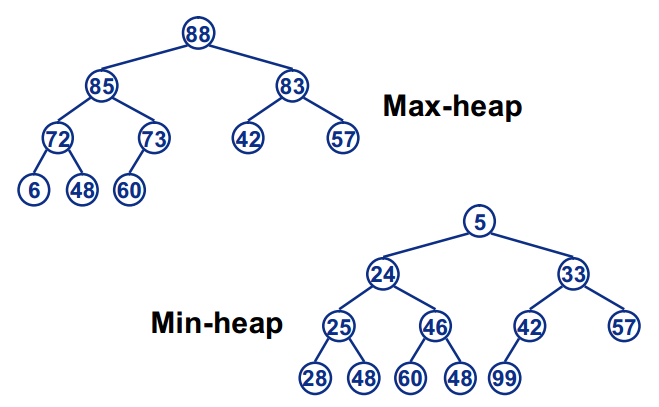
Note: a lot should be built in ascending order; In descending order, small piles should be built.
Then briefly summarize the basic idea of heap sorting:
a. The unordered sequence is constructed into a heap, and the large root heap or small root heap is selected according to the ascending and descending requirements;
b. Exchange the top element with the end element, and "sink" the largest element or the smallest element to the end of the array;
c. Readjust the structure to meet the heap definition, then continue to exchange the top element of the heap with the current end element, and repeat the adjustment + exchange steps until the whole array is in order.
5.2 realization
public static void shiftDown(int[] array,int parent,int len) {
int child = 2*parent+1;
while (child < len) {
if(child+1 < len && array[child] < array[child+1]) {
child++;
}
//The child subscript indicates the subscript of the maximum value of the left and right children
if(array[child] > array[parent]) {
int tmp = array[child];
array[child] = array[parent];
array[parent] = tmp;
parent = child;//If the subtree is not empty, just operate the subtree and change the subtree
child = 2*parent+1;
}else {
break;
}
}
}
public static void createBigHeap(int[] array) {
for (int i = (array.length-1-1)/2; i >= 0 ; i--) {
shiftDown(array,i,array.length);
}
}
/**
* Time complexity: O(N*logn)
* Space complexity: O(1)
* Stability: unstable
* @param array
*/
public static void heapSort(int[] array) {
createBigHeap(array);
int end = array.length-1;
while (end > 0) {
int tmp = array[0];
array[0] = array[end];
array[end] = tmp;
shiftDown(array,0,end);
end--;
}
}
5.3 performance analysis
Time complexity: * * O(n * log(n)), * * can be regarded as a complete binary tree, and each node needs to be exchanged. After the exchange, it needs to be down regulated. Whole space complexity: O(1)
6 bubble sorting
6.1 principle
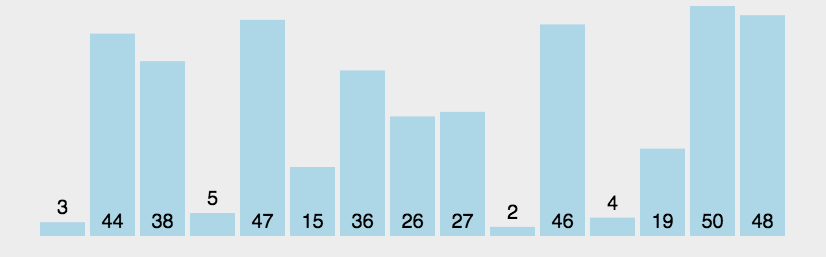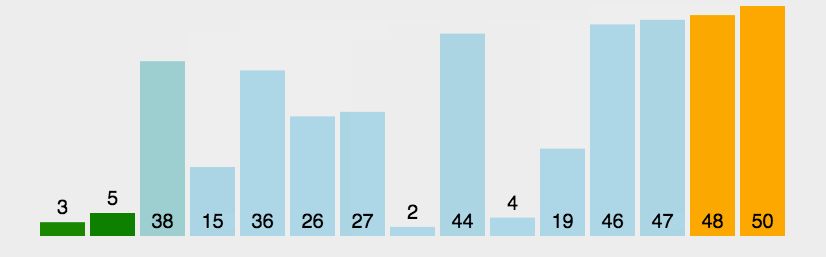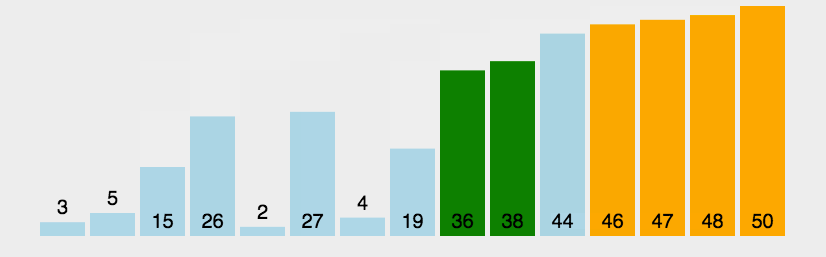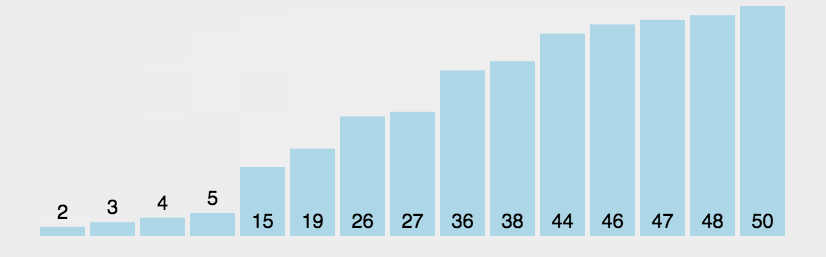
In the sequence to be sorted, through the comparison of adjacent numbers, gradually move the larger data to the back of the sequence to be sorted, and continue this process until the array is in order as a whole. Suppose n data only need to be compared n-1 times, and the maximum value in the disordered sequence is bubbled every time. For the first time, the number of comparisons is still n-1, and then the number of comparisons per time is reduced by 1. Until the N-1 comparison is completed, the data is in order. The following code has been optimized. When the sequence to be sorted itself is in order, the sorting is completed once.
public static void bubbleSort(int[] array) {
for (int i = 0; i < array.length-1; i++) {
boolean flg = false;//Make a mark to prevent the data itself from being orderly
for (int j = 0; j < array.length-1-i; j++) {//The comparison times of each trip are decreasing, so i should be reduced
if(array[j] > array[j+1]) {
int tmp = array[j];
array[j] = array[j+1];
array[j+1] = tmp;
flg = true;
}
}
if(flg == false) {
break;
}
}
}
6.2 performance analysis
Time complexity: in the case of O(N^2) data disorder, in the case of O(N) data order, space complexity O (1), stability: stable sorting.
7 quick sort (important)
7.1 principle - Overview
- Select a number from the interval to be sorted as the benchmark value (pivot);
- Partition: as a partition function, traverse the entire range to be sorted, place the smaller (can contain equal) than the benchmark value to the left of the benchmark value, and place the larger (can contain equal) than the benchmark value to the right of the benchmark value;
- Using the divide and conquer idea, the left and right cells are processed in the same way until the length between cells = = 1, which means that they are in order, or the length between cells = = 0, which means that there is no data.
7.1.1 pit excavation method:
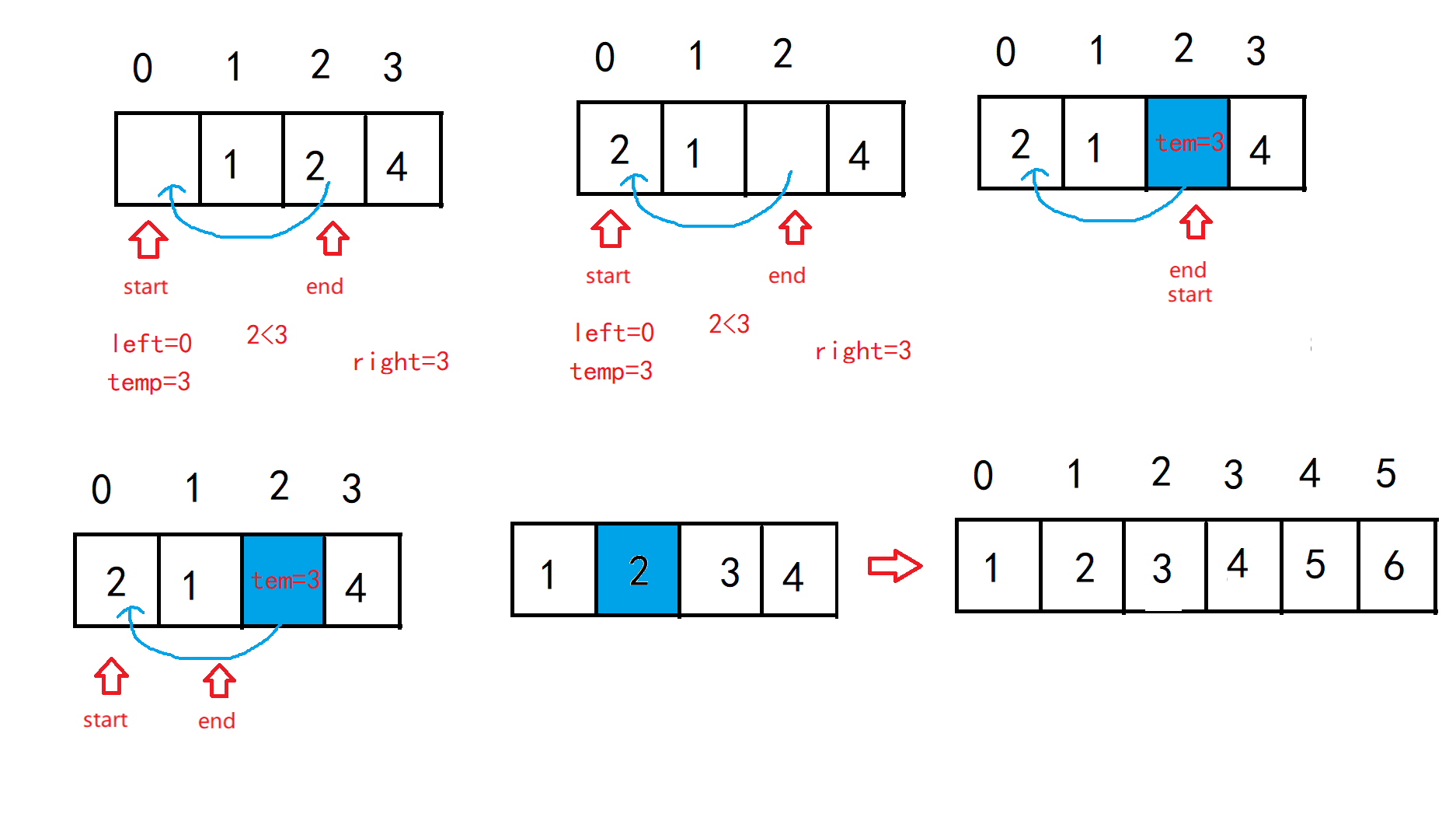
public static int partition(int[] array,int start,int end) {
int tmp = array[start];
while (start < end) {
//1. Judge first and then
while (start < end && array[end] >= tmp) {//A value less than the base point was found
end--;
}
//1.1 start array [start] = array [End]
array[start] = array[end];
//2. Then judge the front
while (start < end && array[start] <= tmp) {
start++;
}
//2.1 give the large one to end array [End] = array [start]
array[end] = array[start];
}
//start=end
array[start] = tmp;
return start;
}
//Similar to the preorder traversal of binary tree search tree, the benchmark is the root node of binary tree
public static void quickSort(int[] array,int left,int right) {
if(left >= right) {//Conditions for the end of recursion
return;
}
int pivot = partition(array,left,right);
quickSort(array,left,pivot-1);
quickSort(array,pivot+1,right);
}
public static void main(String[] args) {
int []arr={6,0,1,2,7};
System.out.println(Arrays.toString(arr));
quickSort(arr,0,arr.length-1);
System.out.println(Arrays.toString(arr));
}
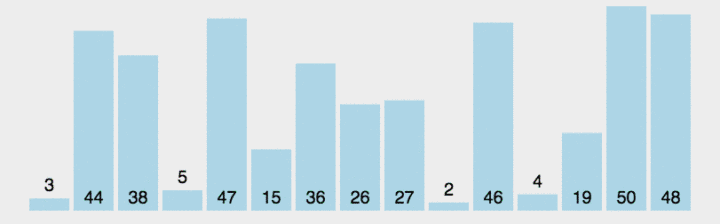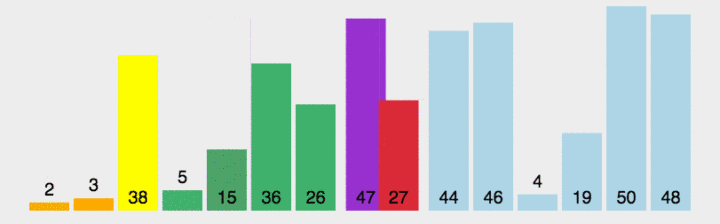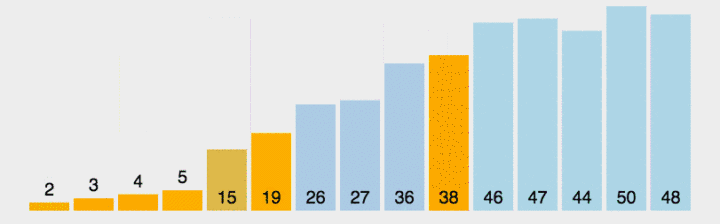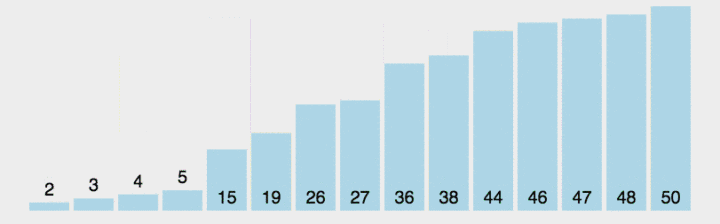
Suppose I take arrays 5, 1, 2, 4, 3 and 6 as an example to sort in ascending order. The general process is as follows. Let's see. For the first time, based on 5, it is divided as follows:
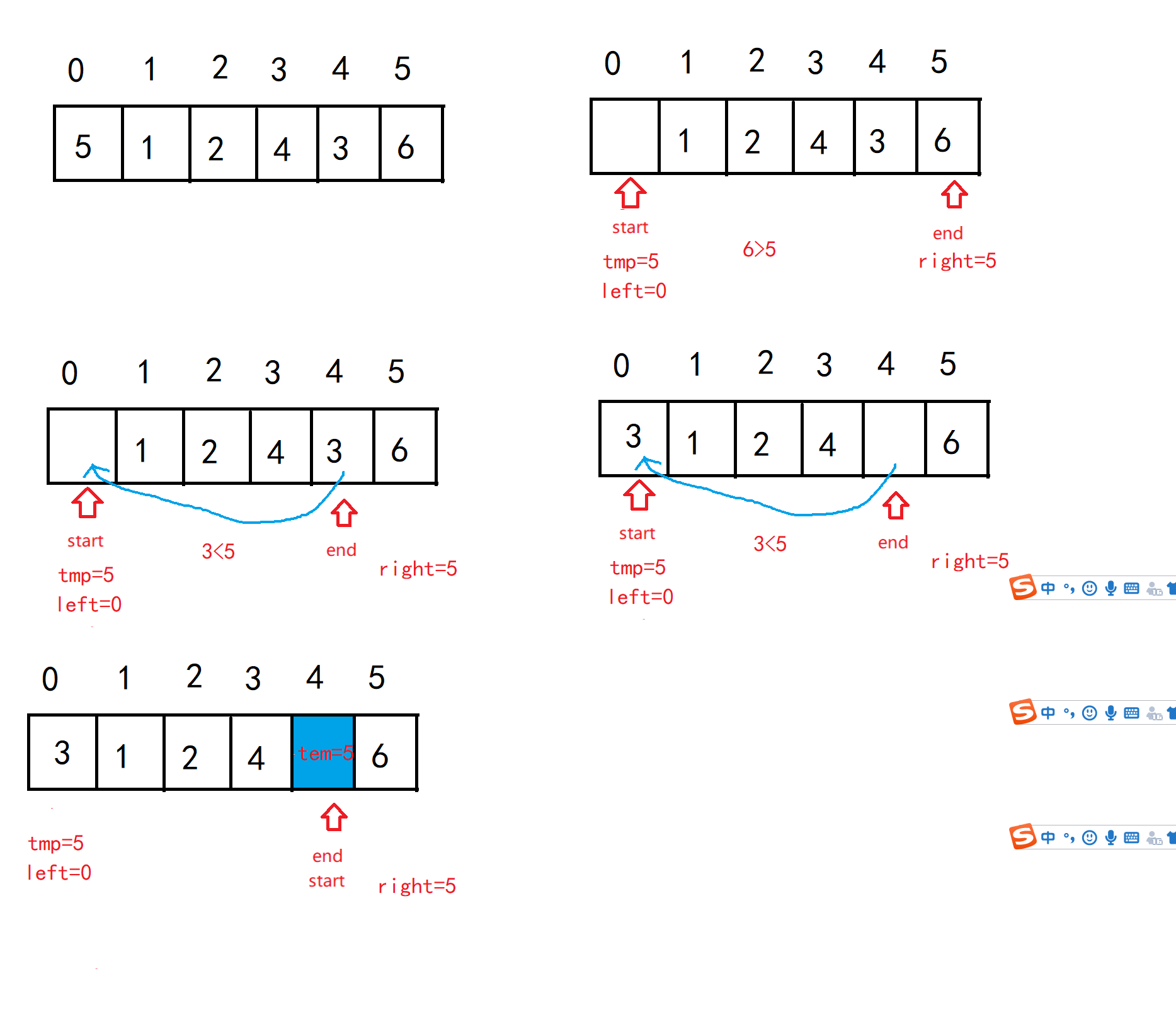
Then, in the same way, first divide the left and then the right, and keep recursing. There is no need to divide the sequence of numbers. It is orderly by default. After the division based on 3, 2 and 1, whether the left side of the first benchmark is in order, and then start sorting on the right, and then the whole sequence will be in order.
7.1.2:Hoare method:
The basic idea is the same as that of the pit digging method, except that the assignment is no longer carried out, but the exchange of two numbers is carried out, and an exchange function is realized:
public static void quickSort1(int[] array,int left,int right) {
if(left >= right) {//Conditions for the end of recursion
return;
}
int pivot = partition1(array,left,right);
quickSort(array,left,pivot-1);
quickSort(array,pivot+1,right);
}
public static int partition1(int[] array, int left, int right) {
int i = left;
int j = right;
int pivot = array[left];
while (i < j) {
while (i < j && array[j] >= pivot) {
j--;
}
while (i < j && array[i] <= pivot) {
i++;
}
swap(array, i, j);
}
swap(array, i, left);
return i;
}
// //Method of exchange
public static void swap(int[]array,int i,int j){
int tem=array[i];
array[i]=array[j];
array[j]=tem;
}
7.2 performance analysis
Time complexity: quick sort can be regarded as the preorder traversal of the binary tree. Each node is traversed as the benchmark, and the whole array is in order. In the best case, O(n * log(n)), each recursion evenly divides the sequence to be sorted, and the depth of the tree is multiplied by the traversal interval of each layer. In the worst case, O(n^2), when the data is ordered, it is a single branch tree. In the worst case of spatial complexity, O(n). Stability: unstable.
7.3 optimization of quick sort
For the divide and conquer algorithm, if the algorithm can be divided into two equal length subsequences each time, the efficiency of the divide and conquer algorithm will reach the maximum. In other words, the choice of benchmark is very important. The way of selecting the benchmark determines the length of the two sub sequences after two segmentation, which has a decisive impact on the efficiency of the whole algorithm. The most ideal method is that the selected benchmark can just divide the sequence to be sorted into two equal length subsequences.
7.3.1 fixed position method:
Basic quick sort selects the first or last element as the benchmark. But it is not a good method, * * because when the data is in order, the efficiency of this algorithm is very low, and only one number can be excluded after sorting each time, which has a great time complexity, * * just like the quick sort written above is the quick sort of fixed position method, so the following two more efficient benchmark selection methods are introduced.
7.3.2 randomly selected benchmark method (understanding)
Idea: using random numbers, take any element in the sequence to be arranged as the benchmark
public static void quickSort(int[] array,int left,int right) {
if(left >= right) {//Conditions for the end of recursion
return;
}
// 1. Randomly select the benchmark - "first change the value of the left subscript
//rand swap array [left] array [rand]
Random random = new Random();
int rand = random.nextInt(right-left)+left+1;
swap(array,left,rand);
int pivot = partition(array,left,right);
quickSort(array,left,pivot-1);
quickSort(array,pivot+1,right);
}
The randomly selected benchmark method is more efficient than the fixed position method, but there is great chance. It does not rule out that the benchmark you select each time is the maximum or minimum value in the sequence to be sorted, nor can you divide the sequence to be sorted evenly.
7.3.3 medium of three (optimized and orderly data)
In fact, the best way is to find the middle value of the array to be sorted and divide it. When this is difficult to get, the general way is to use the median of the three elements at the left, right and center as the benchmark value. Obviously, the three number median segmentation method eliminates the bad situation of pre sorting input.
public static void medianOfThree(int[] array,int left,int right) {
int mid = (left+right)/2;
if(array[mid] > array[left]) {
int tmp = array[mid];
array[mid] = array[left];
array[left] = tmp;
}//array[mid] <= array[start]
if(array[left] > array[right]) {
int tmp = array[left];
array[left] = array[right];
array[right] = tmp;
}//array[start] <= array[right]
if(array[mid] > array[right]) {
int tmp = array[mid];
array[mid] = array[right];
array[right] = tmp;
}
//array[mid] <= array[start] <= array[right]
}
//Similar to the preorder traversal of binary tree search tree, the benchmark is the root node of binary tree
public static void quickSort(int[] array,int left,int right) {
if(left >= right) {//Conditions for the end of recursion
return;
}
//2. Triple median method
medianOfThree(array,left,right);
int pivot = partition(array,left,right);
quickSort(array,left,pivot-1);
quickSort(array,pivot+1,right);
}
7.3.4 using insert sort
We know that the characteristic of insertion sort is that the more ordered the data, the faster the sorting speed. When the length of the sequence to be sorted is divided to a certain size, the length of the sequence to be sorted is between 5 ~ 20. Any cut-off range can use direct insertion sort instead of quick sort.
public static void insertSort2(int[] array,int left,int right) {
//Parameter judgment
if(array == null) return;
for (int i = left+1; i <= right; i++) {
int tmp = array[i];
int j = i-1;
for (; j >= left ; j--) {
if(array[j] > tmp) {
array[j+1] = array[j];
}else {
break;
}
}
array[j+1] = tmp;
}
}
//3. After recursive execution to an interval, the direct insertion sort is added to the lead quick sort
if((right - left + 1) <= 20) {
insertSort2(array,left,right);
return;//
}
7.3.5 non recursive quick sort
The Quicksort we usually see is a recursive version, and does not focus on non recursive methods. But the non recursive version is also well implemented, because the essence of recursion is stack. In the process of non recursive implementation, non recursive can be realized by saving intermediate variables with the help of stack. The following non recursion also looks at (*  ̄)  ̄).
public static void quickSort2(int[] array) {
Stack<Integer> stack = new Stack<>();
int start = 0;
int end = array.length-1;
int pivot = partition(array,start,end);
if(pivot > start+1) {
stack.push(start);
stack.push(pivot-1);
}
if(pivot < end-1) {
stack.push(pivot+1);
stack.push(end);
}
while (!stack.empty()) {
end = stack.pop();
start = stack.pop();
pivot = partition(array,start,end);
if(pivot > start+1) {
stack.push(start);
stack.push(pivot-1);
}
if(pivot < end-1) {
stack.push(pivot+1);
stack.push(end);
}
}
}
8. Merge and sort (important)
8.1 principle
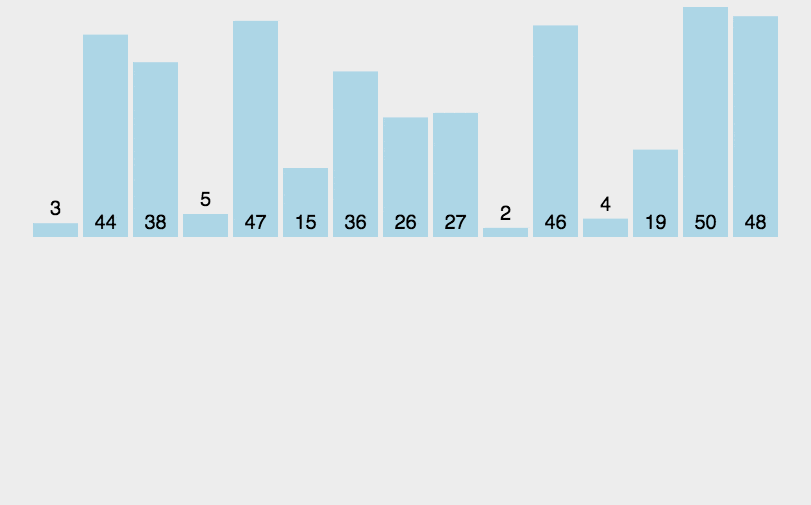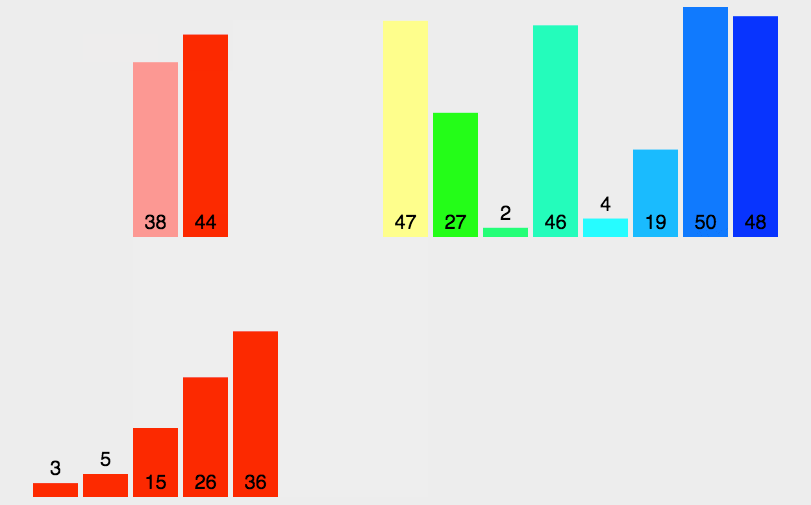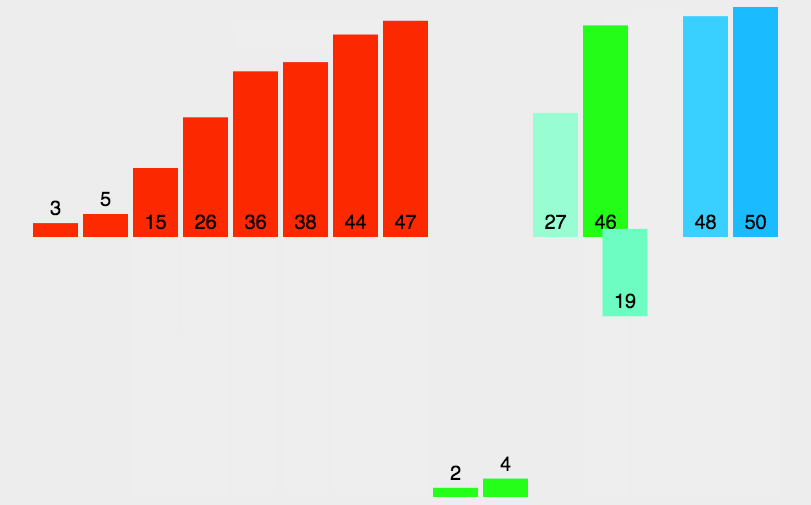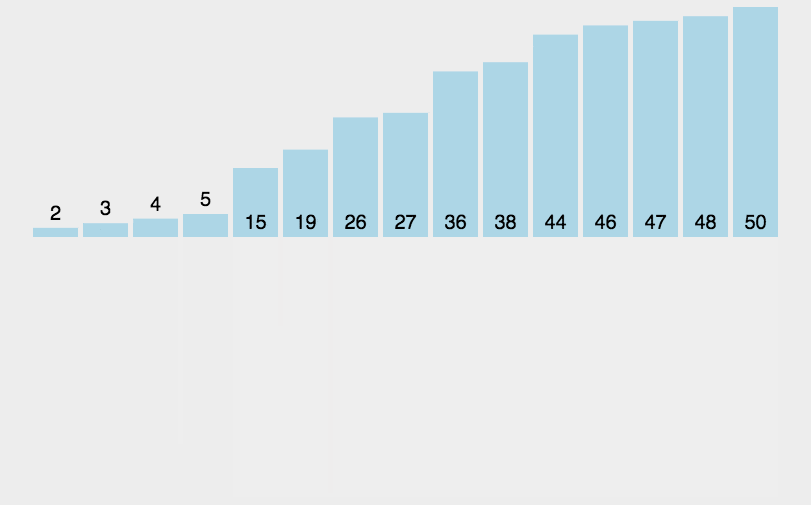
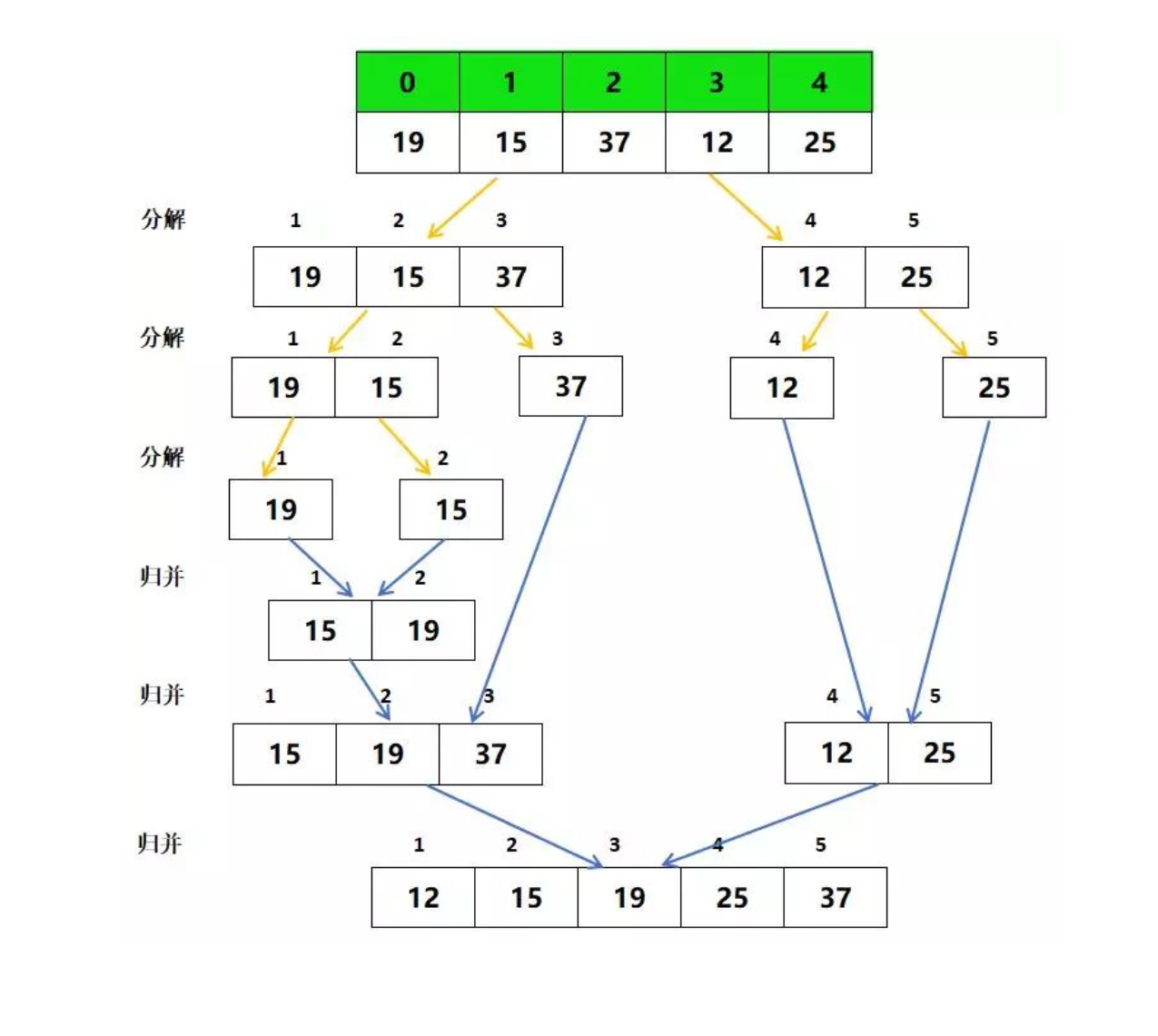
Merge sort is an effective sort algorithm based on merge operation. It is a very typical application of divide and conquer== The core is to decompose and then merge into an ordered sequence. First divide the sequence to be sorted into left and right parts to make the two parts orderly respectively, and then merge, so that the whole is orderly. For the sequences on the left and right, the same operation is a merging and sorting, which is a subproblem with the same structure== The decomposition process can be analogous to the preorder traversal of a binary tree. Each sequence is a binary tree, with roots first, then left and then right. First decompose it into one number, one number is orderly, and then merge it into two numbers, which is orderly. Then, the sequence of two combined four numbers is orderly, and so on. The whole sequence is orderly.
public static void merge(int[] array,int left,int right,int mid) {
//The following is the operation of merging two ordered arrays
int[] tmp = new int[right-left+1];//The temporary array is used to store the sorted sequence
int k = 0;
int s1 = left;
int e1 = mid;
int s2 = mid+1;
int e2 = right;
while (s1 <= e1 && s2 <= e2) {
if(array[s1] <= array[s2]) {
tmp[k++] = array[s1++];
}else {
tmp[k++] = array[s2++];
}
}
while (s1 <= e1) {
tmp[k++] = array[s1++];
}
while (s2 <= e2) {
tmp[k++] = array[s2++];
}
for (int i = 0; i < k; i++) {
//Put the ordered numbers in the appropriate position of the original array
array[i+left] = tmp[i];
}
}
public static void mergeSort1(int[] array,int left,int right) {
if(left >= right) {//The condition for the end of recursion is to divide the sequence to be sorted into a number and terminate the recursion
return;
}
int mid = (left+right)/2;
mergeSort1(array,left,mid);//Recursive left sequence
mergeSort1(array,mid+1,right);//Recursive right sequence
merge(array,left,right,mid);//Merge ordered sequence
}
8.2 performance analysis
Time complexity: O(n * log(n)), the number of layers of binary tree multiplied by the data of each layer, spatial complexity: O(n), stability: stable.
8.3 non recursive version
Non recursive merging and sorting starts from small to large. Contrary to the recursive idea, the core idea is to merge two ordered arrays, compare two segments and two segments into one ordered segment, and then merge the previous ordered segments. First, there is a number in one segment during comparison, and then the number of segments increases twice, After that, the number of segments divided is greater than or equal to the length of the array. At this time, the sequence to be sorted is ordered.
Non recursive time complexity::, O(n * log(n)), space complexity: O(n)
//Non recursive version
public static void merge2(int[] array,int gap) {
int[] tmp = new int[array.length];
int k = 0;
int s1 = 0;
int e1 = s1+gap-1;//0+1-1
int s2 = e1+1;
int e2 = s2+gap-1 >= array.length ? array.length-1 : s2+gap-1;//e2 exceeded
//There must be two segments s2 to judge that e2 cannot be used. s2 has at least one data in the second segment
while (s2 < array.length) {//
while (s1 <= e1 && s2 <= e2) {
if (array[s1] <= array[s2]) {
tmp[k++] = array[s1++];
}else {
tmp[k++] = array[s2++];
}
}
while ( s1 <= e1 ) {
tmp[k++] = array[s1++];
}
while (s2 <= e2) {
tmp[k++] = array[s2++];
}
s1 = e2+1;
e1 = s1+gap-1;
s2 = e1+1;
e2 = s2+gap-1 >= array.length ? array.length-1 : s2+gap-1;
}
//There is only the first paragraph left
while (s1 <= array.length-1) {//S1 and E1 may also exceed the range of the array
tmp[k++] = array[s1++];
}
//I don't care if there's not a paragraph left
for (int i = 0; i < k; i++) {
array[i] = tmp[i];
}
}
public static void mergeSort(int[] array) {
for (int gap = 1; gap < array.length; gap*=2) {//Recursion is decomposition, and non recursion is merging. First, a number is a group of order, then two are a group of order, and so on
merge2(array,gap);
}
}
The non recursive version has a lot of details, which is difficult to write compared with recursion. Next, I list the general details of recursion in a graphical way. When writing the code, we just need to pay attention to some boundary conditions: the S1, E1, S2 and E2 variables in the code are the start position and end position of the first paragraph of the two sorting sequence, Start and end positions of the second segment (all positions cannot exceed the array subscript)
In the case of only one segment:


8.4 sorting of massive data
The traditional sorting algorithm generally refers to the internal sorting algorithm, which aims at the situation that all data can be loaded into memory at one time. However, in the face of massive data, the unit may be GB,TB or above, while the memory is only dozens of G, that is, the data cannot be loaded into the memory at one time. These data are stored in the external memory, and the external sorting method needs to be used. Because the computer accesses the memory much faster than the external memory, but the memory is more expensive, the external sorting adopts the block method (divide and rule), first divide the data into blocks, and select an efficient internal sorting strategy for the data in the block. Then the idea of merging sorting is used to sort all blocks to get an ordered sequence of all data.
For example, consider a 100G file with 1G of available memory. First, the files are divided into 200 copies, each 512M, and then loaded into the memory for sorting. Finally, the results are stored in the hard disk. The result is 200 files sorted separately. Then perform 200 channel merging, load certain data from each file into the input cache, merge and sort the data in the input cache, write the data on the hard disk after the output cache is full of data, and then empty the cache to continue writing the next data. For the input buffer, when the data in the divided small file is sorted, the next data of the file is loaded until all 200 copies of all data have been loaded into memory and processed. Finally, we get a 100G sorted file on the hard disk.
9 other non comparison based sorting (understand)
9.1 counting and sorting
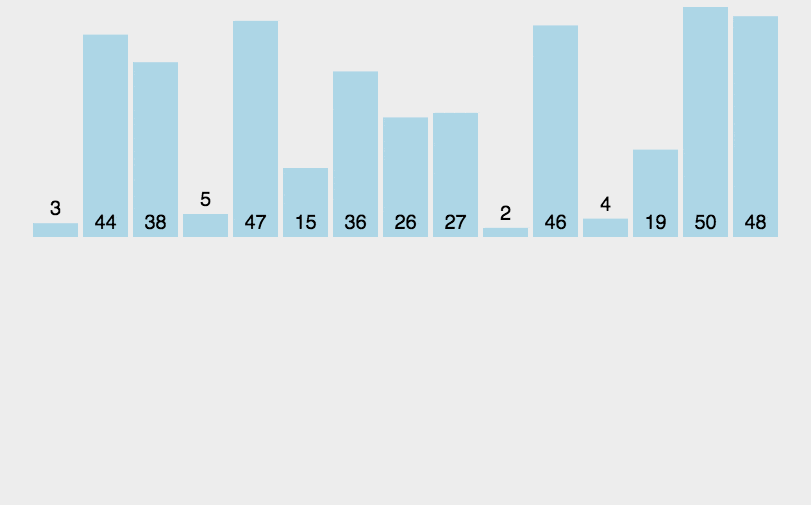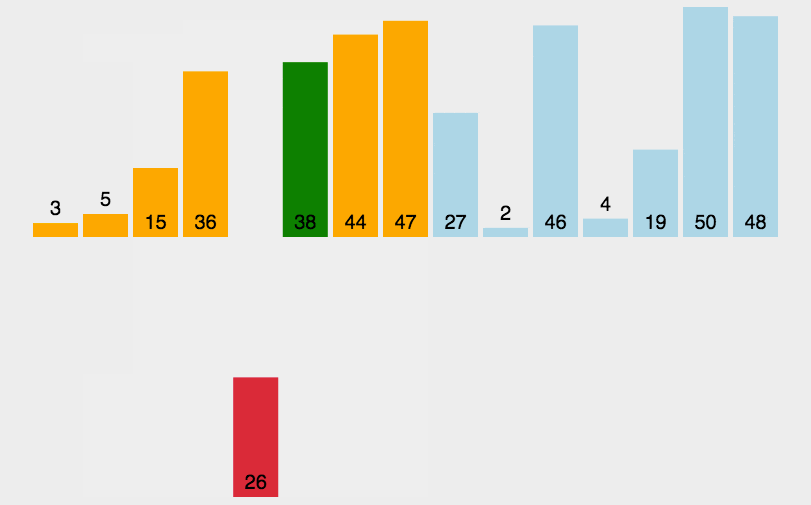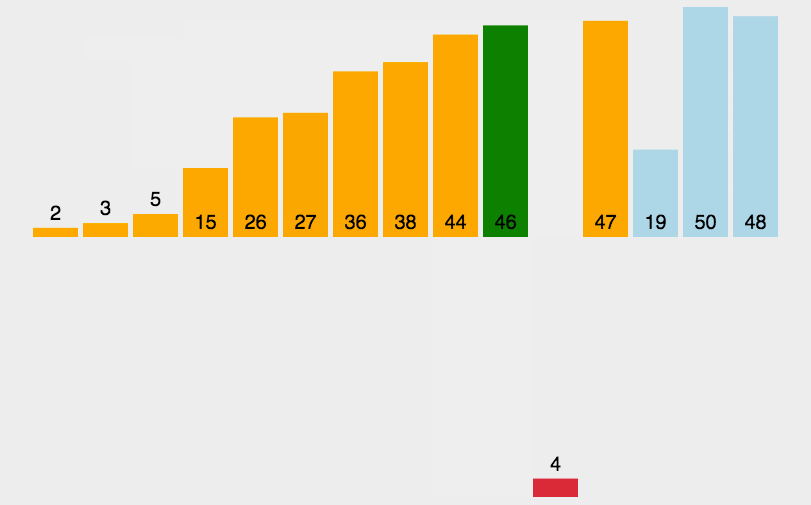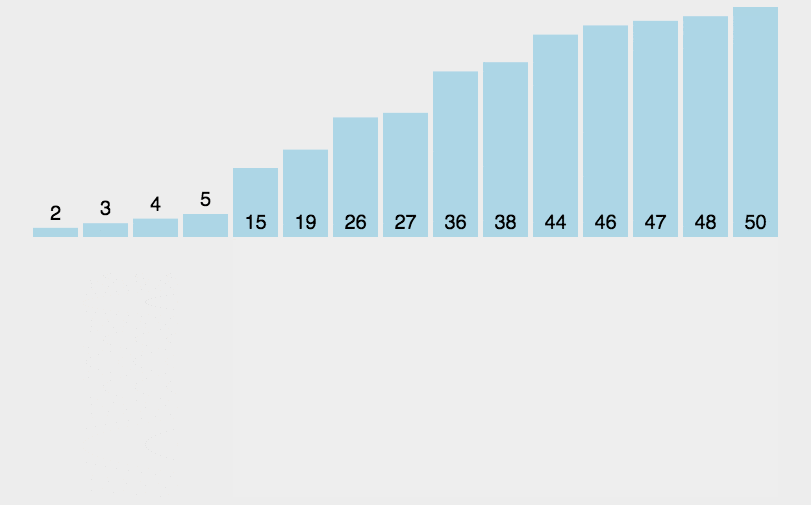
**Basic idea: for each element to be sorted, if you know how many smaller elements are in the array to be sorted, you can directly get where the element should be after sorting** The reason why it is called non comparison based sorting is that there is no direct comparison and exchange for data sorting, but through some other ideas. The specific ideas are shown in the figure:
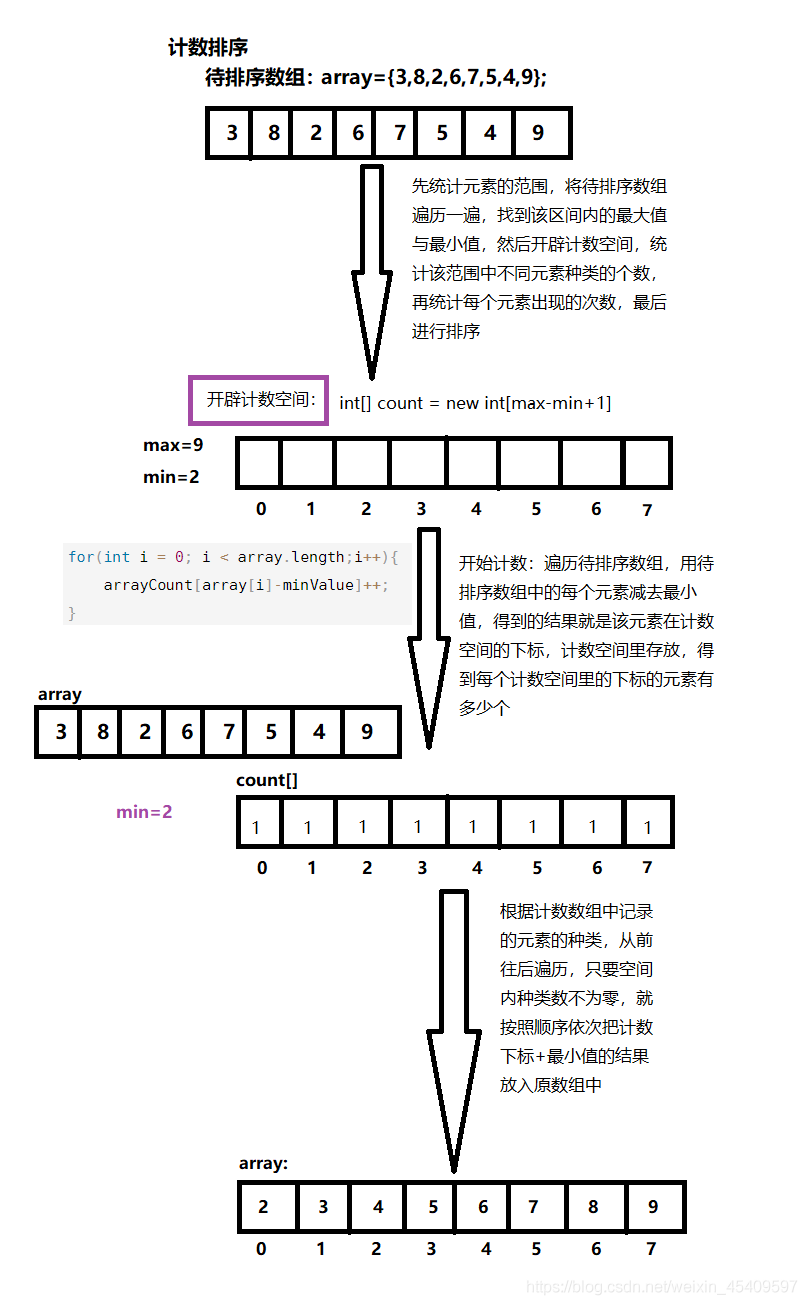
Code example:
public class TestDemo {
public static int [] countSort(int[] array){
//1. To count the range of elements, first find the maximum and minimum values in the array
int minValue = array[0];
int maxValue = array[0];
for(int i = 1 ;i<array.length;i++){
if(array[i]>maxValue){
maxValue = array[i];
}
if(array[i]<minValue){
minValue = array[i];
}
}
//2. Open up counting space: the maximum number of different element types contained in this range
int range = maxValue-minValue+1;
//System.out.println(range);
int[] arrayCount = new int[range];
//3. Count the number of occurrences of each element
for(int i = 0; i < array.length;i++){
try {
arrayCount[array[i]-minValue]++;//Storage location of array[i]-minValue element
}catch (Exception e ){
e.printStackTrace();
}
}
int begin=0;
//Create a new array to store the sorted results
int []num=new int[array.length];
//4. Sort elements
for (int i = 0; i < arrayCount.length; i++) {
if(arrayCount[i]!=0){
for (int j = 0; j <arrayCount[i] ; j++) {
num[begin++]=minValue+i;//Take the elements as you put them
}
}
}
return num;
}
public static void main(String[] args) {
int [] array={7,4,9,3};
System.out.println(Arrays.toString(array));
int [] num=countSort(array);
System.out.println(Arrays.toString(num));
}
}
Of course, non comparison based sorting, cardinality sorting and bucket sorting are also non comparison based sorting, which is also simple. I won't introduce them here.
Pass by friends remember to praise and support, thank you!!!
