Station B learning portal – > Shang Silicon Valley Java data structure and Java algorithm (Java data structure and algorithm)

Scenario introduction

Assuming that there are 7 villages ready to build roads, how can we choose to minimize the mileage of road construction and connect all villages?

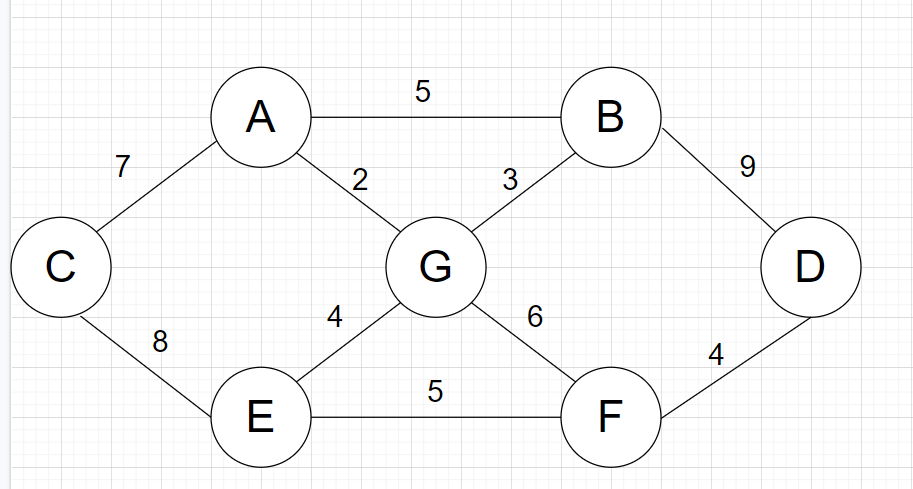
If it is directly connected, the weight may be relatively large;
In fact, this problem can be transformed into the problem of constructing the minimum spanning tree;

minimum spanning tree :
The spanning tree of a connected graph with n nodes is the minimal connected subgraph of the original graph, contains all N nodes in the original graph, and has the least edges to keep the graph connected. The minimum spanning tree can be obtained by kruskal algorithm or prim algorithm.

Kruskal algorithm will be studied later in this article. In this study, PLIM algorithm is used to solve this problem;

Prim algorithm (PRIM algorithm), an algorithm in graph theory, can search the minimum spanning tree in the weighted connected graph. That is, the tree composed of edge subsets searched by this algorithm not only includes all vertices (English: Vertex (graph theory)) in the connected graph, but also the sum of the weights of all edges is the smallest.

Step analysis

When solving the minimum spanning tree by prim algorithm, n-1 edges need to be generated for n nodes; And is a minimal connected subgraph;

Specific process:
Define connected graph G:(V,E), minimum spanning tree: T:(U,D),
Starting from the first vertex of connected graph G, find the path with the smallest weight, put it into the minimum spanning tree, and mark the node connected by this path as visited,
Then the two vertices start separately, find the shortest path,... And repeat the operation; Until all vertices in the connected graph are accessed;

Graphic process:
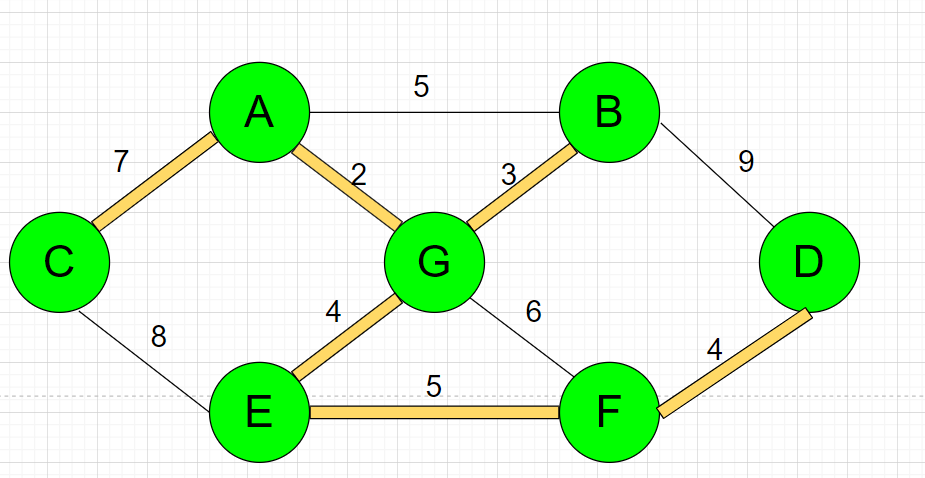
(1) For example, first find the first village A, compare the paths AB5, AC7 and ag2 and find that AG is the shortest, then connect village A with village g; At this time, A and G are marked as visited nodes
Then, the starting point is point A and point G
(2) After comparing paths AB5, AC7, GB2, ge4 and GF6, find the shortest path GB. Connect village G with village B; B. mark the village as visited node;
At this time, the starting point is point A, point B and point G;

(3) After comparing paths AC7, GE4, GF6 and bd9, find the shortest path GE, connect village G with village E, and mark village E as an visited node;
At this time, the starting points are point A, point B, point G and point E;
(4) After comparing paths AC7, GF6, bd9, EC8 and EF5, find the shortest path EF, connect village f with village E, and mark village F as an visited node;
At this time, the starting point is point A, point B, point G, point E and point F;
(5) After comparing paths AC7, bd9, EC8 and FD4, find the shortest path FD, connect village d with village F, and mark village D as an visited node;
At this time, the starting point is point A, point B, point G, point E, point F and point D;
(6) After comparing paths AC7 and EC8, find the shortest path AC, connect village C with A, and mark Village C as an visited node;
Completion of road construction; Get the shortest path 25

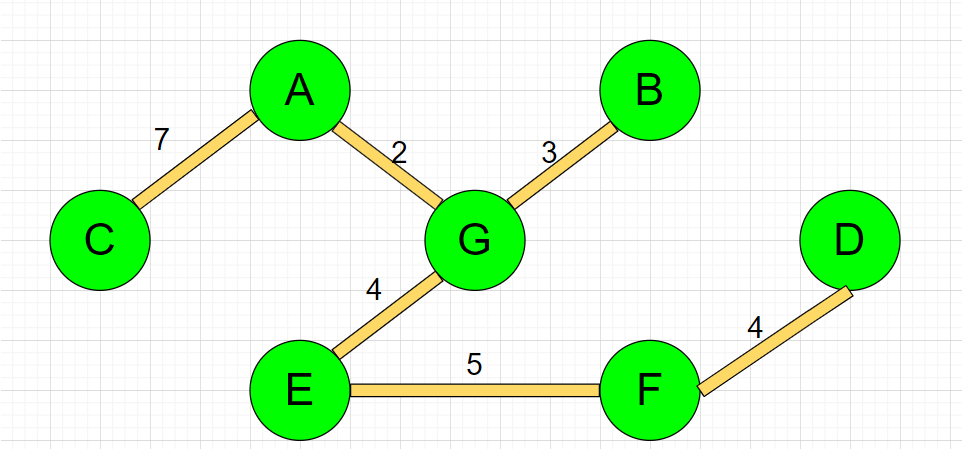
Concrete implementation

/**
 * @author by CSDN@Xiaozhi RE0
 * @date 2021-12-07
 * Prim Algorithm 
 */
public class PrimAlgorithm {
    public static void main(String[] args) {
        //Construct the map of village road construction;
        char[] village = {'A', 'B', 'C', 'D', 'E', 'F', 'G'};
        //Number of villages;
        int size = village.length;
        //Manually construct the connection weight adjacency matrix between villages;
        int[][] villagePrimitive
                = {{Integer.MAX_VALUE, 5, 7, Integer.MAX_VALUE, Integer.MAX_VALUE, Integer.MAX_VALUE, 2},
                {5, Integer.MAX_VALUE, Integer.MAX_VALUE, 9, Integer.MAX_VALUE, Integer.MAX_VALUE, 3},
                {7, Integer.MAX_VALUE, Integer.MAX_VALUE, Integer.MAX_VALUE, 8, Integer.MAX_VALUE, Integer.MAX_VALUE},
                {Integer.MAX_VALUE, 9, Integer.MAX_VALUE, Integer.MAX_VALUE, Integer.MAX_VALUE, 4, Integer.MAX_VALUE},
                {Integer.MAX_VALUE, Integer.MAX_VALUE, 8, Integer.MAX_VALUE, Integer.MAX_VALUE, 5, 4},
                {Integer.MAX_VALUE, Integer.MAX_VALUE, Integer.MAX_VALUE, 4, 5, Integer.MAX_VALUE, 6},
                {2, 3, Integer.MAX_VALUE, Integer.MAX_VALUE, 4, 6, Integer.MAX_VALUE}};
        //View the initialized data;
        Graph graph = new Graph(size);
        MST mst = new MST();
        mst.getMST(size, graph, village, villagePrimitive);
        mst.printGraph(graph);
        //Calculate the shortest path;
        mst.primAlgorithm(graph, 0);
    }
}

//Foundation drawing;
class Graph {
    //Apex;
    public char[] node;
    //Path weight;
    public int[][] weight;
    //Number of vertices;
    public int size;

    //initialization; size: number of nodes;
    public Graph(int size) {
        this.node = new char[size];
        this.weight = new int[size][size];
        this.size = size;
    }
}

//Minimum spanning tree;
class MST {
    /**
     * Generate minimum tree
     * @param size   Number of nodes in graph
     * @param graph  Constructed graph
     * @param node   vertex
     * @param weight Weight 
     */
    public void getMST(int size, Graph graph, char[] node, int[][] weight) {
        for (int i = 0; i < size; i++) {
            graph.node[i] = node[i];
            System.arraycopy(weight[i], 0, graph.weight[i], 0, size);
        }
    }

    /**
     * Simple pulim algorithm; Find the minimum weight edge path at the current node as the starting point, and print the path;
     * @param graph Diagram of current problems
     * @param index Current node index
     */
    public void primAlgorithm(Graph graph, int index) {
        //Define an access array;
        boolean[] isVisited = new boolean[graph.size];
        //The current point marks him as visited first;
        isVisited[index] = true;
        //Two nodes to be connected start,end
        int start = -1;
        int end = -1;
        //The shortest path;
        int minPath = Integer.MAX_VALUE;
        //Final path and;
        int total = 0;
        //Will eventually walk 6 times;
        for (int i = 1; i < graph.size; i++) {
            for (int j = 0; j < graph.size; j++) {
                for (int k = 0; k < graph.size; k++) {
                    //What you are looking for is not accessible;
                    if (isVisited[j] && !isVisited[k] && minPath > graph.weight[j][k]) {
                        minPath = graph.weight[j][k];
                        start = j;
                        end = k;
                    }
                }
            }
            System.out.println("current path" + graph.node[start] + "-->" + graph.node[end] + "Weight is->" + minPath);
            //Final path and splicing;
            total += minPath;
            //Finally, set the qualified node as accessed;
            isVisited[end] = true;
            //Shortest path reset;
            minPath = Integer.MAX_VALUE;
        }

        System.out.println("Final plan,The shortest path is-->"+total);
    }


    /**
     * Adjacency matrix of printed graph
     *
     * @param graph chart
     */
    public void printGraph(Graph graph) {
        for (int[] weight : graph.weight) {
            System.out.println(Arrays.toString(weight));
        }
    }
}

test result

[2147483647, 5, 7, 2147483647, 2147483647, 2147483647, 2]
[5, 2147483647, 2147483647, 9, 2147483647, 2147483647, 3]
[7, 2147483647, 2147483647, 2147483647, 8, 2147483647, 2147483647]
[2147483647, 9, 2147483647, 2147483647, 2147483647, 4, 2147483647]
[2147483647, 2147483647, 8, 2147483647, 2147483647, 5, 4]
[2147483647, 2147483647, 2147483647, 4, 5, 2147483647, 6]
[2, 3, 2147483647, 2147483647, 4, 6, 2147483647]
current path A-->G Weight is->2
 current path G-->B Weight is->3
 current path G-->E Weight is->4
 current path E-->F Weight is->5
 current path F-->D Weight is->4
 current path A-->C Weight is->7
 Final plan,The shortest path is-->25