Random Forest (RF) is a simple and easy-to-use machine learning algorithm. Even without super parameter adjustment, the Random Forest can still obtain good results in most cases. It can be used for classification tasks and regression tasks. It is one of the commonly used machine learning algorithms.
1, Random forest principle
1. Basic thought
Random forest is a supervised learning algorithm. The "forest" constructed by it is a set of decision trees, which is usually integrated by Bagging algorithm. Random forest first uses the trained classifier set to classify the new samples, and then counts the results of all decision trees by majority voting or averaging the output. Because each decision tree in the forest is independent, it can obtain better performance than a single decision tree by voting and averaging.
2. Bagging algorithm
Because the random forest usually uses bagging algorithm to integrate the decision tree, it is necessary to understand the workflow and principle of bagging algorithm. The classification accuracy of some classifiers is sometimes only slightly better than random guess. Such classifiers are called weak classifiers. In order to improve the performance of classifiers, ensemble learning is usually used to combine several weak classifiers to generate a strong classifier. Bagging algorithm and Boosting algorithm are the basic algorithms in the field of integrated learning.
(1) Bagging algorithm flow
The process of Bagging algorithm is divided into two stages: training and testing.
(1) training stage
The Bootstrapping sampling method is used to randomly select N training samples from the original training set, and then put the N training samples back to the original training set for k rounds of extraction to obtain k training subsets. These k training subsets are used to train k basic models (the basic model can be decision tree or neural network, etc.).
(2) test phase
For each test sample, all trained basic models are used for prediction; After that, the results of all k basic models are combined for prediction. If it is a regression problem, the prediction average of K basic models is used as the final prediction result; If it is a classification problem, vote on the classification results of K basic models, and the category with the most votes is the final classification result.
(2) Bootstrapping sampling method
The implementation of bootstrapping method is very simple. It is assumed that the sample size is n: there are samples put back in the original sample, which are extracted n times. Each time, a new sample is formed. Repeat the operation to form many new samples. Through these samples, a distribution of samples can be calculated.
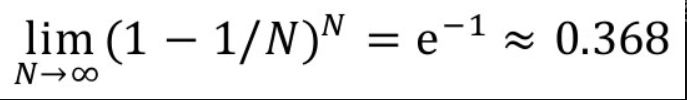
That is, when N is large enough, about 36.8% of the data in the training set will not be sampled in each round of random sampling of Bagging algorithm. This part of the data that has not been extracted is called Out Of Bag (OOB). Since these data are not involved in training, they can be used to verify the generalization ability of the model.
3. Principle of Bagging algorithm
Assuming that there are three classifiers, 17 samples are tested respectively. If errors are rare, each classifier may make errors on different samples. Suppose that the prediction results of the three classifiers are shown in the figure below, each sample is incorrectly classified at most once, and the labels of other categories are correct. If the final prediction of each sample is voted by the results of three classifiers, each sample will get the correct prediction. It's like that although one person occasionally makes a wrong judgment, it will be corrected by the correct judgment of others.
 Schematic diagram of prediction results of three classifiers
Schematic diagram of prediction results of three classifiers
An important conclusion can be drawn from the above examples, that is, if each classifier tends to make mistakes in different samples, the Bagging algorithm will achieve good results.
4. Random forest
From the previous analysis, Bagging algorithm can effectively prevent over fitting. Its principle is to improve the probability of obtaining correct conclusions during voting by encouraging the diversity of weak classifiers (that is, different weak classifiers make mistakes in different samples as much as possible).
Random forest uses decision tree as the basic model of Bagging algorithm, and increases the diversity between decision trees through "random" steps, so as to improve the prediction accuracy. Obviously, "random" is the key of random forest algorithm. It guarantees randomness through two parts, that is, to ensure the diversity among trees. Firstly, the Bootstrapping sampling method is used to ensure the independence of the training subset; Secondly, when the nodes of the tree are segmented, the sample feature (attribute) subset is randomly selected, and the best segmentation attribute is calculated from the feature subset. Specifically, if a sample contains n attributes, m (m < n) attributes are randomly selected from the N attributes to form a feature subset, and then the best segmentation attributes are selected within the range of the feature subset, so as to ensure the diversity of the decision tree.
2, OpenCV function description
The random forest in OpenCV is realized according to the random forest theory of Leo Breiman (random forest is a combined classification algorithm proposed by Leo Breiman in 2001). For the classification problem, the random forest chooses the category with the most votes as the output by voting on the prediction category of each tree; For the regression problem, the random forest calculates the average value of all trees as the total output. In order to improve robustness, random forests use out of bag data (OOB) to verify segmentation, usually setting the number of OOB to one-third of all data samples.
In random forest, all trees are trained with the same parameters, but the training sets are different. As mentioned earlier, on each node of each tree, not all attributes are used to find the best segmentation, but to find the best attribute in the random subset of attributes. For each node, a new subset of attributes is generated. For all nodes and all trees, the size of their attribute subsets is fixed. If the total number of attributes is n, the number of features in the attribute subset is set to round √  ̄ n by default during training. In addition, all decision trees are not pruned.
The cv::ml::RTrees class in the random forest inherits from the cv::ml::DTrees class of the decision tree.
Create an empty model using the cv::ml::RTrees::create function
Use the cv::ml::Algorithm::load function to load the pre trained model
Parameter description when building random forest model:
(1) set the size of feature (attribute) subset:

Set the size of randomly selected feature subsets on each tree node, which can be used to find the best segmentation. If it is set to 0, the size is set to the square root of the total number of features, and its default value is 0. This parameter is the only key parameter of random forest. You can use the cv::ml::RTrees::getActiveVarCount function to obtain the size of the current feature subset.
(1) set the size of feature (attribute) subset:
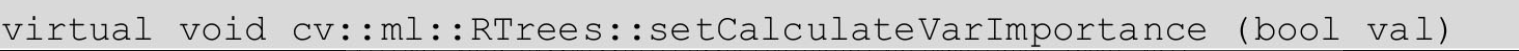
If val= true, the importance of the variable is calculated, and its default value is false. You can check whether to calculate the importance of a variable through the cv::ml::RTrees::getCalculateVarImportance function. If set to true, there will be additional time overhead. You can retrieve the importance of variables through the cv::ml::RTrees::getVarImportance function.
(3) importance of obtaining sample characteristics:

In the training phase, if setCalculateVarImportance is set to true, the variable importance array can be calculated. If it is set to false, the empty matrix will be returned.
(4) set algorithm termination conditions:

The termination condition can be set to train a specified number of trees and add them to the forest, or the termination condition can be set to achieve sufficient accuracy (measured by OOB error). Generally speaking, the more trees you have, the better the accuracy. However, the improvement of accuracy usually decreases after more than a certain number of trees. It should be noted that the prediction time increases linearly with the increase of the number of trees. The default value is TermCriteria(TermCriteria::MAX_ITERS+TermCriteria::EPS, 50, 0.1), indicating that the maximum number of trees is 50, or the OOB error is < 0.1. You can use the cv::ml::RTrees::getTermCriteria function to get the current termination condition.
The random forest also uses the cv::ml::StatModel::train function to train the model
The standard cv::ml::StatModel::predict function is used to predict the response of a single sample
Use the cv::ml::StatModel::calcError function to calculate the error on the training set or test set in the data set at one time (opencvsharp has not been implemented as of 4.5.3)
3, Classification task - random forest and Mushroom dataset
Please refer to section 3 below for the download address and introduction of mushroom dataset
1. c + + code reference
void opencvforest()
{
//Read data
const char* file_name = "D:/Project/deeplearn/dataset/mushroom/agaricus-lepiota.data";
cv::Ptr<TrainData> daraset_forest = TrainData::loadFromCSV(file_name,
0, //Number of lines skipped from the beginning of the data file
0, //The label of the sample starts from this column (that is, the first column is the label)
1, //The sample input eigenvector starts from this column (data from the second column)
"cat[0-22]");
//Validation data
int n_samples = daraset_forest->getNSamples();
int n_features = daraset_forest->getNVars();
cout << "Each sample has" << n_features << "Characteristics" << endl;
if (n_samples == 0)
{
cout << "Error reading file" << file_name << endl;
exit(-1);
}
else
{
cout << "from" << file_name << "In, read" << n_samples << "Samples" << endl;
}
//Divide the training set and test set according to the proportion of 80% and 20%
daraset_forest->setTrainTestSplitRatio(0.8, false);
int n_train_samples = daraset_forest->getNTrainSamples();
int n_test_samples = daraset_forest->getNTestSamples();
cout << "Training samples: " << n_train_samples << endl << "Test samples: " << n_test_samples << endl;
//Create a random forest model
cv::Ptr<RTrees> forest = RTrees::create();
//Set model parameters
forest->setActiveVarCount(0);
forest->setCalculateVarImportance(true);
forest->setTermCriteria(TermCriteria(TermCriteria::MAX_ITER + TermCriteria::EPS, 100, 0.01));
//Training random forest model
cout << "Start training..." << endl;
forest->train(daraset_forest);
cout << "Successful training..." << endl;
//Output attribute importance score
Mat var_importance = forest->getVarImportance();
if (!var_importance.empty())
{
double rt_imp_sum = sum(var_importance)[0];
printf("var#\timportance(%%):\n");
int n = (int)var_importance.total();//Total number of matrix elements
for (int i = 0; i < n; i++)
{
printf("%-2d\t%-4.1f\n",i,100.f * var_importance.at<float>(i) / rt_imp_sum);
}
}
//test
cv::Mat results_train, results_test;
float forest_train_error = forest->calcError(daraset_forest, false, results_train);
float forest_test_error = forest->calcError(daraset_forest, true, results_test);
//Statistical output results
int t = 0, f = 0, total = 0;
cv::Mat expected_responses_forest = daraset_forest->getTestResponses();
//Get test set label
std::vector<cv::String> names_forest;
daraset_forest->getNames(names_forest);
for (int i=0; i< daraset_forest->getNTestSamples(); i++)
{
float responses = results_test.at<float>(i, 0);
float expected = expected_responses_forest.at<float>(i, 0);
cv::String r_str = names_forest[(int)responses];
cv::String e_str = names_forest[(int)expected];
if (responses == expected)
{
t++;
}
else
{
f++;
}
total++;
}
cout << "Correct answer:" << t << endl;
cout << "Wrong answer:" << f << endl;
cout << "Number of test samples:" << total << endl;
cout << "Training dataset error:" << forest_train_error << "%" << endl;
cout << "Test dataset error:" << forest_test_error << "%" << endl;
}The data set division and importance results are output as follows:
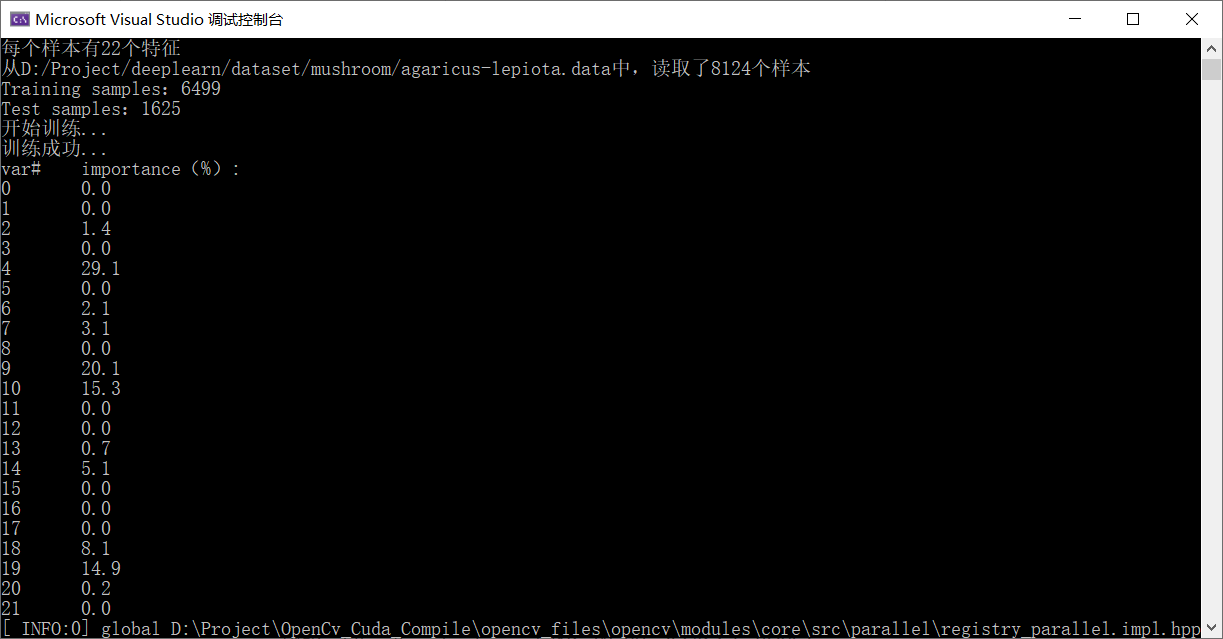
The test results on the test set are as follows:
Correct answer: 1570
Wrong answer: 55
Number of test samples: 1625
Training dataset error: 2.23111%
Test dataset error: 3.38462%
2. c#, opencvsharp code reference
opencvsharp does not partition the data set, so it is better to manually partition the data set by artificial intelligence and open Agaricus Lepiota Data and copy. Here are the first 7000 for training and the last 1124 for testing.
//Organize data and labels
int[,] att = GetTArray(@"D:\mushroom\agaricus-lepiota.handsplit.train.data");
int[] label = GetTLabel(@"D:\mushroom\agaricus-lepiota.handsplit.train.data");
InputArray array = InputArray.Create(att);
InputArray outarray = InputArray.Create(label);
//Create a random forest model and set parameters
OpenCvSharp.ML.RTrees dtrees = OpenCvSharp.ML.RTrees.Create();
dtrees.ActiveVarCount = false;
dtrees.CalculateVarImportance = true;
dtrees.TermCriteria = new TermCriteria(CriteriaType.Eps | CriteriaType.MaxIter, 100, 0.01);
//Stochastic forest model training
dtrees.Train(array, OpenCvSharp.ML.SampleTypes.RowSample, outarray);
//Output attribute importance score
Mat var_importance = dtrees.GetVarImportance();
if (!var_importance.Empty())
{
double rt_imp_sum = Cv2.Sum(var_importance)[0];
int n = (int)var_importance.Total();//Total number of matrix elements
for (int i = 0; i < n; i++)
{
Console.WriteLine(i + ": " + (100f * var_importance.At<float>(i) / rt_imp_sum));
}
}
//test
int t = 0;
int f = 0;
List<int[]> test_arr = GetTestArray(@"D:\mushroom\agaricus-lepiota.handsplit.test.data");
int[] test_label = GetTLabel(@"D:\mushroom\agaricus-lepiota.handsplit.test.data");
for (int i = 0; i < test_arr.Count; i++)
{
Mat p = new Mat(1, 22, OpenCvSharp.MatType.CV_32F, test_arr[i]);
float rrr = dtrees.Predict(p);
//System.Console.WriteLine("" + rrr);
if(test_label[i] == (int)rrr)
{
t++;
}
else
{
f++;
}
}
System.Console.WriteLine("Correct quantity:" + t);
System.Console.WriteLine("Number of errors:" + f);GetTArray, GetLabel read data and other related functions refer to the relevant code in the previous article Opencv learning notes - use opencvsharp and decision tree for training and prediction_ Decision tree decision tree is one of the earliest machine learning algorithms. It originates from the imitation of some human decision-making processes and belongs to supervised learning algorithm. The advantage of decision tree is easy to understand. Some decision trees can be classified or regressed. Two of the top ten data mining algorithms are decision trees [1]. There are many different versions of the decision tree. The typical version is the earliest ID3 algorithm and the improved C4 5 algorithm, these two algorithms can be used for classification. Another branch of improved ID3 algorithm is classification and regression trees (CART) algorithm, which can be used for classification or regression. Cart algorithm is random forest and B https://blog.csdn.net/bashendixie5/article/details/121383341 The output results on the test set are as follows:
https://blog.csdn.net/bashendixie5/article/details/121383341 The output results on the test set are as follows:
Correct quantity: 1117
Number of errors: 7
3. Comparison between decision tree and random forest
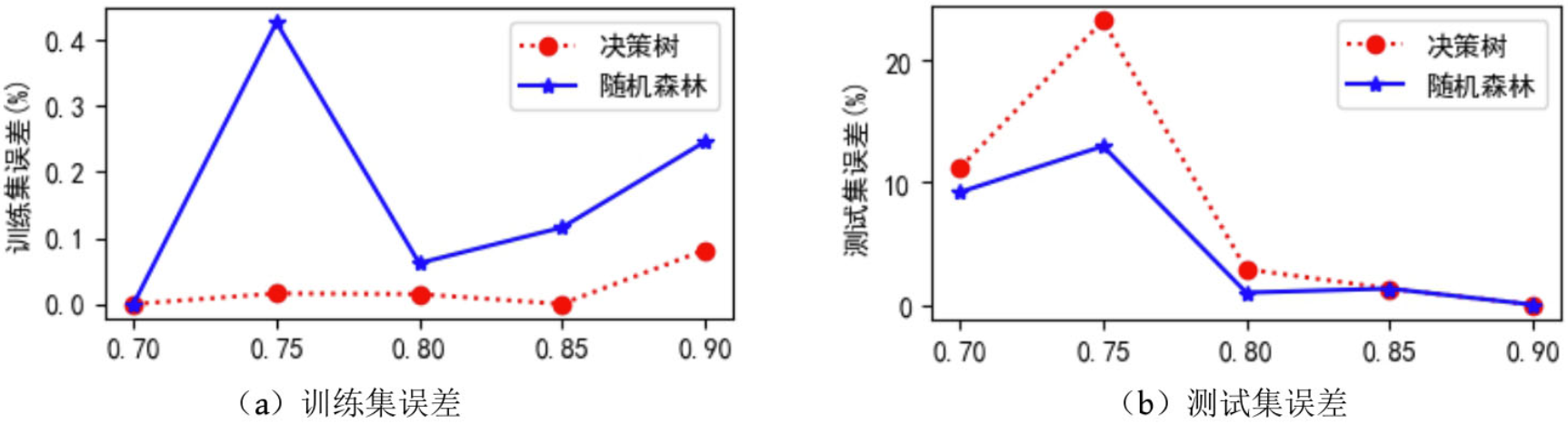
Using decision tree and random forest code respectively, set the division proportion of data set in setTrainTestSplitRatio(0.8, false) method to [0.7, 0.75, 0.8, 0.85, 0.9] respectively to obtain the training set error and test set error of random forest and decision tree on mushroom edible data set under different training data and test data proportion. As shown in the figure below, the training set error of random forest is greater than that of decision tree; The test set error is less than or equal to the test set error of the decision tree. Therefore, it shows that random forest is helpful to reduce the over fitting of the model to the training data. Moreover, no super parameters are set.
4, Regression task - random forest and Boston Housing data sets
The Boston House Price Dataset contains a forecast of house prices in thousands of dollars, given the details of the house and its adjacent houses. The data set is a regression problem. The number of observations in each class is equal, with 506 observations, 13 input variables and 1 output variable.
Boston dataset download address:
Link: https://pan.baidu.com/s/1KwWq32xjJLGKZvLa8C9kJg
Extraction code: c4t0
You can manually split the training dataset (housing train. CSV) and the test dataset (housing test. CSV) using a text editor. The training data set contains 451 samples and the test data set contains 55 samples. The prediction accuracy of random forest is evaluated by root mean square error (RMSE) and mean square error (MSE).
Note: there is missing data in the dataset by default. Please delete or estimate the replacement data by yourself.
When you open a dataset, you can understand the corresponding real meaning according to the header of the first row.
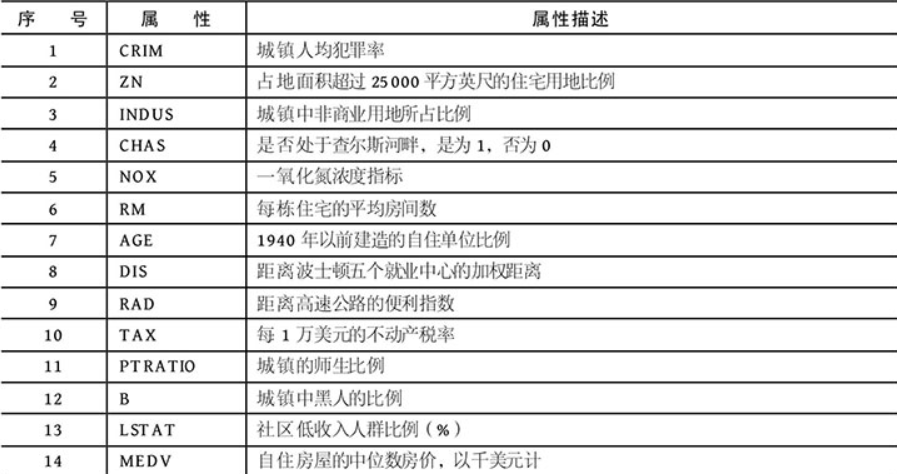
1. c + + code reference
//Read data
const char* file_name = "D:/Project/deeplearn/dataset/boston_housing/train_data.csv";
cv::Ptr<TrainData> daraset_forest = TrainData::loadFromCSV(file_name,
0, //Number of lines skipped from the beginning of the data file
-1, //That is, the last column is the label
-1);//When it is - 1, that is, the last column is the label, which is the column where the previous parameter is located
//Create a random forest model
cv::Ptr<RTrees> forest = RTrees::create();
//Set model parameters
forest->setActiveVarCount(0);
forest->setCalculateVarImportance(true);
forest->setTermCriteria(TermCriteria(TermCriteria::MAX_ITER + TermCriteria::EPS, 100, 0.01));
//Training random forest model
cout << "Start training..." << endl;
forest->train(daraset_forest);
cout << "Successful training..." << endl;
//Output attribute importance score
Mat var_importance = forest->getVarImportance();
if (!var_importance.empty())
{
double rt_imp_sum = sum(var_importance)[0];
printf("var#\timportance(%%):\n");
int n = (int)var_importance.total();//Total number of matrix elements
for (int i = 0; i < n; i++)
{
printf("%-2d\t%-4.1f\n", i, 100.f * var_importance.at<float>(i) / rt_imp_sum);
}
}
//Training set accuracy
cv::Mat results_train;
float MSE_train = forest->calcError(daraset_forest, false, results_train);
//Statistical output results
int total = 0;
cv::Mat expected_responses = daraset_forest->getResponses();
float square_error = 0.0;
for (int i = 0; i < expected_responses.rows; i++)
{
float responses = results_train.at<float>(i, 0);
float expected = expected_responses.at<float>(i, 0);
square_error += (expected - responses) * (expected - responses);
total++;
}
//Calculate RMSE index
float RMSE_train = sqrt(square_error/ total);
forest->save("trained_forest.xml");
cout << "trained mse: " << MSE_train << endl;
cout << "trained rmse: " << RMSE_train << endl;2. c#. opencvsharp code reference
There is no demo implementation of opencvsharp here. You can refer to the opencvsharp code of the mushroom dataset above.