☘ preface ☘

Today is the second day of the zero basis clock out of the algorithm. Today's problem is deadly -. -. Link on:
Series of lecture 100 on the basis of zero algorithm (Lecture 2)

🧑🏻 About the author: a young man who changed from industrial design to embedded
✨ Contact: 2201891280(QQ)
⏳ Approximate reading time of the full text: 20min

🎁 Main knowledge points

1. Arithmetic sequence

The summation formula of arithmetic sequence is n*(n-1)/2

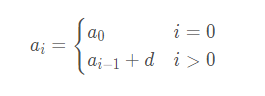
2. Proportional series

The summation formula of proportional sequence is
q 0 ∗ ( 1 − q n ) / ( 1 − q ) q_0*(1-q^n)/(1-q) q0​∗(1−qn)/(1−q)

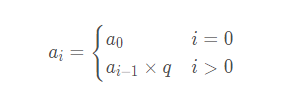
3. Fibonacci series

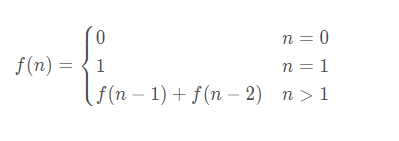
📓 After class exercises

509. Fibonacci number

509. Fibonacci number

Fibonacci numbers are usually represented by F(n), and the sequence formed is called Fibonacci sequence. The sequence starts with 0 and 1, and each subsequent number is the sum of the first two numbers. That is:

F(0) = 0，F(1) = 1
F(n) = F(n - 1) + F(n - 2)，among n > 1

Here you are n, please calculate F(n).

Problem solving ideas

To speed up, save the calculated results and update the values from front to back.

int Fib[31];
int fib(int n){
    Fib[0] = 0;
    Fib[1] = 1;
    for(int i = 2;i <= n;i++)
        Fib[i] = Fib[i-1] + Fib[i-2];
    return Fib[n];
}

1137. N th teponacci number

1137. N th teponacci number

The teponacci sequence Tn is defined as follows:
T0 = 0, T1 = 1, T2 = 1, and Tn+3 = Tn + Tn+1 + Tn+2 when n > = 0
Here is the integer n, please return the value of the nth teponacci number Tn.

Problem solving ideas

What's the difference with the one above? 0.0

int a[38];
int tribonacci(int n){
    a[0] = 0;a[1] = 1;a[2] = 1;
    for(int i =3;i <= n;i++ )
        a[i] = a[i-1] + a[i-2] + a[i-3];
    return a[n];
}

Sword finger Offer 64 Find 1 + 2 +... + n

Sword finger Offer 64 Find 1 + 2 +... + n

For 1 + 2 +... + n, it is required that keywords such as multiplication and division, for, while, if, else, switch, case and conditional judgment statements (A?B:C) cannot be used.

Problem solving ideas

It seems that recursion is the only thing that can be used?

int sumNums(int n){
    if(n == 1) return 1;
    return n + sumNums(n - 1);
}

896. Monotone sequence

896. Monotone sequence

If the array is monotonically increasing or decreasing, it is monotonic.
If for all I < = J, a [i] < = a [J], array A is monotonically increasing. If for all I < = J, a [i] > = a [J], array A is monotonically decreasing.
Returns true when the given array A is a monotone array, otherwise returns false.

Problem solving ideas

The first two unequal elements select increase or decrease. If there is a violation later, it is directly false

bool isMonotonic(int* nums, int numsSize){
    int flag = 0;
    for(int i = 1;i < numsSize;i++)
        if(nums[i] > nums[i-1])
            if(flag == 0)   flag = 1;
            else if(flag == 2)  return false;
            else flag = 1;
        else if(nums[i] < nums[i - 1])
            if(flag == 0)   flag = 2;
            else if(flag == 1)  return false;
            else flag = 2;
    return true;
}

Sword finger Offer 57 - II Continuous positive sequence with sum s

Sword finger Offer 57 - II Continuous positive sequence with sum s

Enter a positive integer target and output a sequence of consecutive positive integers with a sum of target (at least two numbers).
The numbers in the sequence are arranged from small to large, and different sequences are arranged from small to large according to the first number.

Problem solving ideas

Using double pointers, traverse 1-target/2 to find the solution that meets the conditions.

int** findContinuousSequence(int target, int* returnSize, int** returnColumnSizes){
    (*returnSize) = 0;
    int ** ans = malloc(sizeof(int *)*100);
    (*returnColumnSizes) = malloc(sizeof(int)*100);
    for(int left = 1, right = 2;left <= target/2;){
        int sum = (left + right) * (right - left + 1) /2;
        if(sum == target){	//Save when satisfied
            int temp = right - left +1;
            ans[(*returnSize)] = malloc(sizeof(int)*temp);
            (*returnColumnSizes)[(*returnSize)] = temp;
            for(int i = left;i <= right;i++)
                ans[(*returnSize)][i-left] = i;
            (*returnSize)++;
            left++;
        }
        else if(sum < target)   right++;//When it is small, the big pointer moves to the right
        else left++;//The small pointer moves to the right when it is large
    }
    return ans;
}

829. Summation of continuous integers

829. Summation of continuous integers

Given a positive integer N, how many groups of continuous positive integers satisfy that the sum of all numbers is N?

Problem solving ideas

Assuming that it can be decomposed into (x+1) +... + (x+k), we can get
N = k ∗ ( 2 ∗ x + k + 1 ) 2 ⟹ 2 N = k ∗ ( 2 ∗ x + k + 1 ) N = \frac{k*(2*x + k + 1)}{2} \Longrightarrow 2N = k*(2*x + k + 1) N=2k∗(2∗x+k+1)​⟹2N=k∗(2∗x+k+1)
Further analysis shows that the parity property of k is different from that of the later lump. Assuming 2N = 2a *M, all solutions can be obtained by odd decomposition of M.

• In order to speed up, the odd factor of M can be divided continuously. How many factors + 1 (excluding this result) can produce how many results.
• In order to speed up, only the value of root n is studied. If the last is not 1, there is still the last odd factor 0.0

int consecutiveNumbersSum(int n){
    while((n & 1) == 0) n >>= 1;
    int ans = 1, d = 3;
    while(d * d <= n){
        int e = 0;
        while(n % d == 0){
            n /= d;
            e++;
        }
        ans *= (e + 1);
        d += 2;
    }
    if(n > 1)   ans <<= 1;//That means there's another odd factor
    return ans;
}

📑 Write at the end

Recently, the focus will still be on the algorithm notes. I hope you can come with me. I try to be more efficient. zero