
The game interface is shown in the figure below

Of course, there are many websites that play Sudoku games. Now let's take this website as an example. I hope to use Python to realize automatic calculation and fill in Sudoku games!
Maybe the effect can be like this 👇
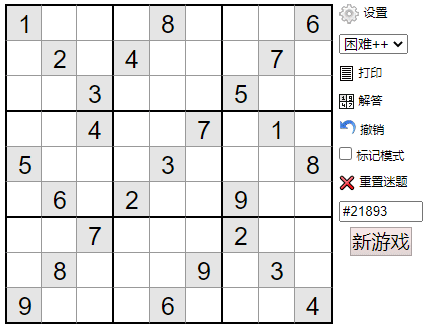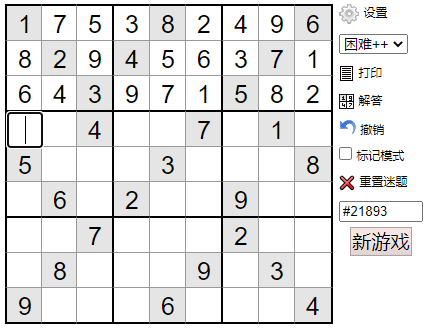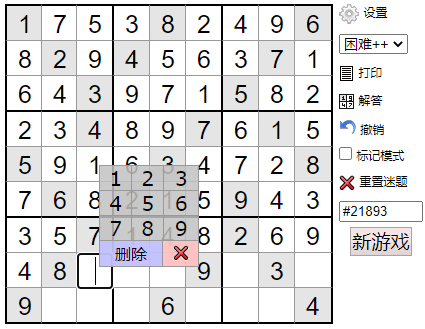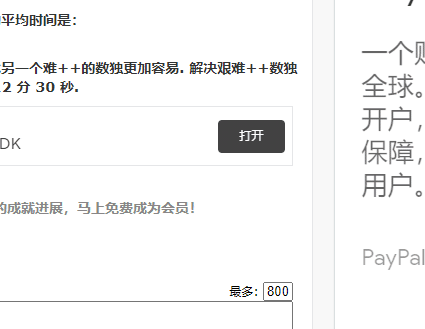
Everyone who has played Sudoku knows the basic rules of Sudoku:
- The numbers 1-9 can only appear once in each line.
- The numbers 1-9 can only appear once in each column.
- The numbers 1-9 can only appear once in each 3x3 uterus separated by a thick solid line.
How can the program help us play this Sudoku game?
Idea:
- We can open the web page through a web automated testing tool, such as selenium
- Parsing web pages to obtain table data
- Auto parse table in incoming handler
- Use the program to automatically write the calculated Sudoku results
Let's try to solve this problem step by step:
Access the target web site through Selenium
For selenium installation, refer to:
https://blog.csdn.net/as60404...
First open the viewer through selenium:
from selenium import webdriver browser = webdriver.Chrome()
If your selenium is installed correctly, running the above code will open Google Explorer:
At this time, we can directly enter the url in the controlled tour, or use the code to control the tour to access the website of Sudoku game:
url = "https://www.sudoku.name/index.php?ln=cn&puzzle_num=&play=1&difficult=4&timer=&time_limit=0" browser.get(url)
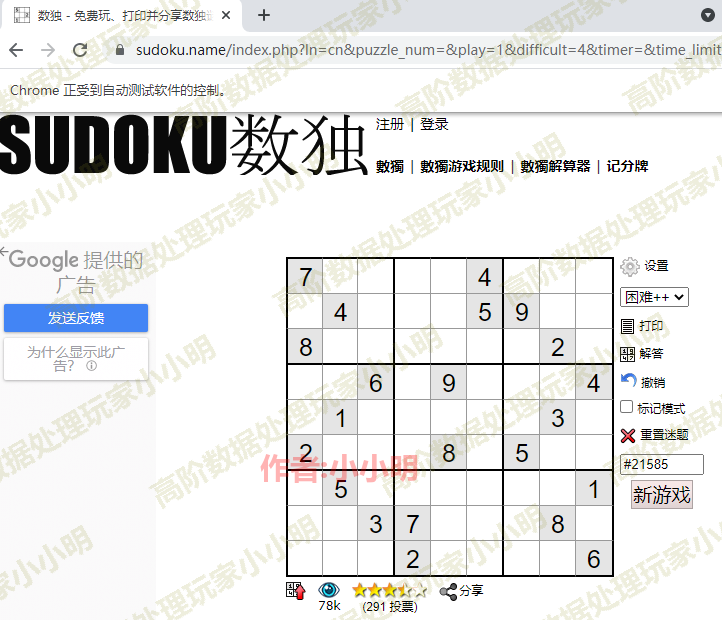
Inner PS: in the future, we still have to install a plug-in for advertising on Google viewer
Sudoku data extraction
Node analysis
The id of the table node is:
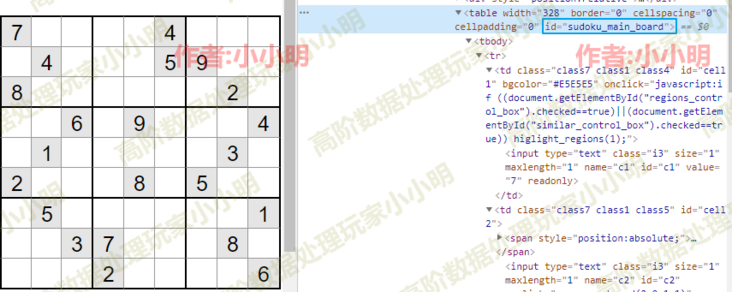
The node value exists in the value attribute:
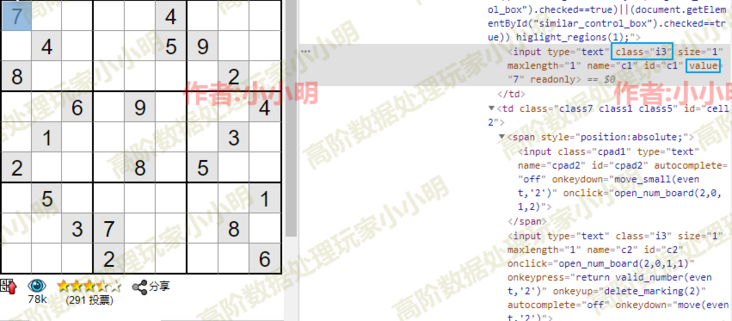
The advantage of using Selenium to control the viewer is that it can let the program extract the data we need at any time.
First get the target table tag:
from selenium.webdriver.common.by import By
from selenium.webdriver.support.ui import WebDriverWait
from selenium.webdriver.support import expected_conditions as EC
wait = WebDriverWait(browser, 10)
table = wait.until(EC.element_to_be_clickable(
(By.CSS_SELECTOR, 'table#sudoku_main_board'))) Next, we extract the Sudoku data we need according to the analysis of nodes:
board = []
for tr in table.find_elements_by_xpath(".//tr"):
row = []
for input_e in tr.find_elements_by_xpath(".//input[@class='i3']"):
cell = input_e.get_attribute("value")
row.append(cell if cell else ".")
board.append(row)
board [['7', '.', '.', '.', '.', '4', '.', '.', '.'], ['.', '4', '.', '.', '.', '5', '9', '.', '.'], ['8', '.', '.', '.', '.', '.', '.', '2', '.'], ['.', '.', '6', '.', '9', '.', '.', '.', '4'], ['.', '1', '.', '.', '.', '.', '.', '3', '.'], ['2', '.', '.', '.', '8', '.', '5', '.', '.'], ['.', '5', '.', '.', '.', '.', '.', '.', '1'], ['.', '.', '3', '7', '.', '.', '.', '8', '.'], ['.', '.', '.', '2', '.', '.', '.', '.', '6']]
Use all the positions that need to be filled in express.
Sudoku calculation program
How to let the program calculate the results for the above Sudoku? This requires the thinking of logical algorithm.
The most basic problem-solving thinking of this kind of problem is to traverse all possible filling methods through recursion + backtracking algorithm to verify the effectiveness one by one until no conflict is found. In the process of recursion, if the current blank cell cannot fill in any number, it will be backtracked.
On this basis, we can use bit operation for optimization. In the conventional method, we need to use an array with a length of 99 to indicate whether each number has occurred. With the help of bit operation, we can use only one integer to indicate whether each number has occurred. For example, the binary table (011000100) indicates that the numbers 3, 7 and 8 have appeared.
Specifically, the final program is quite complex. If you can't understand the code logic, you can copy and paste it directly:
def solveSudoku(board):
def flip(i: int, j: int, digit: int):
line[i] ^= (1 << digit)
column[j] ^= (1 << digit)
block[i // 3][j // 3] ^= (1 << digit)
def dfs(pos: int):
nonlocal valid
if pos == len(spaces):
valid = True
return
i, j = spaces[pos]
mask = ~(line[i] | column[j] | block[i // 3][j // 3]) & 0x1ff
while mask:
digitMask = mask & (-mask)
digit = bin(digitMask).count("0") - 1
flip(i, j, digit)
board[i][j] = str(digit + 1)
dfs(pos + 1)
flip(i, j, digit)
mask &= (mask - 1)
if valid:
return
line = [0] * 9
column = [0] * 9
block = [[0] * 3 for _ in range(3)]
valid = False
spaces = list()
for i in range(9):
for j in range(9):
if board[i][j] == ".":
spaces.append((i, j))
else:
digit = int(board[i][j]) - 1
flip(i, j, digit)
dfs(0) Then we run:
solveSudoku(board) board
[['7', '2', '9', '3', '6', '4', '1', '5', '8'], ['3', '4', '1', '8', '2', '5', '9', '6', '7'], ['8', '6', '5', '9', '7', '1', '4', '2', '3'], ['5', '3', '6', '1', '9', '2', '8', '7', '4'], ['9', '1', '8', '5', '4', '7', '6', '3', '2'], ['2', '7', '4', '6', '8', '3', '5', '1', '9'], ['6', '5', '2', '4', '3', '8', '7', '9', '1'], ['4', '9', '3', '7', '1', '6', '2', '8', '5'], ['1', '8', '7', '2', '5', '9', '3', '4', '6']]
It can be seen that the program has calculated the result of Sudoku.
However, for data:
[['.', '.', '.', '6', '.', '.', '.', '3', '.'], ['5', '.', '.', '.', '.', '.', '6', '.', '.'], ['.', '9', '.', '.', '.', '5', '.', '.', '.'], ['.', '.', '4', '.', '1', '.', '.', '.', '6'], ['.', '.', '.', '4', '.', '3', '.', '.', '.'], ['8', '.', '.', '.', '9', '.', '5', '.', '.'], ['.', '.', '.', '7', '.', '.', '.', '4', '.'], ['.', '.', '5', '.', '.', '.', '.', '.', '8'], ['.', '3', '.', '.', '.', '8', '.', '.', '.']]
The above algorithm takes up to 17 seconds, so we need to continue to optimize the algorithm:
def solveSudoku(board: list) -> None:
def flip(i: int, j: int, digit: int):
line[i] ^= (1 << digit)
column[j] ^= (1 << digit)
block[i // 3][j // 3] ^= (1 << digit)
def dfs(pos: int):
nonlocal valid
if pos == len(spaces):
valid = True
return
i, j = spaces[pos]
mask = ~(line[i] | column[j] | block[i // 3][j // 3]) & 0x1ff
while mask:
digitMask = mask & (-mask)
digit = bin(digitMask).count("0") - 1
flip(i, j, digit)
board[i][j] = str(digit + 1)
dfs(pos + 1)
flip(i, j, digit)
mask &= (mask - 1)
if valid:
return
line = [0] * 9
column = [0] * 9
block = [[0] * 3 for _ in range(3)]
valid = False
spaces = list()
for i in range(9):
for j in range(9):
if board[i][j] != ".":
digit = int(board[i][j]) - 1
flip(i, j, digit)
while True:
modified = False
for i in range(9):
for j in range(9):
if board[i][j] == ".":
mask = ~(line[i] | column[j] |
block[i // 3][j // 3]) & 0x1ff
if not (mask & (mask - 1)):
digit = bin(mask).count("0") - 1
flip(i, j, digit)
board[i][j] = str(digit + 1)
modified = True
if not modified:
break
for i in range(9):
for j in range(9):
if board[i][j] == ".":
spaces.append((i, j))
dfs(0) Run again:
solveSudoku(board) board

It takes only 3.2 seconds, and the performance is improved a lot.
Optimization idea: if only a unique number can be filled in a blank cell, that is, the corresponding b value and b-1 are bitwise summed to get 0 (that is, only one binary bit in B is 1). At this time, we can determine the number filled in the blank cell without waiting for recursion.
What we need to do next is to fill in the results into the corresponding positions. After all, it's hard to knock by ourselves.
Write results back to the web page
For Selenium, we can simulate a manual click on a button and send a keyboard operation.
Let's go over the table tag again and use click and send_keys method:
for i, tr in enumerate(table.find_elements_by_xpath(".//tr")):
for j, input_e in enumerate(tr.find_elements_by_xpath(".//input[@class='i3']")):
if input_e.get_attribute("readonly") == "true":
continue
input_e.click()
input_e.clear()
input_e.send_keys(board[i][j]) Effect during operation:
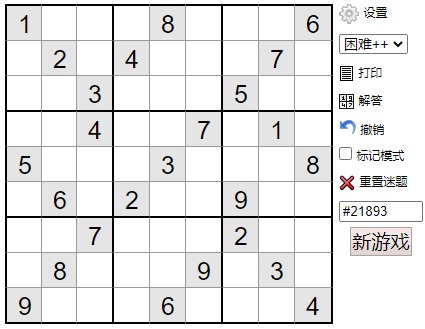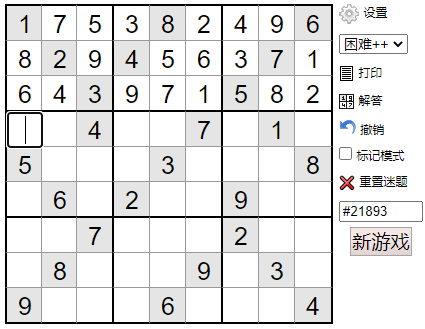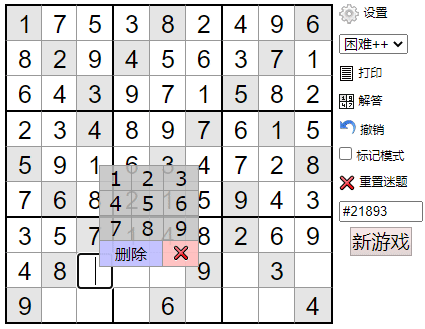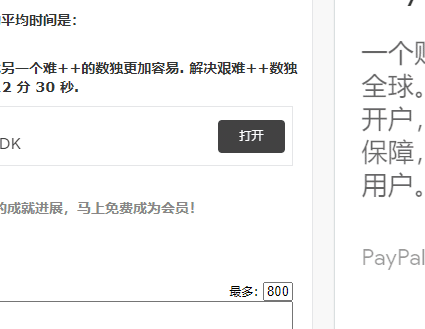
Proof of ashes Sudoku player:

Others 14 minutes, you use the program 10 seconds to complete.
After using Python, I finally experienced the feeling of "the strongest brain". Let me install a B 🚀
end of document
Your favorite collection is my greatest encouragement!
Welcome to follow me, share Python dry goods and exchange Python technology.
If you have any opinions on the article or any technical problems, please leave a message in the comment area for discussion!