What is hash

Hash is used to map a large range of numbers (such as [10 ^ - 9, 109]) to a smaller interval. For example, for 109, we want it to be mapped to the interval [0, 105] (which can also be understood as an array). We can directly remainder 109 (10 ^ 9% 10 ^ 5), and then determine the falling point of the number in the interval according to the remainder. The remainder operation here is called hash, and remainder is also a common hash algorithm.

We use hash to save space. If the memory size is unlimited, we can directly choose to open a piece of 2 * 10 ^ 9 data to store data, but this memory may have many free areas. In practice, the memory is limited. We need to reduce the range of large numbers and gather them together as much as possible. Hash itself is a special discretization.

For the hash table, the efficiency of lookup, insertion and deletion is O(1), which is an expected value (average), which refers to the time complexity when the hash algorithm will not lead to too many conflicts. In the worst case, it is O(n).

Zipper method

Since the scope is reduced, when the amount of data is too large, the remainder will have the same result. At this time, if the landing point is determined according to the remainder, there will be a conflict. There are two solutions: zipper method and open addressing method.

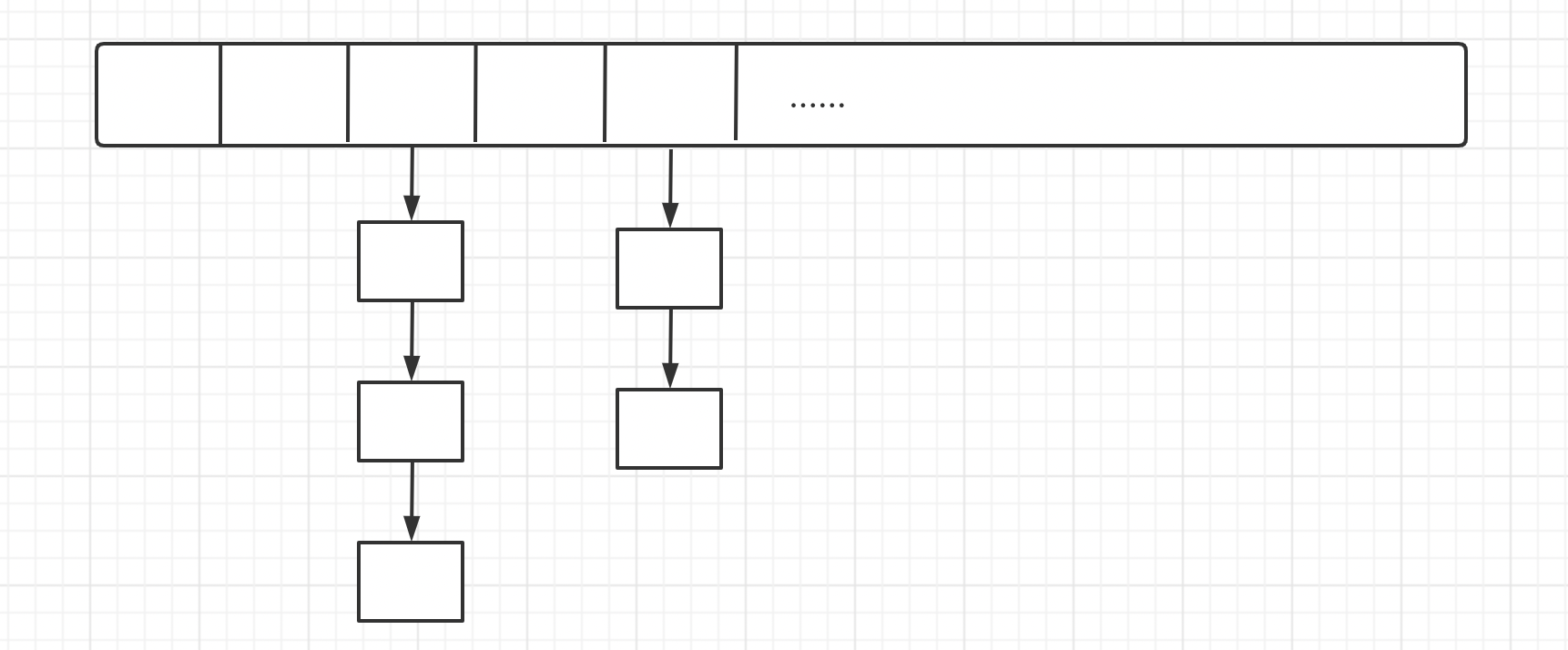
In fact, the zipper method is to extend a linked list at the conflicting points to store the original data with the same remainder. The hash results of all numbers on the chain are the same. When looking for numbers with duplicate hash values, you need to traverse the linked list to see if there is target data.

In fact, we will use balance tree instead of zipper to reduce the search time in conflict.

open addressing

In fact, open addressing method is to find the location backward. When the hash results conflict, if the point on the right is idle, continue to find the location backward until there is an idle point. As long as the hash is over and it is found that the position of the array has been occupied, look back until there is space. On the whole, the hash results in each small section of the array are the same, or the hash results between different cells may be the same, depending on the insertion order.

Concrete implementation

Reference example: Activity - AcWing

Zipper method:

#include<iostream>
#include<cstring>

using namespace std;

const int N = 100003;
int h[N], e[N], ne[N], idx; 

// Find the first prime number larger than 1e5. The mathematical results show that the hash collision probability of the remainder of the prime number is the smallest
// void getN() {
//     for (int i = 100000; ; i ++) {
//         bool flag = false;
//         for (int j = 2; j * j <= i; j ++ ) {
//             if (i % j != 0) {
//                 flag = true;
//             } else {
//                 flag = false;
//                 break;
//             }
//         }
//         if (flag) {
//             cout << i;
//             break;
//         }
//     }
// }

void insert(int x) {
    int k = ((x % N) + N) % N;
    e[idx] = x;
    ne[idx] = h[k];
    h[k] = idx ++;
}

void find(int x) {
    int k = ((x % N) + N) % N;
    for (int i = h[k]; i != - 1; i = ne[i]) {
        if (e[i] == x) {
            cout << "Yes" << endl;
            return;
        }
    }
    cout << "No" << endl;
}

int main() {
    
    // Initialize h[N] to - 1
    memset(h, -1, sizeof h);
    
    int n;
    scanf("%d", &n);
    
    while (n -- ) {
        char op[2]; int x;
        scanf("%s%d", op, &x);
        if (op[0] == 'I') {
            insert(x);
        } else {
            find(x);
        }
    }
    
    return 0;
}

Open addressing:

#include<iostream>
#include<cstring>

using namespace std;

const int N = 100003, null = 0x3f3f3f3f;
int h[N];

void insert(int x) {
    int k = ((x % N) + N) % N;
    while(h[k] != null) {
        k ++;
        if (k == N) k = 0;
    }
    h[k] = x;
}

void find(int x) {
    int k = ((x % N) + N) % N;
    while (h[k] != null) {
        if (h[k] == x) {
            cout << "Yes" << endl;
            return;
        } else {
            k ++;
        }
        if (k == N) k = 0;
    }
    cout << "No" << endl;
}

int main() {
    
    // Initialize h[N] to a number greater than 10 ^ 9, indicating that the location has not been hit
    // For the usage of 0x3f, see: https://www.cnblogs.com/handsomecui/p/4723949.html
    memset(h, 0x3f, sizeof h);
    
    int n;
    scanf("%d", &n);
    
    while (n -- ) {
        char op[2]; int x;
        scanf("%s%d", op, &x);
        if (op[0] == 'I') {
            insert(x);
        } else {
            find(x);
        }
    }
    
    return 0;
}