1, Introduction to ant colony algorithm
1 Overview
An algorithm designed to simulate ant foraging behavior (shortest path principle). The foraging characteristics of ant groups are abstracted and transformed into mathematical description.

• ant colony algorithm (ACA) was first proposed by Marco Dorigo in his doctoral thesis in 1992.
• when looking for food source, ants will release a pheromone on the path they pass through, and can sense the pheromone released by other ants. The size of pheromone concentration indicates the distance of the path. The higher the pheromone concentration, the shorter the corresponding path distance.
• generally, ants will preferentially select the path with high pheromone concentration with a high probability and release a certain amount of pheromone to enhance the pheromone concentration on the path, which will form a positive feedback. Finally, ants can find the best path from the nest to the food source, that is, the shortest distance.
• biologists also found that the pheromone concentration on the path will gradually decline with time.
• the basic idea of applying ant colony algorithm to solve the optimization problem is: the walking path of ants is used to represent the feasible solution of the problem to be optimized, and all paths of the whole ant colony constitute the solution space of the problem to be optimized. The amount of pheromone released by ants with short path is more. With the advance of time, the pheromone concentration accumulated on the short path gradually increases, and the number of ants choosing the path is also more and more. Finally, the whole ant will focus on the best path under the action of positive feedback. At this time, the corresponding is the optimal solution of the problem to be optimized.
Compared with the crossover, selection and mutation of GA (genetic algorithm) and the individual and population extremum optimization of PSO (particle swarm optimization), ant colony algorithm also has its own optimization strategies: positive feedback information mechanism, pheromone concentration update and ant screening of accessible paths.
2 basic ideas
The basic principle of ant colony algorithm comes from the shortest path principle of ant foraging in nature. According to the observation of entomologists, it is found that although the vision of ants in nature is not developed, they can find the shortest path from the food source to the nest without any hint, and can adaptively search the new best path after the environment changes (such as obstacles on the original path). How do ants do this?
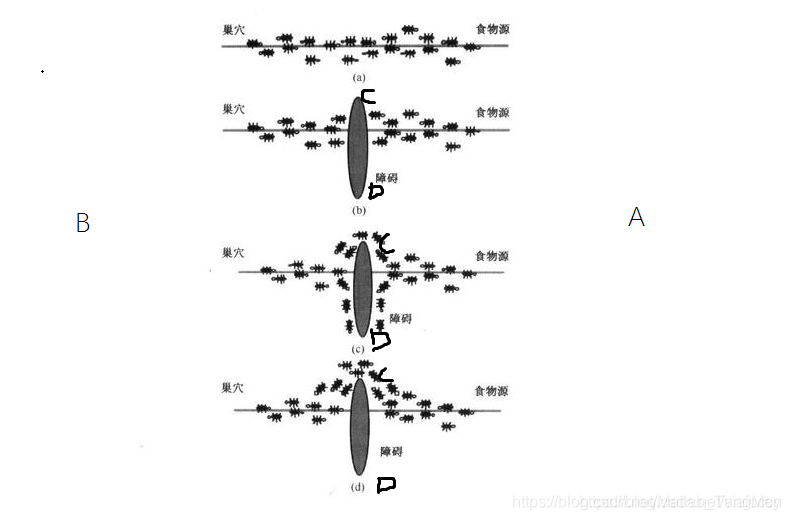
It turns out that when ants are looking for food sources, they can put A pheromone, also known as pheromone, on the path they walk, so that other ants in A certain range can detect it and affect their future behavior. When more and more ants pass through some paths, they leave more and more pheromones, So that the pheromone intensity increases (of course, it will gradually weaken with the passage of time, so the probability of ants choosing the path is higher, which increases the pheromone intensity of the path. This selection process is called the autocatalytic behavior of ants. Because its principle is A positive feedback mechanism, the ant kingdom can also be understood as the so-called enhanced learning system. Here we use A diagram to illustrate ant foraging The shortest path selection principle of is shown in the figure. In, if point A is the nest of ants, point B is food, and there is an obstacle between points A and B, then the ants from point A to point B must decide whether to go left or right, and the ants from point B to point A must also decide which path to take. This decision will be affected by the pheromone concentration (i.e. residual pheromone concentration) left by previous ants on each path. If the pheromone concentration on the right path is relatively large, the right path is more likely to be selected by ants. However, for the first batch of Pathfinder ants, because there is no pheromone influence or the influence is relatively small, they are equally likely to choose left or right, as shown in the figure. With the progress of foraging, the intensity of pheromones on each road began to change, some lines were strong and some lines were weak. Now take the ant from point A to point B as an example to illustrate the change of the subsequent process (the process is basically the same for the ant from point B to point A). Since the path ADB is shorter than the path ACB, the first ant that selects the ADB path reaches point B earlier than the first ant that selects the Acb. At this time, from point B to point A, the pheromone concentration on path BDA is greater than that on path BCA. Therefore, from the next moment, the ants from point B to point A are more likely to choose the BDA path than the BCA path, so that the pheromone on the ABDA route is further enhanced. Therefore, the ants who choose the path according to the pheromone intensity of D gradually prefer the path ADB, as shown in the figure. Over time, almost all ants will choose the path ADB (or BDA) to carry food, and we will also find that the ADB path is actually the shortest path. The principle of ant colony routing can be simply understood as: for A single ant, it has no subjective intention to find the shortest path; But for the whole ant colony system, they do achieve the visual effect of finding the shortest path. In nature, this path finding process of ant colony is A positive feedback process. "Ant colony algorithm" is derived from the principle of simulating ant colony foraging to find the shortest path in biology. For example, we regard the work unit with only simple functions as "ant", then the above process of finding path can be used to explain the optimization process of artificial ant colony in ant colony algorithm. This is the basic idea of ant colony algorithm.
3 flow of algorithm design
Taking TSP problem as an example, the flow of algorithm design is as follows:
Step 1: initialize relevant parameters, including ant colony size, pheromone factor, heuristic function factor, pheromone volatilization factor, pheromone constant, maximum iteration times, etc., read the data into the program and preprocess: for example, convert the coordinate information of cities into the distance matrix between cities.
Step 2: randomly place ants at different starting points, and calculate the next visited city for each ant until an ant has visited all cities.
Step 3: calculate the path length Lk passed by each ant, record the optimal solution of the current number of iterations, and update the pheromone concentration on the path.
Step 4: judge whether the maximum number of iterations has been reached. If not, return to step 2; Yes, end the program.
Step 5: output the results and relevant indicators in the optimization process, such as running time, convergence iteration times, etc.
4 mathematical model



2, Partial source code
function varargout = antinface(varargin)
% ANTINFACE M-file for antinface.fig
% ANTINFACE, by itself, creates a new ANTINFACE or raises the existing
% singleton*.
%
% H = ANTINFACE returns the handle to a new ANTINFACE or the handle to
% the existing singleton*.
%
% ANTINFACE('CALLBACK',hObject,eventData,handles,...) calls the local
% function named CALLBACK in ANTINFACE.M with the given input arguments.
%
% ANTINFACE('Property','Value',...) creates a new ANTINFACE or raises the
% existing singleton*. Starting from the left, property value pairs are
% applied to the GUI before antinface_OpeningFcn gets called. An
% unrecognized property name or invalid value makes property application
% stop. All inputs are passed to antinface_OpeningFcn via varargin.
%
% *See GUI Options on GUIDE's Tools menu. Choose "GUI allows only one
% instance to run (singleton)".
%
% See also: GUIDE, GUIDATA, GUIHANDLES
% Edit the above text to modify the response to help antinface
% Last Modified by GUIDE v2.5 02-Jun-2021 10:29:35
% Begin initialization code - DO NOT EDIT
gui_Singleton = 1;
gui_State = struct('gui_Name', mfilename, ...
'gui_Singleton', gui_Singleton, ...
'gui_OpeningFcn', @antinface_OpeningFcn, ...
'gui_OutputFcn', @antinface_OutputFcn, ...
'gui_LayoutFcn', [] , ...
'gui_Callback', []);
if nargin && ischar(varargin{1})
gui_State.gui_Callback = str2func(varargin{1});
end
if nargout
[varargout{1:nargout}] = gui_mainfcn(gui_State, varargin{:});
else
gui_mainfcn(gui_State, varargin{:});
end
% End initialization code - DO NOT EDIT
% --- Executes just before antinface is made visible.
function antinface_OpeningFcn(hObject, eventdata, handles, varargin)
% This function has no output args, see OutputFcn.
% hObject handle to figure
% eventdata reserved - to be defined in a future version of MATLAB
% handles structure with handles and user state (see GUIDATA)
% varargin command line arguments to antinface (see VARARGIN)
% Choose default command line output for antinface
handles.output = hObject;
% Update handles structure
guidata(hObject, handles);
h=waitbar(0,'Please wait......');
for i=1:100
waitbar(i/100);
end
delete(h);
% UIWAIT makes antinface wait for user response (see UIRESUME)
% uiwait(handles.handles);
% --- Outputs from this function are returned to the command line.
function varargout = antinface_OutputFcn(hObject, eventdata, handles)
% varargout cell array for returning output args (see VARARGOUT);
% hObject handle to figure
% eventdata reserved - to be defined in a future version of MATLAB
% handles structure with handles and user state (see GUIDATA)
% Get default command line output from handles structure
varargout{1} = handles.output;
function edit_initao_Callback(hObject, eventdata, handles)
% hObject handle to edit_initao (see GCBO)
% eventdata reserved - to be defined in a future version of MATLAB
% handles structure with handles and user state (see GUIDATA)
% Hints: get(hObject,'String') returns contents of edit_initao as text
% str2double(get(hObject,'String')) returns contents of edit_initao as a double
% --- Executes during object creation, after setting all properties.
function edit_initao_CreateFcn(hObject, eventdata, handles)
% hObject handle to edit_initao (see GCBO)
% eventdata reserved - to be defined in a future version of MATLAB
% handles empty - handles not created until after all CreateFcns called
% Hint: edit controls usually have a white background on Windows.
% See ISPC and COMPUTER.
if ispc && isequal(get(hObject,'BackgroundColor'), get(0,'defaultUicontrolBackgroundColor'))
set(hObject,'BackgroundColor','white');
end
function edit_q_Callback(hObject, eventdata, handles)
% hObject handle to edit_q (see GCBO)
% eventdata reserved - to be defined in a future version of MATLAB
% handles structure with handles and user state (see GUIDATA)
% Hints: get(hObject,'String') returns contents of edit_q as text
% str2double(get(hObject,'String')) returns contents of edit_q as a double
% --- Executes during object creation, after setting all properties.
function edit_q_CreateFcn(hObject, eventdata, handles)
% hObject handle to edit_q (see GCBO)
% eventdata reserved - to be defined in a future version of MATLAB
% handles empty - handles not created until after all CreateFcns called
% Hint: edit controls usually have a white background on Windows.
% See ISPC and COMPUTER.
if ispc && isequal(get(hObject,'BackgroundColor'), get(0,'defaultUicontrolBackgroundColor'))
set(hObject,'BackgroundColor','white');
end
function edit_alpha_Callback(hObject, eventdata, handles)
% hObject handle to edit_alpha (see GCBO)
% eventdata reserved - to be defined in a future version of MATLAB
% handles structure with handles and user state (see GUIDATA)
% Hints: get(hObject,'String') returns contents of edit_alpha as text
% str2double(get(hObject,'String')) returns contents of edit_alpha as a double
% --- Executes during object creation, after setting all properties.
function edit_alpha_CreateFcn(hObject, eventdata, handles)
% hObject handle to edit_alpha (see GCBO)
% eventdata reserved - to be defined in a future version of MATLAB
% handles empty - handles not created until after all CreateFcns called
% Hint: edit controls usually have a white background on Windows.
% See ISPC and COMPUTER.
if ispc && isequal(get(hObject,'BackgroundColor'), get(0,'defaultUicontrolBackgroundColor'))
set(hObject,'BackgroundColor','white');
end
function edit_rou_Callback(hObject, eventdata, handles)
% hObject handle to edit_rou (see GCBO)
% eventdata reserved - to be defined in a future version of MATLAB
% handles structure with handles and user state (see GUIDATA)
% Hints: get(hObject,'String') returns contents of edit_rou as text
% str2double(get(hObject,'String')) returns contents of edit_rou as a double
% --- Executes during object creation, after setting all properties.
function edit_rou_CreateFcn(hObject, eventdata, handles)
% hObject handle to edit_rou (see GCBO)
% eventdata reserved - to be defined in a future version of MATLAB
% handles empty - handles not created until after all CreateFcns called
% Hint: edit controls usually have a white background on Windows.
% See ISPC and COMPUTER.
if ispc && isequal(get(hObject,'BackgroundColor'), get(0,'defaultUicontrolBackgroundColor'))
set(hObject,'BackgroundColor','white');
end
function edit_beta_Callback(hObject, eventdata, handles)
% hObject handle to edit_beta (see GCBO)
% eventdata reserved - to be defined in a future version of MATLAB
% handles structure with handles and user state (see GUIDATA)
% Hints: get(hObject,'String') returns contents of edit_beta as text
% str2double(get(hObject,'String')) returns contents of edit_beta as a double
% --- Executes during object creation, after setting all properties.
function edit_beta_CreateFcn(hObject, eventdata, handles)
% hObject handle to edit_beta (see GCBO)
% eventdata reserved - to be defined in a future version of MATLAB
% handles empty - handles not created until after all CreateFcns called
% Hint: edit controls usually have a white background on Windows.
% See ISPC and COMPUTER.
if ispc && isequal(get(hObject,'BackgroundColor'), get(0,'defaultUicontrolBackgroundColor'))
set(hObject,'BackgroundColor','white');
end
function edit_ncmax_Callback(hObject, eventdata, handles)
% hObject handle to edit_ncmax (see GCBO)
% eventdata reserved - to be defined in a future version of MATLAB
% handles structure with handles and user state (see GUIDATA)
% Hints: get(hObject,'String') returns contents of edit_ncmax as text
% str2double(get(hObject,'String')) returns contents of edit_ncmax as a double
% --- Executes during object creation, after setting all properties.
function edit_ncmax_CreateFcn(hObject, eventdata, handles)
% hObject handle to edit_ncmax (see GCBO)
% eventdata reserved - to be defined in a future version of MATLAB
% handles empty - handles not created until after all CreateFcns called
% Hint: edit controls usually have a white background on Windows.
% See ISPC and COMPUTER.
if ispc && isequal(get(hObject,'BackgroundColor'), get(0,'defaultUicontrolBackgroundColor'))
set(hObject,'BackgroundColor','white');
end
function edit_antsum_Callback(hObject, eventdata, handles)
% hObject handle to edit_antsum (see GCBO)
% eventdata reserved - to be defined in a future version of MATLAB
% handles structure with handles and user state (see GUIDATA)
% Hints: get(hObject,'String') returns contents of edit_antsum as text
% str2double(get(hObject,'String')) returns contents of edit_antsum as a double
% --- Executes during object creation, after setting all properties.
function edit_antsum_CreateFcn(hObject, eventdata, handles)
% hObject handle to edit_antsum (see GCBO)
% eventdata reserved - to be defined in a future version of MATLAB
% handles empty - handles not created until after all CreateFcns called
% Hint: edit controls usually have a white background on Windows.
% See ISPC and COMPUTER.
if ispc && isequal(get(hObject,'BackgroundColor'), get(0,'defaultUicontrolBackgroundColor'))
set(hObject,'BackgroundColor','white');
end
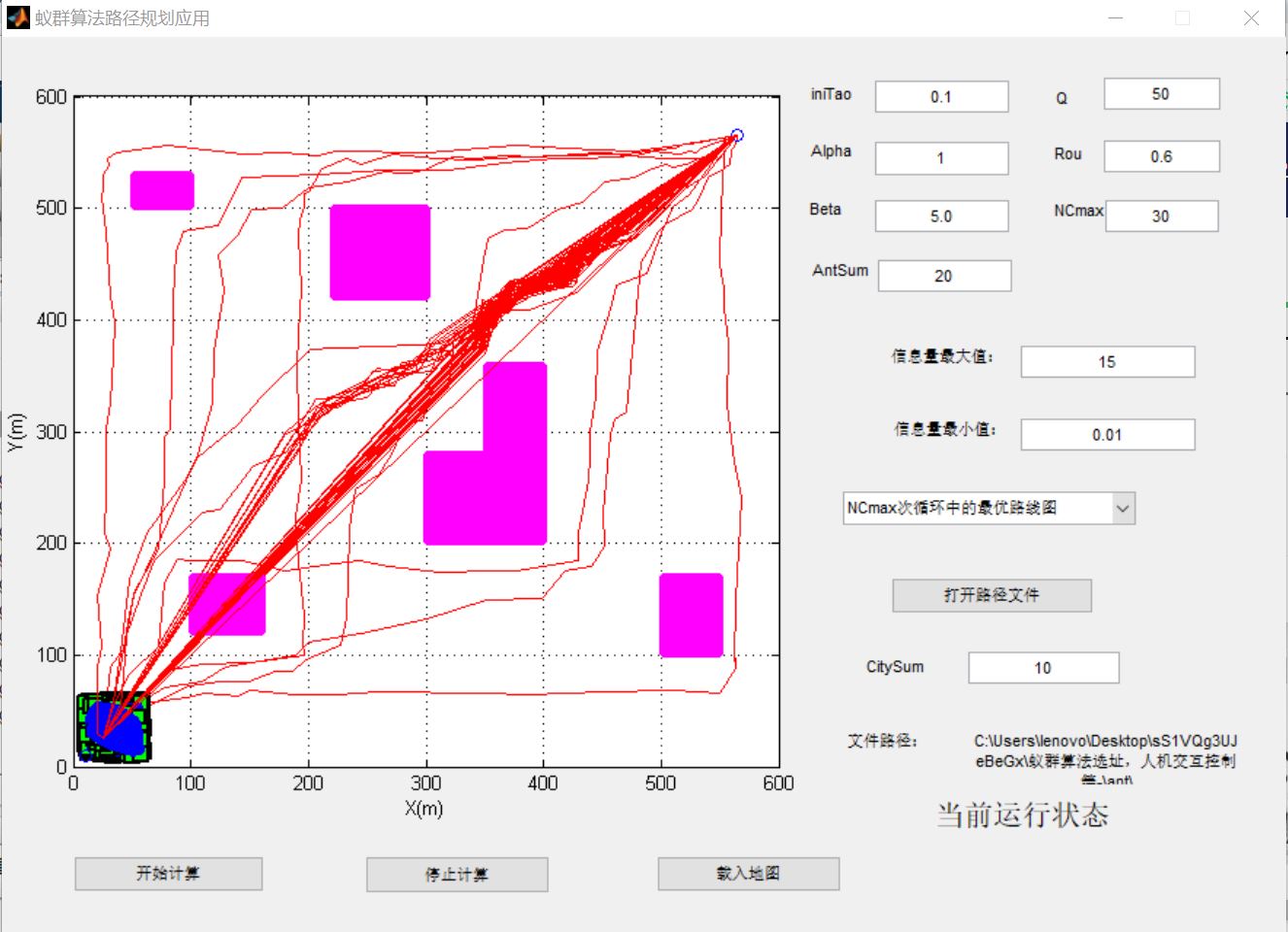
3, Operation results
4, matlab version and references
1 matlab version
2014a
2 references
[1] Steamed stuffed bun Yang, Yu Jizhou, Yang Shan Intelligent optimization algorithm and its MATLAB example (2nd Edition) [M]. Electronic Industry Press, 2016
[2] Zhang Yan, Wu Shuigen MATLAB optimization algorithm source code [M] Tsinghua University Press, 2017