SET key2 value2
OK
MGET key1 key2 key3 # returns a list

1. "value1"
2. "value2"
3. (nil)

MSET key1 value1 key2 value2
MGET key1 key2

1. "value1"
2. "value2"

#### ⑤ , expiration, and SET command extensions
 Yes key Set the expiration time, and the expiration time will be automatically deleted. This function is often used to control the expiration time of the cache.(**Expiration can be any data structure**)
```java
> SET key value1 
> GET key 
"value1" 
> EXPIRE name 5 # Expires after 5s 
... # Wait for 5s 
> GET key 
(nil)

SETEX command equivalent to set + Express:

> SETEX key 5 value1 
... # Wait for 5s to obtain 
> GET key 
(nil) 

> SETNX key value1 		# If the key does not exist, SET succeeds 
(integer) 1 
> SETNX key value1 		# If the key exists, SET fails 
(integer) 0 
> GET key 
> "value" 				# No change

⑥ , counting

If value is an integer, you can also use the INCR command to perform atomic auto increment operation on it, which means that multiple customers can operate on the same key in time, which will never lead to competition:

> SET counter 100 
> INCR counter 
(integer) 101 
> INCRBY counter 50 
(integer) 151

⑦ . GETSET command that returns the original value

For strings, there is another interesting GETSET. Its function is the same as its name: set a value for the key and return the original value:

> SET key value 
> GETSET key value1 
"value"

This is convenient for setting and viewing some keys that need to be counted at intervals. For example, whenever the system is entered by the user, you use the INCR command to operate a key. When statistics are needed, you use the GETSET command to re assign the key to 0, so as to achieve the purpose of statistics.

2) List list

Redis's list is equivalent to LinkedList in Java language. Note that it is a linked list rather than an array. This means that the insertion and deletion operations of the list are very fast, with a time complexity of O(1), but the index positioning is very slow, with a time complexity of O(n).

We can start from the source adlist H / listnode to see its definition:

/* 
Node, List, and Iterator are the only data structures used currently. */

typedef struct listNode { 
	struct listNode *prev; 
	struct listNode *next; 
	void *value; 
} listNode; 

typedef struct listIter { 
	listNode *next; 
	int direction; 
} listIter;

typedef struct list { 
	listNode *head; 
	listNode *tail; 
	void *(*dup)(void *ptr); 
	void (*free)(void *ptr); 
	int (*match)(void *ptr, void *key); 
	unsigned long len; 
} list;

It can be seen that multiple LISTNODES can form a two-way linked list through prev and next pointers:

Although only multiple listNode structures can be used to form a linked list, adlist If you use the H / list structure to hold the linked list, it will be more convenient to operate:

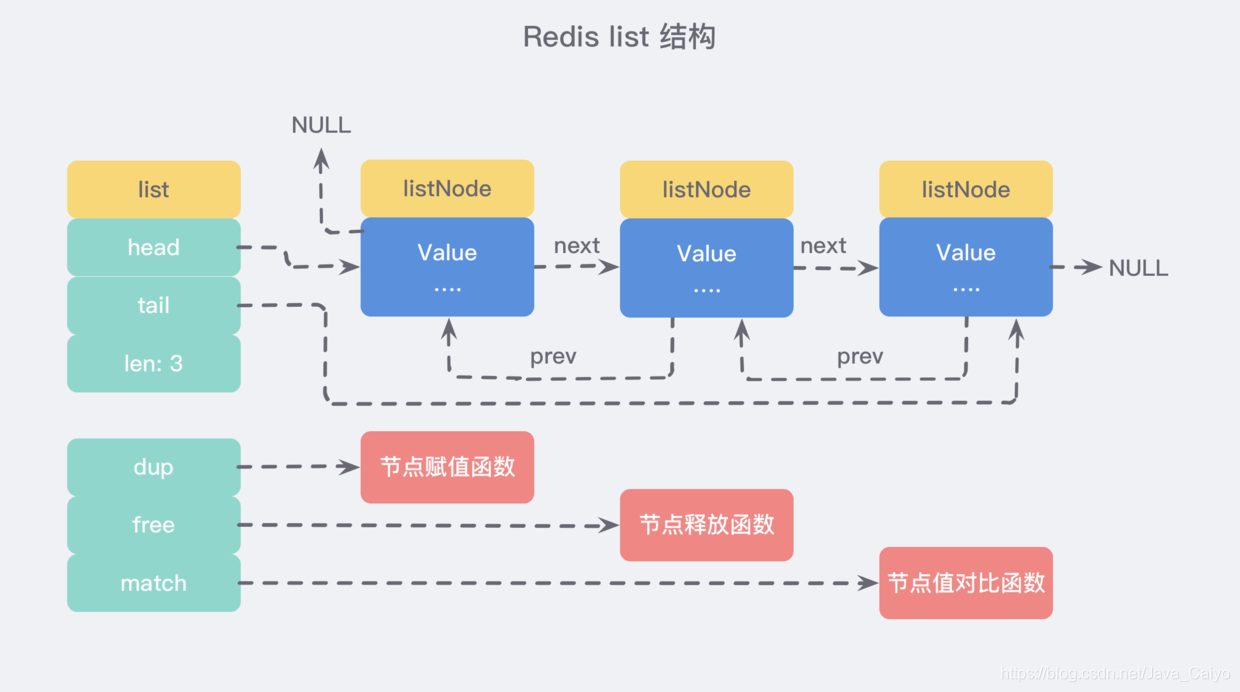
① Basic operation of linked list

• LPUSH and RPUSH can add a new element to the left (head) and right (tail) of the list respectively;
• The LRANGE command can extract a certain range of elements from the list;
• The LINDEX command can extract the elements of the specified table from the list, which is equivalent to the get(int index) operation in the Java linked list operation;

Demonstration:

> rpush mylist A 
(integer) 1 
> rpush mylist B 
(integer) 2 
> lpush mylist first 
(integer) 3 
> lrange mylist 0 -1 # -1 represents the penultimate element. Here, it represents all elements from the first element to the last element
1) "first" 
2) "A" 
3) "B"

② list implementation queue

Queue is a first in first out data structure, which is often used for message queuing and asynchronous logical processing. It will ensure the access order of elements:

> RPUSH books python java golang 
(integer) 3 
> LPOP books 
"python" 
> LPOP books 
"java" 
> LPOP books 
"golang" 
> LPOP books 
(nil)

③ list implementation stack

Stack is a first in and last out data structure, just opposite to queue:

> RPUSH books python java golang 
> RPOP books 
"golang" 
> RPOP books 
"java" 
> RPOP books 
"python" 
> RPOP books 
(nil)

3) Dictionary hash

The dictionary in Redis is equivalent to the HashMap in Java, and its internal implementation is almost similar. It solves some hash conflicts through the chain address method of "array + linked list". At the same time, this structure also absorbs the advantages of two different data structures. The source code is defined as dict.h/dictht:

typedef struct dictht { 
	// Hash table array 
	dictEntry **table; 
	// Hash table size 
	unsigned long size; 
	// Hash table size mask, used to calculate index value, always equal to size - 1 
	unsigned long sizemask; 
	// The number of existing nodes in the hash table 
	unsigned long used;
} dictht;

typedef struct dict { 
	dictType *type; 
	void *privdata; 
	// There are two dictht structures inside 
	dictht ht[2]; 
	long rehashidx; /* rehashing not in progress if rehashidx == -1 */ 
	unsigned long iterators; /* number of iterators currently running */ 
} dict;

The table attribute is an array. Each element in the array is a pointer to the dict.h/dictEntry structure, and each dictEntry structure holds a key value pair:

typedef struct dictEntry { 
	// key 
	void *key; 
	// value 
	union { 
		void *val; 
		uint64_t u64; 
		int64_t s64; 
		double d; 
	} v; 
	// Point to the next hash table node to form a linked list 
	struct dictEntry *next; 
} dictEntry;

As can be seen from the above source code, in fact, the dictionary structure contains two hashtables. Generally, only one hashtable is valuable. However, when the dictionary is expanded or shrunk, it is necessary to allocate a new hashtable and then move it gradually (the reasons are described below).

① Progressive rehash

The expansion of large dictionaries is time-consuming. It is necessary to re apply for a new array, and then re attach all the elements in the linked list of the old dictionary to the new array. This is an O(n) level operation. As a single thread, Redis can hardly bear such a time-consuming process. Therefore, Redis uses progressive rehash for small-step relocation:

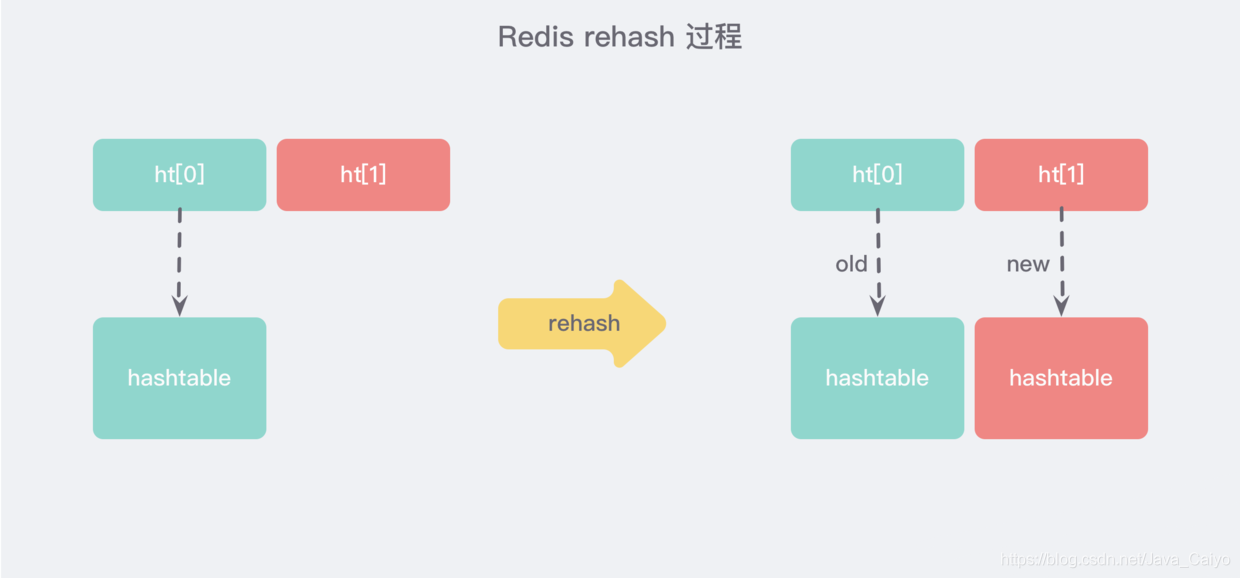
Progressive rehash will retain the old and new hash structures while rehash. As shown in the above figure, two hash structures will be queried at the same time during query, and then the contents of the old dictionary will be gradually migrated to the new dictionary in subsequent scheduled tasks and hash operation instructions. When the relocation is completed, a new hash structure will be used instead.

② Conditions for expansion and contraction

Under normal circumstances, when the number of elements in the hash table is equal to the length of the first dimensional array, it will start to expand. The expanded new array is twice the size of the original array. However, if Redis is doing bgsave (persistence command) and needs too much separation in order to reduce memory, Redis tries not to expand the capacity. However, if the hash table is very full and reaches 5 times the length of the first dimensional array, it will be forced to expand the capacity at this time.

When the hash table becomes more and more sparse because the elements are gradually deleted, Redis will shrink the hash table to reduce the space occupation of the first dimensional array of the hash table. The condition used is that the number of elements is less than 10% of the array length, and whether Redis is doing bgsave will not be considered for volume reduction.

③ Basic operation of dictionary

Hash also has disadvantages. The storage consumption of hash structure is higher than that of a single string. Therefore, whether to use hash or string needs to be weighed again and again according to the actual situation:

> HSET books java "think in java" 		# If the command line string contains spaces, it needs to be wrapped in quotation marks 
(integer) 1 
> HSET books python "python cookbook" 
(integer) 1 
> HGETALL books # The key and value intervals appear 
1) "java" 
2) "think in java" 
3) "python" 
4) "python cookbook" 
> HGET books java 
"think in java" 
> HSET books java "head first java" 
(integer) 0 						# 0 is returned because it is an update operation 
> HMSET books java "effetive java" python "learning python" 		# Batch operation OK

4) Set set

The Redis collection is equivalent to the HashSet in the Java language, and its internal key value pairs are unordered and unique. Its internal implementation is equivalent to a special dictionary. All values in the dictionary are NULL.

① Basic use of set

Since the structure is relatively simple, let's take a look at how it is used:

> SADD books java 
(integer) 1 
> SADD books java			 # repeat 
(integer) 0 
> SADD books python golang 
(integer) 2 
> SMEMBERS books 			# Note the order. set is out of order 
1) "java" 
2) "python" 
3) "golang" 
> SISMEMBER books java 		# Query whether a value exists, which is equivalent to contains 
(integer) 1 
> SCARD books 				# Get length 
(integer) 3 
> SPOP books 				# Pop up a 
"java"

5) zset with sequence table

This may be the most distinctive data structure of Redis. It is similar to the combination of SortedSet and HashMap in Java. On the one hand, it is a set to ensure the uniqueness of internal values. On the other hand, it can give each value a score value to represent the weight of sorting.

Its internal implementation uses a data structure called "jump table". Due to its complexity, it is good to simply mention the principle here:

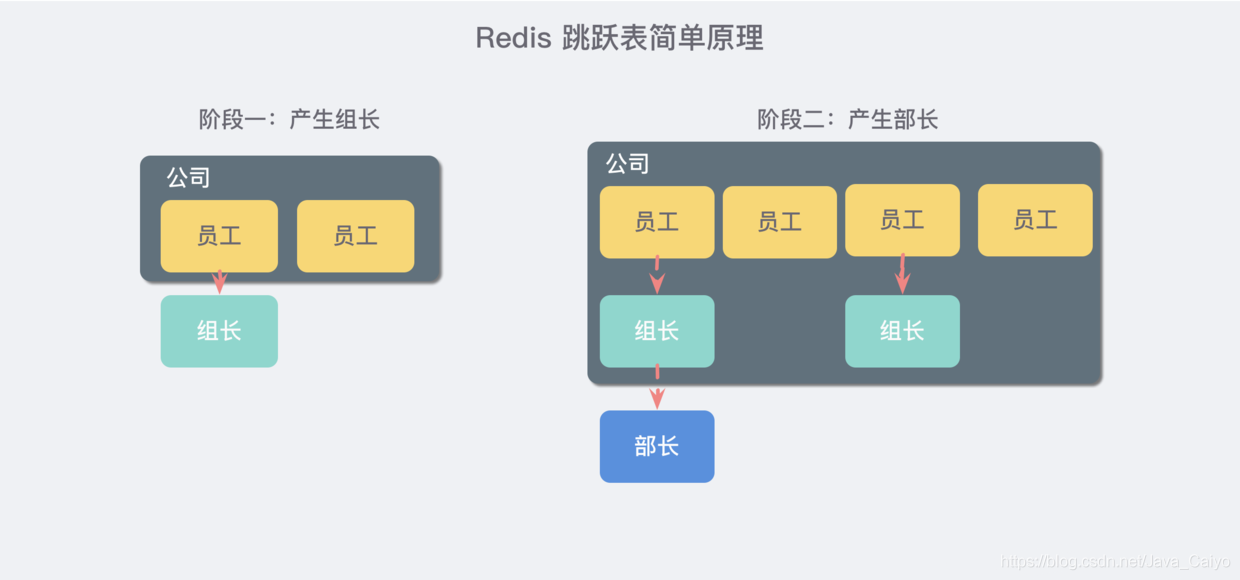
Imagine that you are the boss of a start-up company. At the beginning, there are only a few people, and everyone is on an equal footing. Later, with the development of the company, there were more and more people, and the team communication cost gradually increased. The team leader system was gradually introduced to divide the team, so some people were both employees and team leaders.

Later, the scale of the company further expanded, and the company needs to enter another level: Department. Therefore, each department will elect a minister from the group leader.

The jump table is similar to such a mechanism. All the elements in the lowest layer will be concatenated. They are all employees. Then, a representative will be selected every few elements, and then these representatives will be concatenated with another level of pointer. Then select secondary representatives from these representatives and string them together. Finally formed a pyramid structure.

Think about your current geographical location: Asia > China > a province > a city >... That's such a structure!

① . basic operation of zset with sequence table

> ZADD books 9.0 "think in java" 
> ZADD books 8.9 "java concurrency" 
> ZADD books 8.6 "java cookbook" 

> ZRANGE books 0 -1 # Sort and list by score, and the parameter range is the ranking range 
1) "java cookbook" 
2) "java concurrency" 
3) "think in java" 

> ZREVRANGE books 0 -1 # It is listed in reverse order by score, and the parameter range is the ranking range 
1) "think in java" 
2) "java concurrency" 
3) "java cookbook" 

> ZCARD books # Equivalent to count() 
(integer) 3 

> ZSCORE books "java concurrency" # Gets the score of the specified value 
"8.9000000000000004" # The internal score is stored in double type, so there is a decimal point accuracy problem

> ZRANK books "java concurrency" # ranking 
(integer) 1 

> ZRANGEBYSCORE books 0 8.91 # Traverse zset according to the score interval 
1) "java cookbook" 
2) "java concurrency" 

> ZRANGEBYSCORE books -inf 8.91 withscores # Traverse zset according to the score interval (- ∞, 8.91] and return the score. inf stands for infinite. 
1) "java cookbook" 
2) "8.5999999999999996" 
3) "java concurrency" 
4) "8.9000000000000004" 

> ZREM books "java concurrency" # Delete value 
(integer) 1 
> ZRANGE books 0 -1 
1) "java cookbook" 
2) "think in java"

2, Jump table

1. Introduction to jump table

Skip list is a randomized data structure, which was proposed by William Pugh in his paper Skip lists: a probabilistic alternative to balanced trees. It is a hierarchical linked list structure comparable to the balanced tree - operations such as finding, deleting and adding can be completed in logarithmic expected time. The following is a typical example of a skip list:

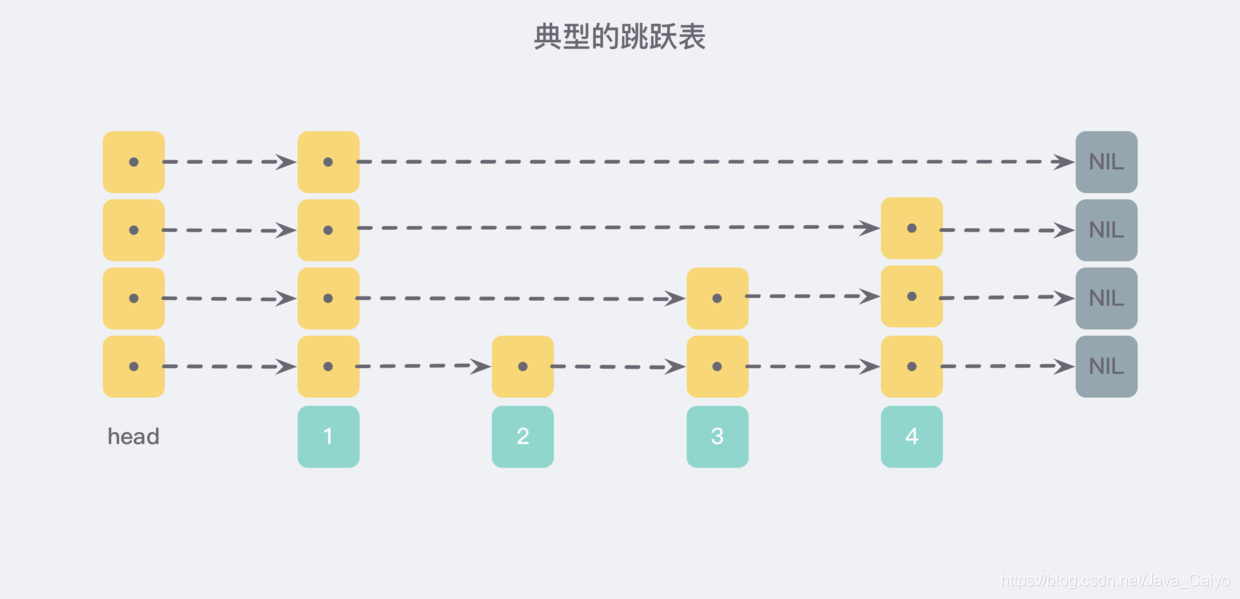
In the previous article, we mentioned that among the five basic structures of Redis, there is a data structure called zset with sequence table, which is similar to the combination of SortedSet and HashMap in Java. On the one hand, it is a set that ensures the uniqueness of internal values, and on the other hand, it can give each value a sorting weight value score to achieve the purpose of sorting.

Its internal implementation relies on a data structure called * * jump list * *.

1) Why use jump tables

First of all, because zset supports random insertion and deletion, it is not suitable to use arrays to implement it. As for sorting, we can easily think of tree structures such as red black tree / balanced tree. Why doesn't Redis use such structures?

1. Performance considerations: in the case of high concurrency, the tree structure needs to perform some operations similar to rebalance, which may involve the whole tree. Relatively speaking, the change of the jump table only involves parts (described in detail below);
2. Implementation considerations: when the complexity is the same as that of red black tree, the implementation of jump table is simpler and more intuitive;

Based on the above considerations, Redis adopts the structure of jump table after making some improvements based on William Pugh's paper.

2) The essence is to solve the problem

Let's first look at a common linked list structure:

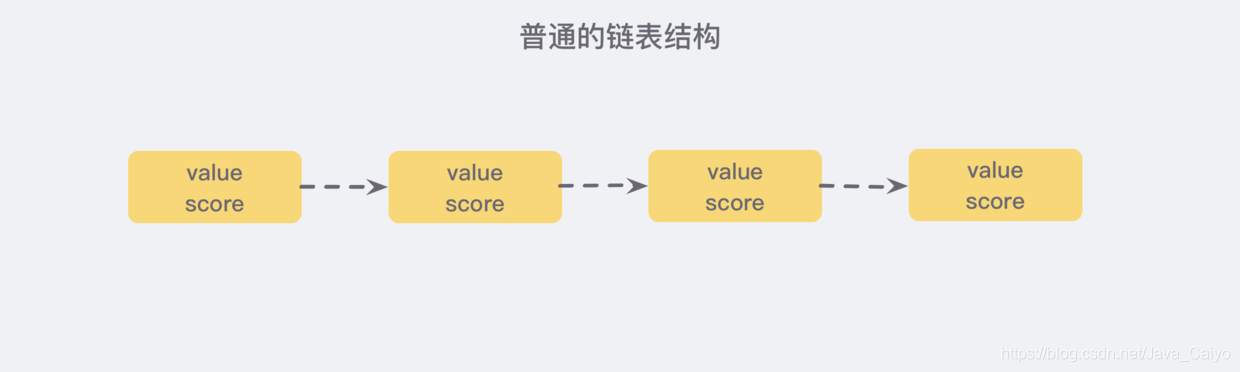
We need to sort the linked list according to the score value, which means that when we need to add new elements, we need to locate the insertion point, so as to continue to ensure that the linked list is orderly. Usually, we use the binary search method, but the binary search has an ordinal group, and the linked list cannot locate the position, There seems to be no better way for us to traverse the whole and find the first node larger than the given data (time complexity O(n)).

However, if we add a pointer between every two adjacent nodes to point to the next node, as shown in the following figure:

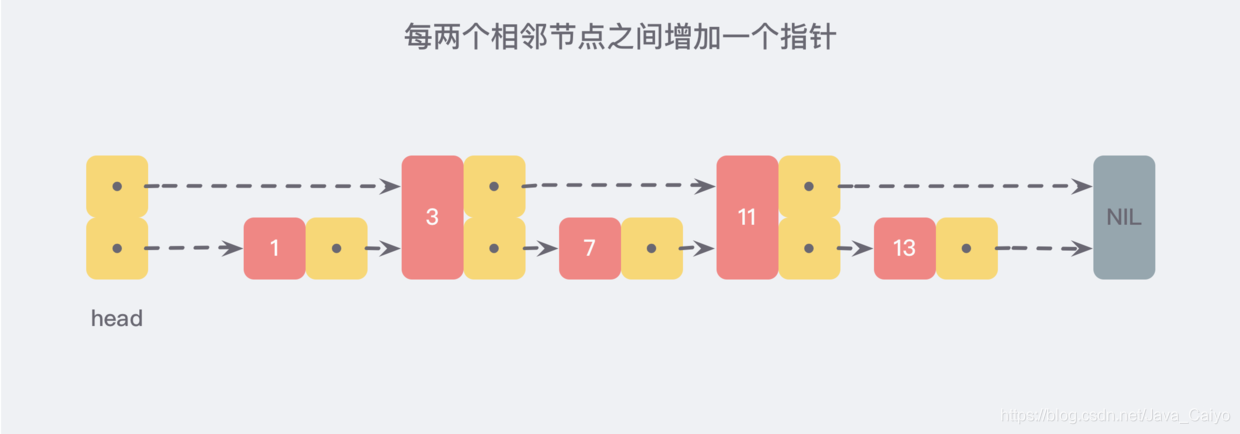
In this way, all new pointers are connected into a new linked list, but it contains only half of the original data (3 and 11 in the figure).

Now let's assume that when we want to find data, we can find it according to this new linked list. If we encounter a node larger than the data to be found, we can go back to the original linked list for search. For example, we want to find 7, and the search path is along the direction pointed by the red pointer marked in the figure below:

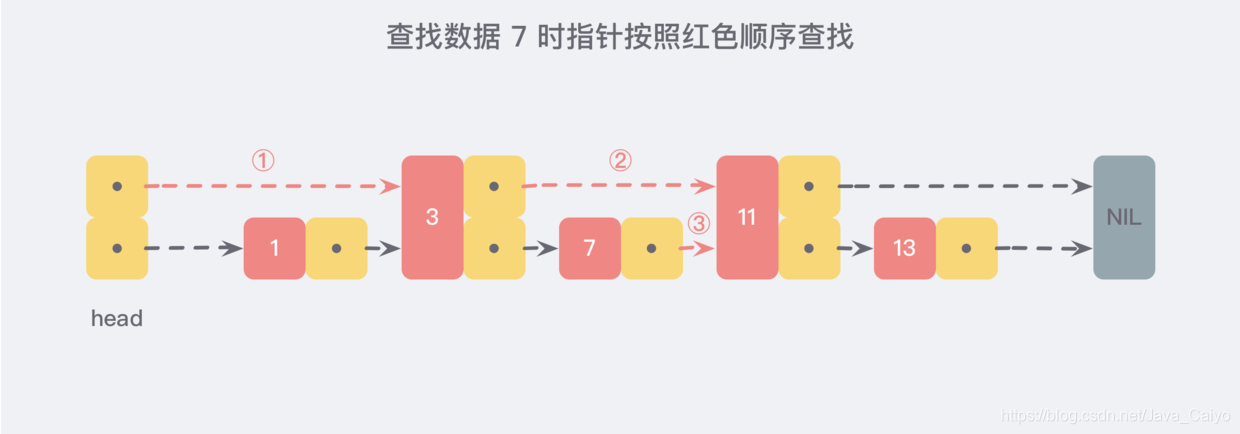
This is a slightly extreme example, but we can still see that through the newly added pointer search, we no longer need to compare each node on the linked list one by one. In this way, the number of nodes to be compared after improvement is about half of the original.

In the same way, we can continue to add a pointer to every two adjacent nodes on the newly generated linked list to generate the third layer linked list:

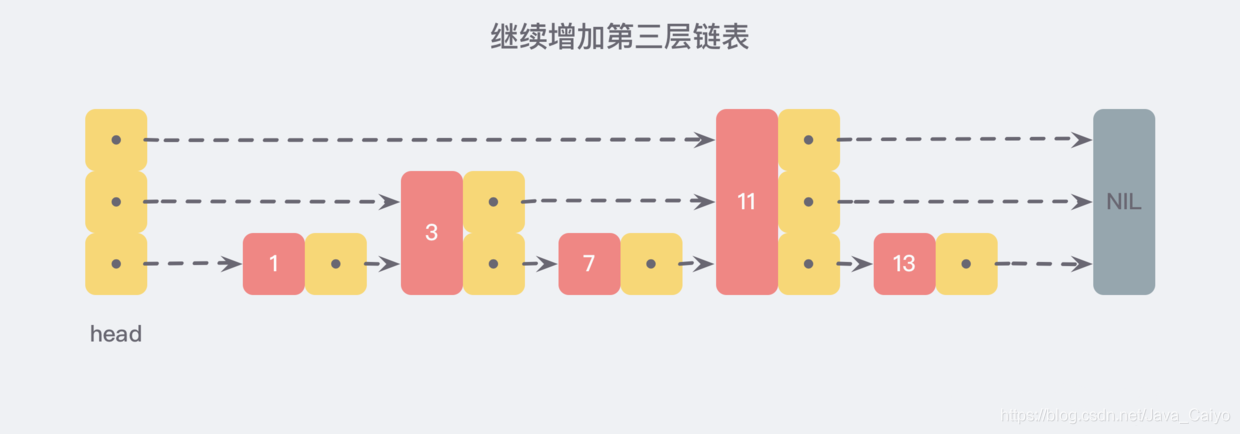
In this new three-tier linked list structure, we try to find 13. The first comparison along the top-level linked list is 11. It is found that 11 is smaller than 13, so we know that we only need to continue searching after 11, so we skip all the nodes in front of 11 at once.

It is conceivable that when the linked list is long enough, such a multi-layer linked list structure can help us skip many lower nodes, so as to speed up the efficiency of search.

3) Further jump table

The skip list is inspired by this multi-layer linked list structure. According to the method of generating the linked list above, the number of nodes in each layer of the linked list above is half the number of nodes in the lower layer. In this way, the search process is very similar to a binary search, so that the time complexity of the search can be reduced to O(logn).

However, this method has great problems in inserting data. After a new node is inserted, the strict 2:1 correspondence of the number of nodes in the upper and lower adjacent linked lists will be disrupted. If you want to maintain this correspondence, you must readjust all the nodes behind the newly inserted nodes (including the newly inserted nodes), which will degenerate the time complexity into O(n). Deleting data has the same problem.

In order to avoid this problem, skiplist does not require strict correspondence between the number of nodes in the upper and lower adjacent linked lists, but randomly selects a level for each node. For example, if the random number of layers of a node is 3, it is linked to the three-layer linked list from layer 1 to layer 3. For clarity, the following figure shows how to form a skiplist through step-by-step insertion:

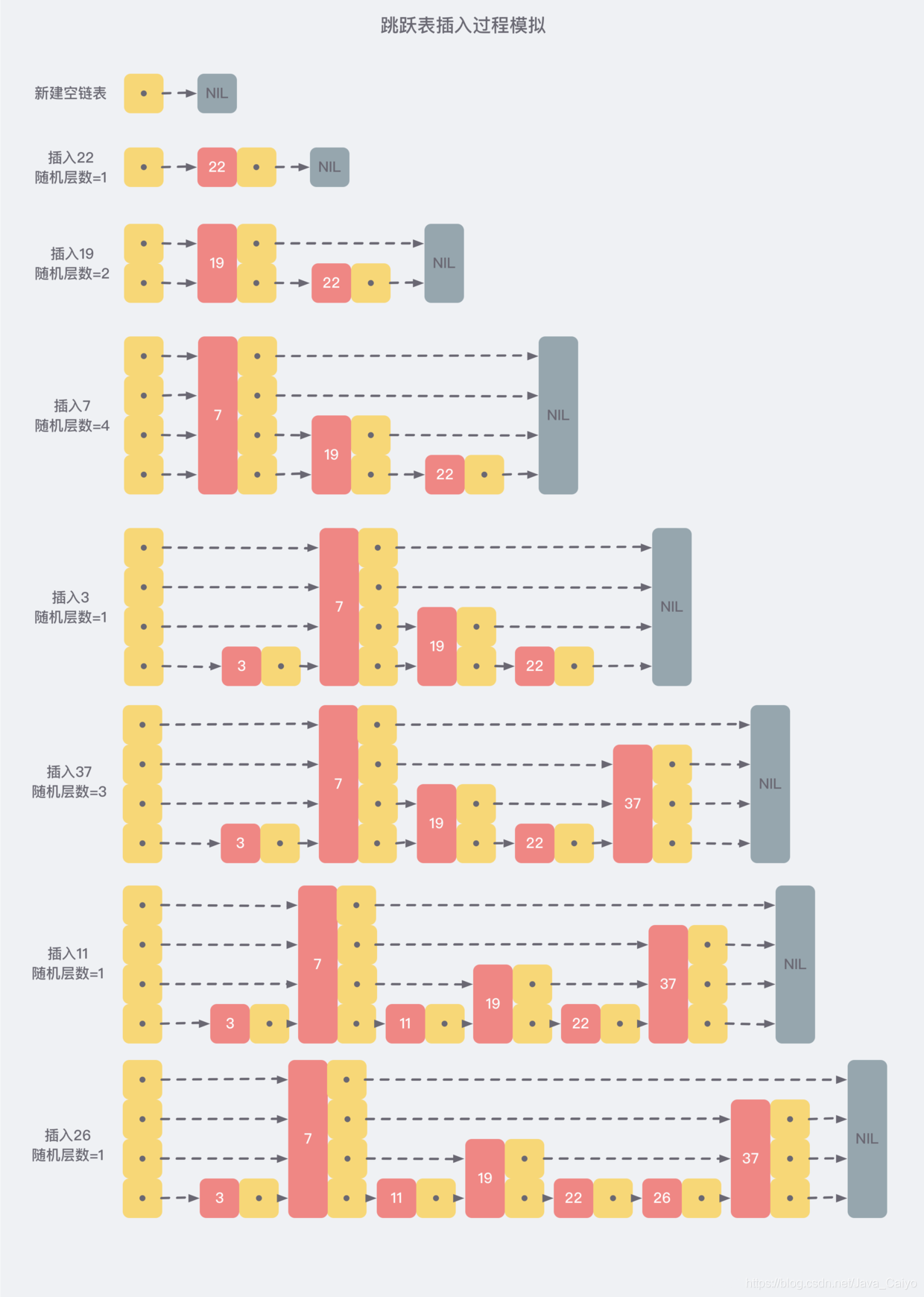
It can be seen from the above process of creation and insertion that the number of levels of each node is random, and the new insertion of a node will not affect the number of levels of other nodes. Therefore, the insertion operation only needs to modify the pointers before and after the node without adjusting multiple nodes, which reduces the complexity of the insertion operation.

Now let's assume that we find the nonexistent number 23 from the structure we just created, and the search path will be as follows:

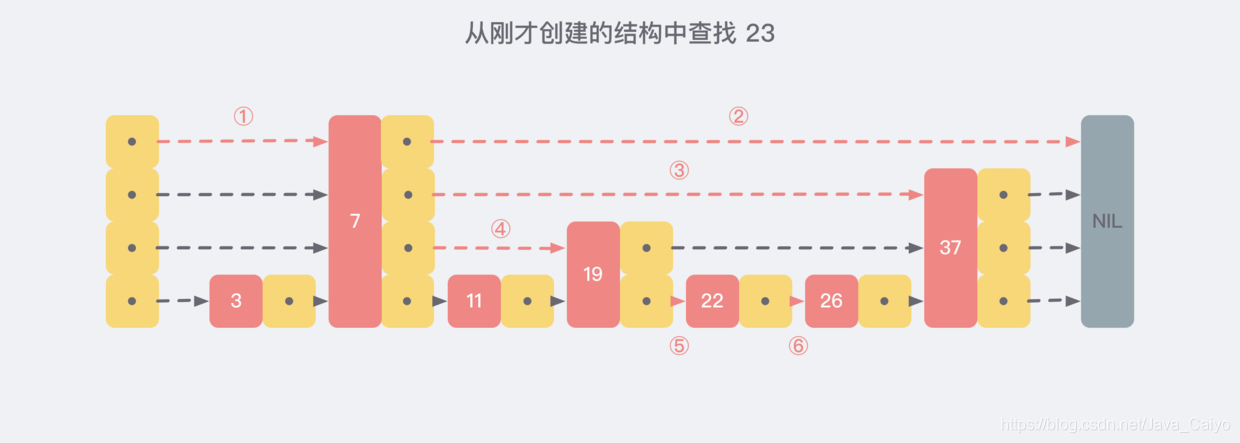
2. Implementation of jump table

The jump table in Redis is managed by server H / zskiplistNode and server H / zskiplist are two structure definitions. The former is a jump table node, and the latter saves the relevant information of the jump node. Similar to the previous set list structure, in fact, only zskiplistNode can be implemented, but the latter is introduced for more convenient operation:

/* ZSETs use a specialized version of Skiplists */ 
typedef struct zskiplistNode { 
	// value 
	sds ele; 
	// Score 
	double score; 
	// Back pointer 
	struct zskiplistNode *backward; 
	// layer 
	struct zskiplistLevel { 
		// Forward pointer 
		struct zskiplistNode *forward; 
		// span 
		unsigned long span; 
	} level[]; 
} zskiplistNode; 

typedef struct zskiplist { 
	// Skip header pointer 
	struct zskiplistNode *header, *tail; 
	// Number of nodes in the table 
	unsigned long length; 
	// The number of layers of the node with the largest number of layers in the table 
	int level; 
} zskiplist;

Just like the standard jump table drawn at the beginning of the article.

1) Random layers

For each newly inserted node, you need to call a random algorithm to assign it a reasonable number of layers. The source code is in t_ zset. Defined in C / zslrandomlevel (void):

int zslRandomLevel(void) { 
	int level = 1; 
	while ((random()&0xFFFF) < (ZSKIPLIST_P * 0xFFFF)) 
		level += 1; 
	return (level<ZSKIPLIST_MAXLEVEL) ? level : ZSKIPLIST_MAXLEVEL; 
}

Intuitively, the expected goal is that 50% probability is assigned to Level 1, 25% probability is assigned to Level 2, 12.5% probability is assigned to Level 3, and so on... 2-63 probability is assigned to the top layer, because the promotion rate of each layer here is 50%.

By default, the maximum number of layers allowed for Redis jump table is 32, which is zskiplist in the source code_ MAXLEVEL defines that only when Level[0] has 264 elements can it reach level 32, so the definition of 32 is completely sufficient.

2) Create jump table

This process is relatively simple. In the source code, t_ zset. Defined in C / zslcreate:

zskiplist *zslCreate(void) { 
	int j; 
	zskiplist *zsl; 
	
	// Request memory space 
	zsl = zmalloc(sizeof(*zsl)); 
	// The number of initialization layers is 1 
	zsl->level = 1; 
	// Initialization length is 0 
	zsl->length = 0; 
	// Create a skip header node with 32 levels, 0 score and no value 
	zsl->header = zslCreateNode(ZSKIPLIST_MAXLEVEL,0,NULL); 
	
	// Jump header node initialization 
	for (j = 0; j < ZSKIPLIST_MAXLEVEL; j++) { 
		// Set all forward pointers of the skip header node forward to NULL 
		zsl->header->level[j].forward = NULL; 
		// Set all span s of the skip header node to 0 
		zsl->header->level[j].span = 0; 
	}
	// The backward pointer of the jump header node is set to NULL 
	zsl->header->backward = NULL; 
	// The pointer from the header to the jump footer node is set to NULL 
	zsl->tail = NULL; 
	return zsl; 
}

That is, after execution, an initialization jump table with the following structure is created:

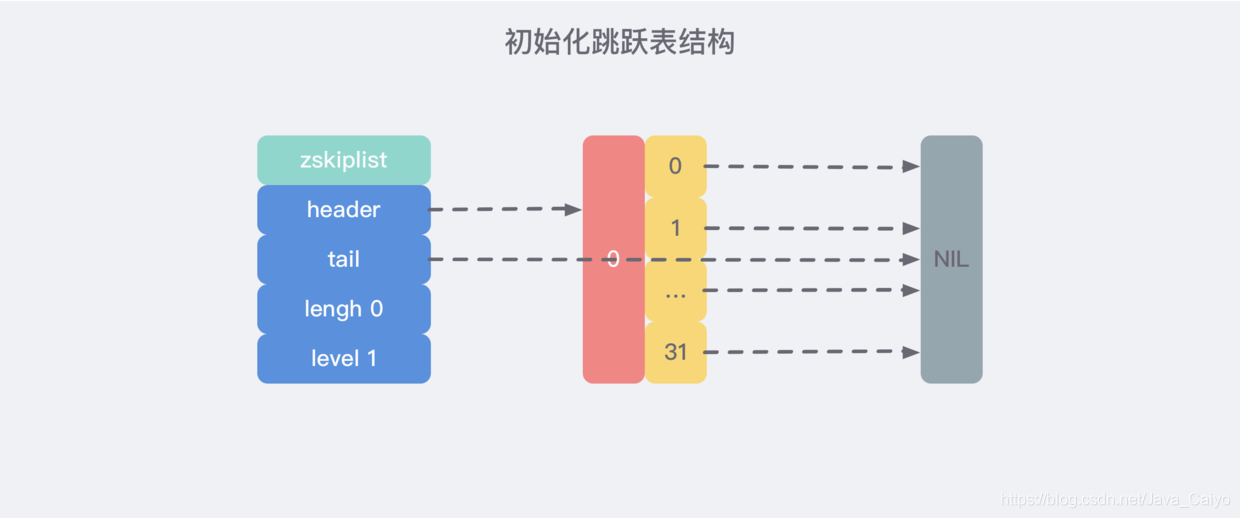
3) Insert node implementation

This is almost the most important piece of code, but the overall idea is also relatively clear and simple. If you understand the principle of the jump list mentioned above, it is easy to sort out several actions that occur when inserting nodes (almost similar to the linked list):

1. Find the current position I need to insert (including the processing when the score is the same);
2. Create a new node, adjust the pointer before and after to complete the insertion;

In order to facilitate reading, I put the source code t_ zset. The insertion function defined by C / zsinsert is divided into several parts

Part I: declare the variables to be stored

// Store search path 
zskiplistNode *update[ZSKIPLIST_MAXLEVEL], *x; 
// Storage node span 
unsigned int rank[ZSKIPLIST_MAXLEVEL]; 
int i, level;

Part 2: search the insertion position of the current node

serverAssert(!isnan(score)); 
x = zsl->header; 
// Step down to find the target node and get the "search path" 
for (i = zsl->level-1; i >= 0; i--) { 
	/* store rank that is crossed to reach the insert position */ 
	rank[i] = i == (zsl->level-1) ? 0 : rank[i+1]; 
	// If the score s are equal, you also need to compare the value value 
	while (x->level[i].forward && 
			(x->level[i].forward->score < score || 
				(x->level[i].forward->score == score && 
					sdscmp(x->level[i].forward->ele,ele) < 0))) 
	{ 
		rank[i] += x->level[i].span; 
		x = x->level[i].forward; 
	}
	// Record search path 
	update[i] = x; 
}

Discussion: in an extreme case, all score values in the jump table are the same. Will the lookup performance of zset degrade to O(n)?

From the above source code, we can find that the sorting element of zset not only looks at the score value, but also compares the value value (string comparison)

If the score s are equal, you also need to compare the value value
while (x->level[i].forward &&
(x->level[i].forward->score < score ||
(x->level[i].forward->score == score &&
sdscmp(x->level[i].forward->ele,ele) < 0)))
{
rank[i] += x->level[i].span;
x = x->level[i].forward;
}
//Record search path
update[i] = x;
}

Discussion: there is an extreme case, that is, all the items in the jump table score The values are the same, zset Will your discovery performance degrade to O(n) And?

From the above source code, we can find zset The sorting elements are not just looking score Values are also compared value Value (string comparison)