Binary sort tree
Binary sort tree properties:
- If its left subtree is not empty, the values of all nodes on the left subtree are less than the values of its root node
- If its left subtree is not empty, the values of all nodes on the left subtree are less than the values of its root node
- Its left and right subtrees are also binary sort trees
The order relationship between nodes: the left subtree node must be smaller than its parent node, and the right subtree node must be larger than its parent node
Purpose of binary sort tree:
Not to sort, but to improve the speed of finding, inserting and deleting keywords
Search the set {62,88,58,47,35,73,51,99,37,93}
62, 88 and 58 are created first
47
<
\lt
< 58, 47 is the left subtree, 35
<
\lt
< 47, 35 is the left subtree
73
>
\gt
>62 simultaneous 73
<
\lt
< 88, so 73 is the left subtree of 88
51
<
\lt
< 62 simultaneous 51
>
\gt
> 47
......

1. Binary list storage representation of binary sort tree
typedef struct{
KeyType key; //Keywords to find
InfoType otherinfo; //Other data items
}ElemType; //Type of data field of each node
typedef struct BSTNode{
ElemType data; //The data field of each node includes keywords and other data items
struct BSTNode *lchild,*rchild; //Left and right child pointers of nodes
}BSTNode,*BSTree;
2. Search binary sort tree
BSTree SearchBST(BSTree T, KeyType key){
if((!T) || key == T->data.key)
return T;
else if(key < T->data.key)
return SearchBST(T->lchild,key);
else
return SearchBST(T->rchild,key);
}
Hypothetical lookup 93
T currently points to node 62, key=93, T - > data key=62,key
>
\gt
> T->data.key
Recursion, T - > rchild points to node 88, key=93, T - > data key=88,key
>
\gt
> T->data.key
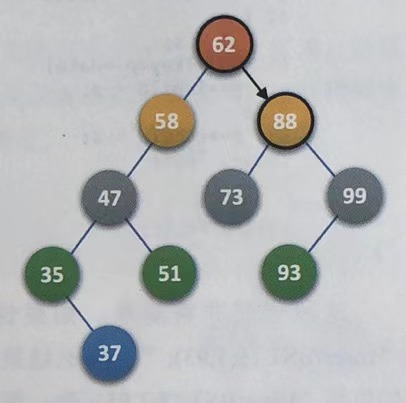
Recursion, T - > rchild points to node 99, key=93, T - > data key=99,key
<
\lt
< T->data.key
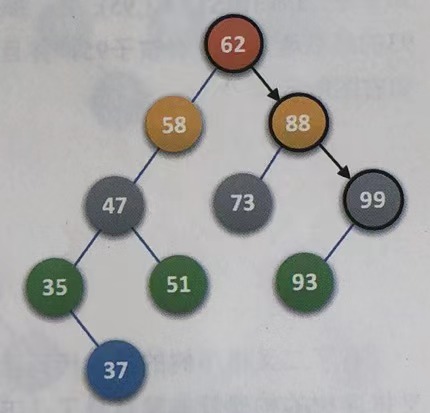
Recursion, T - > lchild points to node 93, key = 93, T - > data key=93,key
=
=
= T->data.key
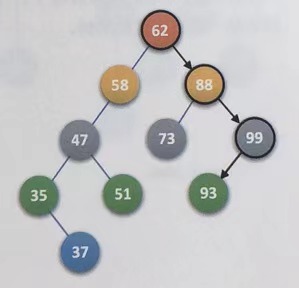
3. Insertion of binary sort tree
void InsertBST(BSTree &T, ElemType e){
if(!T){ //The tree is not empty
S=new BSTNode; //New node S
S->data=e; //The data field of S is set to e
S->lchild=S->rchild=NULL; //Initialization of left and right children of S
T=S; //Link node S to the found insertion location
}
else if(e.key < T->data.key)
InsertBST(T->lchild, e);
else
InsertBST(T->rchild, e);
}
Suppose 95 is inserted
T currently points to node 62,! T=0
e.key=95,T->data.key=62,e.key
>
\gt
> T->data. Key, recursive, T - > rchild, pointing to 88
T currently points to node 88,! T=0
e.key=95,T->data.key=88,e.key
>
\gt
> T->data. Key, recursive, T - > rchild, pointing to 99
T currently points to node 99,! T=0
e.key=95,T->data.key=99,e.key
<
\lt
< T->data. Key, recursive, T - > lchild = null
!T=1
Create node S, set its data field to e, leave the left and right children blank, and link S to the position indicated by the current T
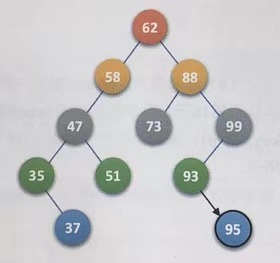
4. Delete binary sort tree
There are three ways to delete a node:
1. Delete leaf node
f->lchild=NULL //f refers to the parent of the node to be deleted perhaps f->rchild=NULL
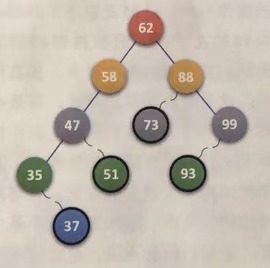
2. The node to be deleted has only left subtree / left child or only right subtree / right child
//f points to the parent of the node to be deleted, and p points to the node to be deleted f->lchild=p->lchild; //F - > lchild points to the node indicated by P - > lchild perhaps f->lchild=p->rchild; //F - > lchild points to the node indicated by P - > rchild
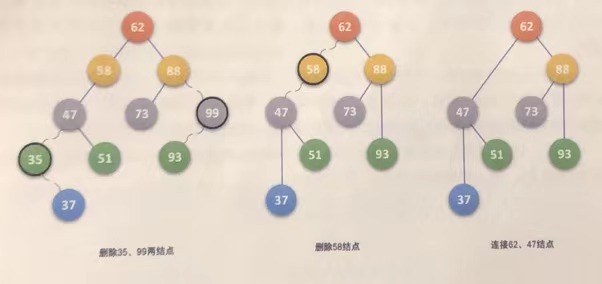
3. The left and right subtrees of the node to be deleted are not empty
Node algorithm description of deleting keyword key in binary sort tree
The pointer p points to the deleted node
The pointer f points to the parents of the deleted node
void DeleteBST(BSTree &T, KeyType key){
p=T; //Initialize pointer p
f=NULL; //Initialize pointer f
//The while loop starts from the root (the top vertex of the tree, which is different from the root node) to find the node * p of the keyword key
while(p)
{
if(p->data.key == key) //Node p data field is equal to keyword, search succeeded
break;
f=p; //f points to the node indicated by p
if(p->data.key > key) //Node p data field is larger than keyword
p=p->lchild; //Update p points to its left child
else node p Data field is smaller than keyword
p=p->rchild; //Update p points to its right child
} //while end
if(!p) //Deleted node not found
return;
//The left and right subtrees of the deleted node are not empty
q=p; //q points to the node indicated by p
if((p->lchild) && (p->rchild)) //The left and right children of node p are not empty
{
s=p->lchild; //s points to the node indicated by P - > lchild
while(s->rchild) //Find the rightmost lower node of p left subtree
{
q=s; //q points to the node referred to by s
s=s->rchild; //Update s to point to the node indicated by S - > rchild
} //while end
p->data=s->data; //The data field of node s is assigned to the data field of node p (overwrite operation)
if(q != p) //q and p refer to different nodes
q->rchild=s->lchild; //Q - > rchild points to the node indicated by S - > lchild
else //q and p refer to the same node
q->lchild=s->lchild; //Q - > lchild points to the node indicated by S - > lchild
delete s; //Delete node s
return;
}
else if(!p->rchild) //The right child of node p is empty
p=p->lchild;
else if(!p->lchild) //The left child of node p is empty
p=p->rchild;
//Hang the subtree indicated by p to the corresponding position of its parent node * f
if(!f) //The deleted node is the root node (the top node of the subtree)
T=p;
else if(q==f->lchild)
f->lchild=p; //Left subtree position attached to f
else
f->rchild=p; //Hanging to the right subtree of f
delete q; //Delete node q
}
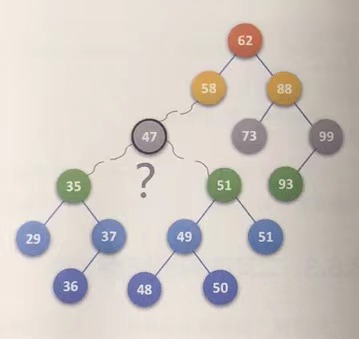
Suppose node 47 is deleted
q=p;
if((p->lchild) && (p->rchild))
{
s=p->lchild; //Initialize pointer s
...
}
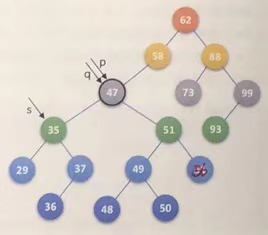
...
if((p->lchild) && (p->rchild))
{
...
while(s->rchild) //Find the rightmost lower node of the left subtree of p, and find node 37 here
{
q=s; //q goes from pointing node 47 to pointing node 35
s=s->rchild; //s goes from pointing node 35 to pointing node 37
} //while end
...
}
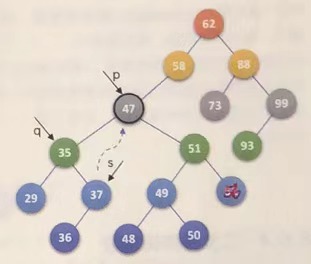
...
if((p->lchild) && (p->rchild))
{
...
while(s->rchild) //Find the rightmost lower node of the left subtree of p, and find node 37 here
{
q=s; //q goes from pointing node 47 to pointing node 35
s=s->rchild; //s goes from pointing node 35 to pointing node 37
} //while end
p->data=s->data; //Overlay node 37 over node 47
}
Why should node 37 override node 47?
Among the left and right subtrees of 47, 37 and 48 are the two closest to 47. Select one of these two trees to cover 47.
The rightmost node on the left subtree of the deleted node overwrites the deleted node
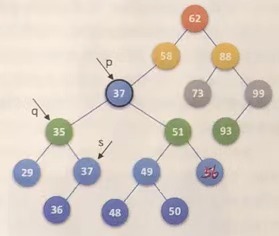
...
if((p->lchild) && (p->rchild))
{
...
while(s->rchild) //Find the rightmost lower node of the left subtree of p, and find node 37 here
{
q=s; //q goes from pointing node 47 to pointing node 35
s=s->rchild; //s goes from pointing node 35 to pointing node 37
} //while end
p->data=s->data; //Overlay node 37 over node 47
if(q != p) //q and p refer to different nodes
q->rchild=s->lchild; //Q - > rchild points to the node indicated by S - > lchild
... //Link node 36 to node 35
...
}
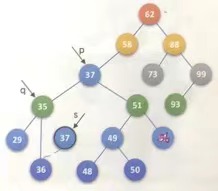
...
if((p->lchild) && (p->rchild))
{
...
while(s->rchild) //Find the rightmost lower node of the left subtree of p, and find node 37 here
{
q=s; //q from point 47 to point node 35
s=s->rchild; //s goes from pointing node 35 to pointing node 37
} //while end
p->data=s->data; //Overlay node 37 over node 47
if(q != p) //q and p refer to different nodes
q->rchild=s->lchild; //Link node 36 to node 35
else //q and p refer to the same node
q->lchild=s->lchild; //Q - > lchild points to the node indicated by S - > lchild
delete s; //Delete node s
return;
}
