7-1, then what time (15 minutes)
Sometimes people use four digits to represent a time. For example, 1106 means 11:06. Now, your program calculates the end time based on the start time and the elapsed time.
Read in two numbers. The first number represents the current time with such four digits, and the second number represents the minutes. Calculate the time after so many minutes, and the result is also expressed as four digits. When the hour is a single digit, there is no leading zero, for example, 5:30 is represented as 530; 0:30 means 0:030. Note that the second number may represent more than 60 minutes or a negative number.
Input format:
Input gives 2 integers in one line, which are the starting time represented by four digits and the elapsed minutes, separated by spaces. Note: in the start time, when the hour is a single digit, there is no leading zero, that is, 5:30 is 530; 0:30 means 0:030. The number of minutes passed may be more than 60 or negative.
Output format:
Output the termination time represented by no more than four digits. When the hour is a single digit, there is no leading zero. The title ensures that the start time and end time are within the same day.
Input example:
1120 110
No blank lines at the end
Output example:
1310
No blank lines at the end
Thanks to teacher Mu Yunfeng and user Ren Yu of Yanshan University for supplementary data!
#include<stdio.h>
int main()
{
//Storage start time, minutes elapsed
int a,b;
//Reception start time and elapsed minutes
scanf("%d %d",&a,&b);
//Store the hours and minutes of the start time respectively
int h=0,m=0;
//Calculate hours
//For example, a=1523, h=15 after calculation
h=a/100;
//Calculate minutes
m=a-h*100;
//Calculate and store hours and minutes of elapsed time
int ym=b%60,yh=b/60;
//Minutes of start time plus minutes of elapsed time
m+=ym;
//If M > 60, add one to the number of hours and change the number of minutes into a legal number of minutes
if(m>=60)
{
yh++;
m-=60;
}
//If M < 60, the hours are subtracted by one and the minutes become legal minutes
else if(m<0)
{
yh--;
m+=60;
}
//The hours of the start time plus the hours of the elapsed time
h+=yh;
//The stem of the question indicates that the start time and end time are the same day. This judgment does not need to be added
/*if(h>=24)
h-=24;*/
//When printing, you do not need to add the leading 0 to the hours, but add the leading 0 to the minutes,
printf("%d%02d\n",h,m);
return 0;
}7-2 calculation index (10 points)
I really didn't lie to you. This is a simple problem - for any given positive integer , n not exceeding 10, you are required to output , 2n. Isn't it hard?
Input format:
The input gives a positive integer n of no more than 10 in one line.
Output format:
Output 2n value in one row according to format 2^n = calculation result.
Input example:
5
No blank lines at the end
Output example:
2^5 = 32
No blank lines at the end
#include<stdio.h>
#include<math.h>
int main()
{
//Receive and store power
int a;
scanf("%d",&a);
//Store the a-th power of 2
int b=pow(2,a);
//Print
printf("2^%d = %d",a,b);
return 0;
}7-3 find the spherical distance between two points on the equator (10 points)
It is known that the equatorial radius of the earth is 6378.137 km, We also know the longitude (in degrees) of two points on the equator in the eastern hemisphere, and write a program to calculate the spherical distance between these two points. All real numbers are required to use double type, and the approximate value of PI is 3.141592653589793. Note: the spherical distance between two points on the equator is the length of the inferior arc between two points on the equator.
Input format:
Enter two non negative real numbers representing longitude on one line, separated by spaces.
Output format:
Output the value of spherical distance, keep 3 decimal places, and finally wrap.
Input example:
63.2 136.9
No blank lines at the end
Output example:
8204.246
No blank lines at the end
#include<stdio.h>
#include<math.h>
int main()
{
//Receive and store longitude
double a,b;
scanf("%lf %lf",&a,&b);
//Stores the absolute value of the difference between two longitudes
double c=fabs(a-b);
//Storage radius and PI
double r=6378.137,p=3.141592653589793;
//Store the arc length, that is, the distance between two points on the equator
double d=r*(p*c/180);
//Print
printf("%.3lf\n",d);
return 0;
}7-4 integer arithmetic operation (10 points)
This problem requires writing a program to calculate and output the sum, difference, product, quotient and remainder of two positive integers. The problem is to ensure that the input and output are all within the integer range.
Input format:
Input gives two positive integers A and B in one line.
Output format:
Output the sum, difference, product, quotient and remainder in the order of "A operator B = result" in 5 lines.
Input example:
5 3
No blank lines at the end
Output example:
The corresponding output is given here. For example:
5 + 3 = 8 5 - 3 = 2 5 * 3 = 15 5 / 3 = 1 5 % 3 = 2
No blank lines at the end
#include<stdio.h>
int main()
{
//Receive and store two numbers
int a,b;
scanf("%d %d",&a,&b);
//Print
printf("%d + %d = %d\n",a,b,a+b);
printf("%d - %d = %d\n",a,b,a-b);
printf("%d * %d = %d\n",a,b,a*b);
printf("%d / %d = %d\n",a,b,a/b);
//Add one more percent sign to make the percent sign output
printf("%d %% %d = %d\n",a,b,a%b);
return 0;
}7-5 calculation of shaded area based on inclusion exclusion principle (10 points)
The inclusion exclusion principle is an important combinatorial method, which allows you to solve sets of any size or calculate the probability of composite events. It can be described as calculating the size of the union of several sets. We should first calculate the size of all single sets, then subtract the intersecting parts of all two sets, add back the intersecting parts of all three sets, and then subtract the intersecting parts of all four sets. According to this deduction, we can calculate the intersecting parts of all sets.
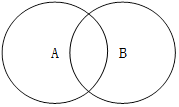
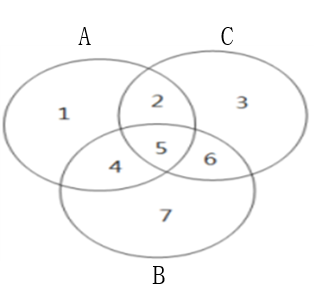
As shown in the above figure, if the sets A and B are known, then | A ∪ B| = |A| + |B |- |A ∩ B |; If the set A,B,C is known, then | A ∪ B ∪ C | = | A | + | B | + | C | - A ∩ B| - |B ∩ C| - |C ∩ A| + |A ∩ B ∩ C |. It is now known that the rectangular ABCD takes AB as the radius as the extension line of fan-shaped intersection AD at f and CB as the radius as the fan-shaped intersection CD at F, as shown in the figure below. The length and width of the known rectangle are x and Y respectively to calculate the area of the shaded part.
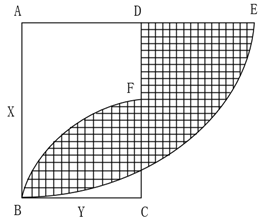
Note: 1 Area formula of sector: S = n π r ^ 2 / 360 = LR / 2 (where n is the degree of sector center angle, r is sector radius, L is arc length, π = 3.1415926) 2 Area formula of rectangle: S = AB (where a and B are length and width respectively)
Input format:
The input gives two positive real numbers X and y not exceeding 100 in one line, and ensures that X > = Y > = 1.
Output format:
Output the area of the shaded part in one line, and keep the result to two decimal places.
Input example:
A set of inputs is given here. For example:
6 5
No blank lines at the end
Output example:
The corresponding output is given here. For example:
17.91
No blank lines at the end
#include<stdio.h>
int main()
{
//Store and receive length and width
double a,b;
scanf("%lf %lf",&a,&b);
//Stored pi
double p=3.1415926;
/*
In fact, this problem doesn't need to look at the collection in the problem
In fact, I won't. I regard this problem as a simple problem of finding area
In fact, the area is the large quarter circle area minus the blank area on the rectangle
The blank area above the rectangle is the area of the rectangle minus the area of the smaller quarter circle below
So the answer to this question came out
*/
//Store rectangular area
double sc=a*b;
//Store large quarter circle area
double sd=p*a*a/4;
//Store small quarter circle area
double sx=p*b*b/4;
//Stores the empty area above the rectangle
double ss=sc-sx;
//Storage shadow area
double sq=sd-ss;
//Print
printf("%.2lf\n",sq);
return 0;
}Generally speaking, today's topic has understood the meaning. It's very simple, but please repeat it!!!