Bubble sorting

Step analysis and introduction

1. As can be seen from the figure below, when comparing two adjacent elements, the large number will move backward (how to move it later?), so after each comparison, a larger number will be placed at the end, and the last number does not need to be compared, that is, after each comparison, the comparison times of two adjacent elements will be relatively reduced (how much is the relative reduction?).
2. Next, we analyze how to move large numbers backward. At this time, we need an intermediate variable temp. If a[i] > a[i+1], we can assign a[i] to temp, then assign a[i+1] to a[i], and then assign a[i] in temp to a[i+1]. This is to achieve large backward movement.
3. The number of rounds and times of comparison are analyzed and compared, as shown in the figure below. There are nine rounds in total, and we need to compare 8 rounds.
   The first round - 8 comparisons in pairs
   The second round - 7 comparisons in pairs
   The third round - 6 comparisons in pairs
   The fourth round ------ 5 times of pairwise comparison
   ...
   The seventh round - two comparisons twice
   The eighth round - one comparison in pairs

The picture presentation process is as follows

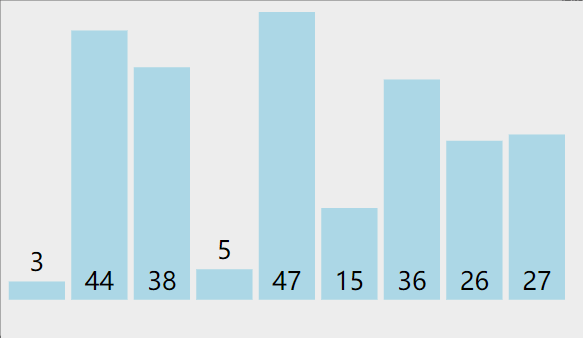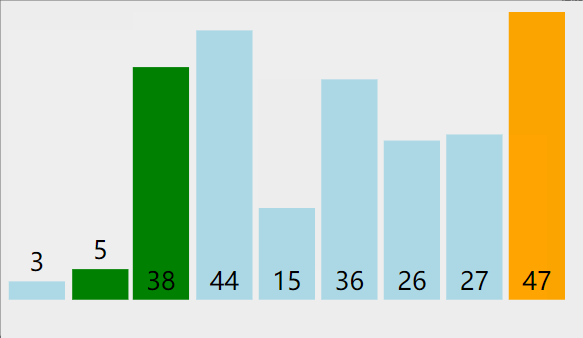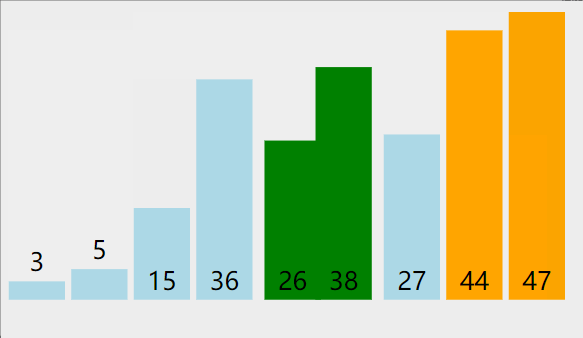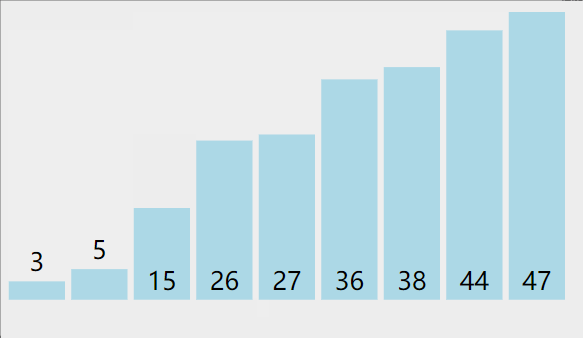
code implementation

public class PaiXuDemo {
    public static void main(String[] args) {
    	//Keyboard input
        Scanner scanner = new Scanner(System.in);
        //Define an array with an array length of 5
        int[] arr = new int[8];
        System.out.println("Please enter 5 numbers");
        //Use the for loop to implement the digital input of the array
        for (int i=0;i<arr.length;i++){
            arr[i]=scanner.nextInt();
        }
        
     	//i represents the number of rounds compared, and arr.length-1 represents the length of the array minus one
		for (int i=0;i<arr.length-1;i++){
		//j represents the number of comparisons between two
		            for (int j=0;j<arr.length-i-1;j++){
		            //Realize the backward movement of large numbers
		                if (arr[j]>arr[j+1]){
		                    int temp = arr[j];
		                    arr[j]=arr[j+1];
		                    arr[j+1]=temp;
		                }
		            }
		        }
		//Use the for loop to iterate through each number in the output array
        for (int n=0;n<arr.length;n++){
            System.out.print(arr[n]+" ");
        }
}

Select sort

Step analysis and introduction

1. As shown in the following figure: we can see that it starts with the number in the first position that is not sorted, and then compares it one by one from the second number. When it is found that the number in front is larger than the number in a certain position in the back, exchange the position of the number in front with the number in the back (how to exchange this?), and then continue to compare back. The numbers in front of the comparison will get ordered numbers. After multiple rounds and multiple comparisons, we will get ordered array elements (how many times and how many times do we need to compare).
2. Next, we analyze how to exchange the position between the front number and the rear number. At this time, we need an intermediate variable temp. If a[i] > a[j], we can assign a[i] to temp, then assign a[j] to a[i], and then assign a[i] in temp to a[j]. This is to realize the exchange position between the front number and the rear number
3. The number of rounds and times of comparison are analyzed and compared, as shown in the figure below. There are 7 rounds in total, and we need to compare 6 rounds
The first round - 6 comparisons
The second round - comparison 5 times
The third round - 4 Comparisons
...
Round 6 - comparison 1 time

The picture presentation process is as follows

code implementation

//The definition of array and keyboard input array elements are consistent with bubble sorting. I won't write it here, ha ha ha!!! Directly focus on the code!!!!!!!!!!!

// k controls the number of rounds. Here, starting from the first number, the number of rounds compared, that is, the length of the array, is reduced by one
  for (int k=0;k<arr.length-1;k++){
  //l control the times of each round of comparison, that is, start with the second number of the previous number, and the previous number is compared with each subsequent number
            for (int l=k+1;l<arr.length;l++){
            //Realize the position exchange between the previous number and the subsequent number
                if (arr[k]>arr[l]){
                    int temp = arr[k];
                    arr[k] = arr[l];
                    arr[l] = temp;
                }
            }
        }

Insert sort

Step analysis and introduction

1. Start with the first element, which can be considered to have been sorted, then take out the next element and scan from back to front in the sorted element sequence. If the latter element is compared with the previous element, if the latter element is smaller than the former element, insert the latter element in front of the former element, that is, move the former element back one position, Insert the following elements, and then continue to compare them forward until they are no smaller than the previous elements
2. As shown in the figure below, a total of 7 rounds are compared

The picture presentation process is as follows

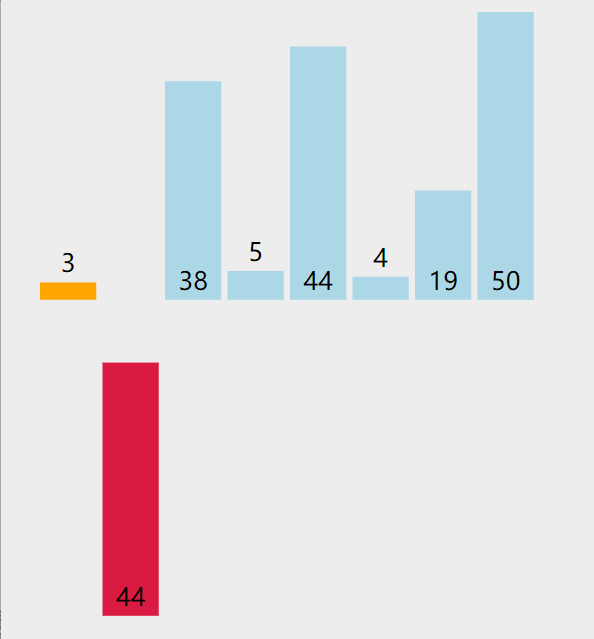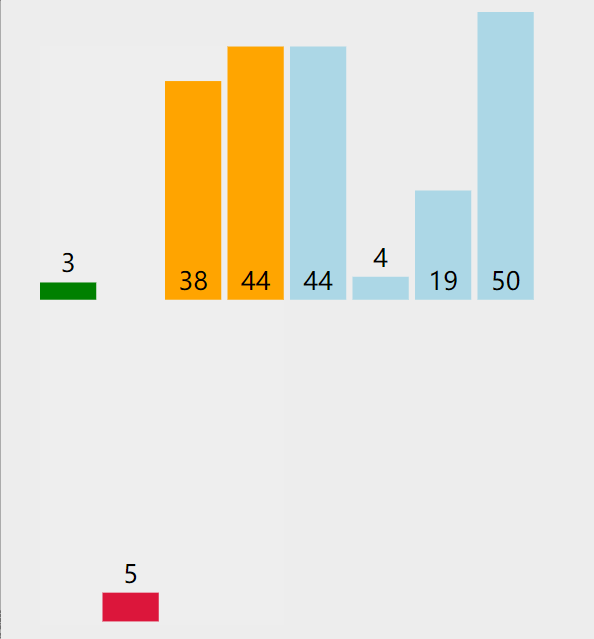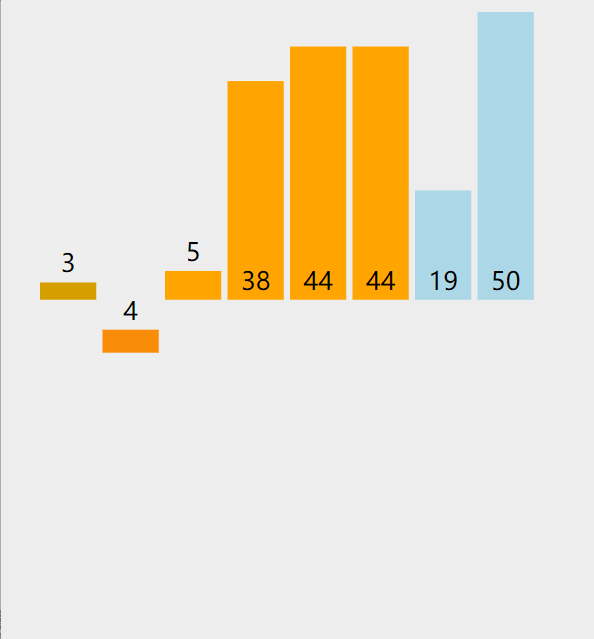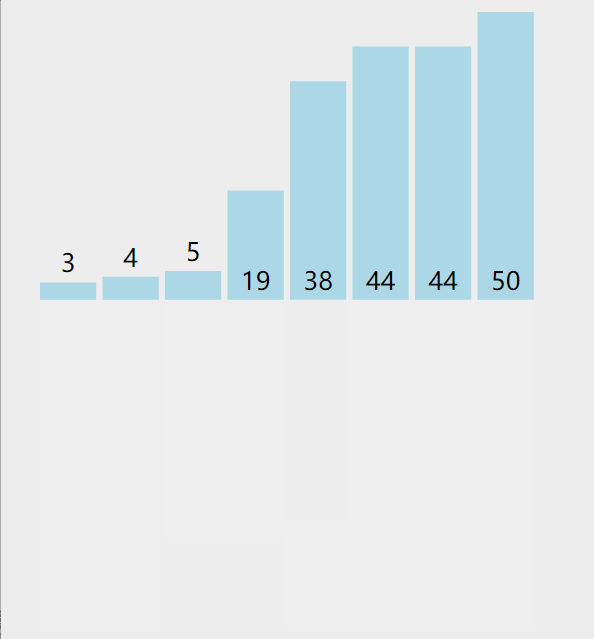
code implementation

//The definition of array and keyboard input array elements are consistent with bubble sorting. I won't write it here, ha ha ha!!! Directly focus on the code!!!!!!!!!!!

//Controls the number of rounds compared
	 for (int n=1;n<arr.length;n++){
            int temp = arr[n];
            //Number of comparisons
            for (int m=n;m>0;m--){
            //Judge whether the following number is larger than the previous one
                if (temp < arr[m-1]){
                //Move the front number back to make room for the small number to insert
                    arr[m]=arr[m-1];
                    arr[m-1] = temp;
                }
            }
        }

Summary

Personal understanding, boss, give more advice!!!