1. Preface

HashMap is definitely the essence of JDK source code. In addition, there are AQS, thread pool and so on. However, because HashMap is the earliest and most contacted by us, its existence is absolutely indispensable in the interview eight part essay.

If you want to learn a technology, you can probably understand its principle. In fact, it's almost the same, but interviewers often ask you the bottom, such as put process, resize process, why the load factor is 0.75 and so on

In fact, these are all good. The most troublesome thing is the hash algorithm. Let's take a look at jdk1 Source code for calculating subscript in 8:

static final int hash(Object key) {
    int h;
    return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}

In addition, there is another sentence. This hash is the value obtained above, and n is the array length:

(n - 1) & hash

So here comes the question...:

• Why shift 16 bits to the right?
• Why do you want to XOR (^) with yourself?
• Why n-1?
• Why is it bit operation rather than modulo?

With these questions, let's read on.

2. Target of hash algorithm

We all know the principle of HashMap. Hash a key to get the subscript, and then store the value corresponding to the key in the array.

Let's assume that the array capacity is 16. What if a hashcode value of 9999 comes at this time? Using 9999 as a subscript directly will cross the boundary, so we need to do further processing:

Ensure that the result of hash operation is within the capacity range.

2.1 how to ensure efficiency?

Some people say it's not easy. Won't it be finished by taking the mold directly?

hashcode % 16

All right, we're done with our hash algorithm. If this is written in your business code, of course there is no problem. But this is the JDK source code, the cornerstone of your business code operation, and the essence of modular operation:

1. Find integer quotient: c = a/b;
2. Calculation modulus / remainder: r = a - (c*b);

It can be seen that this includes division, multiplication and subtraction. The efficiency of direct modulus is too low. Is there any method to replace modulus?

Of course:

When length is to the nth power of 2, the calculated value of (length-1) & hashcode is consistent with hashCode%length

So our algorithm has been improved:

(length-1)&hashCode

Eh? Isn't this the (n - 1) & hash in the JDK source code? In addition, we have an unexpected gain: why is the capacity of HashMap N-power of 2.

2.2 how to reduce hash conflicts?

Efficiency is raised, and new problems come again:

String a = "Zhang San";
String b = "Li Si";
String c = "Wang Wu";
String d = "Zhao Liu";
int length = 31;
System.out.println(a.hashCode() & length);
System.out.println(b.hashCode() & length);
System.out.println(c.hashCode() & length);
System.out.println(d.hashCode() & length);

Suppose we have two hashcode values a and b. using the algorithm we just deduced, the calculated subscript is as follows:

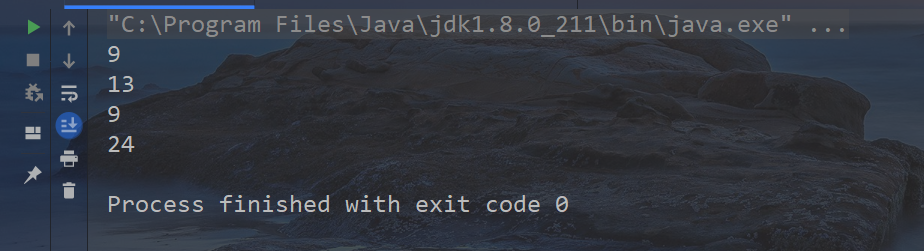
It can be seen that there is a conflict between the subscripts of Zhang San and Wang Wu. What about the seemingly less intelligent sub son of this algorithm?

This is also simple. We can perturb the hash algorithm.

2.3 how to disturb?

In fact, when length=8, the subscript operation result depends on the lower three bits of the hash value; when length=16, the subscript operation result depends on the lower four bits of the hash value, and so on. We come to the conclusion:

When length=2 to the nth power, the result of the subscript operation depends on the lower N bits of the hash value.

In other words, when we perform (n - 1) & hash, we actually take the value of the lower N bits, so how to make the value of the lower N bits more evenly distributed?

Use a fixed value to calculate again? This is too rigid. What we need is more random and more uniform. So can we let it do something to itself?

Let it be XOR with the upper 16 bits! After moving the upper 16 bits unsigned to the right, XOR is performed with the lower 16 bits. The features of the upper 16 bits and the features of the lower 16 bits can be mixed, and the high-order and low-order information in the new value is retained.

The reason why XOR operation is adopted here instead of &, | operation is that XOR operation can better retain the characteristics of each part. If & operation is adopted, the value calculated will be close to 1, and the value calculated by | operation will be close to 0.

So our algorithm has been improved again:

(hashCode ^ (hashCode >>> 16)) & (length-1)

Isn't this the practice in the JDK source code?

2.4 what is the effect of the new algorithm?

Let's run it again with the algorithm just deduced:

String a = "Zhang San";
String b = "Li Si";
String c = "Wang Wu";
String d = "Zhao Liu";
int length = 31;
System.out.println(a.hashCode() & length);
System.out.println(b.hashCode() & length);
System.out.println(c.hashCode() & length);
System.out.println(d.hashCode() & length);
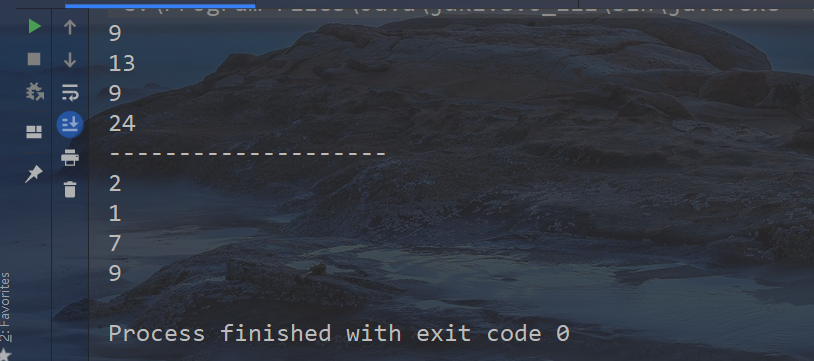
System.out.println("--------------------");
System.out.println((a.hashCode() ^ a.hashCode() >>> 16) & length);
System.out.println((b.hashCode() ^ b.hashCode() >>> 16) & length);
System.out.println((c.hashCode() ^ c.hashCode() >>> 16) & length);
System.out.println((d.hashCode() ^ d.hashCode() >>> 16) & length);

The result is obvious. The calculated subscripts are obviously much more uniform!

3. Conclusion

We should all know the problems raised here. In fact, there are some extended problems in this paper, such as: how does the computer carry out multiplication and division? Why can bit operations replace modulo? Do you have to shift the upper 16 bits to the right? How about eight and twelve?

These questions are left for readers to think about. If you have any questions, please leave a message in the comment area!