JavaScript data structure and algorithm (Part 2)
In the last article, we learned a lot of data structures, including stack, queue, dictionary, linked list and so on. I hope you can absorb them one by one and we will make progress together. In this article, we will explore the mysteries of trees and graphs, and I will introduce several algorithms to arm our algorithm system. Start learning!
7, Tree
(1) Common tree
- Concept: what is a tree? A tree is a data structure similar to a tree in our life, which is composed of nodes and edges. Many scenes in our life can be described by trees, such as the company's position structure, family relationship spectrum, food chain, etc. Therefore, it is very important for us to study the characteristics of trees and learn trees.
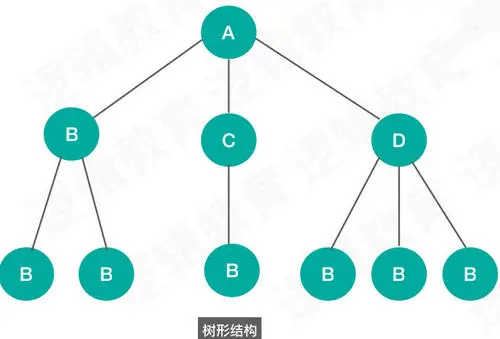
- The above figure can well represent the structure of A tree. We need to understand several concepts. For example, A is the root node of the tree. Because A has three child nodes, A can also be called A 3-degree node. Then you can silently tell me how many degree nodes D, C and B are? And there are many B's at the bottom. All B's are essentially leaf nodes!
- This is a common tree, which is composed of several points and edges. Each node has its own value and also stores references to other nodes.
(2) Binary tree
- What is a binary tree? In fact, a binary tree is a tree in which each node is at most a second-degree node, that is, as long as the number of its child nodes does not exceed two nodes, such a tree can be called a binary tree, and any tree can be regarded or converted into a binary tree through certain operations.
- Compared with ordinary trees, binary trees have some specific laws, so the study of binary trees is actually a very important topic!
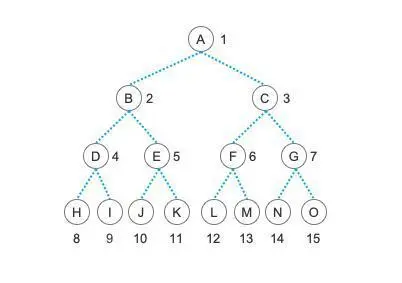
- The above is a standard binary tree and a perfect binary tree. You can see that each node has no more than two nodes. In this case, we can also classify. Some binary trees with incomplete symmetrical branches are called complete binary trees, and the rest are called ordinary binary trees
(3) Binary search tree
- Now we want to know an important topic, binary search tree
- What is a binary search tree
- In accordance with the principle of binary tree, we can meet the following requirements
1. If its left subtree is not empty, the values of all nodes on the left subtree are less than the values of the root node
2. If its right subtree is not empty, the values of all nodes on the right subtree are greater than those of the root node
3. Its left and right subtrees are also binary search trees
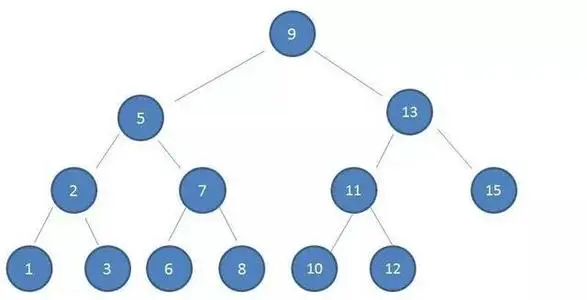
- Look at the above example. The numbers of all nodes on the left side of the root node are smaller than the root node, and the numbers on the right side are larger than the root node. And fully meet the requirements of the above three points, so we can confidently call the tree above as a binary search tree.
- But the question is, what's his use!
- A: its search efficiency is very high. We will package it later.
- You can find that the binary tree is orderly. Therefore, when we want to find a data, we don't have to compare and traverse one by one. First, we compare it with the root node. If it is larger than the root node, the target must be on the right, otherwise, it must be on the left. In this way, half of the data is excluded, so the search efficiency is greatly improved.
- And the more average a binary search tree is, the fewer levels are, and the higher the search efficiency is. Therefore, when creating a binary search tree, we should also distribute the binary search tree as evenly as possible! This is also an important topic.
- Well, having said so much, let's formally encapsulate the binary search tree!
// Encapsulation node
class TreeNode {
constructor(data, left, right) {
this.data = data
this.left = null
this.right = null
if (left && left < data) {
this.left = left
}
if (right && right > data) {
this.right = right
}
}
}
//Encapsulated binary search tree
class BinarySearchTree {
constructor(root) {
this.root = root || null
this.size = 0
}
whitchIn(node, newNode) {
if (newNode.data > node.data) {
// The description is larger and should be inserted on the right
if (node.right === null) {
node.right = newNode
} else {
this.whitchIn(node.right, newNode)
}
} else {
if (node.left === null) {
node.left = newNode
} else {
this.whitchIn(node.left, newNode)
}
}
}
insert(data) {
if (this.root == null) {
const newNode = new TreeNode(data)
this.root = newNode
} else {
// Call recursive function
const newNode = new TreeNode(data)
this.whitchIn(this.root, newNode)
}
this.size++
return this
}
// Depth first traversal
foreach(handler, type = 'first') {
this.forFun(this.root, handler, type)
}
forFun(node, handler, type) {
if (node !== null) {
if (type === 'first') {
handler(node.data)
}
this.forFun(node.left, handler, type)
if (type === 'middle') {
handler(node.data)
}
this.forFun(node.right, handler, type)
if (type === 'last') {
handler(node.data)
}
}
}
min(current = this.root, returnType = 'data') {
while (current.left !== null) {
current = current.left
}
if (returnType === 'data') {
return current.data
} else {
return current
}
}
max(current = this.root, returnType = 'data') {
let parentNode = null
while (current.right !== null) {
parentNode = current
current = current.right
}
if (returnType === 'data') {
return current.data
} else {
return [current, parentNode]
}
}
search(data) {
let node = this.root
while (node !== null) {
if (data > node.data) {
node = node.right
} else if (data < node.data) {
node = node.left
} else {
return true
}
}
return false
}
remove(data) {
let parentNode = null
let isLeft = true
let current = this.root
while (current != null) {
if (data > current.data) {
isLeft = false
parentNode = current
current = current.right
} else if (data < current.data) {
isLeft = true
parentNode = current
current = current.left
}
}
if (current.left === null && current.right === null) {
if (current === this.root) {
this.root = null
} else {
if (isLeft) {
parentNode.left = null
} else {
parentNode.right = null
}
}
} else if (current.left === null) {
if (isLeft) {
parentNode.left = current.right
} else {
parentNode.right = current.right
}
} else if (current.right = null) {
if (isLeft) {
parentNode.left = current.left
} else {
parentNode.right = current.left
}
} else {
// This is the famous third case, where neither side is zero
let [current = replaceNode, parentNode = replaceParentNode] = this.max(current.left, 'node')
let replaceLeft = replaceNode.left
if (replaceNode.left !== null) {
replaceParentNode.right = replaceLeft
}
replaceNode.left = current.left
replaceNode.right = current.right
if (isLeft) {
parentNode.left = replaceNode
} else {
parentNode.right = replaceNode
}
}
}
}
-
In fact, most of them are easy to understand in the packaging process, but the deletion operation is still troublesome. There are many situations to consider. Let me sort out my ideas!
-
First, we will get a point to be deleted. Through a round-trip operation, we can get the node to be deleted, the parent node of the node to be deleted, and whether the node to be deleted is the left node of the parent node.
-
Then there will be several big situations
-
1. If the node to be deleted is a leaf node,
-
2. If the node to be deleted has only one left child node
-
3. If the node to be deleted has only one right child node
-
4. If the node to be deleted has two child nodes
-
Make a judgment according to the above different situations to ensure that after deleting a node, it is still a binary search tree.
(4) Red black tree
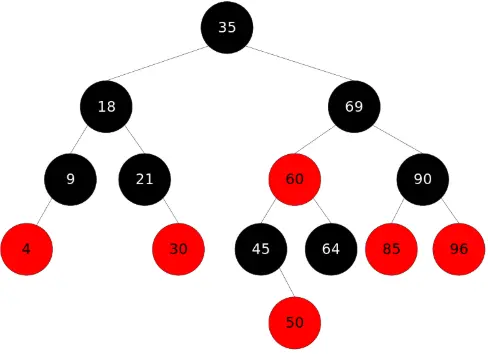
- The thing above is actually a red black tree
- Let's answer first, what is red black tree and why red black tree appears!
- Red black tree is essentially a binary search tree
- It is actually used to solve a problem
- When inserting data into the binary search tree, sometimes the tree formed by the insertion will lose balance, which makes the layer side of the binary search tree very deep
- As we all know, the efficiency of the binary search tree is very related to its hierarchy. Therefore, I must find a way to continuously adjust the binary search tree during the insertion process to make it relatively balanced and stable
- The red black tree is such a relatively balanced and evenly distributed binary search tree!
- Below is an unbalanced binary search tree
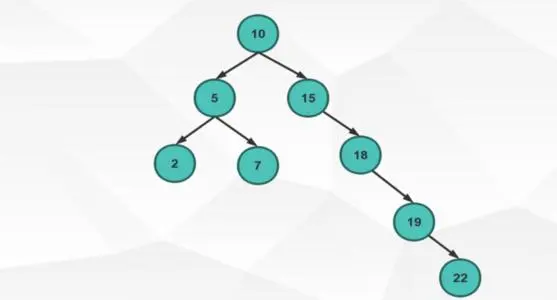
-
It can be seen that if we do not adjust, as long as we insert a larger number that increases more than continuous insertion, it will form a deep structure. In this way, the binary search tree will lose its original meaning.
-
Red black tree is a solution!
-
In other words, as long as the red black tree meets the following rules, it can ensure that the red black tree is a binary search tree with relatively uniform distribution and search efficiency close to the best
-
Every section
-
It's not black
-
It's red
* The root node is always black * If the node is red, its child nodes must be black (otherwise not necessarily) * Each path from root to leaf node * The number of black nodes must be the same
Because the content of red black tree is still relatively responsible, we will introduce red black tree here for the time being. Later, I will write a blog to introduce it in detail.
8, Figure
-
Next, we need to understand an important data structure, graph, and even have a set of special theories to study it in mathematics!

-
Today, we take it out of context and only learn what is helpful for our development.
-
In the data structure of graph, it is composed of nodes and edges. Why does graph appear!
-
In fact, because there are many problems in life, we can abstract them into graphs for research, which can facilitate research and help us analyze them with the help of mathematical tools.
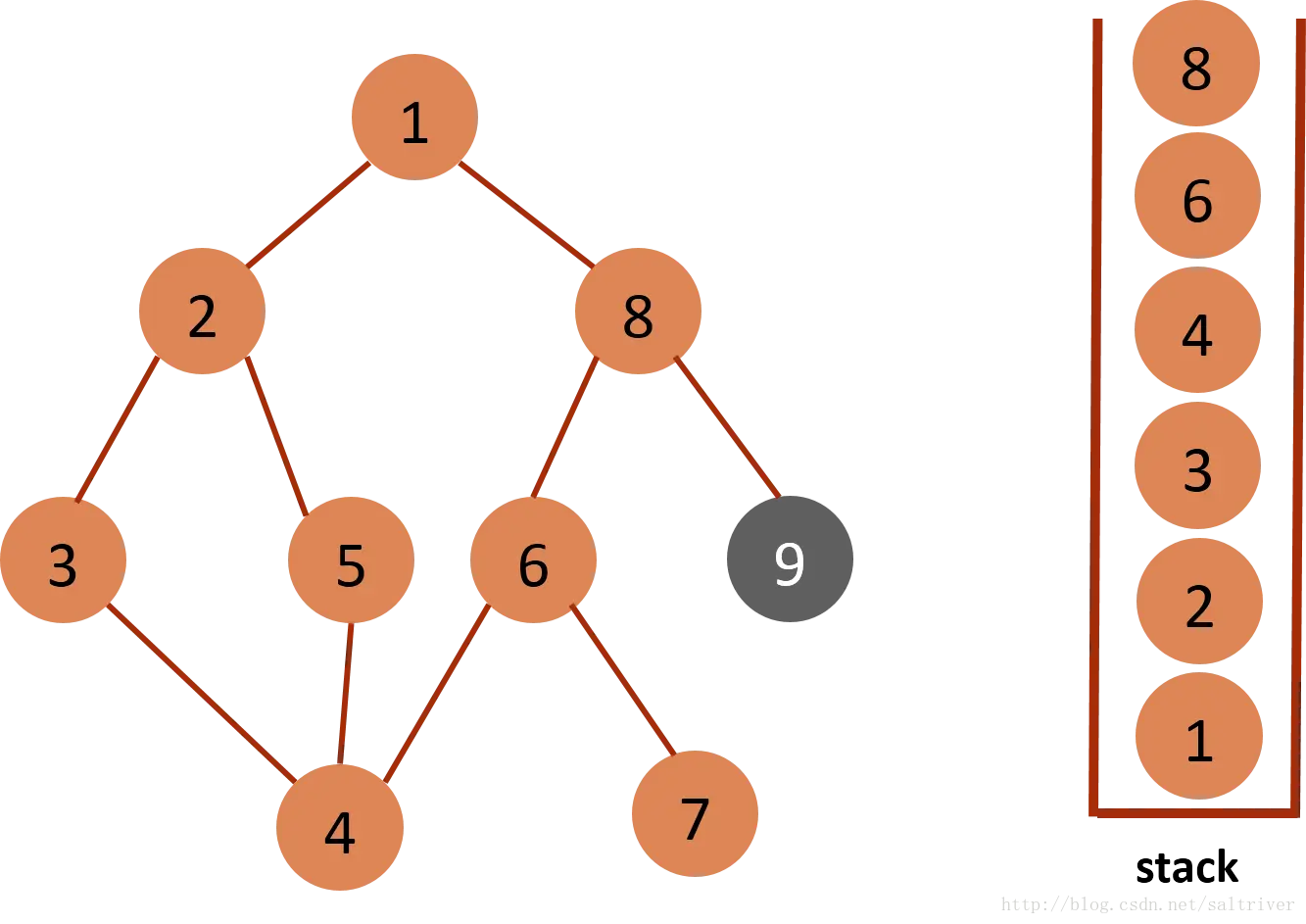
- It will be found that the graph is very similar to the binary search tree, because the binary search tree is actually a graph. The graph is composed of nodes and edges, and any node can point to any node from the edge
- In life, we will encounter the shortest path problem and the minimum cost problem, which can be analyzed with the help of graphs.
- First, we encapsulate the data structure of graph!
class Graph {
constructor() {
this.vertexes = []
this.edges = {}
this.size = 0
this.state = {}
}
addVertex(vertex) {
let list = new List() // The list here is the encapsulated list of the previous article
this.vertexes.push(vertex)
this.edges[[vertex]] = list
this.size++
this.state[vertex] = false
}
addEdge(vertex1, vertex2) {
// Judge if it doesn't exist
this.edges[vertex1].append(vertex2)
this.edges[vertex2].append(vertex1)
return this
}
toString() {
let result = ''
for (var key in this.edges) {
result += key + '=>' + this.edges[key].toString() + '\n'
}
console.log(result);
return result
}
}
9, Traversal algorithm
- In order to traverse the graph structure, we can have two strategies, the first one
- Start traversing from the start node, traverse its child nodes one by one, and then the grandchildren until the nodes in the whole graph are traversed. This method is called breadth first search.
- The second is to start traversing from the start node, traverse its first child node, and then traverse the first child node and the first child node. After this branch traverses, traverse the second child node of the start node and traverse the whole graph. This method is called depth first search, and we also write the method.
- Just add it directly to the previous class!
// BFS breadth first search
bfs(initV, handler) {
let queue = []
queue.push(initV)
// [ 'A','B','C','D'... ]
while (queue.length > 0) {
let targetV = queue.shift()
if (!this.state[targetV]) {
this.edges[targetV].foreach((item) => {
if (!this.state[targetV]) {
queue.push(item)
}
})
handler(targetV)
this.state[targetV] = true
}
}
}
// DFS depth first search
dfs(initV, handler) {
let handleNode = (initV, handler) => {
if (!this.state[initV]) {
handler(initV)
this.state[initV] = true
this.edges[initV].foreach(item => {
if (!this.state[item]) {
handleNode(item, handler)
}
})
}
}
handleNode(initV, handler)
}
10, Sorting algorithm
- Next, we will introduce several sorting algorithms. Each sorting algorithm has its own characteristics!
- Why should we understand the sorting algorithm!
- Because it is very important to change a group of data from disorder to order. It plays an important role in managing and using these data in the future. Therefore, let's learn the sorting algorithm!
(1) Bubble sorting
- First of all, let me explain bubble sorting. Its core is to compare the first one with the second one when there is a set of data. Follow a principle that if who is bigger, change who to the front! Then compare the second with the third! At the end of the first cycle, the last face of this set of data must be a maximum number, and then use the cycle to control where to end the sub cycle. The outer cycle should decrease, because the more to the end, the fewer elements to compare! Finally, there is a sorted data!
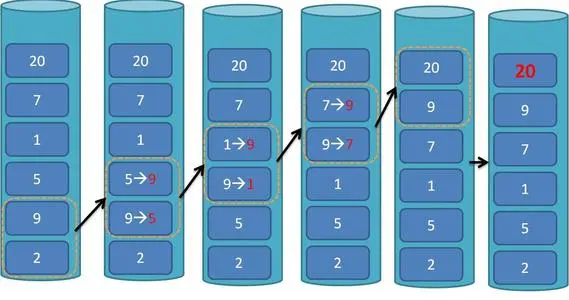
class ArrayList {
constructor(arr = []) {
this.arr = arr
this.size = arr.length
}
insert(ele) {
this.arr.push(ele)
this.size++
}
toString() {
let result = ''
this.arr.forEach((item) => {
result += item + " "
})
return result
}
// change of position
exchange(position1, position2) {
let temp = this.arr[position1]
this.arr[position1] = this.arr[position2]
this.arr[position2] = temp
}
// Bubble sort O(n**2)
bubbleSort() {
for (var j = this.size - 1; j > 0; j--) {
for (var i = 0; i < j; i++) {
if (this.arr[i] > this.arr[i + 1]) {
this.exchange(i, i + 1)
}
}
}
}
}
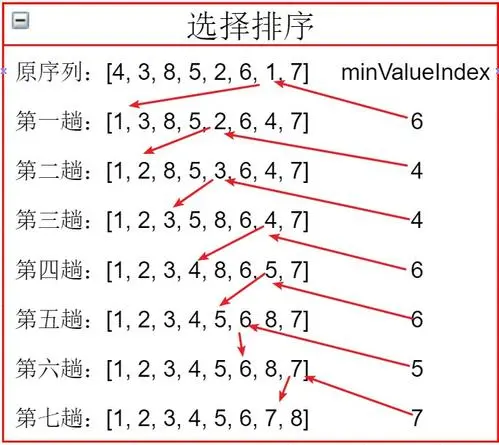
(2) Select sort
- Selective sorting is actually an optimization of bubbling sorting. The main optimization is the number of exchanges. You can imagine bubbling sorting in your mind. First, the inner loop of bubbling sorting will find the largest value and put it in the end, but the final result is formed by many exchanges, If the largest tree is at the top of the data column, That has to be exchanged n-1 times (N generally refers to the length of the list) in order to put the maximum value at the end. The optimization idea of sorting is that since the maximum value is compared, why don't we find the maximum value in the limited range first. After finding it, we only need to exchange it once, and this time directly put the maximum value at the end! Is this much less than the exchange times of bubble sorting? Yes, Let's write it!
class ArrayList {
constructor(arr = []) {
this.arr = arr
this.size = arr.length
}
insert(ele) {
this.arr.push(ele)
this.size++
}
toString() {
let result = ''
this.arr.forEach((item) => {
result += item + " "
})
return result
}
// change of position
exchange(position1, position2) {
let temp = this.arr[position1]
this.arr[position1] = this.arr[position2]
this.arr[position2] = temp
}
// Select sort O(n**2)
chooseSort() {
for (var j = 0; j < this.size; j++) {
let min = j
for (var i = j + 1; i < this.size; i++) {
if (this.arr[min] > this.arr[i]) {
min = i
}
}
this.exchange(min, j)
}
}
}
- Did you find that the first level cycle does not end once, there will be a maximum value position, and then make an exchange,
(3) Insert sort
- The so-called insertion sort is the real optimization of the number of cycles. How to optimize it? Let's explain the insertion sort in detail
- The idea of insertion sorting is to always regard the left side of a group of unordered sequence as ordered, and the first time is the first, because there is only one, so we regard it as ordered.
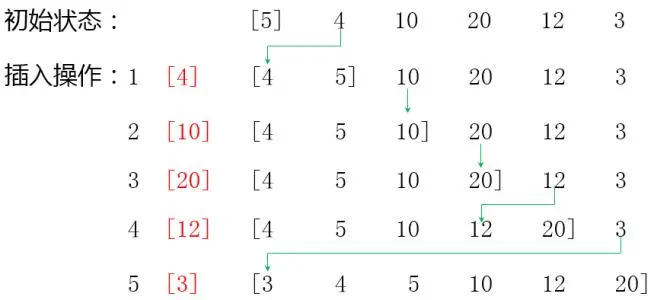
- The second time, take out the second bit and insert it into the ordered sequence on the left, and then traverse the ordered sequence. Because it is ordered, as long as you find the first number smaller than the extracted number and insert it in front of the number, you don't need to traverse the whole sequence. Therefore, the number of cycles can be less than the above two algorithms, So the whole sequence can be ordered until the end.
- All right, let's start writing!
class ArrayList {
constructor(arr = []) {
this.arr = arr
this.size = arr.length
}
insert(ele) {
this.arr.push(ele)
this.size++
}
toString() {
let result = ''
this.arr.forEach((item) => {
result += item + " "
})
return result
}
// change of position
exchange(position1, position2) {
let temp = this.arr[position1]
this.arr[position1] = this.arr[position2]
this.arr[position2] = temp
}
// Insert sort O(n**2)
insertSort() {
for (var i = 1; i < this.size; i++) {
let target = this.arr[i]
for (var j = 0; j < i; j++) {
if (target < this.arr[j]) {
this.exchange(i, j)
break
}
}
}
}
- In fact, the second loop is suggested to be written as a while loop, so there is no need to force break to end the loop
(4) Quick sort
- Next, you can be a little excited! Quick sorting is known as one of the top 10 algorithms in the 20th century.
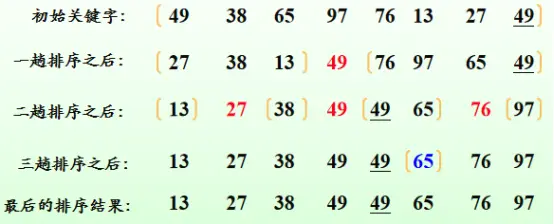
- What is the idea of quick sorting! It's like this!
- From a group of unordered sequences, select any number as middle as possible (that is, the size of this number is almost in the middle of this group of sequences), and then put all the numbers larger than this tree on the right and those smaller than this number on the left
- Then do the same recursive operation for the unordered sequence on the left and right sides
- After recursion, there is an ordered sequence of numbers
- Let's look at the code!
class ArrayList {
constructor(arr = []) {
this.arr = arr
this.size = arr.length
}
insert(ele) {
this.arr.push(ele)
this.size++
}
toString() {
let result = ''
this.arr.forEach((item) => {
result += item + " "
})
return result
}
// Quick sort
quickSort(arr = this.arr) {
if (arr.length == 1 || !arr.length) {
return arr
} else {
let middle = arr[0]
let less = arr.filter(item => item < middle)
let more = arr.filter(item => item > middle)
return [...this.quickSort(less), middle, ...this.quickSort(more)]
}
}
}
- After seeing the code, it's easier to understand! In fact, in addition to these four sorting algorithms, there is also a hill sorting. Interested students can also learn about it! Due to space reasons, I won't introduce it here!