This is [025, the addition of two numbers in the linked list] on LeetCode, and the difficulty is [medium]

subject

Two non empty linked lists l1 and l2 are given to represent two non negative integers. The highest digit is at the beginning of the linked list. Each of their nodes stores only one digit. Adding these two numbers will return a new linked list.

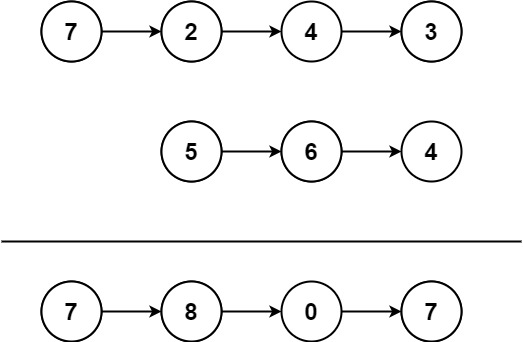
Example

Input: l1 = [7,2,4,3], l2 = [5,6,4]
Output:[7,8,0,7]

Train of thought analysis

Usually, the addition of two integers is to add one digit first, then ten digits, and so on. When adding, you also need to pay attention to the carry. If the sum of the single digits of two integers exceeds 10, a carry will be generated to the ten digits. In the next step of adding the ten digits, you should add this carry

To sum up, we need to start from the tail of the linked list (the single digit is at the tail node). Since the linked list can only be traversed from the beginning, there are two methods (inversion method and stack method)

Solution 1 (stack method)

In the process of traversing the linked list, the nodes are pushed into the stack (last in first out). Therefore, the first node out of the stack is the single digit, and the last node out of the stack is the highest bit

step

1. Define two stacks to store the nodes of two linked lists
2. Traverse the two linked lists, and press the nodes into the stack in turn during the traversal process
3. Define a sumNode node to store the head node of the result linked list. It is initially null
4. Define a variable carry, initially 0, to store the carry after adding a certain digit of two numbers
5. Traversal, the two stacks out of the stack at the same time. If the length of the two linked lists is equal, the two stacks will end when they are empty at the same time. If the length of the two linked lists is not equal, the long stack ends when it is empty. Perform the following operations during traversal
   • Declare a variable sum to store the added value of a certain digit of two numbers
   • Judge whether the stack is empty. If it is empty, let the value of the current node be 0. Because if the length of the two linked lists is not equal, the stack of the short linked list may be empty. Otherwise, the nodes of two stacks will pop up
   • Add the values of the two nodes, add the carry value carry, and assign the result to sum
   • Judge whether the value of sum is > = 10. If > = 10, carry will be generated, so that carry is equal to 1 and sum=sum - 10. Otherwise, let carry be equal to 0 without changing the value of sum
   • Define a new node, newNode, with the value of sum
   • Let the new node point to sumnode (head node), and the new node becomes the head node
   • Reset sumNode as the head node and assign the value of the new node to sumNode
6. Judge whether the value of carry is greater than 0 (when the lengths of the two linked lists are equal, the highest bit may be carried). If it is greater than 0, create a new node with the value of carry, and let the new node point to sumNode as the head node. Then reset sumNode as the head node and assign the value of the new node to sumNode

code implementation

class Solution {
       public ListNode addTwoNumbers(ListNode headA, ListNode headB) {
        // Define two stacks to store the nodes of two linked lists
        Stack<ListNode> stackA = new Stack<>();
        Stack<ListNode> stackB = new Stack<>();
        // Traverse the two linked lists, and press the nodes into the stack in turn during the traversal process
        while (headA != null) {
            stackA.push(headA);
            headA = headA.next;
        }
        while (headB != null) {
            stackB.push(headB);
            headB = headB.next;
        }
        // Define a sumNode node to store the head node of the result linked list. It is initially null
        ListNode sumNode = null;
        // Define a variable carry, initially 0, to store the carry after adding a certain digit of two numbers
        int carry = 0;
        /*Traversal, the two stacks out of the stack at the same time. If the length of the two linked lists is equal, the two stacks will end when they are empty at the same time
          If the length of the two linked lists is not equal, the long stack ends when it is empty*/
        while (!stackA.isEmpty() || !stackB.isEmpty()) {
            /* Declare a variable sum to store the added value of a certain digit of two numbers Determine whether the stack is empty before adding,
               If it is empty, let the value of the current node be 0. Because if the length of the two linked lists is not equal, the stack of the short linked list may be empty.
               Otherwise, the nodes of two stacks will pop up*/
            int sum = (stackA.isEmpty() ? 0 : stackA.pop().val) + (stackB.isEmpty() ? 0 : stackB.pop().val) + carry;
            // Judge whether the value of sum is > = 10. If > = 10, carry will be generated and carry will be equal to 1
            carry = sum >= 10 ? 1 : 0;
            // Judge whether the value of sum is > = 10. If > = 10, let sum=sum - 10. Otherwise, do not change the value of sum
            sum = sum >= 10 ? sum - 10 : sum;
            // Define a new node, newNode, with the value of sum
            ListNode newNode = new ListNode(sum);
            // Let the new node point to sumnode (head node), and the new node becomes the head node
            newNode.next = sumNode;
            // Reset sumNode as the head node and assign the value of the new node to sumNode
            sumNode = newNode;
        }
        /* Judge whether the value of carry is greater than 0 (when the lengths of the two linked lists are equal, the addition of the highest bits may carry),
            If greater than, create a new node with the value of carry
            And let the new node point to sumNode as the head node, then reset sumNode as the head node, and assign the value of the new node to sumNode*/
        if (carry > 0) {
            ListNode newNode = new ListNode(carry);
            newNode.next = sumNode;
            sumNode = newNode;
        }
        // Returns the head node of the result linked list
        return sumNode;
    }
}

Node class

public class ListNode<T> {

    T val;
    ListNode next;

    public ListNode() {

    }

    public ListNode(T val) {
        this.val = val;
    }

    public ListNode(T val, ListNode next) {
        this.next = next;
    }
}

Test code

public class Test {

    @org.junit.Test
    public void test1() {
        ListNode headA = new ListNode(9);
        ListNode one = new ListNode(8);
        ListNode two = new ListNode(4);
        headA.next = one;
        one.next = two;

        ListNode headB = new ListNode(1);
        ListNode first = new ListNode(8);
        headB.next = first;

        ListNode sumHead = new Solution().addTwoNumbers1(headA, headB);

        System.out.print("984 + 18 = ");
        while (sumHead != null) {
            System.out.print(sumHead.val);
            sumHead = sumHead.next;
        }
    }
}

Complexity analysis

Suppose the length of the two linked lists is n,m

Time complexity:

When traversing two linked list stacks initially, the time complexity is O(n+m). When traversing two stacks at the same time, the time complexity is O(n) or O(m), so the total time complexity is O(n+m) + O(n) or O(m) = O(n+m)

Space complexity:

Two stacks need to be declared to store two linked list nodes, so the space complexity is O(n+m)

Solution 2 (reverse linked list)

The head node of the inverted linked list represents the single digit, and the tail node represents the highest digit. At this time, adding from the head node of the two linked lists is equivalent to adding from the single digit of an integer, Reverse linked list It has been given in previous articles and will not be described here

step

1. Reverse two linked lists

2. Define a sumNode node to store the head node of the result linked list. It is initially null

3. Define a variable carry, initially 0, to store the carry after adding a certain digit of two numbers

4. Traverse two linked lists at the same time. If the length of the two linked lists is equal, it ends when traversing the two linked lists at the same time. If the length of the two linked lists is not equal, it ends when traversing the long linked list. Perform the following operations during traversal

   • Declare a variable sum to store the added value of a certain digit of two numbers

   • Judge whether the current node is null. If it is null, let the value of the null node be 0. Because if the length of the two linked lists is not equal, the current node of the short linked list may be null.

   • Add the values of the current nodes of the two linked lists and add the carry value carry, and the result is assigned to sum

   • Judge whether the value of sum is > = 10. If > = 10, carry will be generated, so that carry is equal to 1 and sum=sum - 10. Otherwise, let carry be equal to 0 without changing the value of sum

   • Define a new node, newNode, with the value of sum

   • Let the new node point to sumnode (head node), and the new node becomes the head node

   • Reset sumNode as the head node and assign the value of the new node to sumNode

   • Reset the current node and take the next node of the current node as the current node to realize traversal

5. Judge whether the value of carry is greater than 0 (when the lengths of the two linked lists are equal, the highest bit may be carried). If it is greater than 0, create a new node with the value of carry, and let the new node point to sumNode as the head node. Then reset sumNode as the head node and assign the value of the new node to sumNode

code implementation

class Solution {
       public ListNode addTwoNumbers(ListNode headA, ListNode headB) {
        // Reverse two linked lists
        headA = reverseList(headA);
        headB = reverseList(headB);
        // Add each bit after inversion, and the result is the sum of two
        ListNode sumReverse = addReverse(headA, headB);
        // Return the result
        return sumReverse;
    }

    // Reverse linked list method
    public ListNode reverseList(ListNode headA) {
        ListNode preNode = null;
        ListNode currNode = headA;
        while (currNode != null) {
            ListNode nextNode = currNode.next;
            currNode.next = preNode;
            preNode = currNode;
            currNode = nextNode;
        }
        return preNode;
    }

    public ListNode addReverse(ListNode headA, ListNode headB) {
        // Define a sumNode node to store the head node of the result linked list. It is initially null
        ListNode sumNode = null;
        // Define a sumNode node to store the head node of the result linked list. It is initially null
        int carry = 0;
        // Traverse two linked lists at the same time. If the length of the two linked lists is equal, it will end when traversing the linked list. If the length of the two linked lists is not equal, it ends when traversing the long linked list
        while (headA != null || headB != null) {
            /* Declare a variable sum to store the added value of some digit of two numbers, and add carry. Judge whether the current node is null before adding
               If it is null, let the value of the null node be 0. Because if the length of the two linked lists is not equal, the current node of the short linked list is null.*/
            int sum = (headA == null ? 0 :headA.val) + (headB == null ? 0 : headB.val) + carry;
            // Judge whether the value of sum is > = 10. If > = 10, carry will be generated and carry will be equal to 1
            carry = sum >= 10 ? 1 : 0;
            // Judge whether the value of sum is > = 10. If > = 10, let sum=sum - 10. Otherwise, do not change the value of sum
            sum = sum >= 10 ? sum - 10 : sum;
            // Define a new node, newNode, with the value of sum
            ListNode newNode = new ListNode(sum);
            // Let the new node point to sumnode (head node), and the new node becomes the head node
            newNode.next = sumNode;
            // Reset sumNode as the head node and assign the value of the new node to sumNode
            sumNode = newNode;
            // Reset the current node and take the next node of the current node as the current node to realize traversal
            headA = headA == null ? null :headA.next;
            headB = headB == null ? null :headB.next;
        }
        /* Judge whether the value of carry is greater than 0 (when the lengths of the two linked lists are equal, the addition of the highest bits may carry),
            If greater than, create a new node with the value of carry
            And let the new node point to sumNode as the head node, then reset sumNode as the head node, and assign the value of the new node to sumNode*/
        if (carry > 0) {
            ListNode newNode = new ListNode(carry);
            newNode.next = sumNode;
            sumNode = newNode;
        }
        // Returns the head node of the result linked list
        return sumNode;
    }
}

Complexity analysis

Suppose two linked list length bits n,m

Time complexity:

When initially traversing and reversing two linked lists, the time complexity bits are O(n) and O(m). When calculating the sum of two numbers, it is necessary to traverse two linked lists at the same time. Therefore, the time complexity bit is O(n) or O(m), and the total time complexity is O(n) + O(m) + O(n) or O(m) = O(n)

Space complexity:

Only a few fixed nodes are declared, so the spatial complexity is O (1);