Note:

Title:

Give you an n x n matrix, in which the elements of each row and column are sorted in ascending order to find the k-smallest element in the matrix.

Note that it is the k-th smallest element after sorting, not the k-th different element.

Example 1:
Input: matrix = [[1,5,9],[10,11,13],[12,13,15]], k = 8
Output: 13
Explanation: the elements in the matrix are [1,5,9,10,11,12,13,13,15], and the 8th small element is 13
Example 2:
Input: matrix = [[-5]], k = 1
Output: - 5

Tips:
n == matrix.length
n == matrix[i].length
1 <= n <= 300
-109 <= matrix[i][j] <= 109
The topic data ensures that all rows and columns in the matrix are arranged in non decreasing order
1 <= k <= n2

Solution:
Method a heap sort (merge sort)
Ideas and algorithms
According to the properties given by the title, each row of the matrix is an ordered array. The problem is to find the k-th largest number from the n ordered arrays. We can think of using the method of merging and sorting, and merging to the k-th number can stop.

The general merge sort is the merging of two arrays, while this problem is the merging of n arrays, so it needs to be maintained with a small root heap to optimize the time complexity.

For details on how to merge, please refer to force deduction 23 Merge K sorted linked lists.

Complexity analysis
Time complexity: O(klogn), merging k times. The time complexity of each heap insert and pop-up operation is logn.
Space complexity: O(n), the size of the heap is always n.

class Solution {
public:
    int kthSmallest(vector<vector<int>>& matrix, int k) {
        class point{
            public:
                int val,x,y;
                point(int val_,int x_,int y_):val(val_),x(x_),y(y_){};
        };
        class compare{
            public:
                bool operator() (const point &a,const point &b) {
                    return a.val>b.val;
                }
        };
        priority_queue<point,vector<point>,compare> points;
        int row=matrix.size();
        int col=matrix[0].size();
        for(int i=0;i<row;i++){
            points.emplace(matrix[i][0],i,0);
        }
        for(int i=0;i<k-1;i++){
            point t=points.top();
            points.pop();
            if(t.y+1==col){
                continue;
            }
            points.emplace(matrix[t.x][t.y+1],t.x,t.y+1);
        }
        return points.top().val;
    }
};

Method binary search
Ideas and algorithms

According to the properties given in the title, the elements in this matrix increase from top left to bottom right (assuming that the upper left corner of the matrix is matrix[0][0]). The following figure is an example:

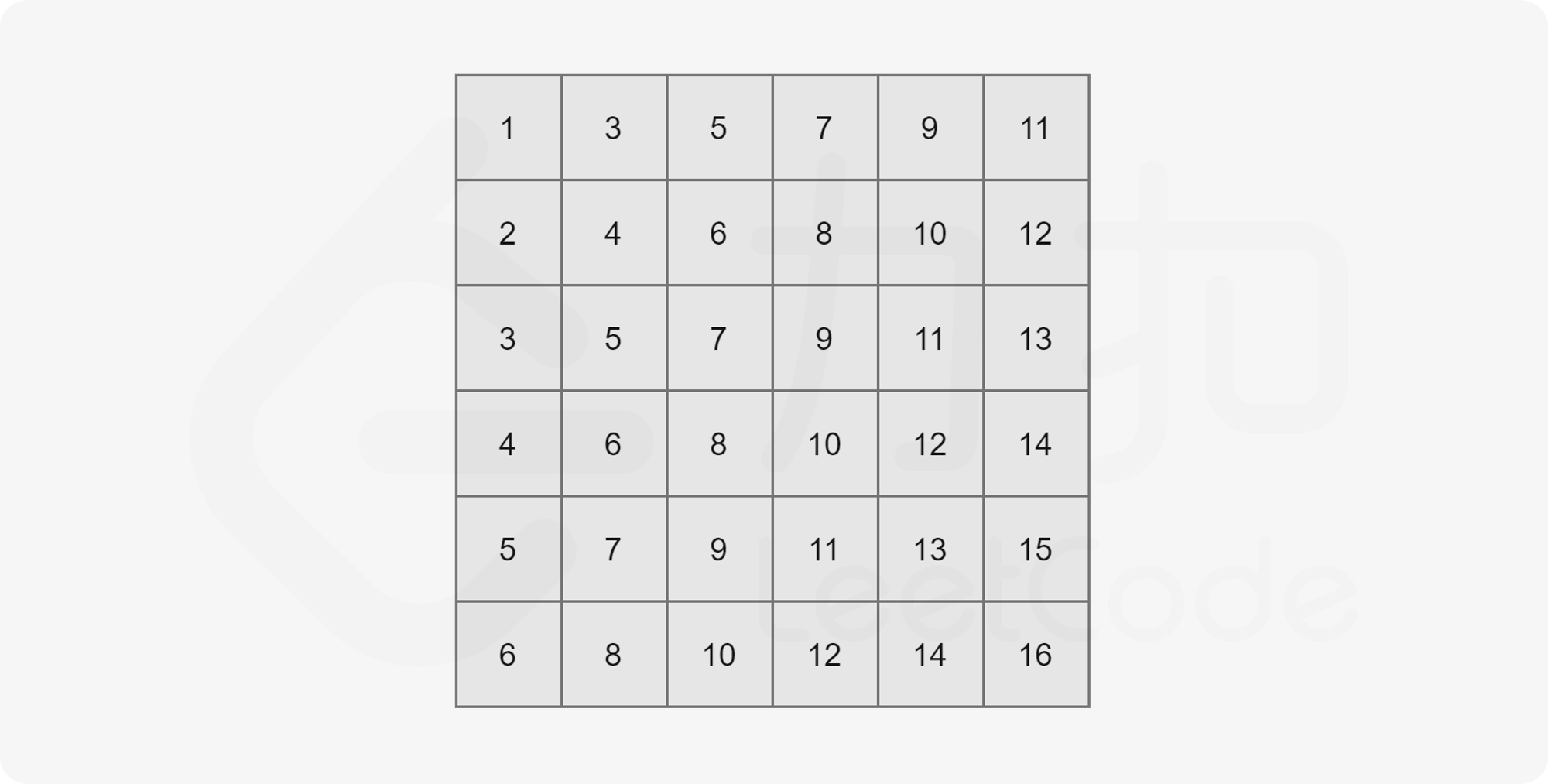
We know that matrix[0][0] is the minimum value and matrix[n − 1][n − 1] is the maximum value in the whole two-dimensional array. Now we record them as l and r respectively.

We can find a property: if any number mid satisfies l ≤ mid ≤ r, then all the numbers not greater than mid in the matrix must be distributed in the upper left corner of the matrix.

For example, in the following figure, take mid=8:

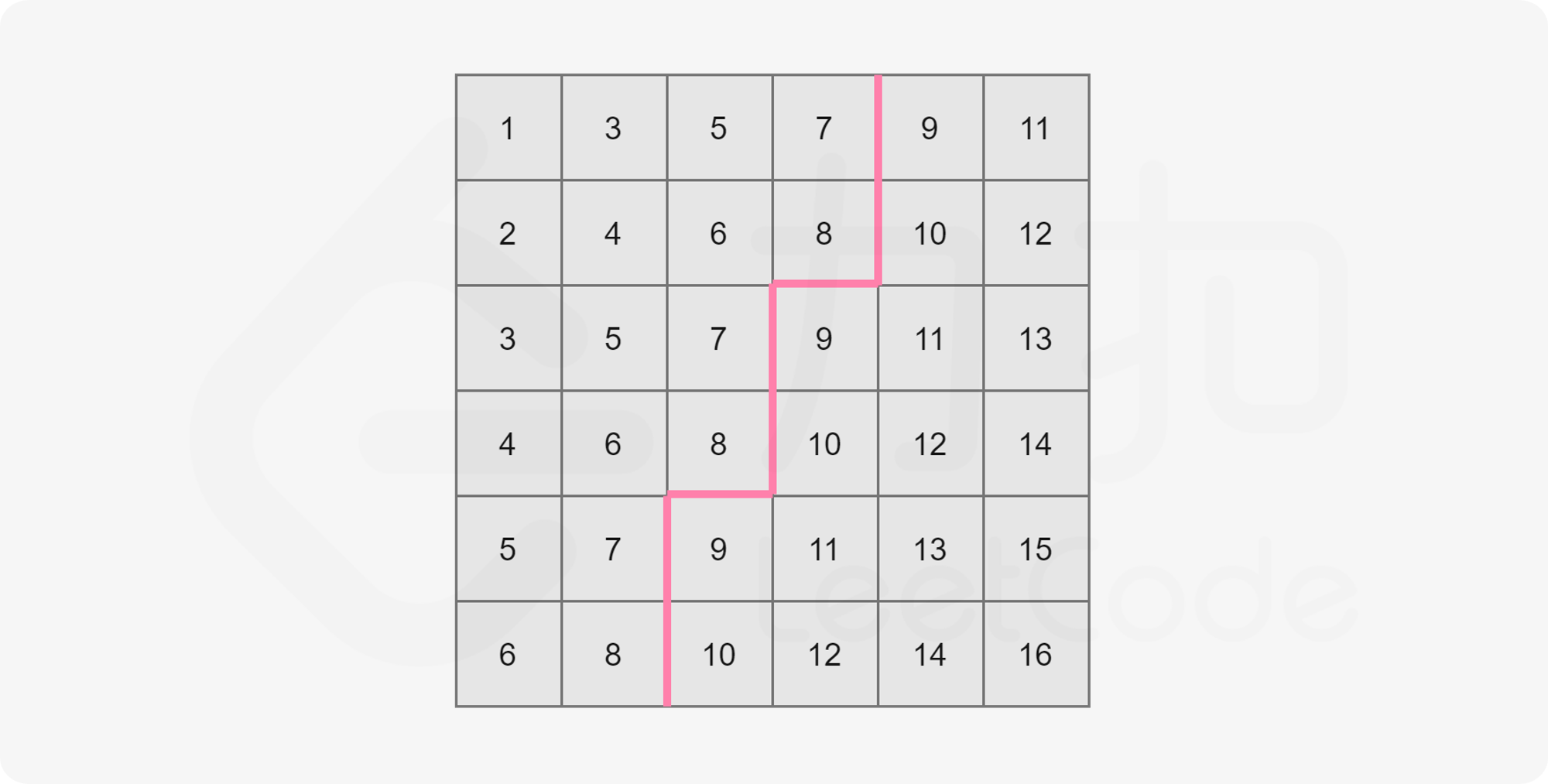
We can see that the number greater than mid and the number not greater than mid in the matrix form two plates respectively, and separate the rectangle along a sawtooth line. The size of the upper left corner plate is the number not greater than mid in the matrix.

Readers can also take some mid values and draw pictures to deepen their understanding.

As long as we walk along this zigzag line once, we can calculate the size of the two plates, and naturally count the number not greater than mid in this matrix.

The walking method is shown as follows, and mid=8 is still taken:

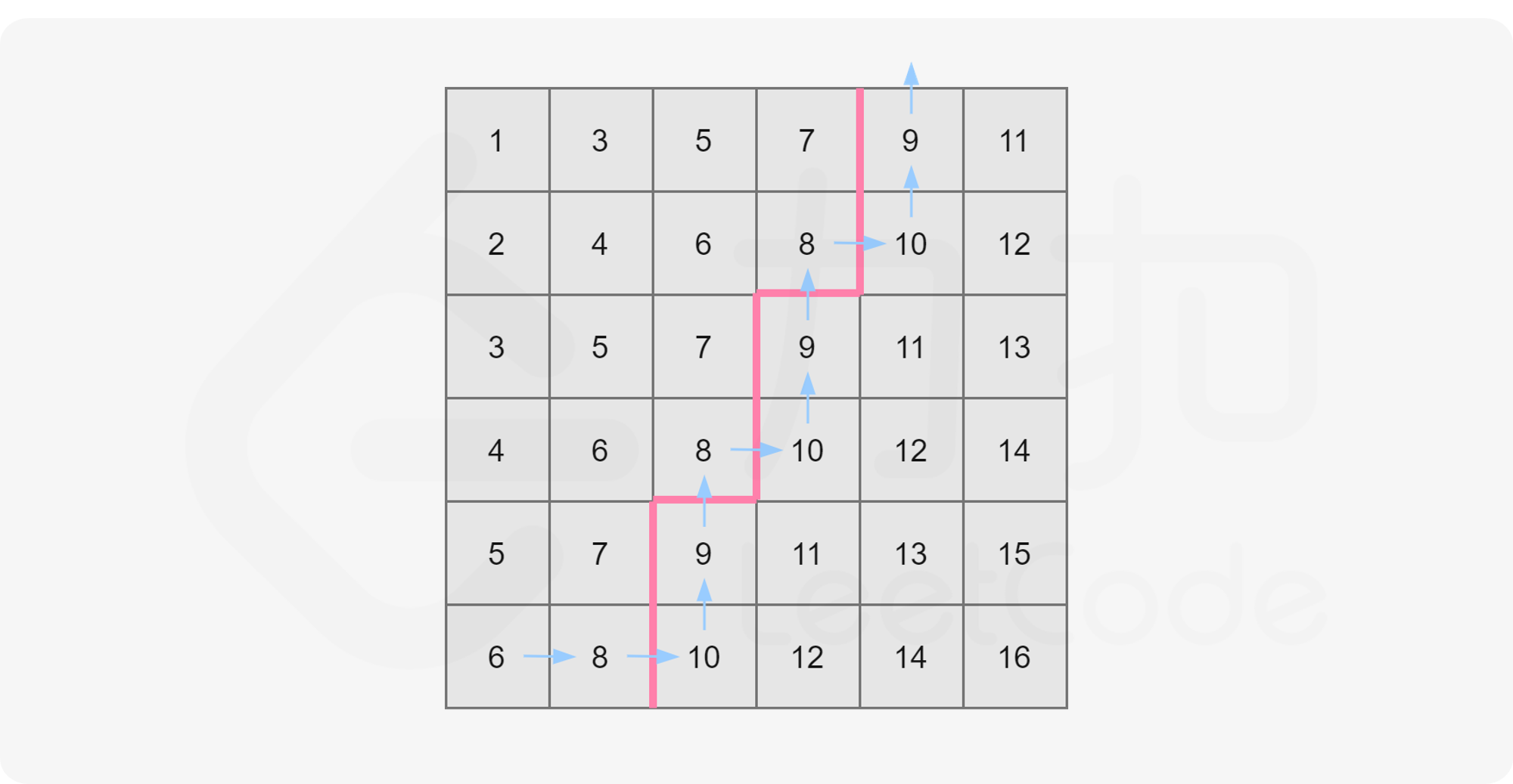
The walking method can be described as follows:

1. The initial position is matrix[n - 1][0] (i.e. lower left corner);
2. Set the current position as matrix[i][j]. If matrix[i][j] ≤ mid, the number of numbers not greater than midmid in the current column (i.e. i+1) will be accumulated into the answer and moved to the right, otherwise it will move up;
3. Keep moving until you get out of the grid.

We find that the time complexity of this walking method is O(n), that is, we can calculate linearly how many numbers in the matrix are not greater than any mid. This satisfies the nature of binary search.

Suppose the answer is x, then you can know l ≤ x ≤ r, which determines the upper and lower bounds of binary search.

Each time for the answer mid of "guess", calculate how many numbers in the matrix are not greater than mid:

1. If the number is not less than k, it indicates that the final answer x is not greater than mid;
2. If the number is less than k, the final answer x is greater than mid.

So we can calculate the final result x.

Complexity analysis
Time complexity: O(nlog(r − l)), the number of binary lookups is O(log(r − l)), and the time complexity of each operation is O(n).
Space complexity: O(1).

class Solution {
public:
    bool check(vector<vector<int>> matrix,int mid,int k){
        int i=matrix.size()-1;
        int j=0;
        int count=0;
        while(i>=0&&j<matrix[0].size()){
            if(matrix[i][j]<=mid){
                j++;
                count+=(i+1);
            }
            else{
                i--;
            }
        }
        return k<=count;
    }
    int kthSmallest(vector<vector<int>>& matrix, int k) {
        int left=matrix[0][0];
        int right=matrix[matrix.size()-1][matrix.size()-1];
        while(left<right){
            int mid=left+(right-left)/2;
            if(check(matrix,mid,k)==true){
                right=mid;
            }
            else{
                left=mid+1;
            }
        }
        return left;
    }
};