Background description
Some time ago, there was a need to find out whether the point is inside the polygon, which has been tossed for a lot of time. Now we intercept the key part - finding the horizontal direction like the largest rectangle inside the arbitrary polygon - to make a blog.
The algorithm is easy to find out whether the point is inside the polygon, but when the amount of data is large, the algorithm must be optimized. An obvious optimization point is to find the maximum inscribed rectangle. After all, if the judgment point is in the rectangle, only four judgment statements need to be executed at most, and the execution speed is very fast; To judge a polygon, you need to compare it with each edge. It will be much slower than a rectangle. Especially when doing GIS data, it is basically all complex polygons.
The original algorithm is here: https://www.cnblogs.com/naaoveGIS/p/7218634.html
Although the original article wrote the chapter of algorithm implementation, it is actually an empty shell, and the real implementation still depends on itself. It is described in detail below.
Algorithm flow
Now that you want to implement it, here is a list of the original algorithm flow.
- Step 1: obtain the quadrangular coordinates of an arbitrary polygon, construct a rectangle through the quadrangular coordinates, and divide the rectangle into M*N regular grids;
- Step 2: traverse all grids and judge the inclusion relationship between each grid and polygon. If the grid is in a polygon, it is marked as 1, otherwise it is 0;
- Step 3: calculate the largest rectangle composed of 1 among the rectangles composed of 0 and 1;
- Step 4: get the quadrangular coordinates represented by the largest rectangle and construct a real geographic rectangle.
The original author put forward two points for attention. One is that the third step is difficult, and the other is that the rectangular division granularity in the first step is determined according to the required accuracy.
The third step is really difficult, but it's basically a lot of search, and it's posted here leetcode 85. Maximum rectangle , this problem is to find the maximum rectangular area. With a little change, you can get the quadrangular coordinates of the maximum rectangle. Then the second point is to select the accuracy according to the actual project requirements and hardware configuration.
Algorithm implementation
Note: This article uses groovy to realize the seamless connection with java. At the same time, it can be used as a script language to make it easy.
First, define several entity classes, namely point, rectangle and polygon:
class Point {
/**
* Longitude
*/
def lon
/**
* Latitude
*/
def lat
}
class Rectangle {
/**
* Minimum longitude
*/
def minLon
/**
* Maximum longitude
*/
def maxLon
/**
* Minimum latitude
*/
def minLat
/**
* Maximum latitude
*/
def maxLat
}
class MultiPolygon {
/**
* The maximum inscribed rectangle of a polygon
*/
List<Rectangle> largestEnclosingRectangle
/**
* Polygon data points
*/
List<Point> points
}
The maximum inscribed rectangle of a polygon is placed in a List because multiple inscribed rectangles may be required later to improve efficiency.
Step 1: divide the rectangle
Dividing the rectangle is to find the minimum circumscribed rectangle of the polygon first, and then divide the minimum circumscribed rectangle. It is too simple to find the minimum circumscribed rectangle, that is, traverse each point of the polygon to find the maximum / minimum longitude and latitude. The code is as follows:
/**
* Gets the smallest circumscribed rectangle of a polygon area
*/
static Rectangle computeMinimumEnclosingRectangle(List<Point> pts) {
def rec = new Rectangle(
minLon: Double.MAX_VALUE, maxLon: Double.MIN_VALUE,
minLat: Double.MAX_VALUE, maxLat: Double.MIN_VALUE)
pts.each { p ->
rec.minLon = [p.lon, rec.minLon].min()
rec.maxLon = [p.lon, rec.maxLon].max()
rec.minLat = [p.lat, rec.minLat].min()
rec.maxLat = [p.lat, rec.maxLat].max()
}
rec
}
After obtaining the minimum circumscribed rectangle, in order to make the data look better, first standardize its coordinates according to accuracy. Assuming that the precision of the small rectangle you are going to divide is two digits after the decimal point, it is best to make the coordinates of the circumscribed smallest rectangle two digits after the decimal point. The idea is very simple. Small ones can go smaller and large ones can go larger. The code is as follows:
//1. Standardize the rectangle according to the segmentation scale
def minLon = floor(rec.minLon, scale), maxLon = ceil(rec.maxLon, scale),
minLat = floor(rec.minLat, scale), maxLat = ceil(rec.maxLat, scale)
private static def ceil(d, scale) {
def n = (1 / scale) as int
(BigDecimal) Math.ceil(d * n) / n
}
private static def floor(d, scale) {
def n = (1 / scale) as int
(BigDecimal) Math.floor(d * n) / n
}
If double is used in the actual measurement, strange accuracy problems will occur, such as 25.1 + 0.01 = 25.110000000000003, 25.2-0.01 = 25.189999999999998. This problem will occur in C, python, java and groovy. It is not difficult to solve. Add ceil and floor functions according to the required accuracy. But it's better to use BigDecimal directly, as long as you manage the memory well.
After getting the standardized circumscribed minimum rectangle, cut it directly according to the accuracy. Note that after I cut here, I save not rectangles, but data points in order, because rectangles are continuous up, down, left and right except the edges. Saving rectangles will lead to the subsequent calculation of a data point four times, which is not cost-effective. Let's talk about how to convert the data point matrix to a rectangular matrix.
First, look at a segmented rectangle intuitively:
Suppose the matrix for storing rectangular data is rec [] [], and the matrix for storing data points is dot [] [].
Look at the rectangle ① in the upper left corner of the figure. It is rec[0][0]; If you look at the data point in the top left corner, it is dot[0][0]. If you look for a few points, you will find that the coordinate [i][j] of the matrix in rec is equal to the coordinate of the point in the top left corner in dot. Knowing the top left corner will naturally know the data points of the whole rectangle.
If you look at a data point dot[i][j], its rectangular (if any) coordinates in four directions should be as follows (assuming that the middle point is dot[i][j]):

The code is as follows. It is basically an equidistant division. In fact, you can directly operate equidistant without storing the divided data points, but the operation is a little troublesome and can save a little memory.
/**
* The lattice of the segmentation matrix is obtained according to the rectangle and the segmentation scale
* In order to reduce the amount of calculation, the output here is not a real rectangle. Because it is equidistant continuous segmentation, the segmented data points can be directly output, with the data points in the upper left corner as the target
*/
private static List<List<Point>> computeRegionalSlices(Rectangle rec, scale) {
//1. Standardize the rectangle according to the segmentation scale
def minLon = floor(rec.minLon, scale), maxLon = ceil(rec.maxLon, scale),
minLat = floor(rec.minLat, scale), maxLat = ceil(rec.maxLat, scale)
//2. Segmentation (due to human habits, it is tentatively divided by line from top to bottom, that is, from large to small according to latitude and from small to large according to longitude)
List<List<Point>> matrix = []
for (def posLat = maxLat; posLat >= minLat; posLat -= scale) {
List<Point> row = []
for (def posLon = minLon; posLon <= maxLon; posLon += scale) {
row << new Point(lon: posLon, lat: posLat)
}
matrix << row
}
matrix
}
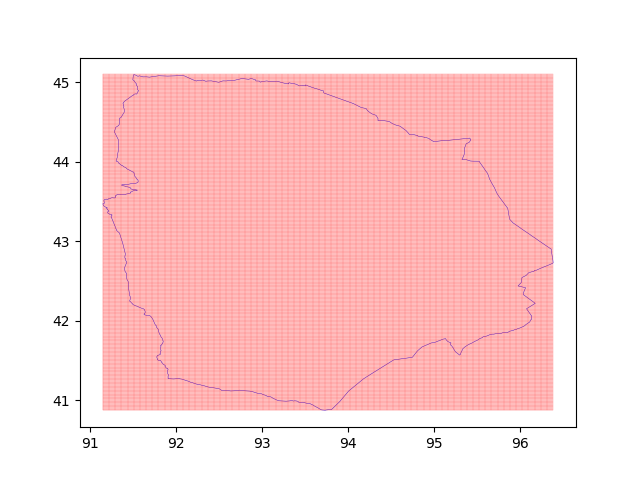
Here are some actual segmentation diagrams.
whole:
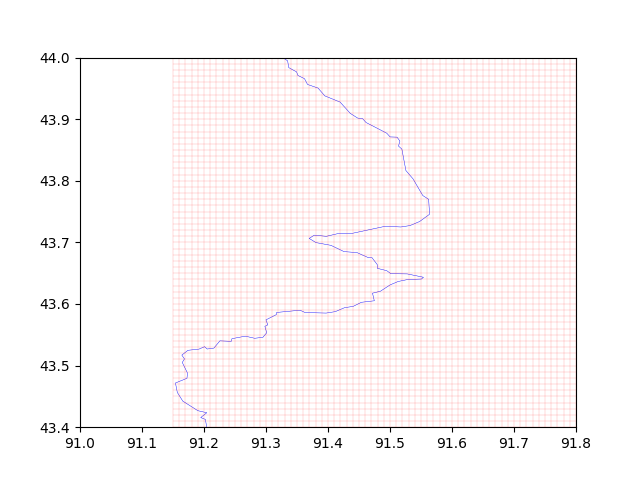
Local details:
Step 2: traverse the mesh and mark it. Mark 1 in the polygon, not 0
This step is relatively simple. Mark according to the four rectangles corresponding to one point above. The code is as follows:
/**
* The marking matrix is calculated according to the segmented rectangle and polygon
*/
private static int[][] computeMarkMatrix(List<Point> pts, List<List<Point>> regionalSlices) {
def m = regionalSlices.size(), n = regionalSlices[0].size(),
rectangleMarks = new int[m - 1][n - 1]
//First mark all the rectangular marking matrices as 1, and then mark the matrices not in the polygon as 0 according to the dot matrix calculation
rectangleMarks.each { Arrays.fill(it, 1) }
//Traverse each point of the tangent lattice to obtain the marking matrix
def inRange = { num, min, max -> num >= min && num <= max }
(0..<m).each { posM ->
(0..<n).each { posN ->
def p = regionalSlices[posM][posN]
//Handles points that are not inside a polygon
if (!isPolygonContainsPoint(pts, p)) {
//The point is not inside the polygon. Process the matrix in four directions corresponding to the point. The row range is [0, m-2], and the column range is [0, n-2]
//Upper left corner [posM-1, posN-1]
if (inRange(posM - 1, 0, m - 2) && inRange(posN - 1, 0, n - 2)) {
rectangleMarks[posM - 1][posN - 1] = 0
}
//Upper right corner [posM-1, posN]
if (inRange(posM - 1, 0, m - 2) && inRange(posN, 0, n - 2)) {
rectangleMarks[posM - 1][posN] = 0
}
//Lower left corner [posM, posN1-1]
if (inRange(posM, 0, m - 2) && inRange(posN - 1, 0, n - 2)) {
rectangleMarks[posM][posN - 1] = 0
}
//Lower right corner [posM, posN]
if (inRange(posM, 0, m - 2) && inRange(posN, 0, n - 2)) {
rectangleMarks[posM][posN] = 0
}
}
}
}
rectangleMarks
}
/**
* Returns whether a point is within a polygonal area (open interval)
*/
static Boolean isPolygonContainsPoint(List<Point> pts, Point p) {
int nCross = 0
pts.size().times { i ->
//Algorithm idea: take any edge of the polygon, make the horizontal extension line of the point, and solve the number of intersections with the current edge. Here, only the intersection on the right of the solution point is found
def p1 = pts[i], p2 = pts[(i + 1) % pts.size()]
//p1p2 is a horizontal line segment with either no intersections or infinite intersections
if (p1.lat == p2.lat) {
return
}
//point at p1p2 bottom or top -- > no intersection
if (p.lat < [p1.lat, p2.lat].min() || p.lat >= [p1.lat, p2.lat].max()) {
return
}
//Solve the X coordinate of the intersection of the point horizontal line and the current p1p2 edge
double x = p1.lon + (p2.lon - p1.lon) * (p.lat - p1.lat) / (p2.lat - p1.lat)
//Only unilateral intersections are recorded. Here, only the intersections to the right of the points are recorded
if (x > p.lon) {
++nCross
}
}
//The intersection points are odd, and the points are in the polygon; The opposite is the opposite
nCross % 2 == 1
}
Note that the 01 matrix is returned in this step, because it will be troublesome to calculate the maximum rectangle in the next step.
Step 3: calculate the maximum rectangle
In this step, just look at the LeetCode algorithm above. Only a few lines are added here to record the coordinates of the maximum matrix:
/**
* Find the maximum rectangle according to the marking matrix, and return [minimum row mark maximum row mark minimum column mark maximum column mark maximum area]
*/
static def maximalRectangle(int[][] matrix) {
def m = matrix.length, n = matrix[0].length
int[][] left = new int[m][n]
(0..<m).each { i ->
(0..<n).each { j ->
if (matrix[i][j] == 1) {
left[i][j] = (!j ? 0 : left[i][j - 1]) + 1
}
}
}
def minC = -1, maxC = -1, minR = -1, maxR = -1, ret = 0
(0..<n).each { j -> // For each column, a histogram based approach is used
int[] up = new int[m]
int[] down = new int[m]
Deque<Integer> stack = new LinkedList<>() //Chain stack
for (int i = 0; i < m; i++) {
while (!stack.isEmpty() && left[stack.peek()][j] >= left[i][j]) {
stack.pop()
}
up[i] = stack.isEmpty() ? -1 : stack.peek()
stack.push(i)
}
stack.clear()
for (int i = m - 1; i >= 0; i--) {
while (!stack.isEmpty() && left[stack.peek()][j] >= left[i][j]) {
stack.pop()
}
down[i] = stack.isEmpty() ? m : stack.peek()
stack.push(i)
}
for (int i = 0; i < m; i++) {
int height = down[i] - up[i] - 1
int area = height * left[i][j]
//Record the position of the largest rectangle
if (area > ret) {
ret = area
minC = up[i] + 1
maxC = down[i] - 1
minR = j - left[i][j] + 1
maxR = j
}
}
}
return [minC, maxC, minR, maxR, ret]
}
Because groovy can return multiple values, the above code directly returns the minimum / maximum row / column mark of the largest rectangle in the rectangular matrix, and returns the area of the rectangle.
Step 4: get the actual coordinates
This step is very easy. You can deduce it a little according to the above figures, and just one line of code:
new Rectangle(minLon: regionalSlices[0][minR].lon, maxLon: regionalSlices[0][maxR + 1].lon,
minLat: regionalSlices[maxC + 1][0].lat, maxLat: regionalSlices[minC][0].lat)
Here are some renderings.
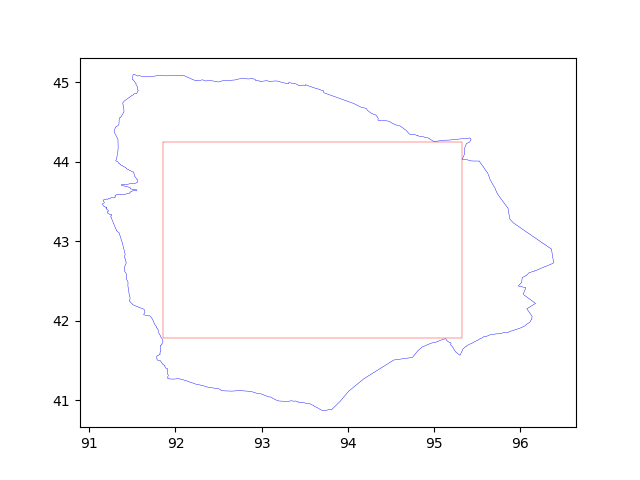
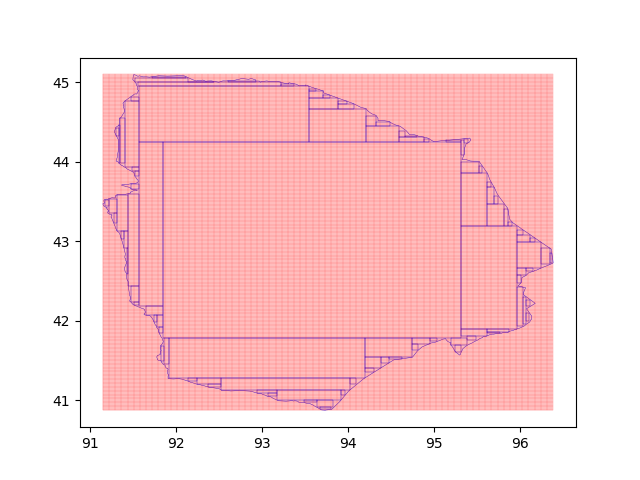
The largest rectangle in the middle is the largest inscribed rectangle, and then I calculated. In this figure, the coverage area of the largest rectangle is only about 56%, so it can be cut according to the area requirements or other requirements.
The complete code is put below. There is also an algorithm for expanding polygons, which is also one of my requirements. I won't elaborate here.
package com.fiberhome.utils.position
import com.fiberhome.utils.position.base.Point
import com.fiberhome.utils.position.base.Rectangle
import com.fiberhome.utils.position.base.ScopeOfCity
import groovy.util.logging.Slf4j
import java.text.DecimalFormat
/**
* created with IntelliJ IDEA 2020.3
* author: hxw
* date: 2021/8/12 9:46
* version: 1.0
* description:
* Location tools
*/
@Slf4j
class PositionUtils {
/**
* Polygon expansion algorithm, algorithm reference: https://blog.csdn.net/lweiyue/article/details/103033630
*
* @param pts For polygons to be expanded, the number of sides shall not be less than 3
* @param expand Distance to be extended
*/
static List<Point> polygonExpand(List<Point> pts, double expand) {
def ans = []
def norm = { x, y -> Math.sqrt(x * x + y * y) }
def df = { x ->
def df = new DecimalFormat('#.######')
df.format(x) as double
}
pts.eachWithIndex { p, index ->
def p1 = pts[index - 1], p2 = pts[(index + 1) % pts.size()]
double v1x = p1.lon - p.lon
double v1y = p1.lat - p.lat
double n1 = norm(v1x, v1y)
double vv1x = v1x / n1
double vv1y = v1y / n1
double v2x = p2.lon - p.lon
double v2y = p2.lat - p.lat
double n2 = norm(v2x, v2y)
double vv2x = v2x / n2
double vv2y = v2y / n2
double judge = v1x * v2y - v2x * v1y
double vectorLen = -expand / Math.sqrt((1 - (vv1x * vv2x + vv1y * vv2y)) / 2.0f)
if (judge > 0)
vectorLen *= -1
double vx = vv1x + vv2x
double vy = vv1y + vv2y
vectorLen = vectorLen / norm(vx, vy)
vx *= vectorLen
vy *= vectorLen
ans << new Point(lon: df.call(vx + p.lon), lat: df.call(vy + p.lat))
}
ans
}
/**
* Returns whether a point is within a polygonal area (open interval)
*/
static Boolean isPolygonContainsPoint(List<Point> pts, Point p) {
int nCross = 0
pts.size().times { i ->
//Algorithm idea: take any edge of the polygon, make the horizontal extension line of the point, and solve the number of intersections with the current edge. Here, only the intersection on the right of the solution point is found
def p1 = pts[i], p2 = pts[(i + 1) % pts.size()]
//p1p2 is a horizontal line segment with either no intersections or infinite intersections
if (p1.lat == p2.lat) {
return
}
//point at p1p2 bottom or top -- > no intersection
if (p.lat < [p1.lat, p2.lat].min() || p.lat >= [p1.lat, p2.lat].max()) {
return
}
//Solve the X coordinate of the intersection of the point horizontal line and the current p1p2 edge
double x = p1.lon + (p2.lon - p1.lon) * (p.lat - p1.lat) / (p2.lat - p1.lat)
//Only unilateral intersections are recorded. Here, only the intersections to the right of the points are recorded
if (x > p.lon) {
++nCross
}
}
//The intersection points are odd, and the points are in the polygon; The opposite is the opposite
nCross % 2 == 1
}
/**
* Find the largest inscribed rectangle in the horizontal direction of a polygonal area. Because it is longitude and latitude data, it is accurate to two decimal places, and the error (only small) is about one kilometer
* [Algorithm reference]
* Algorithm flow: https://www.cnblogs.com/naaoveGIS/p/7218634.html
* Maximum rectangle: https://leetcode-cn.com/problems/maximal-rectangle/solution/zui-da-ju-xing-by-leetcode-solution-bjlu/
*
* Algorithm steps:
* 1.The area is segmented according to the minimum circumscribed rectangle. Here, 0.01 is taken as the segmentation point, and the longitude and latitude are segmented every 0.01
* 2.Check whether the area is inside the polygon, Mark 1 for true and 0 for false to obtain the marking matrix
* 3.According to the above marked rectangle, the maximum inscribed matrix is obtained according to the leetcode algorithm. Note that the space complexity is O(mn)
*/
static Rectangle computeLargestEnclosingRectangle(List<Point> pts) {
//1. The area is not really cut into rectangles, but divided into data points, reducing the amount of calculation by 75%
def scale = 0.01
def minimumEnclosingRectangle = computeMinimumEnclosingRectangle(pts)
def regionalSlices = computeRegionalSlices(minimumEnclosingRectangle, scale)
//2. Marking matrix, where the longitude and latitude of the dot matrix are converted into rectangular marking matrix, and each rectangle is marked by the upper left corner,
// For example, the coordinates of the upper left corner of rectangular marks[0][0] are regionalSlices[0][0], and the coordinates of the lower right corner are regionalSlices[1][1]
def marks = computeMarkMatrix(pts, regionalSlices)
//3. Calculate the maximum inscribed matrix and obtain the rectangle
def (minC, maxC, minR, maxR, area) = maximalRectangle(marks)
new Rectangle(minLon: regionalSlices[0][minR].lon, maxLon: regionalSlices[0][maxR + 1].lon,
minLat: regionalSlices[maxC + 1][0].lat, maxLat: regionalSlices[minC][0].lat)
}
/**
* Recursively find the largest rectangle
* The most difficult thing to get here is the shutdown conditions. The roughly calculated shutdown conditions are as follows
*
* Suppose the area of the external rectangle is a1, the area of the internal rectangle is a4, the number of polygon sides is n1, and the number of internal rectangles is n2. It takes time t1 to judge an edge and t2 to judge an internal rectangle,
* When t1 is about three times that of t2, the total time is spent
* t = n2 * a4 / a1 + (n2 + 3 * n1)* (1 - a4 / a1)
* Shutdown conditions:
* If t in this iteration is greater than t in the last iteration, the machine will be shut down and the last data will be taken as the final result
*/
static List<Rectangle> computeLargestEnclosingRectangleRecursion(List<Point> pts) {
//1. The area is not really cut into rectangles, but divided into data points, reducing the amount of calculation by 75%
def scale = 0.01
def minimumEnclosingRectangle = computeMinimumEnclosingRectangle(pts)
def regionalSlices = computeRegionalSlices(minimumEnclosingRectangle, scale)
//2. Marking matrix, where the longitude and latitude of the dot matrix are converted into rectangular marking matrix, and each rectangle is marked by the upper left corner,
// For example, the coordinates of the upper left corner of rectangular marks[0][0] are regionalSlices[0][0], and the coordinates of the lower right corner are regionalSlices[1][1]
def marks = computeMarkMatrix(pts, regionalSlices)
//3. Iterative calculation of optimal solution
def ret = []
//Calculate a1 and n1, which will not change with the number of iterations
def a1 = marks.length * marks[0].length, n1 = pts.size(),
a4 = 0, n2 = 0
def ot, nt = Double.MAX_VALUE
do {
ot = nt
//Calculate a4 and n2, which change with each iteration
def (minC, maxC, minR, maxR, area) = maximalRectangle(marks)
a4 += area
++n2
nt = n2 * a4 / a1 + (n2 + 3.0 * n1) * (1.0 - a4 / a1)
minC.upto(maxC) { i ->
minR.upto(maxR) { j -> marks[i][j] = 0 }
}
ret << new Rectangle(minLon: regionalSlices[0][minR].lon, maxLon: regionalSlices[0][maxR + 1].lon,
minLat: regionalSlices[maxC + 1][0].lat, maxLat: regionalSlices[minC][0].lat)
} while (nt < ot)
ret.removeLast()
ret
}
/**
* Judge whether a point is within a rectangle
*/
static boolean isRectangleContainsPoint(Rectangle rec, Point p) {
return p.lon >= rec.minLon && p.lon <= rec.maxLon
&& p.lat >= rec.minLat && p.lat <= rec.maxLat
}
/**
* Gets the smallest circumscribed rectangle of a polygon area
*/
static Rectangle computeMinimumEnclosingRectangle(List<Point> pts) {
def rec = new Rectangle(
minLon: Double.MAX_VALUE, maxLon: Double.MIN_VALUE,
minLat: Double.MAX_VALUE, maxLat: Double.MIN_VALUE)
pts.each { p ->
rec.minLon = [p.lon, rec.minLon].min()
rec.maxLon = [p.lon, rec.maxLon].max()
rec.minLat = [p.lat, rec.minLat].min()
rec.maxLat = [p.lat, rec.maxLat].max()
}
rec
}
/**
* The number of kilometers needed to expand the province by one kilometer is calculated according to the central point
*/
static def computeExpandDistance(Point p) {
def lon = p.lon, lat = p.lat, scale = 0.0000001
do {
lat += scale
} while (dist(p, new Point(lon: lon, lat: lat)) < 1000.0)
return lat - p.lat
}
/**
* Judge whether the point is in the city
*/
static boolean isCityContainsPoint(ScopeOfCity soc, Point p) {
//Judge the circumscribed rectangle first
if (!isRectangleContainsPoint(soc.minimumEnclosingRectangle, p)) {
return false
}
//Judge inscribed rectangle
soc.regions.find { mp ->
mp.largestEnclosingRectangle.find { rec -> isRectangleContainsPoint(rec, p) }
}.asBoolean() ?:
//Judge polygon
soc.regions.find { mp -> isPolygonContainsPoint(mp.points, p) }.asBoolean()
}
/*---------------------------------------------------------------------------------------------------------------*/
/**
* The lattice of the segmentation matrix is obtained according to the rectangle and the segmentation scale
* In order to reduce the amount of calculation, the output here is not a real rectangle. Because it is equidistant continuous segmentation, the segmented data points can be directly output, with the data points in the upper left corner as the target
*/
private static List<List<Point>> computeRegionalSlices(Rectangle rec, scale) {
//1. Standardize the rectangle according to the segmentation scale
def minLon = floor(rec.minLon, scale), maxLon = ceil(rec.maxLon, scale),
minLat = floor(rec.minLat, scale), maxLat = ceil(rec.maxLat, scale)
//2. Segmentation (due to human habits, it is tentatively divided by line from top to bottom, that is, from large to small according to latitude and from small to large according to longitude)
List<List<Point>> matrix = []
for (def posLat = maxLat; posLat >= minLat; posLat -= scale) {
List<Point> row = []
for (def posLon = minLon; posLon <= maxLon; posLon += scale) {
row << new Point(lon: posLon, lat: posLat)
}
matrix << row
}
matrix
}
/**
* The marking matrix is calculated according to the segmented rectangle and polygon
*/
private static int[][] computeMarkMatrix(List<Point> pts, List<List<Point>> regionalSlices) {
def m = regionalSlices.size(), n = regionalSlices[0].size(),
rectangleMarks = new int[m - 1][n - 1]
//First mark all the rectangular marking matrices as 1, and then mark the matrices not in the polygon as 0 according to the dot matrix calculation
rectangleMarks.each { Arrays.fill(it, 1) }
//Traverse each point of the tangent lattice to obtain the marking matrix
def inRange = { num, min, max -> num >= min && num <= max }
(0..<m).each { posM ->
(0..<n).each { posN ->
def p = regionalSlices[posM][posN]
//Handles points that are not inside a polygon
if (!isPolygonContainsPoint(pts, p)) {
//The point is not inside the polygon. Process the matrix in four directions corresponding to the point. The row range is [0, m-2], and the column range is [0, n-2]
//Upper left corner [posM-1, posN-1]
if (inRange(posM - 1, 0, m - 2) && inRange(posN - 1, 0, n - 2)) {
rectangleMarks[posM - 1][posN - 1] = 0
}
//Upper right corner [posM-1, posN]
if (inRange(posM - 1, 0, m - 2) && inRange(posN, 0, n - 2)) {
rectangleMarks[posM - 1][posN] = 0
}
//Lower left corner [posM, posN1-1]
if (inRange(posM, 0, m - 2) && inRange(posN - 1, 0, n - 2)) {
rectangleMarks[posM][posN - 1] = 0
}
//Lower right corner [posM, posN]
if (inRange(posM, 0, m - 2) && inRange(posN, 0, n - 2)) {
rectangleMarks[posM][posN] = 0
}
}
}
}
rectangleMarks
}
/**
* Find the maximum rectangle according to the marking matrix, and return [minimum row mark maximum row mark minimum column mark maximum column mark maximum area]
*/
static def maximalRectangle(int[][] matrix) {
def m = matrix.length, n = matrix[0].length
int[][] left = new int[m][n]
(0..<m).each { i ->
(0..<n).each { j ->
if (matrix[i][j] == 1) {
left[i][j] = (!j ? 0 : left[i][j - 1]) + 1
}
}
}
def minC = -1, maxC = -1, minR = -1, maxR = -1, ret = 0
(0..<n).each { j -> // For each column, a histogram based approach is used
int[] up = new int[m]
int[] down = new int[m]
Deque<Integer> stack = new LinkedList<>() //Chain stack
for (int i = 0; i < m; i++) {
while (!stack.isEmpty() && left[stack.peek()][j] >= left[i][j]) {
stack.pop()
}
up[i] = stack.isEmpty() ? -1 : stack.peek()
stack.push(i)
}
stack.clear()
for (int i = m - 1; i >= 0; i--) {
while (!stack.isEmpty() && left[stack.peek()][j] >= left[i][j]) {
stack.pop()
}
down[i] = stack.isEmpty() ? m : stack.peek()
stack.push(i)
}
for (int i = 0; i < m; i++) {
int height = down[i] - up[i] - 1
int area = height * left[i][j]
if (area > ret) {
ret = area
minC = up[i] + 1
maxC = down[i] - 1
minR = j - left[i][j] + 1
maxR = j
}
}
}
return [minC, maxC, minR, maxR, ret]
}
private static def ceil(d, scale) {
def n = (1 / scale) as int
(BigDecimal) Math.ceil(d * n) / n
}
private static def floor(d, scale) {
def n = (1 / scale) as int
(BigDecimal) Math.floor(d * n) / n
}
private static def dist(Point p1, Point p2) {
distHarversine(p1.lat, p1.lon, p2.lat, p2.lon)
}
/**
* Here, harverne formula is used to calculate the distance between two longitudes and latitudes (in meters)
*
* @param lat1 Latitude 1
* @param lon1 Longitude 1
* @param lat2 Latitude 2
* @param lon2 Longitude 2
* @return Distance in meters
*/
private static double distHarversine(double lat1, double lon1, double lat2, double lon2) {
double hsinX = Math.sin(Math.toRadians(lon1 - lon2) * 0.5)
double hsinY = Math.sin(Math.toRadians(lat1 - lat2) * 0.5)
double h = hsinY * hsinY + (Math.cos(Math.toRadians(lat1)) * Math.cos(Math.toRadians(lat2)) * hsinX * hsinX)
return 2 * Math.atan2(Math.sqrt(h), Math.sqrt(1 - h)) * 6371001
}
}