As one of the ten classic sorting algorithms, quick sort often appears in the interview field. It requires either handwritten quick sort or a variant of quick sort. In order to facilitate review, quick sort is hereby summarized

1. Fledgling

Given an array arr and a number num, please put the number less than or equal to num on the left of the array and the number greater than num on the right of the array.
Additional space complexity O(1) and time complexity O(N) are required

1. Use rightBound to record the right boundary of the area less than or equal to num, and the initial value is - 1
2. Traverse the array from scratch. If arr[i] < = num, exchange arr[i] with the next number less than or equal to the region, that is, exchange arr[i] with the number with subscript rightBound + 1, and then i++,rightBound + +;
3. If arr [i] > num, only I + +;
   
   code:

public static void test1(int [] arr , int num){
        int rightBound = -1,i = 0;
        while (i <arr.length){
            if(arr[i] <= num) swap(arr,++rightBound,i++);
            else i++;
        }
 }

public static void swap(int [] arr, int i, int j){
     int temp = arr[i];
     arr[i] = arr[j];
     arr[j] = temp;
 }

output:

3 5 4 3 5 7 6 8

2. Test ox knife

Dutch flag issue

Given an array arr and a number num, please put the number less than num on the left of the array, the number equal to num in the middle of the array, and the number greater than num on the right of the array. Additional space complexity O(1) and time complexity O(N) are required

This question is an enhanced version of the previous one

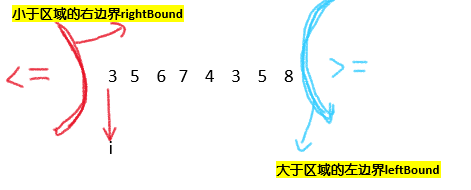
1. Use rightBound to record the right boundary of the area smaller than num, with an initial value of - 1; use leftBound to record the left boundary of the area larger than num, with an initial value of arr.length;
2. Traverse the array from scratch. If arr[i] < num, exchange arr[i] with the next number less than or equal to the region, that is, exchange arr[i] with the number with subscript rightBound + 1, and then i++,rightBound + +;
3. If arr[i] = num, only I + +;
4. arr[i] > num, then exchange arr[i] with the next number greater than the region, that is, exchange arr[i] with the number with the subscript leftBound - 1, and then I stay in place, leftBound –;
5. When i equals leftBound, the loop ends
   (why should I stay in place, because after the exchange of arr[i] and the number with the subscript leftBound - 1, the number corresponding to the I subscript does not know the size and needs to be compared again)

The essence of the solution is to squeeze the number equal to num in the array into the middle by using double pointers

code

	 public static void heLanFlag(int [] arr, int num){
        int rightBound = -1, leftBound = arr.length;
        int i = 0;
        while(i < leftBound){
            if(arr[i] < num) swap(arr,++rightBound,i++);
            else if(arr[i] == num) i++;
            else swap(arr,--leftBound,i);
        }
	 }

	 public static void swap(int [] arr, int i, int j){
	      int temp = arr[i];
	      arr[i] = arr[j];
	      arr[j] = temp;
     }

output:

3 3 4 5 5 7 8 6

3. Perfect (fast discharge)

Using the Dutch flag for zoning, it is divided into 3 areas (<, =, >) and the score is 2 areas (< = and >)

The worst-case complexity of this algorithm is O(n2)
because
1,4,3,5,7,6,8,9 in this case, perform fast scheduling, and divide the last number of the array each time. After division, there is no area larger than the area on the right, that is, only the current number is fixed. The worst time complexity is O(n2)

code

	public static void quickSort(int[] arr) {
        if (arr == null || arr.length < 2) {
            return;
        }
        quickSort(arr, 0, arr.length - 1);
    }

    public static void quickSort(int[] arr, int l, int r) {
        if (l < r) {
        	//int[] p has a capacity of 2 and returns the left and right boundaries equal to the region
            int[] p = partition(arr, l, r);
            quickSort(arr, l, p[0] - 1);
            quickSort(arr, p[1] + 1, r);
        }
    }

    public static int[] partition(int[] arr, int l, int r) {
        int rightBound = l - 1;
        int leftBound = r;
        while (l < leftBound) {
            if (arr[l] < arr[r]) {
                swap(arr, ++rightBound, l++);
            } else if (arr[l] > arr[r]) {
                swap(arr, --leftBound, l);
            } else {
                l++;
            }
        }
        swap(arr, leftBound, r);
        //Returns the left and right boundaries of equal values
        return new int[] { rightBound + 1, leftBound };
    }

    public static void swap(int[] arr, int i, int j) {
        int tmp = arr[i];
        arr[i] = arr[j];
        arr[j] = tmp;
    }

4. Reach the peak (random quick row)

In the above quick sorting, the last array in the region is divided according to the Dutch flag every time (called partition here). Therefore, if the data status is 1,4,3,5,7,6,8,9, take 9 and divide it, and there are only two regions after dividing the region, the time complexity will reach O(n2);

Therefore, the improved version of quick sort is based on the idea of randomization
Select a number from the array with medium probability to exchange with the last number of the region, and then partition according to the last number of the array after exchange, so that the good and bad cases are equal probability!!

Dimensionality only needs to select a number randomly on the basis of the former

public static double random()
Returns a double with a positive sign, greater than or equal to 0.0 and less than 1.0. The returned values are pseudo randomly selected from a range (approximately) evenly distributed.

public static void quickSort(int[] arr) {
       if (arr == null || arr.length < 2) {
           return;
       }
       quickSort(arr, 0, arr.length - 1);
   }

   public static void quickSort(int[] arr, int l, int r) {
       if (l < r) {
           //Math.random() returns a double greater than or equal to 0.0 and less than 1.0.
           swap(arr, l + (int) (Math.random() * (r - l + 1)), r);
           int[] p = partition(arr, l, r);
           quickSort(arr, l, p[0] - 1);
           quickSort(arr, p[1] + 1, r);
       }
   }

   public static int[] partition(int[] arr, int l, int r) {
       int rightBound = l - 1;
       int leftBound = r;
       while (l < leftBound) {
           if (arr[l] < arr[r]) {
               swap(arr, ++rightBound, l++);
           } else if (arr[l] > arr[r]) {
               swap(arr, --leftBound, l);
           } else {
               l++;
           }
       }
       swap(arr, leftBound, r);
       //Returns the left and right boundaries of equal values
       return new int[] { rightBound + 1, leftBound };
   }

   public static void swap(int[] arr, int i, int j) {
       int tmp = arr[i];
       arr[i] = arr[j];
       arr[j] = tmp;
   }

It is obtained according to Master formula and through probability accumulation calculation (it needs to be proved by mathematical derivation)
Time complexity analysis O(N*logN)
Spatial complexity analysis O(logN)