After adjusting the trees for a long time, they finally became gorgeous
Main idea of the title:
Given a tree structure, point 1 is the root of the tree The closer to the tree root, the higher the temperature. The existing survival temperature is in the [L,R] range. The virus appears at point X. if the temperature of a node is in the [L,R] range and its adjacent point is infected with the virus, the point will also be infected with the virus
There are many inquiries. Each time, ask how many points can be infected by a virus with survival temperature [L,R] at point X
Think about violence first: violence dfs is bound to TLE
Considering the tree structure given in the title and the monotonicity of temperature growth, the process of virus infection can be divided into two steps: first, starting from the current point, find the point whose temperature is less than or equal to R and closest to the source point (find the ancestor), and then infect downward from this point. All the temperature intervals in the infected subtree are at [L,R]
The first step is to find ancestors by multiplying

=======begin
(those who know the multiplication method can skip this part)
Principle of multiplication:
If you want to jump just 60 meters in the long jump competition, you can jump many times, and you can only jump the following distances: 1,2,4,8,16,32,64128 meters
First try to jump with 128 meters, obviously not, it will exceed 60 meters. Now, change to jump with 64 meters, but not, so it is feasible to use 32 meters. At this time, your position is 32 meters, there are 28 meters from 60 meters, then jump with 16 meters, it is feasible, there are 12 meters, then jump with 8 meters, it is feasible, there are still 4 meters, and then jump with 4 meters, you can just jump to 60 meters
This is the principle of multiplication
How to construct a multiplier array:
Let an array int up [n] [30], up [i] [J] represent the number of points reached after traversing 2^j nodes upward from point I
Where up[i][0] represents the number of the point reached when point I moves 2 ^ 0 = 1 points upward, that is, its parent node
Suppose point j is the parent node of point i and up[j][0]=k, that is, K is the parent node of y
Then k is the grandfather node of i
up[i][1] represents the position reached by I moving up 2 ^ 1 nodes, that is, its grandfather node K
At the same time, point i moves up two points to reach K, which is equivalent to its parent node moving up one point to reach K
That is, up[i][1]=up [parent node] [0]
That is, up [i] [J] = up [up [i] [J - 1] [J - 1];
This idea is similar to DP, and the complete derivation code is:

for (int j = 1; j <= 20; j++) { 
		for (int i = 1; i <= n; i++) {
			up[i][j] = up[up[i][j - 1]][j - 1];
		}
	}

In this way, we can quickly build the point i reached after jumping 2^j points
In this topic: how to quickly find the point with the highest temperature and closest to the source point in the main line of point X
Let's try to jump from far to near, let i=20, if we jump for the first time
: the temperature [up [x] [i]] > R indicates that this step is a long jump. Let i-1 and continue to try to jump
When a certain temperature [up [x] [i]] < = R indicates that it can be skipped, let x = up[x][i];
However, one jump is not complete. Continue to try to jump after i-1 until I < 0
code:

for (int i = 20; i >= 0; i--) { 
			if (t[up[x][i]] <= r)
				x = up[x][i];
		}

===========end
The next step is to see how many points r > = temperature > = L are under the subtree of this ancestor node

============begin

(if you know what the chairman tree is, you can skip this part)
Chairman tree = = persistent segment tree
First of all, this is a lovely ordinary line segment tree

When we modify one of the points, but want to keep the information before modification, if the method is to create a new line segment tree, copy the information of other points one by one except the modified points
(the black point is the modified point)

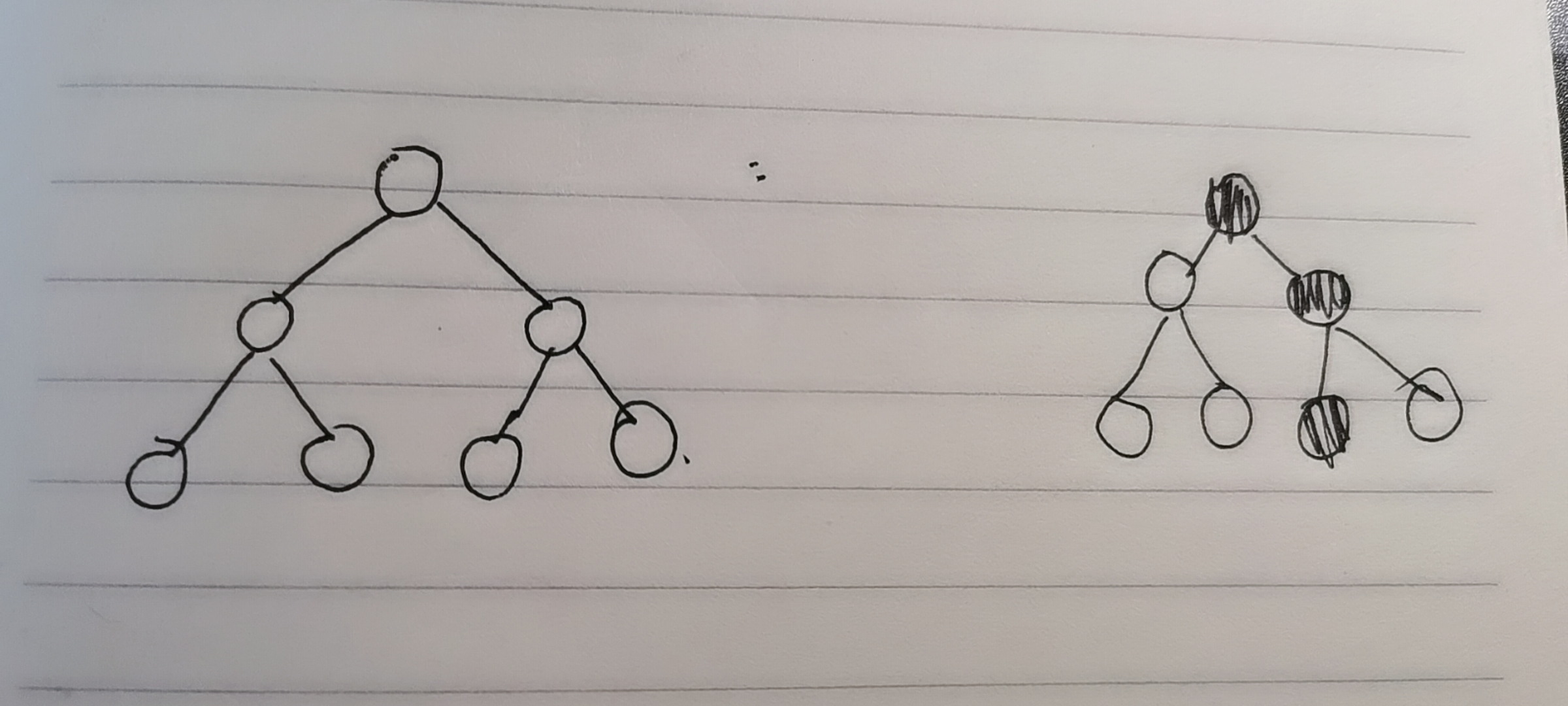
However, this is very space consuming, so we consider only creating new points that will be modified

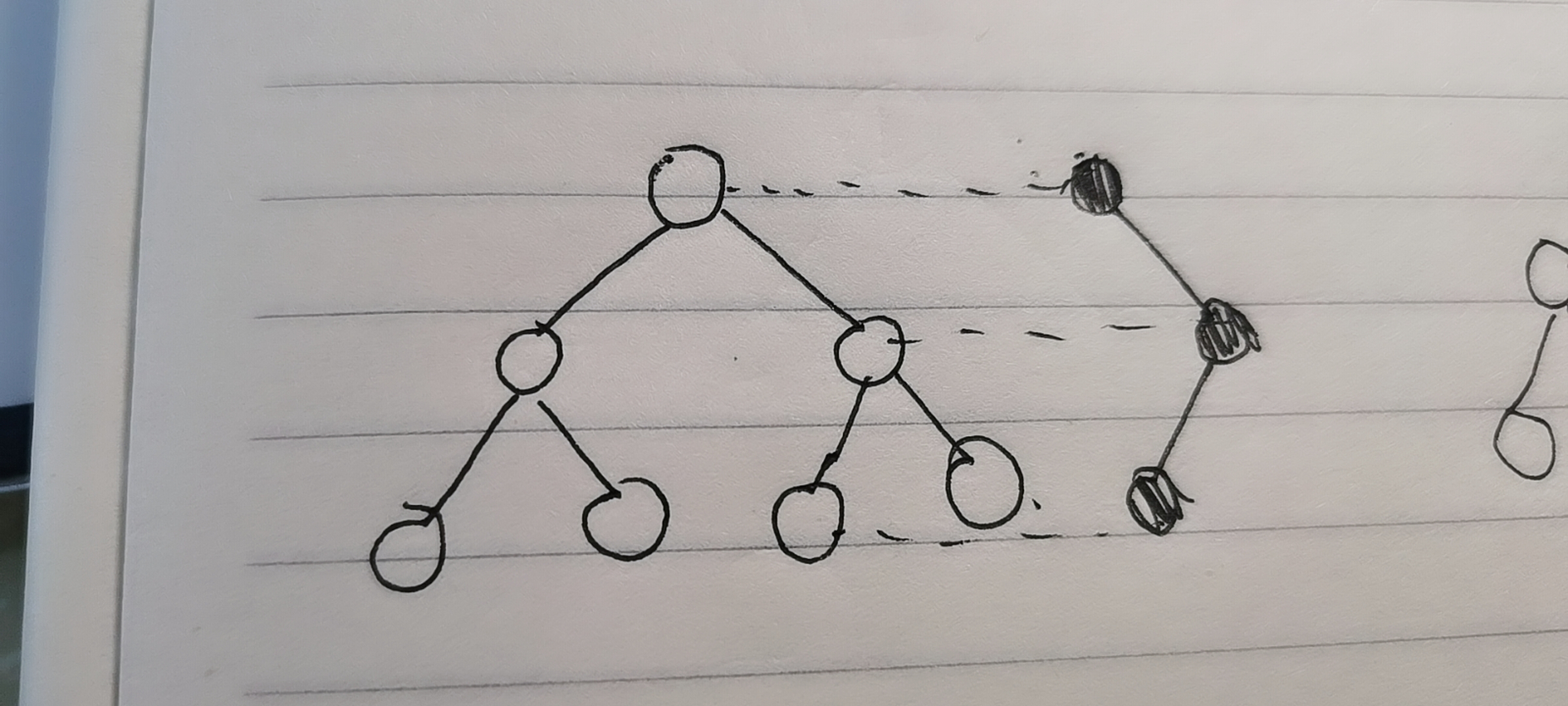
The unmodified subtree of these new nodes points to the original segment tree

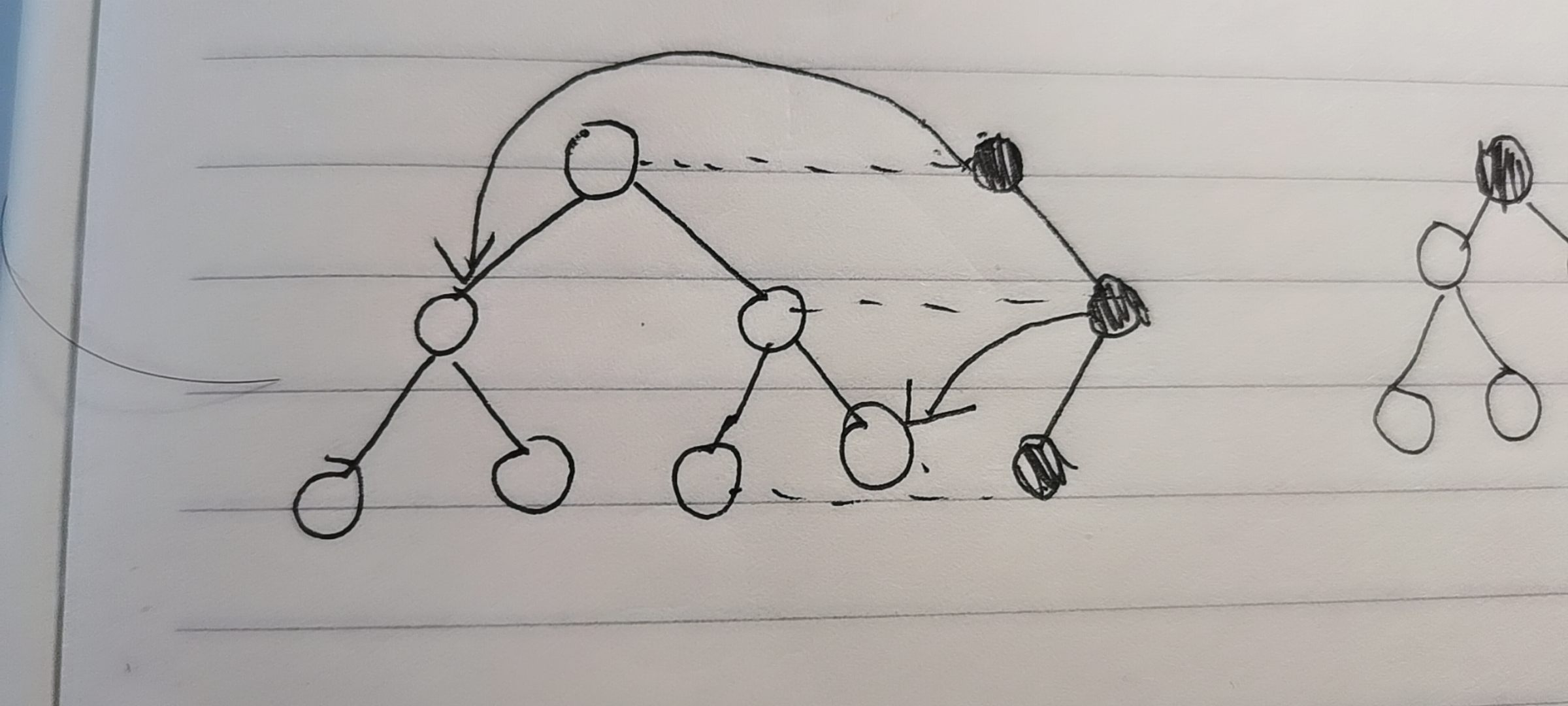
In this way, as long as the root number of each new tree is recorded in root[N], each version of segment tree can be obtained

=========end

===================begin

(you can skip this part if you know the dfs sequence to build the chairman tree)
First, if you want to know which points are in the subtree of this ancestor node, you can use dfs to traverse the whole tree and record the time stamps of recursive entry (in) and exit (out)

void dfs(int u, int f) {
	fa[u] = f;
	in[u] = ++idx;
	ord[idx] = u;
	for (int i : g[u]) {
		if (i != f)
			dfs(i, u);
	}
	out[u] = idx;
}

After the recursion is completed, the in and out of each point

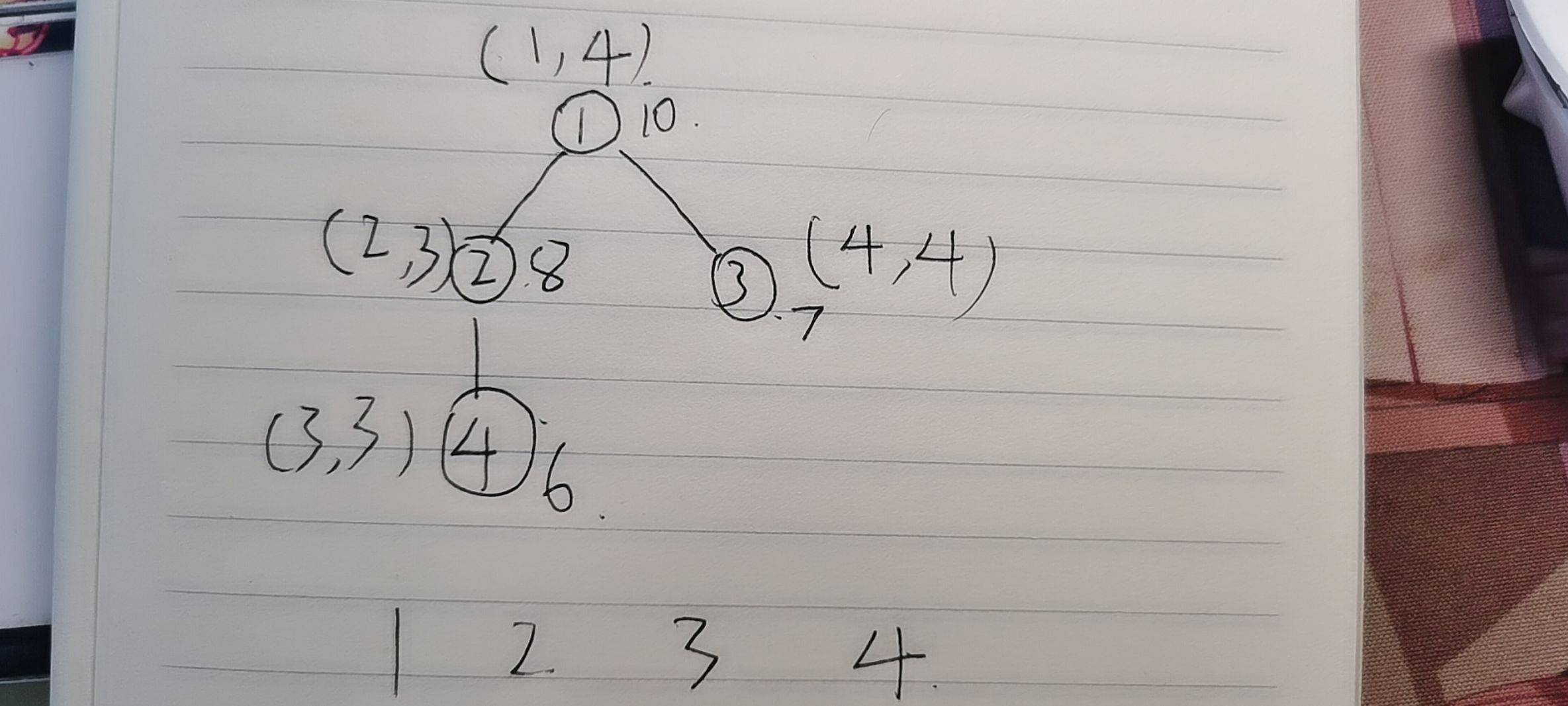
(the first number in the number pair is in and the second number is out)
For example, find the child node of point 2, whose in is 2 and out is 3. The areas with subscripts 2 and 3 are covered in 1, 2, 3 and 4. The number in this area is the number of its child nodes

========================end

We can maintain a chairman tree, and maintain the number of nodes between temperature L and R in each version
However, there are two intervals during query, one is the current subtree interval and the other is the temperature interval [L,R]
Therefore, we can use the idea of class prefix sum to build the chairman tree in dfs sequence, then ask the number of points in the temperature interval [L,R] in the root[out[x]] Version (the version that has added the subtree of point x), and then ask the number of points in the temperature interval [L,R] in the root[in[x]-1] Version (the version that has not started adding point X and its subtree) Subtracting the two is the point in [L,R] of the temperature interval under the X subtree
Complete code

#include <bits/stdc++.h>
using namespace std;
const int N = 100010; //point
vector<int>g[N];
int t[N];//temperature
int fa[N];
int up[N][30];//Multiplier array
int in[N], out[N]; //Record the dfs sequence at the time of entry and exit
int ord[N];//Record the points corresponding to the in array in the dfs sequence
int idx;

void dfs(int u, int f) {
	fa[u] = f;
	in[u] = ++idx;
	ord[idx] = u;
	for (int i : g[u]) {
		if (i != f)
			dfs(i, u);
	}
	out[u] = idx;
}

struct node { //Chairman tree node
	int val;//Maintenance node
	int l, r; //Number of left and right sons
} a[20001000];

int root[N];//Record version
int tot;//Number of versions
//           Temperature position where the insertion is performed in the temperature area of the new version and the old version
void modify(int x, int f, int l, int r, int pos) {
	if (l == r) {
		a[x].val = a[f].val + 1;
		return ;
	}
	int mid = l + r >> 1;
	if (pos <= mid) {
		a[x].r = a[f].r; //The modification interval is on the left and will not affect the right son of the previous version
		a[x].l = ++tot; //New point
		modify(a[x].l, a[f].l, l, mid, pos);
	} else {
		a[x].l = a[f].l;
		a[x].r = ++tot;
		modify(a[x].r, a[f].r, mid + 1, r, pos);
	}
	a[x].val = a[a[x].l].val + a[a[x].r].val;

}
//                   Current interval query interval
int query(int x, int l, int r, int ll, int rr) {
	if (x == 0)
		return 0;
	if (l >= ll && r <= rr)
		return a[x].val;
	if (l > rr || r < ll)
		return 0;
	int mid = l + r >> 1;
	return query(a[x].l, l, mid, ll, rr) + query(a[x].r, mid + 1, r, ll, rr);
}


int main() {
	ios::sync_with_stdio(false);
	int n;
	cin >> n;
	for (int i = 1; i < n; i++) {
		int u, v;
		cin >> u >> v;
		g[u].push_back(v);
		g[v].push_back(u);
	}
	for (int i = 1; i <= n; i++)
		cin >> t[i];
	t[0] = 1e9+10;
	dfs(1, 0); 
	
	
	for (int i = 1; i <= n; i++)
		up[i][0] = fa[i]; //Skip 2 ^ 0 times is its parent node
	for (int j = 1; j <= 20; j++) { //Build a multiplier array (used to quickly find ancestors whose temperature reaches the limit)
		for (int i = 1; i <= n; i++) {
			up[i][j] = up[up[i][j - 1]][j - 1];
		}
	}
	for (int i = 1; i <= n; i++) {
		root[i] = ++tot;
		//     The temperature limits of the new version and the old version build the chairman tree in the order of dfs
		modify(root[i], root[i - 1], 1, 1e9, t[ord[i]]);
	}
	int q;
	cin >> q;
	while (q--) {
		int x, l, r;
		cin >> x >> l >> r;
		if (t[x] < l || t[x] > r) {
			cout << "0" << endl;
			continue;
		}

		for (int i = 20; i >= 0; i--) { //Double looking for ancestors
			if (t[up[x][i]] <= r)
				x = up[x][i];
		}					
		cout << query(root[out[x]], 1, 1e9, l, r) - query(root[in[x] - 1], 1, 1e9, l, r) << endl;             
	}

	return 0;
}