This article will summarize some tensor operations commonly used by Pytorch and explain their functions, and then use these operations to realize the algorithms of normalization operations, such as BN,GN,LN,IN, etc!

Common tensor operations

cat

When the data is spliced along a certain dimension, the total dimension after cat remains unchanged. It should be noted that the dimension of a certain dimension should be the same when the two tensors are cat, otherwise an error will be reported!

import torch
x = torch.randn(2,3)
y = torch.randn(1,3)
torch.cat((x, y), 0)   # Dimension is (3, 3)
z = torch.randn(1, 4)
torch.cat((x, z), 0)  # report errors

stack

Compared with Cat, Stack will add new dimensions and Stack the two matrices on the new dimensions. Generally, the dimensions of the two matrices are the same!

import torch
x = torch.randn(1,2)
y = torch.randn(1,2)
torch.stack((x, y), 0)   # Stack in the 0 dimension with dimensions (2, 1, 2)
torch.stack((x, y), 1)   # Dimension is (1, 2, 2)

transpose

Its function is to exchange two dimensions, similar to the transpose of two-dimensional matrix!

import torch
x = torch.randn(2,3)
x.transpose(0, 1)  # Dimension is (3, 2)

permute

It is equivalent to the enhanced version of transfer, which is suitable for multidimensional data and more flexible!

import torch
x = torch.randn(1,2,3,4)
x_p = x.permute(1,0,2,3)  # Dimension becomes (2,1,3,4)

squeeze and unsqueeze

squeeze(dim) means to compress, that is, remove dim with dimension number of 1. By default, all dim with dimension number of 1 are removed. Of course, you can also specify it yourself, but if the specified dimension number is not 1, no change will occur. unsqueeze(dim) is the opposite of squeeze(dim), which is used to add a dimension.

import torch
x = torch.randn(2,1)
x.squeeze()   # Dimension (2,)
x.squeeze(1)  # Dimension (2,)
x.unsqueeze(2) # Dimension (2,1,1)
x.unsqueeze(0) # Dimension (1,2,1)

view, continuous, and reshape

Some tensors do not occupy a whole block of memory, but are composed of different data blocks. The view() operation of tensor depends on the fact that the memory is a whole block. At this time, only the function continuous () needs to be executed to turn the tensor into a form of continuous distribution in memory. Especially in pytorch0 In 4, after using permute and transfer, the memory is discontinuous, so you can't use the view function directly. You should first change continuous () into continuous memory, and then use view.
Pytorch0. In 4, a reshape function is added, which is equivalent to continuous() View() function!

Implementation of normalization algorithm

Today, we will only consider how to implement it. As for the principle of normalization, we won't repeat it. We have written a lot in Zhihu and blog. For these normalization methods, such as BN (batch), ln (layer), in (instance) and GN (Group), there is a diagram in GN's paper that can be clearly described. We don't need to look at the formula, just remember the following diagram! (the blue area is the normalized area. In other words, the mean and variance used in each normalization are calculated from the blue area, and then applied to the blue area for normalization).

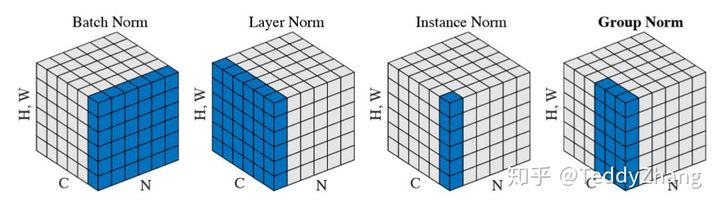
Normalized diagram

Then we can look at the simple implementation (normalization only)

Batch Normalization

import torch
from torch import nn
bn = nn.BatchNorm2d(num_features=3, eps=0, affine=False, track_running_stats=False)
x = torch.rand(10, 3, 5, 5)*10000
official_bn = bn(x)   # Official code

x1 = x.permute(1, 0, 2, 3).reshape(3, -1) # Calculate the mean variance for (N, H, W)
mean = x1.mean(dim=1).reshape(1, 3, 1, 1)
# x1. Dimension after mean (dim = 1) is (3,)
std = x1.std(dim=1, unbiased=False).reshape(1, 3, 1, 1)
my_bn = (x - mean)/std
print((official_bn-my_bn).sum())  # output error 

Layer Normalization

import torch
from torch import nn
ln = nn.LayerNorm(normalized_shape=[3, 5, 5], eps=0, elementwise_affine=False)
x = torch.rand(10, 3, 5, 5)*10000
official_ln = ln(x)   # Official code

x1 = x.reshape(10, -1)  # Calculate the mean variance for (C,H,W)
mean = x1.mean(dim=1).reshape(10, 1, 1, 1)
std = x1.std(dim=1, unbiased=False).reshape(10, 1, 1, 1)
my_ln = (x - mean)/std
print((official_ln-my_ln).sum())

Instance Normalization

import torch
from torch import nn
In = nn.InstanceNorm2d(num_features=3, eps=0, affine=False, track_running_stats=False)
x = torch.rand(10, 3, 5, 5)*10000
official_In = In(x)   # Official code

x1 = x.reshape(30, -1)  # Calculate the mean variance for (H,W)
mean = x1.mean(dim=1).reshape(10, 3, 1, 1)
std = x1.std(dim=1, unbiased=False).reshape(10, 3, 1, 1)
my_In = (x - mean)/std
print((official_In-my_In).sum())

Group Normalization

import torch
from torch import nn
gn = nn.GroupNorm(num_groups=4, num_channels=20, eps=0, affine=False)
# Divided into 4 groups, that is, the blue area is (5, 5, 5)
x = torch.rand(10, 20, 5, 5)*10000
official_gn = gn(x)   # Official code

x1 = x.reshape(10,4,-1)  # Calculate the mean variance for (H,W)
mean = x1.mean(dim=2).reshape(10, 4, -1)
std = x1.std(dim=2, unbiased=False).reshape(10, 4, -1)
my_gn = ((x1 - mean)/std).reshape(10, 20, 5, 5)
print((official_gn-my_gn).sum())

The above code refers to and modifies the self-knowledge article( https://zhuanlan.zhihu.com/p/69659844)

Source link: https://zhuanlan.zhihu.com/p/76255917