⭐ Write in front
- This is the way to learn the source code of Wenwen al
- 👍 If it helps you, give the blogger a free praise to encourage QAQ
- 👋 Blog home page 🎉 Winwin El learning house
- ⭐ More articles 👨🎓 Stay tuned to wenwendell's home page
- 🍅 Article release date: December 2021 sixteen
- 👋 java learning road!
- 🔎 For more articles, please pay attention to the personal home page!
- 🔎 List of popular articles:
- 🍅 [source code] super detailed ArrayList underlying source code + classic interview questions
- 🍅 HashMap underlying red black tree principle (super detailed diagram) + handwritten red black tree code
- 🍅 HashMap underlying source code analysis (super detailed illustration + interview questions)
- 🍅 HashMap underlying source code analysis (super detailed illustration)

⭐ ﹥ 1 inheritance system diagram of LinkedList
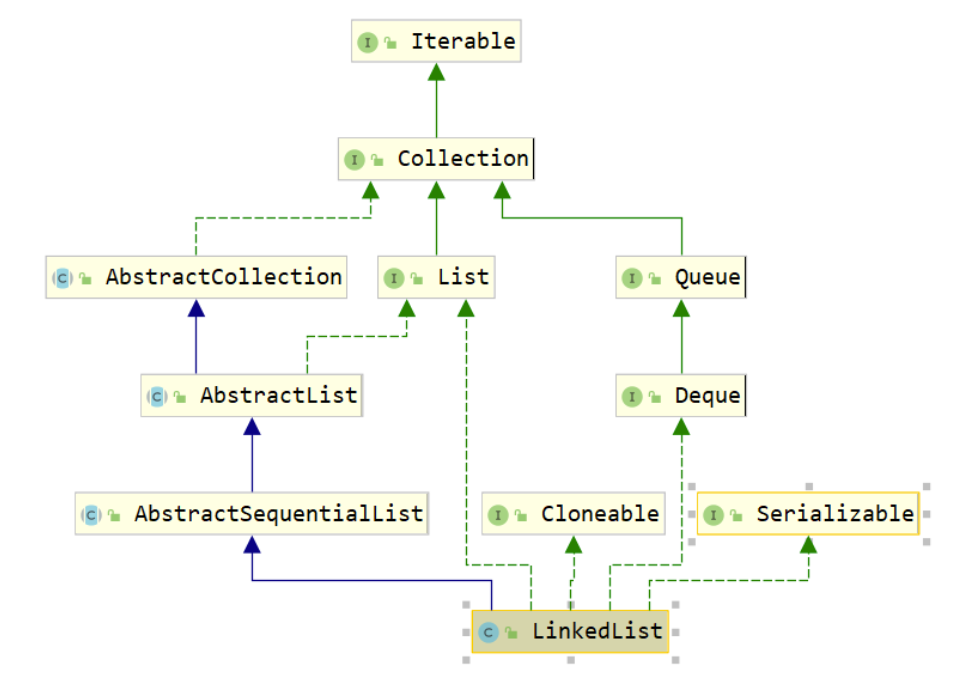
You can see from the inheritance system - LinkedList Realized Queue and Deque Interface, so it can be used as List It can also be used as a double ended queue, or even as a - Stack to use - LinkedList Realized Cloneable and Serializable Interface, from which LinkedList Can be cloned and serialized
⭐ ⅸ 2 LinkedList source code analysis
⭐ ⒋ 2.1 main properties of LinkedList
//size: the number of elements in the linked list transient int size = 0; //first: the head node in the linked list transient Node<E> first; //Last: the last node in the linked list transient Node<E> last;
transient:
Add the keyword transient before the attribute that does not need to be serialized. When serializing an object, this attribute will not be serialized to the specified destination
Therefore, size, first and last will not be serialized

⭐ 2.2 LinkedList source code
⭐ ️2.2. 1. LinkedList construction method
Nonparametric structure
public LinkedList() {
}
Parametric structure
//Pass in the Collection collection and add the elements in the Collection collection to the LinkedList Collection
public LinkedList(Collection<? extends E> c) {
this();
addAll(c);
}
public boolean addAll(Collection<? extends E> c) {
return addAll(size, c);
}
public boolean addAll(int index, Collection<? extends E> c) {
//Check whether the index is out of bounds
checkPositionIndex(index);
//Convert collection to Object [] array
Object[] a = c.toArray();
//Get the length of the array and record it as numNew
int numNew = a.length;
//If the array length is 0, it proves that there are no elements to add
if (numNew == 0)
return false;
//pred is the precursor node pointer of the set to be spliced, and succ is the successor node pointer of the set to be spliced
Node<E> pred, succ;
//If the index of the position to be inserted is at the end of the linked list
if (index == size) {
//The successor of set c is empty
succ = null;
//The precursor of set c is the tail node of the original linked list
pred = last;
} else {
//node(index) is the node at the index. The successor of the collection to be inserted points to it
succ = node(index);
//The predecessor node of the collection to be inserted points to the previous node of the node where index is located
pred = succ.prev;
}
//Start insertion
for (Object o : a) {
@SuppressWarnings("unchecked") E e = (E) o;
//Create a new node. The precursor of the new node points to the precursor of the node where index is located
Node<E> newNode = new Node<>(pred, e, null);
//If it is empty, it proves that the node to be inserted is at the head of the linked list
if (pred == null)
//The first pointer points to the new node
first = newNode;
else
//Otherwise, the successor of pred points to the new node
pred.next = newNode;
//pred move backward
pred = newNode;
}
//If succ==null, it means that index is at the end of the linked list. Add a collection directly at the end
if (succ == null) {
//The tail pointer points to the tail of the spliced linked list
last = pred;
} else {
//Otherwise, the successor to the tail of the set to be inserted is succ
pred.next = succ;
//The precursor of succ points to the tail of the insertion set
succ.prev = pred;
}
//Linked list capacity + length of set to be inserted
size += numNew;
//Linked list modification times + 1
modCount++;
return true;
}
⭐ ️2.2. 2 method of adding elements
As a double ended queue, LinkedList can add elements from the head of the queue or from the tail of the queue
⭐ Add element at the head of the team
public void addFirst(E e) {
//Call the linkFirst method and insert the e element into the linkedlist header
linkFirst(e);
}
private void linkFirst(E e) {
//f record the first node of the queue
final Node<E> f = first;
//Create a new node so that the next of the new node is the first node of the original queue, and the prev of the new node is empty
final Node<E> newNode = new Node<>(null, e, f);
//The new node is the new first node, and the first pointer points to the new node
first = newNode;
//Determine whether the linked list is empty
//If NULL, the tail pointer last points to the new node
//Otherwise, point the prev of the original queue head node to the new node
if (f == null)
last = newNode;
else
f.prev = newNode;
//Linked list capacity + 1
size++;
//The number of times the linked list is modified + 1, indicating that this is a set that supports fail fast
modCount++;
}
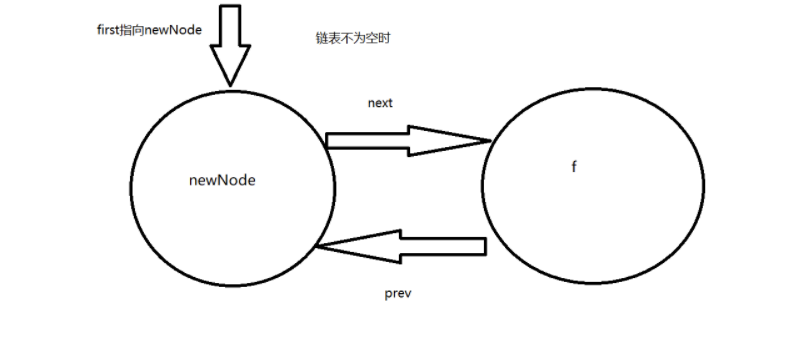
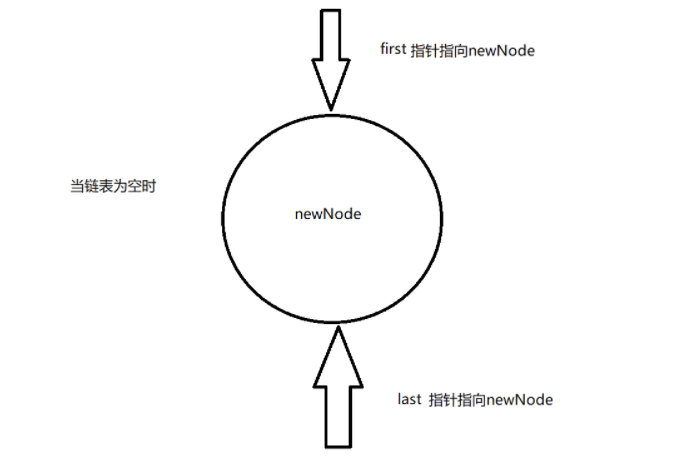

⭐ Add elements at the end of the queue
public void addLast(E e) {
//Call the linkLast method and insert the e element at the end of linkedlist
linkLast(e);
}
void linkLast(E e) {
//l record queue tail node
final Node<E> l = last;
//Create a new node. The prev of the new node is the end of the original queue, and the next of the new node is empty
final Node<E> newNode = new Node<>(l, e, null);
//The new node is the new tail node, and the tail pointer points to the new node
last = newNode;
//Determine whether there are element nodes in the linked list
//If empty, the new node is the first element of the queue
//Then the header pointer also points to the new node
if (l == null)
first = newNode;
else
//If the linked list is not empty, the next of the original last node points to the new node to add the new node to the linked list
l.next = newNode;
//Linked list capacity + 1
size++;
//The number of times the linked list is modified + 1, indicating that this is a set that supports fail fast
modCount++;
}
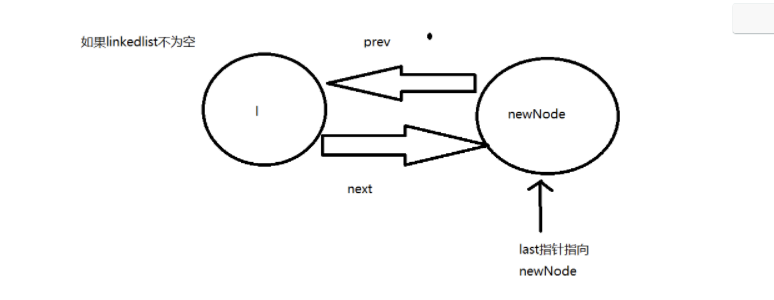
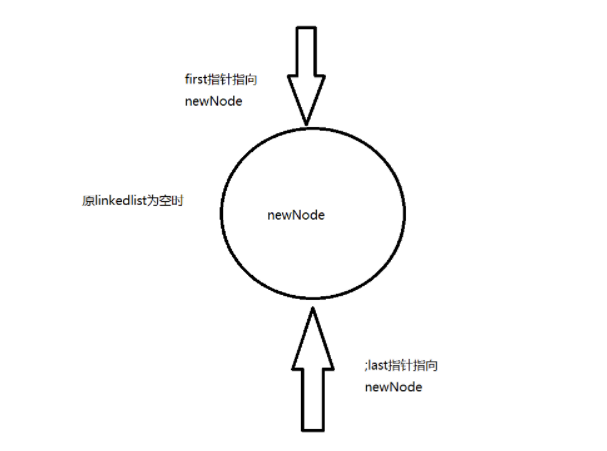
⭐ ﹥ add an element at the specified element location
public void add(int index, E element) {
//Check whether the index is out of bounds
checkPositionIndex(index);
//Determine whether the index is the tail position
if (index == size)
//If the index is the tail position, insert it directly after the tail node
linkLast(element);
else
//Otherwise, in the middle position, call linkBefore to insert the node in the middle position
//node(index) is the node at the current insertion location
linkBefore(element, node(index));
}
//Find the Node at the index location according to the index
Node<E> node(int index) {
//Size > > 1 = size / 2. If index < size / 2, it proves that the node is in the first half of the linked list
if (index < (size >> 1)) {
//Locate the position of the index element from the beginning node
Node<E> x = first;
for (int i = 0; i < index; i++)
x = x.next;//The pointer moves backward until the index is reached
return x;//When the index position is reached, the node node of the position is returned
} else {
//Otherwise, start looking for the index element from the tail node
Node<E> x = last;
for (int i = size - 1; i > index; i--)
x = x.prev;//Before reaching the index, the pointer moves forward
return x;//When the index position is reached, the node node of the position is returned
}
}
//e is the node to be inserted, and succ is the original location node
void linkBefore(E e, Node<E> succ) {
//Find the previous node of the original location node and mark it as pred
final Node<E> pred = succ.prev;
//Create a new node according to e, the prev of the new node is the previous node of the original location node, and the next of the new node is the original location node
final Node<E> newNode = new Node<>(pred, e, succ);
//The leading pointer prev of the original node points to the new node
succ.prev = newNode;
//If succ is the first element of the linked list
if (pred == null)
//Then the first pointer points to the new node, which is the chain header node
first = newNode;
else
//Otherwise, the next of pred is a new node
pred.next = newNode;
//Linked list capacity + 1
size++;
//Linked list modified times + 1
modCount++;
}

⭐ illustration of three ways to add elements
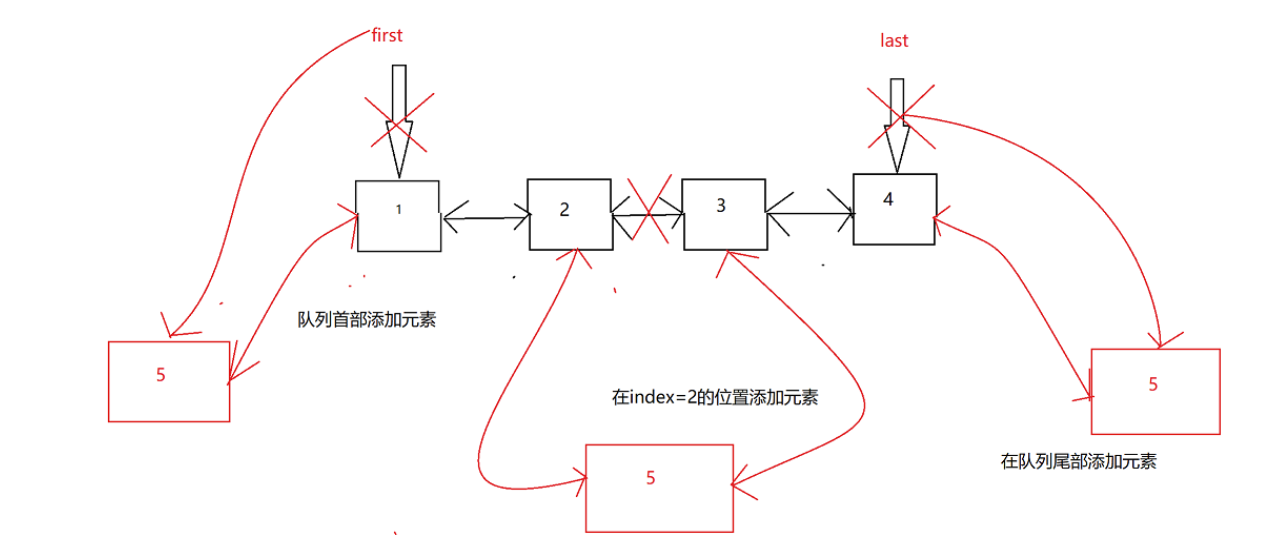
You can see that adding elements at the beginning and end of the queue is very efficient, and the time complexity is O(1)
Adding elements in the middle is inefficient. You need to find the node at the insertion position first, and then modify the front and rear pointers. The time complexity is O(n)
⭐ ️2.2. 3 delete element
As mentioned above, LinkedList implements the Queue and Deque interfaces, so it can be used as a List or as a double ended Queue. As a double ended Queue, it can delete elements from the head of the Queue or from the tail of the Queue. As a List, it can also delete elements from the middle
⭐ ﹥ delete element from header
public E removeFirst() {
//Get first node
final Node<E> f = first;
//If the first node is empty, the linked list is empty and a NoSuchElementException() exception is thrown
if (f == null)
throw new NoSuchElementException();
//Otherwise, delete the header element
return unlinkFirst(f);
}
private E unlinkFirst(Node<E> f) {
// assert f == first && f != null;
//Gets the value of the header node, which is used to return
final E element = f.item;
//Obtain the successor node of the first node
final Node<E> next = f.next;
//Set the value of the first node to null
f.item = null;
//Empty the successor of the first node
f.next = null; // The purpose of empty is to facilitate GC garbage collection
//Take the successor of the first node as the new first node
first = next;
//If the linked list is empty after deletion
if (next == null)
//Set last to null
last = null;
else
//Set the precursor of next to null
next.prev = null;
//Capacity of linked list - 1
size--;
//Modification times of linked list + 1
modCount++;
//Returns the deleted element
return element;
}
⭐ Delete element from tail
public E removeLast() {
//Get tail node
final Node<E> l = last;
//If the linked list is empty, an exception is thrown
if (l == null)
throw new NoSuchElementException();
//Otherwise, delete the tail element
return unlinkLast(l);
}
private E unlinkLast(Node<E> l) {
//Gets the value of the tail node
final E element = l.item;
//Get the precursor of the tail node
final Node<E> prev = l.prev;
//Set the value of the tail node to null
l.item = null;
//Leave the precursor of the tail node empty
l.prev = null; //garbage collection
//The precursor of the tail node is used as the new tail node
last = prev;
//If the precursor of the tail node is empty, the linked list is empty and first is empty
if (prev == null)
first = null;
else
//Otherwise, the successor of prev is set to null
prev.next = null;
//Capacity of linked list - 1
size--;
//Number of times the linked list has been modified + 1
modCount++;
//Return the deleted tail node
return element;
}
⭐ Delete the specified subscript node
public E remove(int index) {
//Check whether the index is out of bounds. If it is out of bounds, an IndexOutOfBoundsException exception will be thrown
checkElementIndex(index);
//node(index) is the node to be deleted
return unlink(node(index));
}
//Find the Node at the index location according to the index
Node<E> node(int index) {
//Size > > 1 = size / 2. If index < size / 2, it proves that the node is in the first half of the linked list
if (index < (size >> 1)) {
//Locate the position of the index element from the beginning node
Node<E> x = first;
for (int i = 0; i < index; i++)
x = x.next;//The pointer moves backward until the index is reached
return x;//When the index position is reached, the node node of the position is returned
} else {
//Otherwise, start looking for the index element from the tail node
Node<E> x = last;
for (int i = size - 1; i > index; i--)
x = x.prev;//Before reaching the index, the pointer moves forward
return x;//When the index position is reached, the node node of the position is returned
}
}
E unlink(Node<E> x) {
//Get the value of the node (x) to delete
final E element = x.item;
//Obtain the successor node of x
final Node<E> next = x.next;
//Get the precursor node of x
final Node<E> prev = x.prev;
//If the precursor is empty, x is the first node, and the successor of x is the new first node
if (prev == null) {
first = next;
} else {
//Then the next of the precursor points to the successor of x
prev.next = next;
//Empty the front drive of x
x.prev = null;
}
//If the successor is empty, x is the tail node, and the precursor of x is the new tail node
if (next == null) {
last = prev;
} else {
//Otherwise, point the subsequent prev to the precursor of x
next.prev = prev;
//The successor of x is set to null
x.next = null;
}
//After the above two steps, the predecessor and successor of x are empty. Set the value of x to empty for GC garbage collection
x.item = null;
//Capacity of linked list - 1
size--;
//Number of times the linked list has been modified + 1
modCount++;
//Returns the deleted element
return element;
}
⭐ Illustration of three methods to delete elements
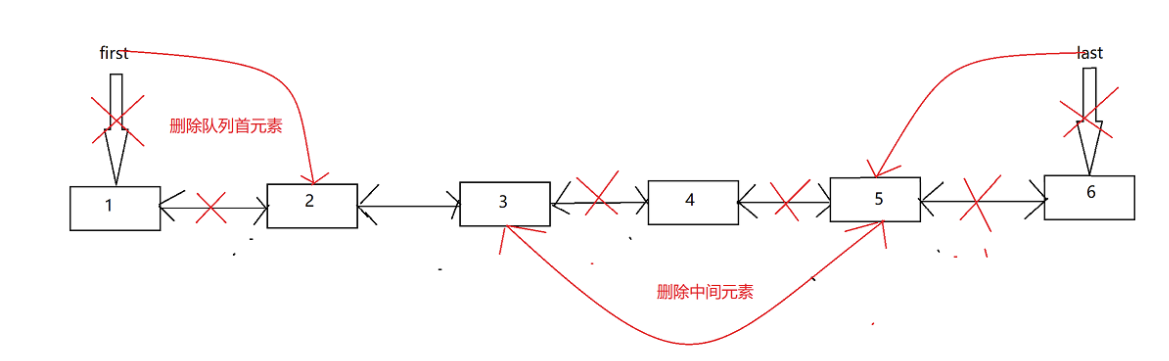
From this we can know
- When deleting elements, it is efficient to delete elements at the beginning and end of the queue, and the time complexity is O(1)
- It is inefficient to delete elements in the middle. First, stand at the node where they are deleted, and then modify the front and back pointers. The time complexity is O(n)
⭐ ⅶ 3 Summary
- LinkedList Is a double linked list to achieve List; - LinkedList It is also a double ended queue, which has the characteristics of queue, double ended queue and stack; - LinkedList Adding and deleting elements at the beginning and end of the queue is very efficient, and the time complexity is O(1); - LinkedList Adding and deleting elements in the middle is inefficient, and the time complexity is O(n); - LinkedList Random access is not supported, so it is inefficient to access non queue elements; - LinkedList Functionally equal to ArrayList + ArrayDeque;
- This is the way to learn the source code of Wenwen al
- 👍 If it helps you, give the blogger a free praise to encourage QAQ
- 👋 Blog home page 🎉 Winwin El learning house
- ⭐ More articles 👨🎓 Stay tuned to wenwendell's home page
- 🍅 Article release date: December 2021 sixteen
- 👋 java learning road!
- 🔎 For more articles, please pay attention to the personal home page!
- 🔎 List of popular articles:
- 🍅 [source code] super detailed ArrayList underlying source code + classic interview questions
- 🍅 HashMap underlying red black tree principle (super detailed diagram) + handwritten red black tree code
- 🍅 HashMap underlying source code analysis (super detailed illustration + interview questions)
- 🍅 HashMap underlying source code analysis (super detailed illustration)
