In a binary search tree implemented in a list of chains, each Node needs to be satisfied: left sub-Node < Node <=right sub-Node, preferably with a binary search height of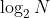The average time complexity for finding, adding, and deleting is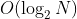In the worst case, the tree height constructed by inserting Node in some order is N, and the average time complexity for add-delete searches is O(N). The code is divided into Node classes, Binary Tree Abstract classes, and Binary Search Tree implementation classes. (

Catalog

BinaryNode class (Node for short)

BinaryTree Binary Tree abstract class (easy to expand later)

Intermediate traversal

BinarySearchTree (inherited from BinaryTree)

lookup

insert

Maximum/Minimum

delete

BinaryNode class (Node for short)

Node contains generic data that must implement Comparable join

Port, which is used to compare data within Node. Node itself implements the Comparable interface. When two Nodes compare, they directly call the compareTo method of their respective data. Node also needs to contain references to the parent Node and the left and right children Node, coded as follows:

package TreeStructure;

import org.jetbrains.annotations.NotNull;

public class BinaryNode<T extends Comparable> implements Comparable<BinaryNode<T>> {
    private T data;
    private BinaryNode<T> parent;
    private BinaryNode<T> leftChild;
    private BinaryNode<T> rightChild;

    public BinaryNode(T data) {
        this.data = data;
    }

    public BinaryNode(T data, BinaryNode<T> parent) {
        this.data = data;
        this.parent = parent;
    }

    @Override
    public int compareTo(@NotNull BinaryNode<T> tBinaryNode) {
        return this.data.compareTo(tBinaryNode.getData());
    }

    public void visit(){
        //Node access actions are written here
        System.out.print(data + " ");
    }

    public boolean hasChild(){
        if(this.getLeftChild() == null && this.getRightChild() == null) return false;
        else return true;
    }

    public boolean hasLeftChild(){
        if(this.getLeftChild() == null) return false;
        return true;
    }

    public boolean hasRightChild(){
        if(this.getRightChild() == null) return false;
        return true;
    }

    public boolean isLeftChildOf(BinaryNode<T> parentBinaryNode){
        if(parentBinaryNode != null && parentBinaryNode.getLeftChild() == this)return true;
        return false;
    }

    public boolean isRightChildOf(BinaryNode<T> parentBinaryNode){
        if(parentBinaryNode != null && parentBinaryNode.getRightChild() == this)return true;
        return false;
    }

    public BinaryNode<T> getParent() {
        return parent;
    }

    //Returns the minimum value in the right subtree of Node
    public BinaryNode<T> getSuccessor(){
        if(rightChild == null) return null;
        BinaryNode<T> current = rightChild;
        while(current.hasLeftChild())current = current.getLeftChild();
        return current;
    }

    public void setParent(BinaryNode<T> parent) {
        this.parent = parent;
    }


    public T getData() {
        return data;
    }

    public void setData(T data) {
        this.data = data;
    }

    public BinaryNode<T> getLeftChild() {
        return leftChild;
    }

    public void setLeftChild(BinaryNode<T> leftChild) {
        this.leftChild = leftChild;
    }

    public BinaryNode<T> getRightChild() {
        return rightChild;
    }

    public void setRightChild(BinaryNode<T> rightChild) {
        this.rightChild = rightChild;
    }
}

BinaryTree Binary Tree abstract class (easy to expand later)

Contains a reference (root) to the root Node by adding, deleting, and traversing in the order of before, after, and after. Since the method of traversing a binary tree in the order of before, after and after is the same, it can be implemented directly in this abstract class:

Intermediate traversal

For a binary tree with Node as its root, the left subtree is visited first, then the root is visited, and the right subtree is visited last. The treatment of the subtree is the same as that of the tree. When the root of the subtree Node is Null, the subtree is empty and can be used as the end condition for accessing it, thus traversing the whole tree recursively.

package TreeStructure;

public abstract class BinaryTree<T extends Comparable> {
    protected BinaryNode<T> root;

    public abstract BinaryNode<T> find(T key);

    public abstract void insert(T key);

    public abstract void delete(T key);

    //Ordered traversal starting with Node
    public void inOrder() {
        if (root != null) inOrder(root);
    }
    
    //Ordered traversal starting from a Node
    public void inOrder(BinaryNode<T> binaryNode) {

        if (binaryNode == null) return;
        BinaryNode<T> leftChild = binaryNode.getLeftChild();
        BinaryNode<T> rightChild = binaryNode.getRightChild();
        if (leftChild != null) inOrder(leftChild);
        binaryNode.visit();
        if (rightChild != null) inOrder(rightChild);
    }
    
    //Preorder
    public void preOrder() {
        if (root != null) inOrder(root);
    }

    public void preOrder(BinaryNode<T> binaryNode) {
        if (binaryNode == null) return;
        BinaryNode<T> leftChild = binaryNode.getLeftChild();
        BinaryNode<T> rightChild = binaryNode.getRightChild();
        binaryNode.visit();
        if (leftChild != null) preOrder(leftChild);
        if (rightChild != null) preOrder(rightChild);
    }
    
    //Postorder
    public void postOrder() {
        if (root != null) inOrder(root);
    }

    public void postOrder(BinaryNode<T> binaryNode) {
        if (binaryNode == null) return;
        BinaryNode<T> leftChild = binaryNode.getLeftChild();
        BinaryNode<T> rightChild = binaryNode.getRightChild();
        if (leftChild != null) postOrder(leftChild);
        if (rightChild != null) postOrder(rightChild);
        binaryNode.visit();
    }
}

BinarySearchTree (inherited from BinaryTree)

lookup

Suppose you look for a key, if root Node equals key, if root Node is larger than key, then look in the left subtree, if root Node is greater than or equal to key, then look in the right subtree, if subtree is null, then there is no key in the tree.

insert

Inserting a key less than the Node finds a location in the left subtree, and keys greater than or equal to the Node finds a location in the right subtree until the Node's subtree is null, where it is inserted.

Maximum/Minimum

Starting from root, find the last Node in the direction of the left subtree as the minimum, and the maximum is the same.

delete

Delete method is complex, there are three cases when Node is found to be deleted:

1. To delete a Node without a child Node, delete the Node directly.
2. To delete a Node that contains a child Node, delete the Node and connect its parent Node to the child Node
3. To delete a Node with two sub-Nodes, find the minimum value in the right subtree of the Node to be deleted as Successor. After the value of Successor overrides the Node to be deleted, delete the Successor. Successor cannot contain a left subtree. If it contains a left subtree, it means there is a smaller value than Successor, so use case 1 or 2 when deleting Successor.

package TreeStructure;

public class BinarySearchTree<T extends Comparable<T>> extends BinaryTree<T> {


    @Override
    public BinaryNode<T> find(T key) {
        if (root == null) return null;
        BinaryNode<T> current = root;
        while (current.getData().compareTo(key) != 0) {
            if (current.getData().compareTo(key) > 0) current = current.getLeftChild();
            else current = current.getRightChild();
            if (current == null) return null;
        }
        return current;
    }

    @Override
    public void insert(T key) {
        if (root == null)
            //No Node in the tree directly sets root to insert Node
            root = new BinaryNode<>(key);
        else {
            //Insert Node's parent Node
            BinaryNode<T> parent;
            //Traversing Node
            BinaryNode<T> current = root;
            do {
                parent = current;
                if (current.getData().compareTo(key) > 0) current = current.getLeftChild();
                    //Equal Node Inserts Right Subtree
                else current = current.getRightChild();
            } while (current != null);
            //Parent's child Node is null at this point, null is replaced by inserting Node
            if (parent.getData().compareTo(key) > 0) parent.setLeftChild(new BinaryNode<>(key, parent));
            else parent.setRightChild(new BinaryNode<>(key, parent));
        }
    }

    @Override
    public void delete(T key) {
        //Node to be deleted
        BinaryNode<T> delete = find(key);
        if (delete == null) return;

        if (delete.hasChild()) {
            if (delete.hasLeftChild() && delete.hasRightChild()) {
                //delete has two children
                BinaryNode<T> successor = delete.getSuccessor();
                delete.setData(successor.getData());
                if (successor.hasRightChild()) {
                    //successor has right child nodes
                    successor.getRightChild().setParent(successor.getParent());
                    if (delete == root) return;
                    if (successor.isRightChildOf(successor.getParent()))
                        successor.getParent().setRightChild(successor.getRightChild());
                    else
                        successor.getParent().setLeftChild(successor.getRightChild());
                } else {
                    if (successor.isRightChildOf(successor.getParent()))
                        successor.getParent().setRightChild(null);
                    else
                        successor.getParent().setLeftChild(null);
                }
            } else {
                //delete has a Child
                if(delete == root){
                    //delete is root
                    if(root.hasLeftChild()) root = root.getLeftChild();
                    else root = root.getRightChild();
                    root.setParent(null);
                }
                else{
                    //Parent Node of delete
                    BinaryNode<T> parent = delete.getParent();
                    if (delete.isLeftChildOf(parent)) {
                        if (delete.hasLeftChild()) {
                            parent.setLeftChild(delete.getLeftChild());
                            delete.getLeftChild().setParent(parent);
                        } else {
                            parent.setLeftChild(delete.getRightChild());
                            delete.getRightChild().setParent(parent);
                        }
                    } else {
                        if (delete.hasLeftChild()) {
                            parent.setRightChild(delete.getLeftChild());
                            delete.getLeftChild().setParent(parent);
                        } else {
                            parent.setRightChild(delete.getRightChild());
                            delete.getRightChild().setParent(parent);
                        }
                    }
                }
            }
        } else {
            //delete has no child Node
            if (delete == root) root = null;
            else{
                //Parent Node of delete
                BinaryNode<T> parent = delete.getParent();
                if (delete.isLeftChildOf(parent)) parent.setLeftChild(null);
                else parent.setRightChild(null);
            }

        }

    }

    public BinaryNode<T> minimum() {
        if (root == null) return null;
        BinaryNode<T> current = root;
        while (current.getLeftChild() != null) current = current.getLeftChild();
        return current;
    }

    public BinaryNode<T> maximum() {
        if (root == null) return null;
        BinaryNode<T> current = root;
        while (current.getRightChild() != null) current = current.getRightChild();
        return current;
    }
}