OJ question

First, let's understand the forms of OJ questions. There are two forms:
- Interface type
Provide an interface function instead of a complete program. Just implement this function. After submitting the program, this code will be submitted to the OJ server, and it will be merged with other test programs (header file and main function)
Test cases generally interact through parameters and return values.
- IO type
Write the code area without giving you anything. Write your own complete program, header file, main function, algorithm logic
We need to input test cases for interface IO and output the structure in format
OJ exercise of complexity
1. Disappearing figures
Title Description:
The array nums contains all integers from 0 to N, but one of them is missing. Please write code to find the missing integer. Do you have a way to finish it in O(n) time?
Example 1:
Input: [3,0,1]
Output: 2
Example 2:
Input: [9,6,4,2,3,5,7,0,1]
Output: 8
Title Source: Disappearing numbers
Solution 1:
Sort first, and then find out whether the previous number + 1 is equal to the next number. If it is equal to, continue. If it is not equal to this number, it is the missing number
However, the complexity does not meet the requirements. qsort fast scheduling, time complexity O(N*logN), and the title requirement is O(n), so let's look at the next solution:
Solution 2:
Sum, loop to calculate 0 + 1 + 2 +... + n, subtract the values in the array, and the accumulation is the missing number
The code is as follows:
int missingNumber(int* nums,int numssize)
{
int i=0;
int sum=0;
int sum1=0;
for(i=0;i<numssize;i++)
{
sum+=nums[i];
}
for(i=1;i<=numssize;i++)
{
sum1+=i;
}
return sum1-sum;
}
First calculate the sum of all the numbers in the array, and then calculate the sum of 0-numsize. Subtraction is the missing number.
Solution 3:
Before we look at the idea of solution 3, we need to know that two identical number XORs are equal to 0, 0 and any number XOR is equal to itself
For example, 3 exclusive or 3, the difference is 1, and their binary bits are the same, so they are all 0, so they are equal to 0
Solution 3 idea:
Create a variable x=0. X first follows the XOR of the value in the array, and then follows the XOR of the number between 0-n. it is equivalent to that other numbers appear twice. The XOR of both times becomes 0, and the missing number only appears once. Therefore, it is best that x is the missing number
Time complexity O(N), meeting the requirements
The code is as follows:
int missingnumber(int* nums,int numssize)
{
int x=0;
//XOR with the value of the array first
for(int i=0;i<numssize;i++)
{
x^=nums[i];
}
//Then XOR with the number 0-n
for(int i=0;i<=numssize;i++)
{
x^=i;
}
return x;
}
2. Rotate array
Title Description:
Given an array, move the elements in the array K positions to the right, where k is a non negative number.
Advanced:
Think of as many solutions as possible. There are at least three different ways to solve this problem.
Can you use the in-situ algorithm with spatial complexity O(1) to solve this problem?
Example 1:
Input: nums = [1,2,3,4,5,6,7], k = 3
Output: [5,6,7,1,2,3,4]
Explanation:
Rotate one step to the right: [7,1,2,3,4,5,6]
Rotate 2 steps to the right: [6,7,1,2,3,4,5]
Rotate 3 steps to the right: [5,6,7,1,2,3,4]
Title Source: Rotate array
Solution 1:
Rotate right once: keep the last value to the temp variable, move the value of the array to the right once, and then put temp to the far left
Then set a layer of circulation on the outside, right-handed k times
Time complexity: 0 (n (k% n)) - > when K==N, the time complexity is O(1), and the worst is O(N^2). When K==N-1, the time complexity considers the worst case, so the time complexity is O(N^2). The time performance of this method is not high*
Space complexity is O(1)
The code is as follows:
void rotate(char*str,int k)
{
int i=0;
int len=strlen(str)
for(i=0;i<k%len;i++)
{
char temp=str[len-1]
int j=0;
for(j=len-1;j>0;j--)
{
str[j]=str[j-1];
}
str[0]=temp;
}
}
What needs to be considered here is that when k is equal to len, it is equivalent to no rotation, so the termination condition of the external for loop here is I < K% len.
Solution 2:
Idea:
This is the solution of space for time, using two arrays: directly put the last K on the first k of the second array, and the first n-k on the back of the second array
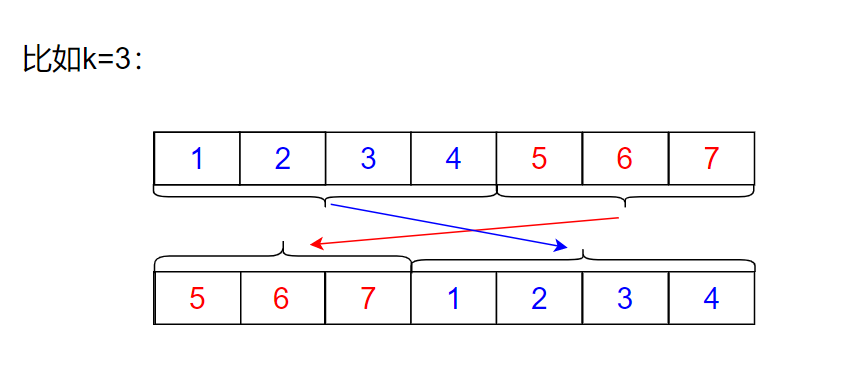
The code is as follows:
int main()
{
int arr1[] = { 1,2,3,4,5,6,7 };
int arr2[10] = { 0 };
int k = 0;
scanf("%d", &k);
int sz = sizeof(arr1) / sizeof(arr1[0]);
int i = 0;
//Put the last K numbers on the first k of the second array
for (i = 0; i < k; i++)
{
arr2[i] = arr1[sz - k + i];
}
//Put the first n-k numbers after the second array
for (i = 0; i < sz - k; i++)
{
arr2[k + i] = arr1[i];
}
for (i = 0; i < sz; i++)
{
printf("%d ", arr2[i]);
}
return 0;
}
Time complexity: O(N)
Space complexity: O(N)
This can solve this problem, but this OJ question cannot be written like this, because this OJ question is interface type:
We put the elements of array 1 in array 2. We didn't change the rotation of array 1, but put the rotation result of array 1 in array 2. Moreover, the return value of this function is void, and we can't return array 2. It's good if we have this idea. This is a solution, but it can't be passed.
Let's look at solution 3. This is the optimal solution
Solution 3: three step turnover method
1. Invert the first n-k numbers
2. Inverse of the last k numbers
3. Global inversion
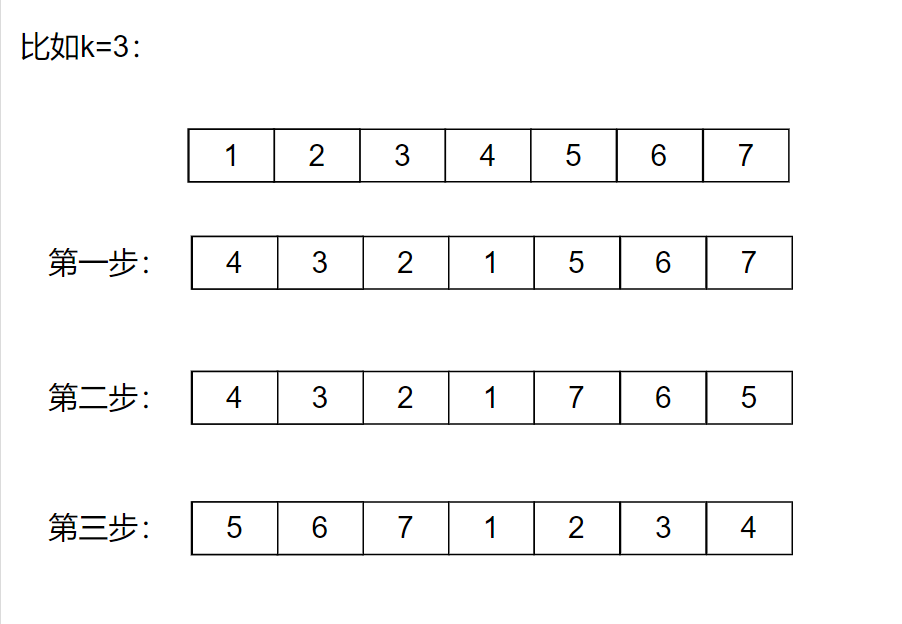
void reverse(int *nums,int begin,int end)
{
while(begin<end)
{
int temp=nums[begin];
nums[begin]=nums[end];
nums[end]=temp;
begin++;
end--;
}
}
void rotate(int *nums,int numssize,int k)
{
k%=numssize;
reverse(nums,0,numssize-k-1);
//Invert the first n-k numbers
reverse(nums,numssize-k,numssize-1);
//Inverse of the last k numbers
reverse(nums,0,numssize-1);
//Global inversion
}
The time complexity of this solution: O(N) and space complexity: O(1) are optimal. It is recommended that you write the third solution, and the code is not difficult. You only need to write an inverse function. You only need to pay attention to the clear grasp of the first n-k and last K parameters when transmitting inverse parameters.
Let's look at some OJ questions in the sequence table array:
Array related OJ questions
1. Remove element
Title Description:
Give you an array num and a value val. you need to remove all elements with a value equal to Val in place and return the new length of the removed array.
Instead of using extra array space, you must use only O(1) extra space and modify the input array in place.
The order of elements can be changed. You don't need to consider the elements in the array that exceed the new length.
Title Source: Removing Elements
Remove all elements val in the array in place. The time complexity is O(N) and the space complexity is O(1)
Idea 1:
Traverse the array, encounter the val value, move the following data to a unit and delete it
Time complexity: O(N^2)
Space complexity: O(1)
int removeElement(int* nums, int numsSize, int val)
{
int i = 0;
int temp = numsSize;
//1234546
for (i = 0; i < numsSize; i++)
{
if (nums[i] == val)
{
int begin = i;
while (begin<numsSize-1)
{
nums[begin] = nums[begin + 1];
begin++;
}
temp--;//Number of current elements of the array
i--;
numsSize--;
}
}
return temp;
}
//Test code
int main()
{
int nums[]={1,2,3,4,5,4,6};
int numsSize=sizeof(nums)/sizeof(nums[0]);
int ret = removeElement(nums,numsSize,4);
for(int i=0;i<ret;i++)
{
printf("%d ",nums[i]);
}
return 0;
}
After moving the data every time, we need to move i –. At this time, the i value of the subscript is the subscript of val, and the elements behind val move forward. At this time, the i subscript corresponds to the next element of val, so we should keep i unchanged and continue to traverse. At the same time, the number of traversals should be less to prevent crossing the boundary. We should also let numsize –, temp record the number of elements.
Idea 2:
Space for time: copy all values that are not 3 in the original array to the new array, and then copy them back. The time complexity O(N) and space complexity O(N) only do not meet the requirements of the question, because the space complexity of the question requires O(N)
We can only know this idea here. This idea cannot solve this problem, because the complexity of the topic space requires O(N). The test code of idea 2 is as follows:
int removeElement(int* nums1, int* nums2, int numsSize, int val)
{
int i = 0;
int temp = 0;
for (i = 0; i < numsSize; i++)
{
if (nums1[i] != val)
{
nums2[i] = nums1[i];
temp++;
}
else
{
nums2--;
}
}
return temp;
}
int main()
{
int nums1[] = { 1,2,3,4,5,4,6 };
int nums2[8] = {0};//1,2,3,5,6
int numsSize = sizeof(nums1) / sizeof(nums1[0]);
int ret = removeElement(nums1, nums2, numsSize, 4);
for (int i = 0; i < ret; i++)
{
printf("%d ", nums2[i]);
}
return 0;
}
The best idea is given below:
Idea 3:
Give two pointers dest and src to point to the starting position. src finds the position that is not val and puts it at the position pointed by dest. Time complexity: O(N), space complexity: O(1)
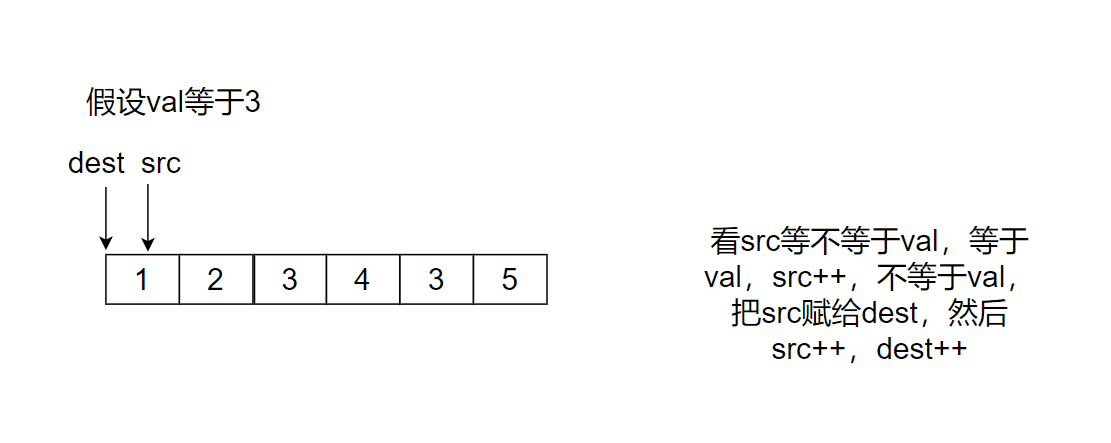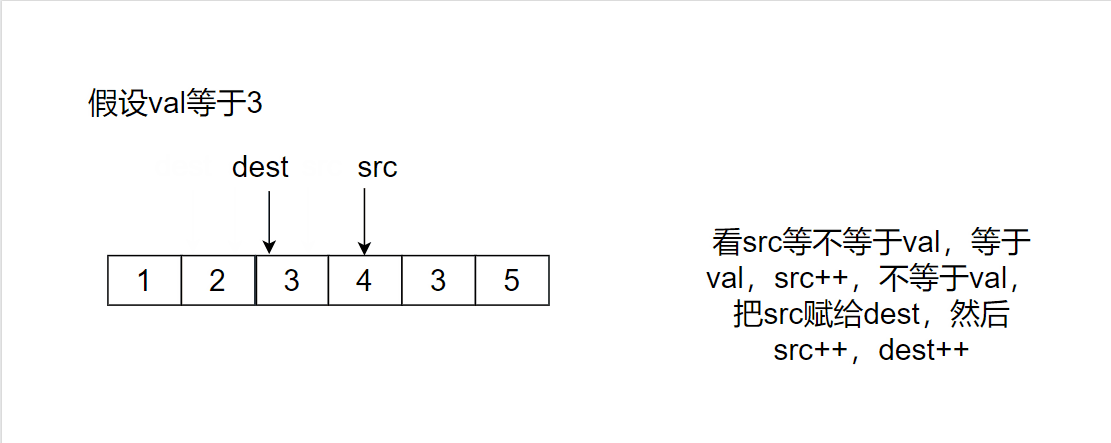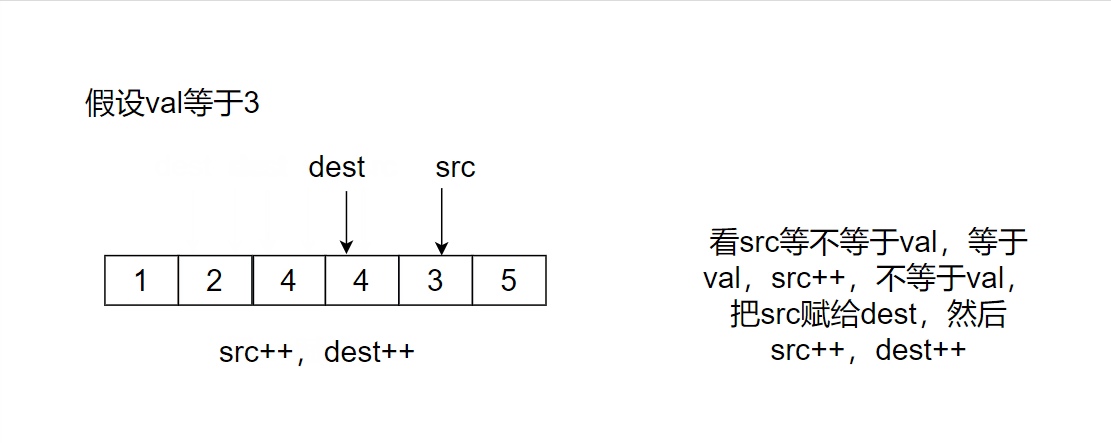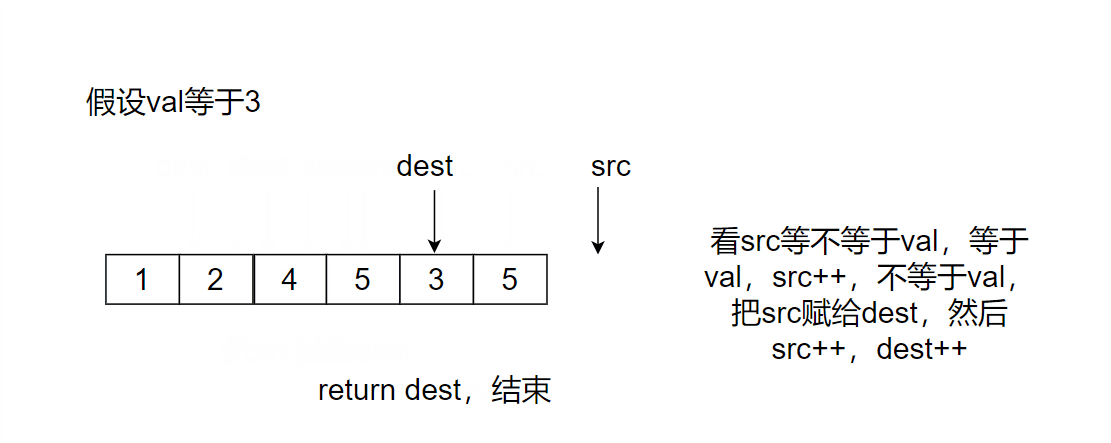
src stops when pointing out of the array, and then returns dest, which happens to be the array after deleting the val value
The code is as follows:
int removeElement(int *nums,int numsSize)
{
int src=0,dest=0;
while(src<numssize)
{
if(nums[src]==val)
{
src++;
}
else
{
nums[dest]=nums[src];
src++;
dest++;
}
}
return dest;
}
2. Delete duplicate values in the ordered array
Title Description:
Give you an ordered array nums, please delete the repeated elements in place, make each element appear only once, and return the new length of the deleted array.
Do not use additional array space. You must modify the input array in place and complete it with O(1) additional space.
Example 1:
Input: num = [1,1,2]
Output: 2, Num = [1,2]
Explanation: the function should return a new length of 2, and the first two elements of the original array num are modified to 1 and 2. There is no need to consider the elements in the array that exceed the new length.
Example 2:
Input: num = [0,0,1,1,1,2,2,3,3,4]
Output: 5, Num = [0,1,2,3,4]
Explanation: the function should return a new length of 5, and the first five elements of the original array num are modified to 0, 1, 2, 3 and 4. There is no need to consider the elements in the array that exceed the new length.
Title Source: Removes duplicate values from an ordered array
Idea:
src finds a value that is not equal to dest. src + + is not found. Dest + + is found. Put src into dest and then src++
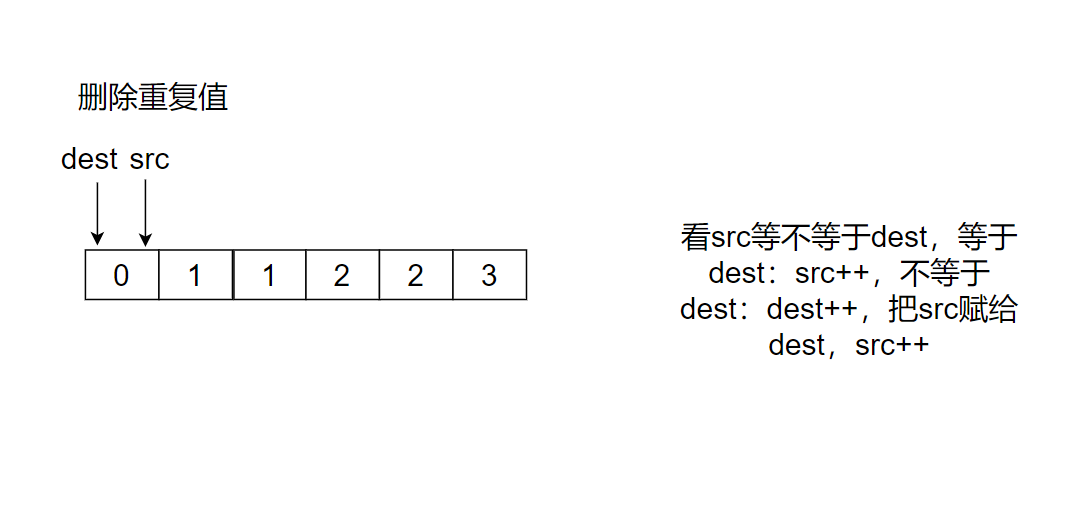
The code is as follows:
int removeDuplicates(int* nums, int numsSize){
int src=0;
int dest=0;
if(numsSize==0)
{
return 0;
}
while(src<numsSize)
{
if(nums[src]==nums[dest])
{
src++;
}
else
{
dest++;
nums[dest]=nums[src];
src++;
}
}
return dest+1;//Returns the length of the array
}
3. Merge two ordered arrays
Title Description:
Here are two ordered integer arrays nums1 and nums2. Please merge nums2 into nums1 to make nums1 an ordered array. The number of elements initializing nums1 and nums2 is m and n, respectively. You can assume that the space size of nums1 is equal to m + n, so it has enough space to store elements from nums2.
Example 1:
Input: nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3
Output: [1,2,2,3,5,6]
Example 2:
Input: nums1 = [1], m = 1, nums2 = [], n = 0
Output: [1]
Title Source: Merge two arrays
Idea:
Solution 1: copy nums2 data to nums1, qsort quickly arrange nums1, and the time complexity is (m+n)*log(m+n)
Solution 2: open up a new m+n array, merge two small arrays, compare the values of the two arrays from scratch, put the small array into the new array, and then copy it to nums1, time complexity O (m+n), space complexity O (m+n)
Solution 3: take the larger one in turn and put it into nums1 from back to front
Here we explain solution 3:
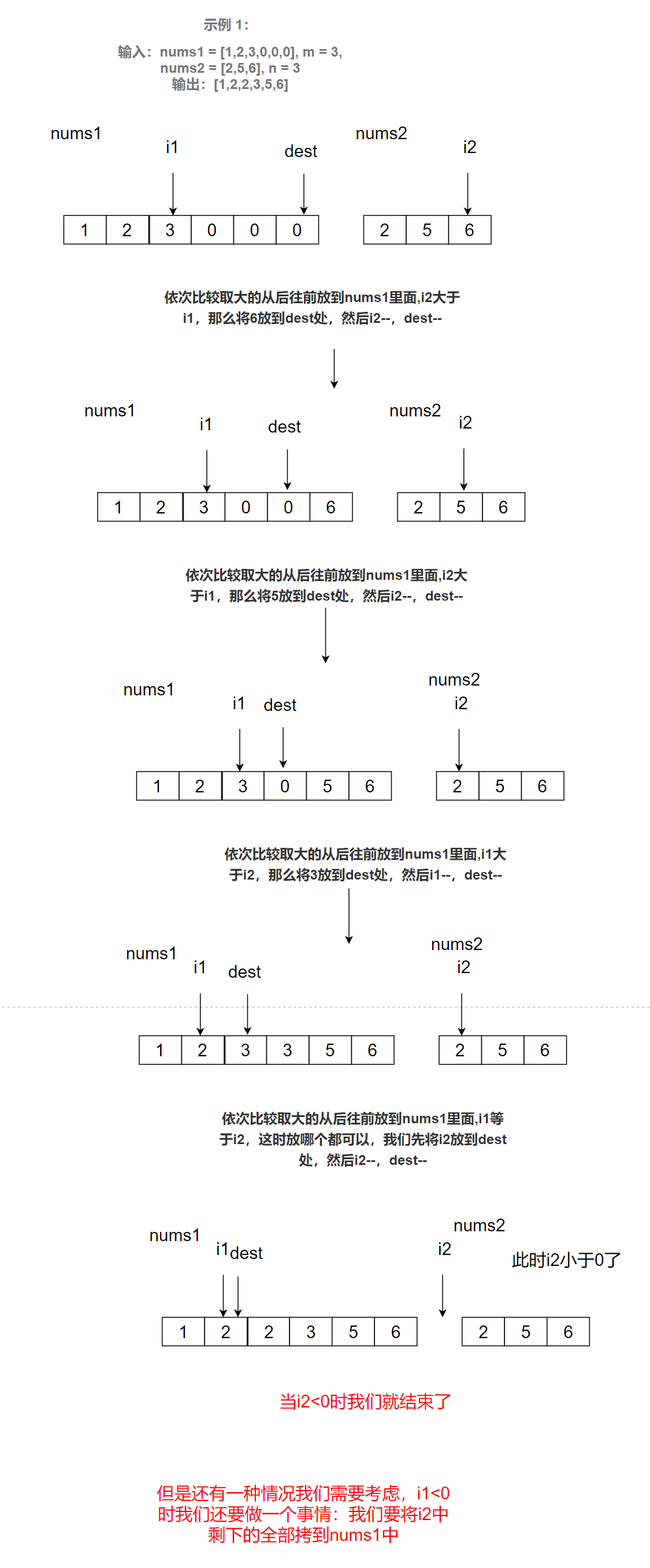
After the above analysis, the code is as follows:
void merge(int* nums1, int nums1Size, int m, int* nums2, int nums2Size, int n){
int i1 = m-1,i2 = n-1;
int dest=m+n-1;
while(i1>=0 && i2>=0)//Continue when both are greater than or equal to 0
{
if(nums1[i1]>nums2[i2])//Take the big one and put it behind nums1
{
nums1[dest--]=nums1[i1--];
}
else
{
nums1[dest--]=nums2[i2--];
}
}
//If I2 < 0 and nums2 copy ends, the processing ends, because the remaining number is already in nums1
//If nums1 ends, move the data of nums2
while(i2>=0)
{
nums1[dest--]=nums2[i2--];
}
}
It should be noted that:
If I2 < 0 and nums2 copy ends, the processing ends, because the remaining number is already in nums1
If nums1 ends, move the data of nums2
How do we analyze OJ procedures when OJ reports errors?
-
If not, first get used to reading the code with the test cases it reports errors to
-
Copy the code to vs, supplement other codes, and test with unprecedented tests
Linked list OJ question
1. Remove linked list elements
Title Description:
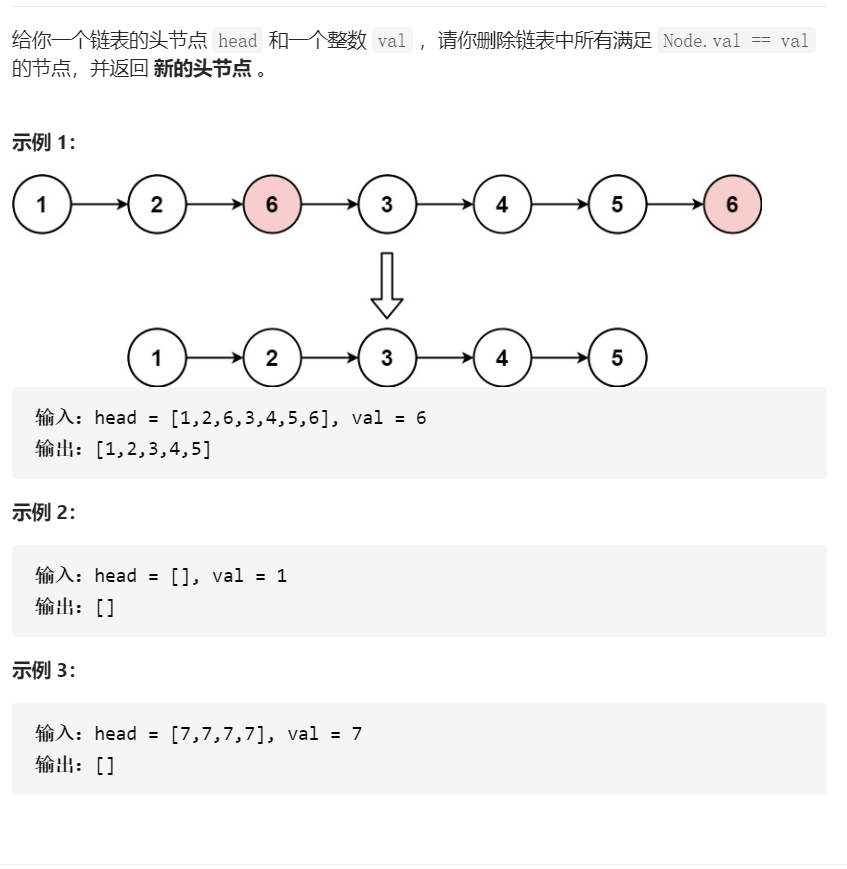
Title Source: Remove linked list elements
Idea 1: insert the end of all values in the linked list that are not Val into the new linked list and delete nodes equal to val
Train of thought analysis:
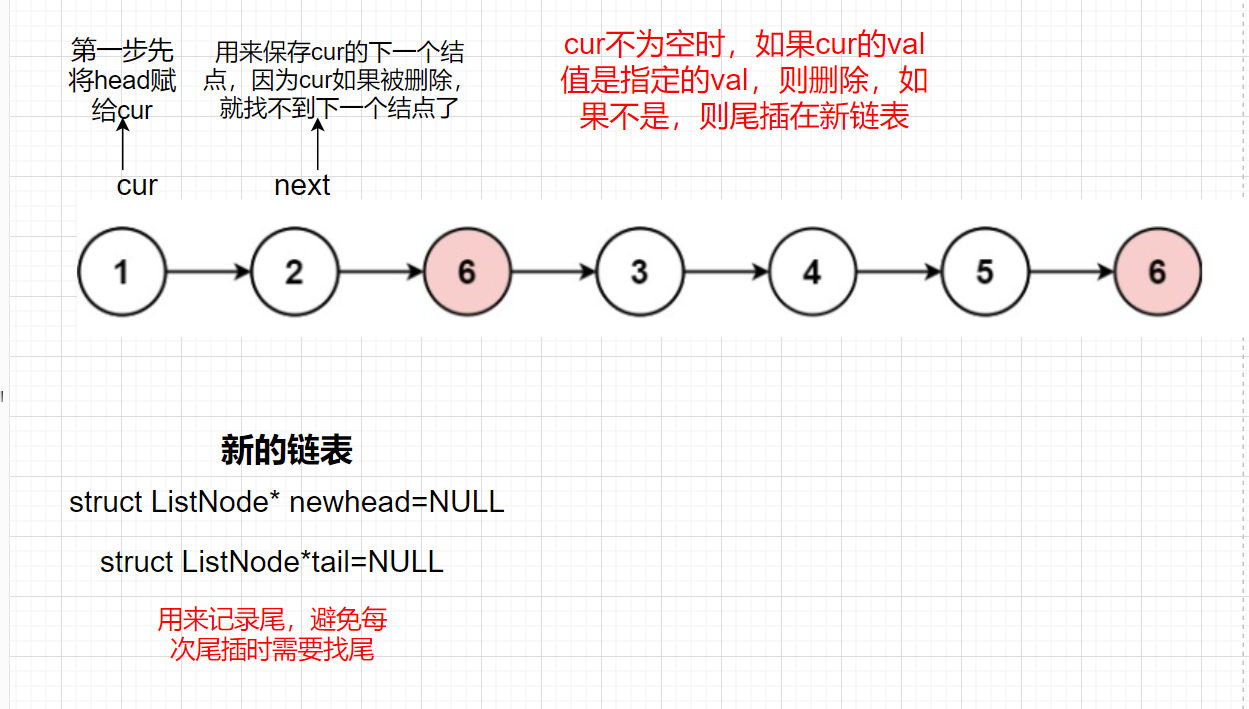
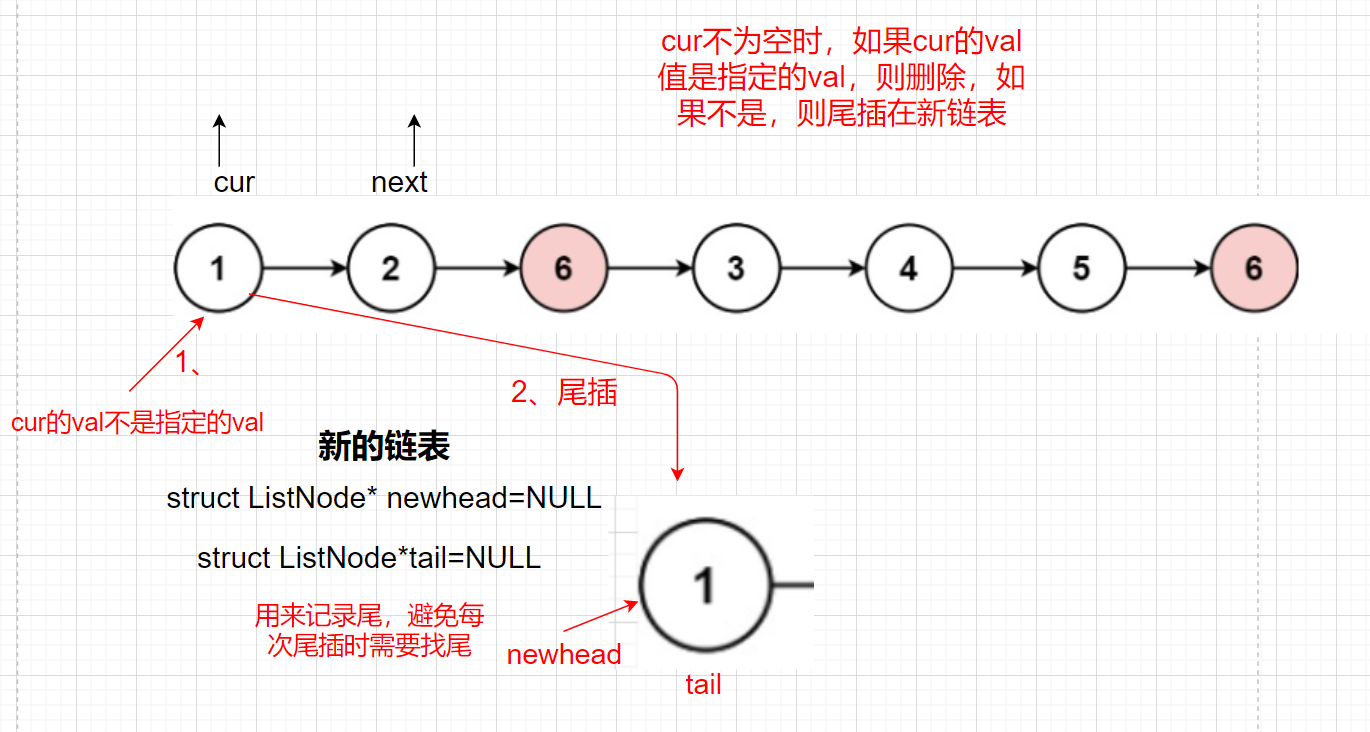
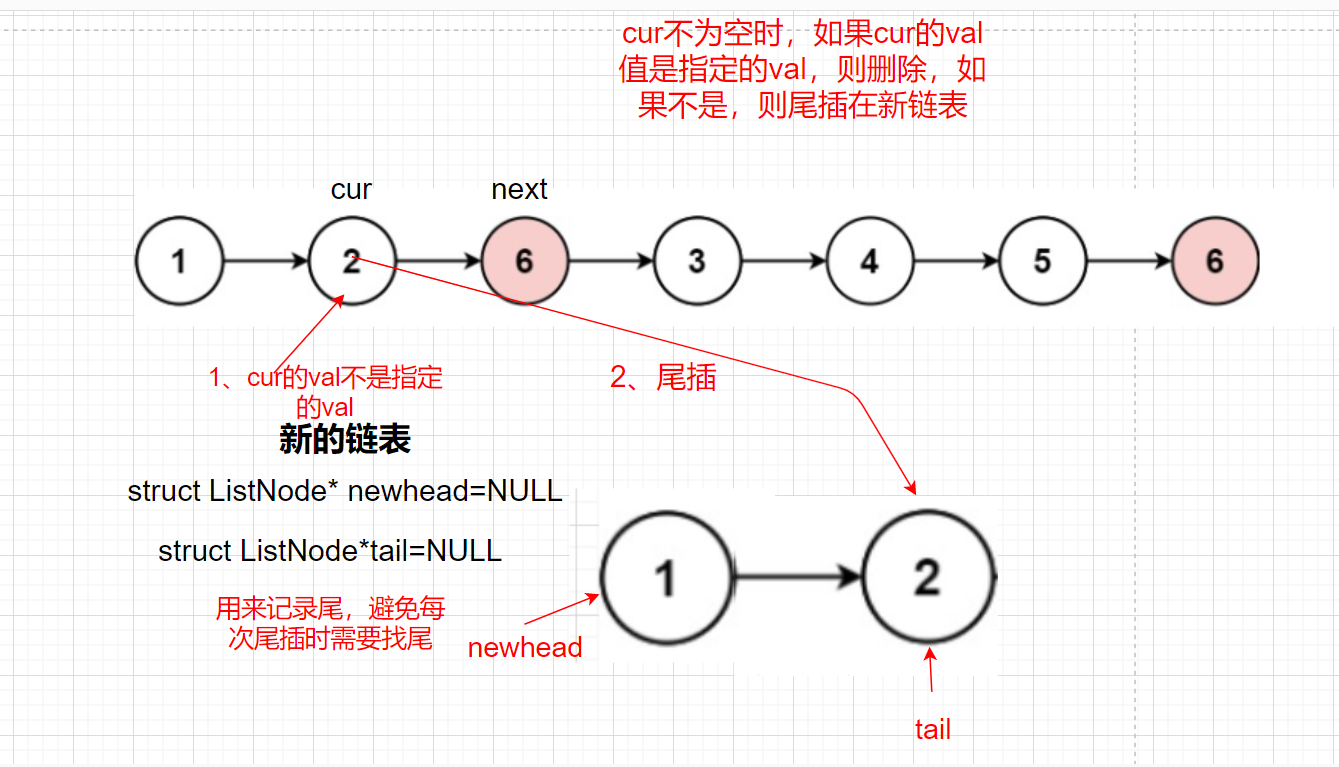
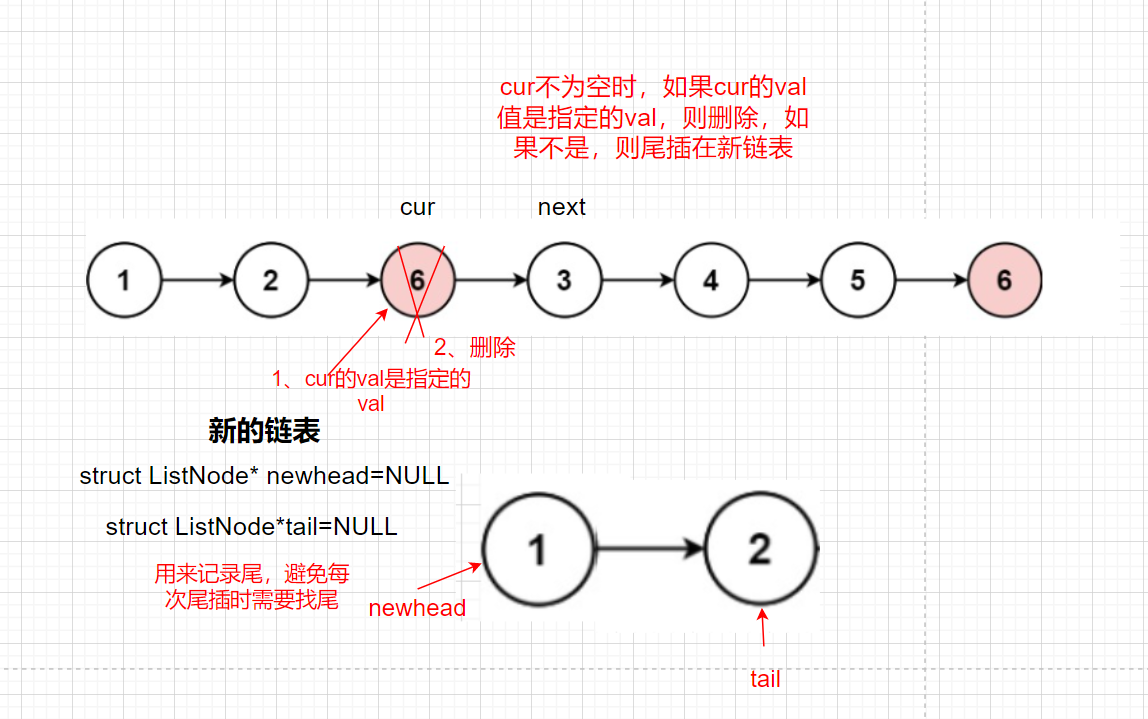
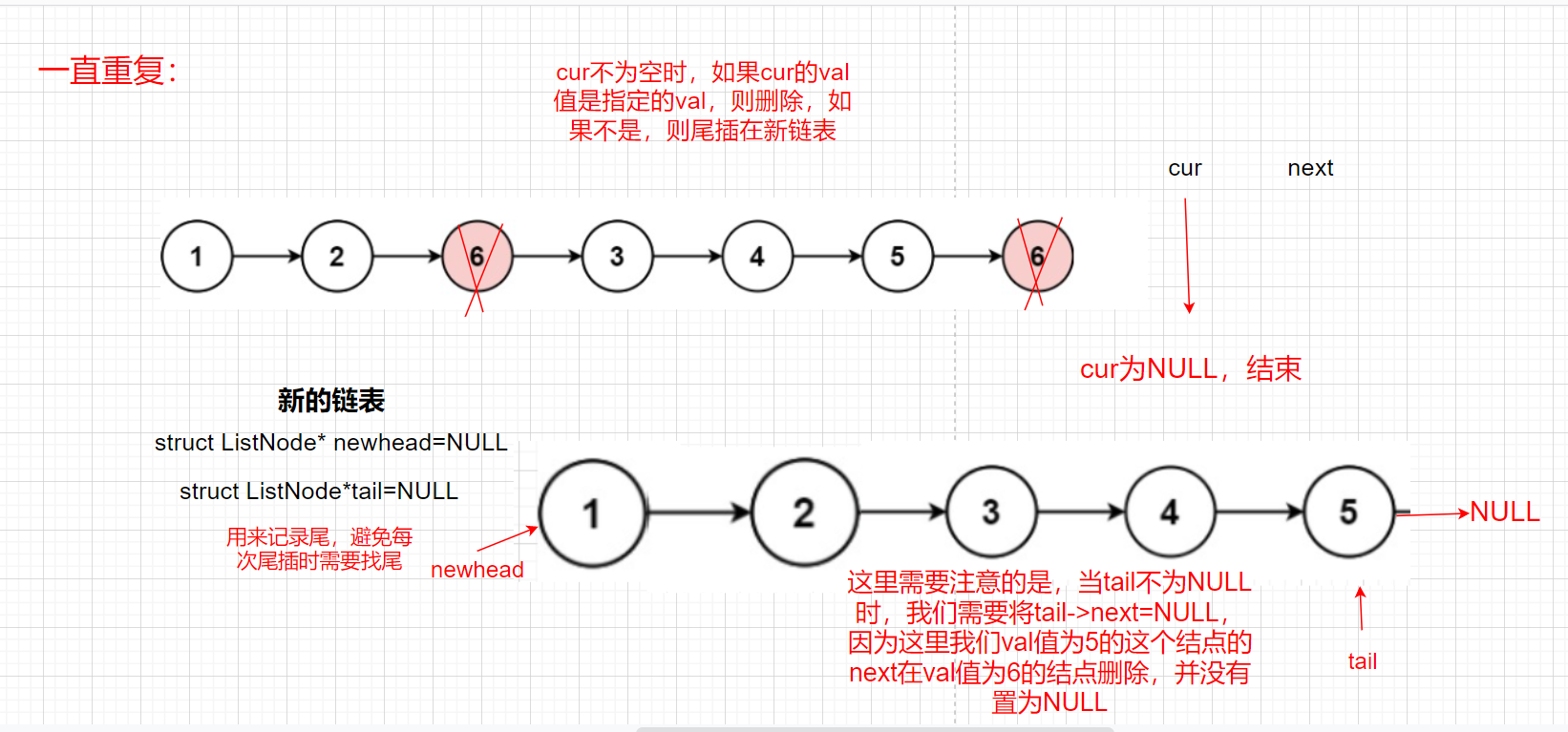
In addition, we need to consider the case that the head passed in is NULL. If the head is NULL, we directly return NULL
The code of idea 1 is as follows:
struct ListNode* removeElements(struct ListNode* head, int val)
{
if(head==NULL)
{
return NULL;
}
struct ListNode*newhead=NULL,*tail=NULL;//The head node and record tail node of the new linked list
//val deletes it, not inserts the tail of val into the new linked list
struct ListNode*cur=head;
while(cur)
{
struct ListNode* next=cur->next;//It is convenient to find the next node of the current node and define a next
if(cur->val==val)//Yes val delete
{
free(cur);
}
else//Not for tail insertion
{
//When tail is NULL, there is no element
if(tail==NULL)//Trailing first element
{
newhead=cur;
tail=cur;
}
else
{
tail->next=cur;
tail=cur;
}
}
cur=next;
}
//When the data of the last node in the linked list is val and the previous node is not val, we insert the tail of the previous node into the new linked list and delete the last node. However, we do not set the next of the previous node to NULL, so we need to empty it here; And we need to judge whether the tail is NULL or not before we can perform this operation. When the val values of the linked list are all the val values specified for deletion, there is no tail inserted into the new linked list element. At this time, the tail is NULL, so we can't set the next of the tail to NULL
if(tail)
{
tail->next=NULL;
}
return newhead;
}
It should be noted that:
When the data of the last node in the linked list is val and the previous node is not val, we insert the tail of the previous node into the new linked list and delete the last node. However, we do not set the next of the previous node to NULL, so we need to empty it here; And we need to judge whether the tail is NULL or not before we can perform this operation. When the val values of the linked list are all the val values specified for deletion, there is no tail inserted into the new linked list element. At this time, the tail is NULL, so we can't set the next of the tail to NULL
Idea 2: cur finds the node where val is located, prev records the previous node, and deletes the linked list. To delete the linked list, you need to find the previous node of the deleted node

struct ListNode* removeElements(struct ListNode* head, int val)
{
if (head == NULL)
{
return NULL;
}
struct ListNode* cur = head;
struct ListNode* prev = head;
while (cur)
{
while ( cur && (cur->val) != val )
{
prev = cur;//Record the previous node of the current node
cur = cur->next;
}
//There are two situations when "while" comes out: 1. Cur is NULL, which means that it is over. 2. (cur - > VAL) = = Val, which should be deleted at this time
if(cur==NULL)
{
return head;
}
//Find val, delete
if (cur == head)//If the first value is val, delete the header
{
struct ListNode* newhead = cur->next;
free(cur);
cur = newhead;
head = newhead;
}
else//Subsequent deletion
{
prev->next = cur->next;
free(cur);
cur = prev->next;
}
}
return head;
}
Define a cur and prev to traverse. Prev records the previous node of cur. Cur is not empty. Enter the loop, and then use a loop to find the node with val value. When it comes out, there are two situations: 1. Cur is NULL, indicating that it is over. 2. (cur - > val) = = val, which should be deleted at this time; Therefore, it is necessary to judge whether cur is NULL. If cur is NULL, it will directly return to head. Otherwise, the node will be deleted, and the deletion will be divided into header deletion and non header deletion.
2. Reverse linked list
Title Description:
Give you the head node of the single linked list. Please reverse the linked list and return the reversed linked list.
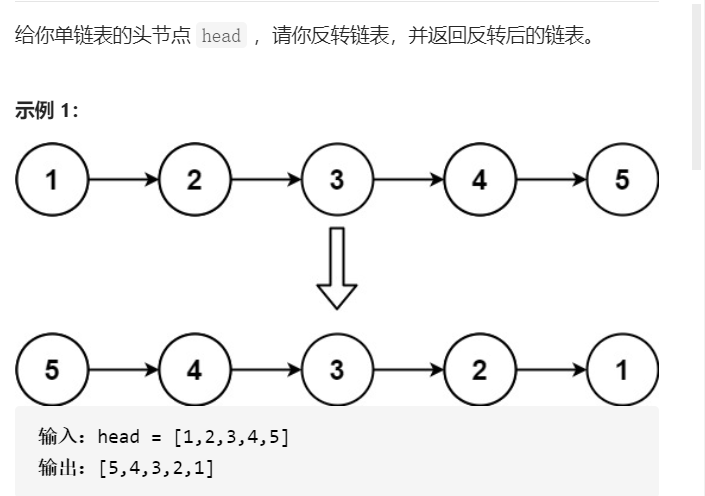
Title Source: Reverse linked list
**Idea 1: * * adjust the direction of node pointer, reverse the direction of n1 and n2, and iterate with n3
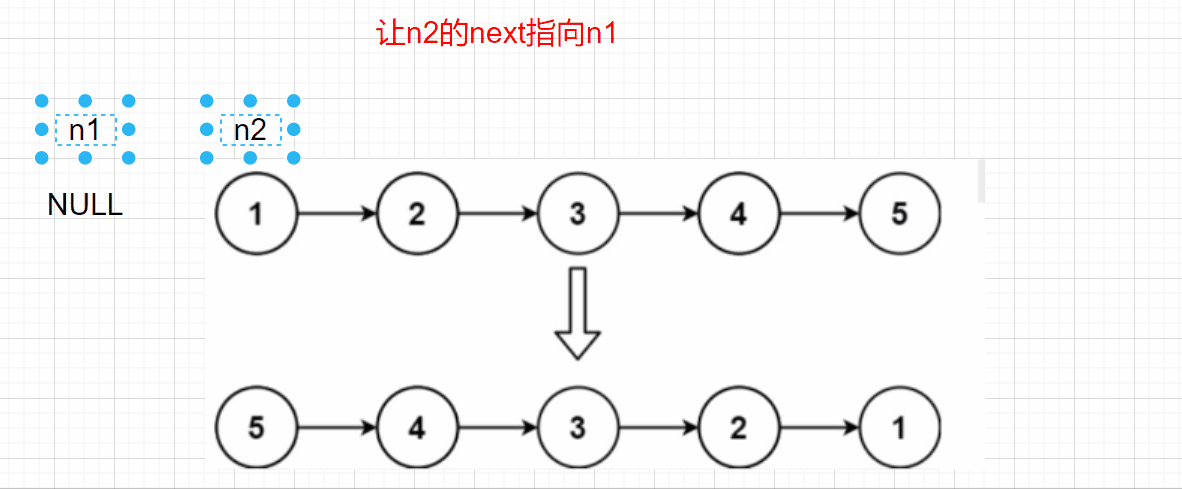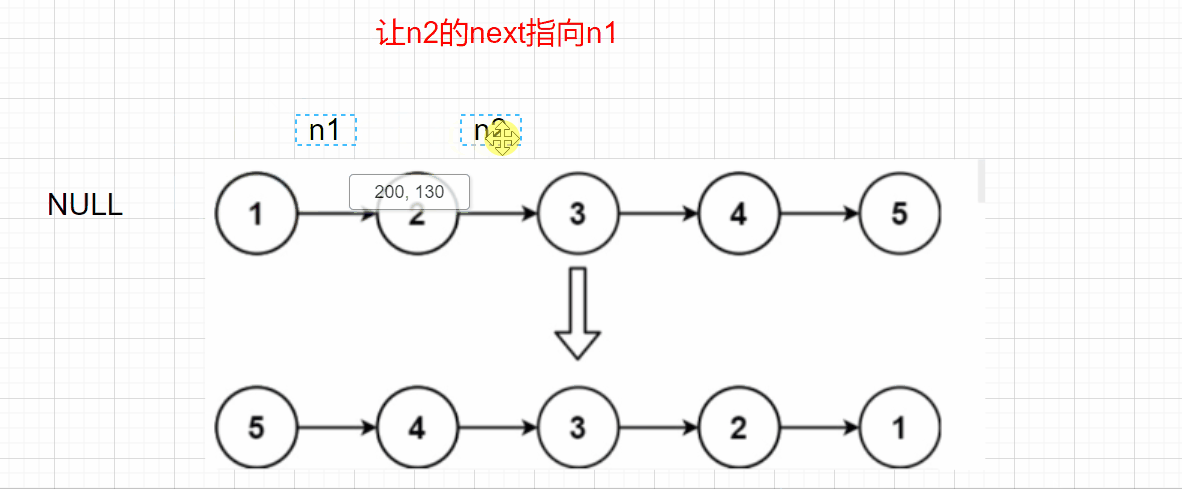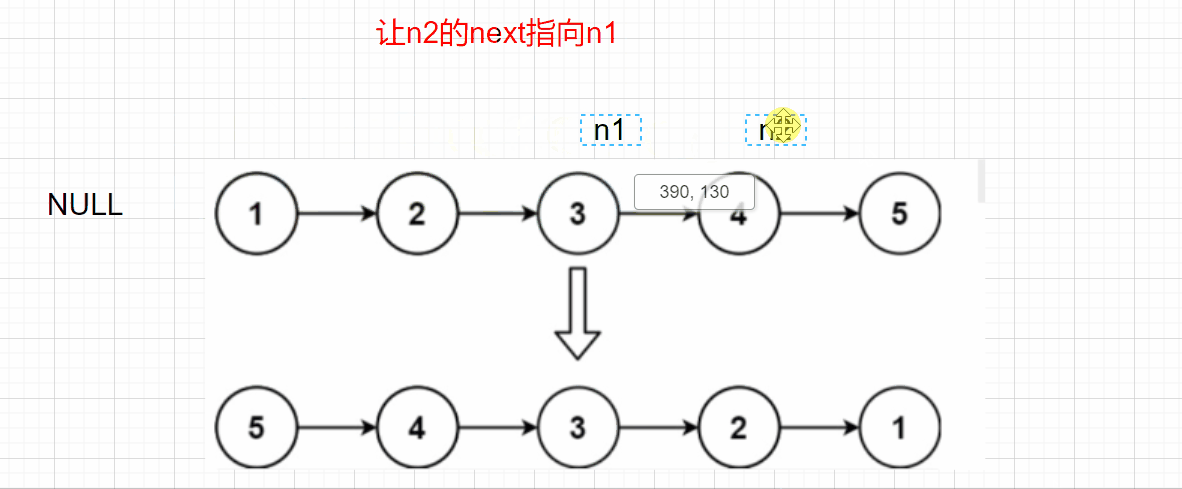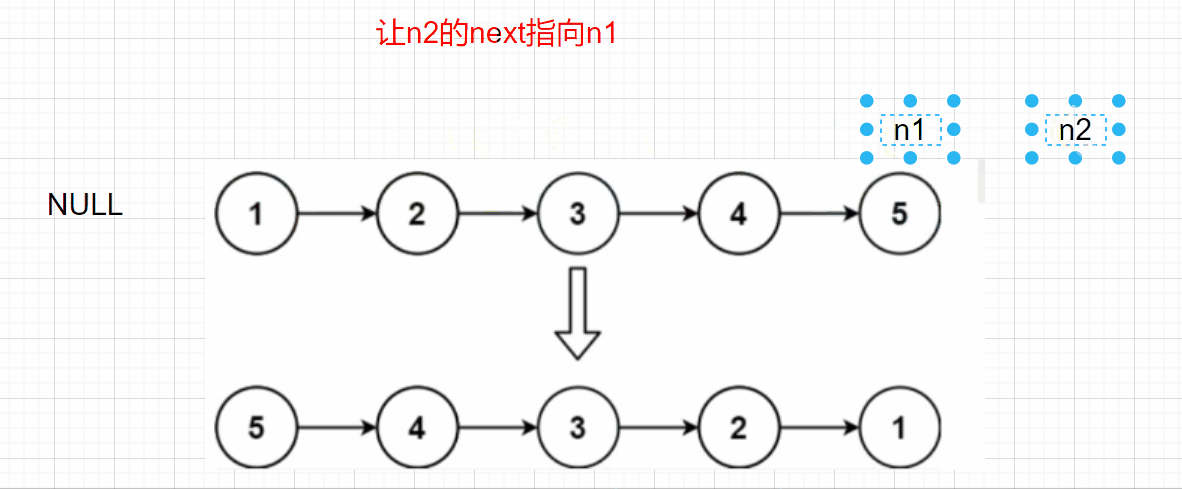
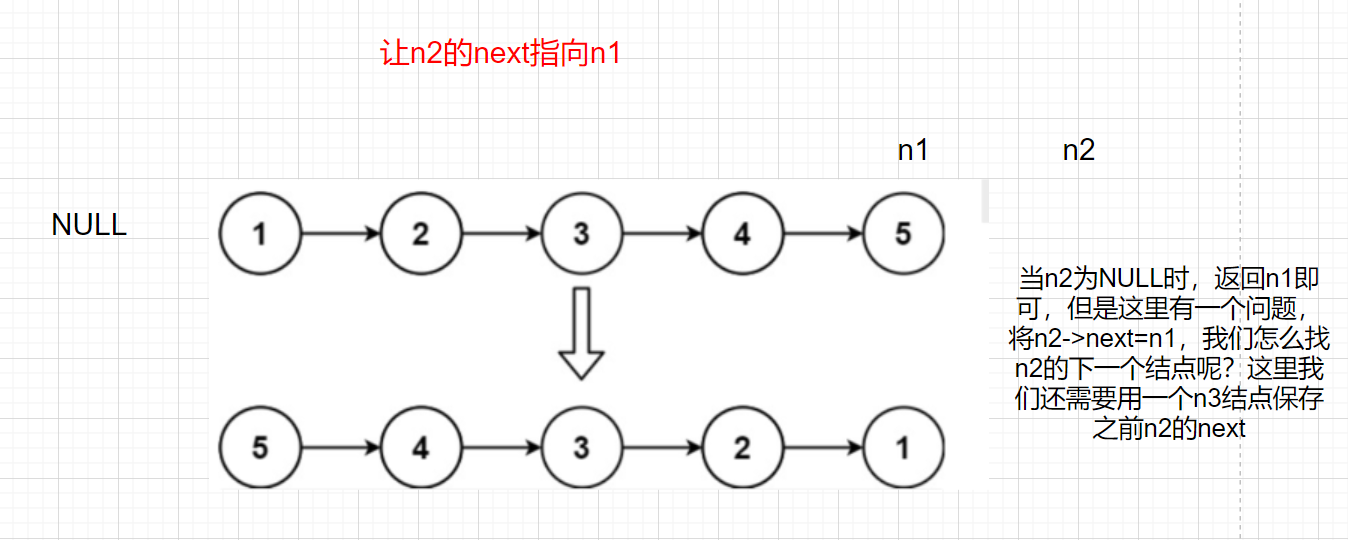
When n2 is NULL, n1 can be returned, but there is a problem. If n2 - > next = n1, how can we find the next node of n2? Here, we also need to use an n3 node to save the previous n2 next
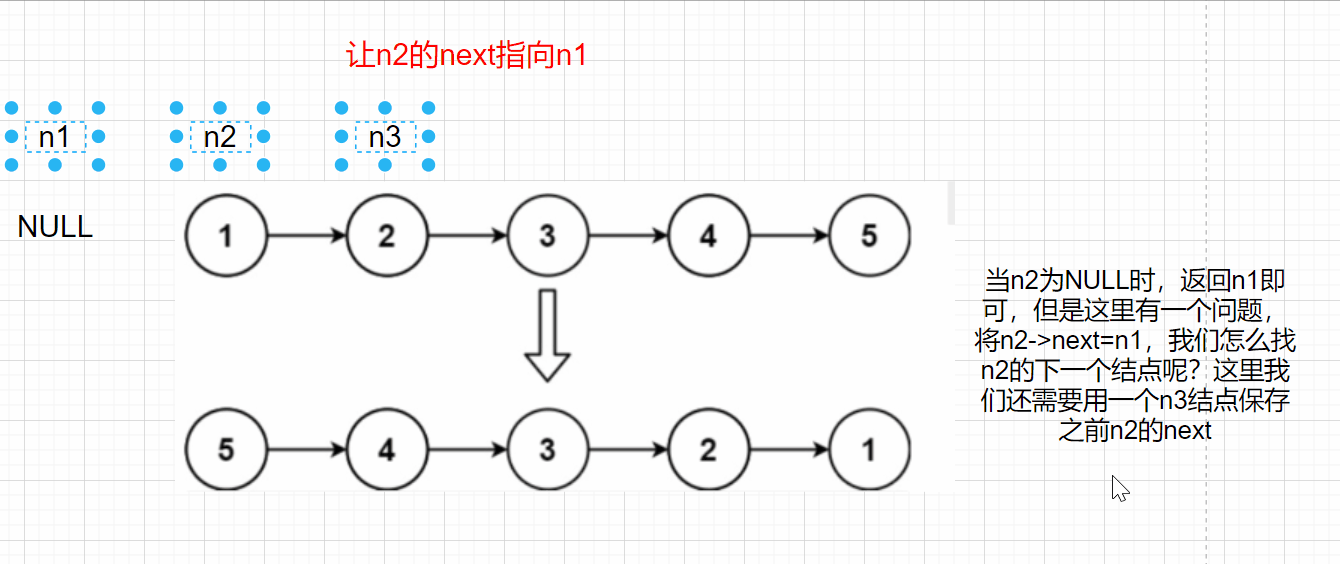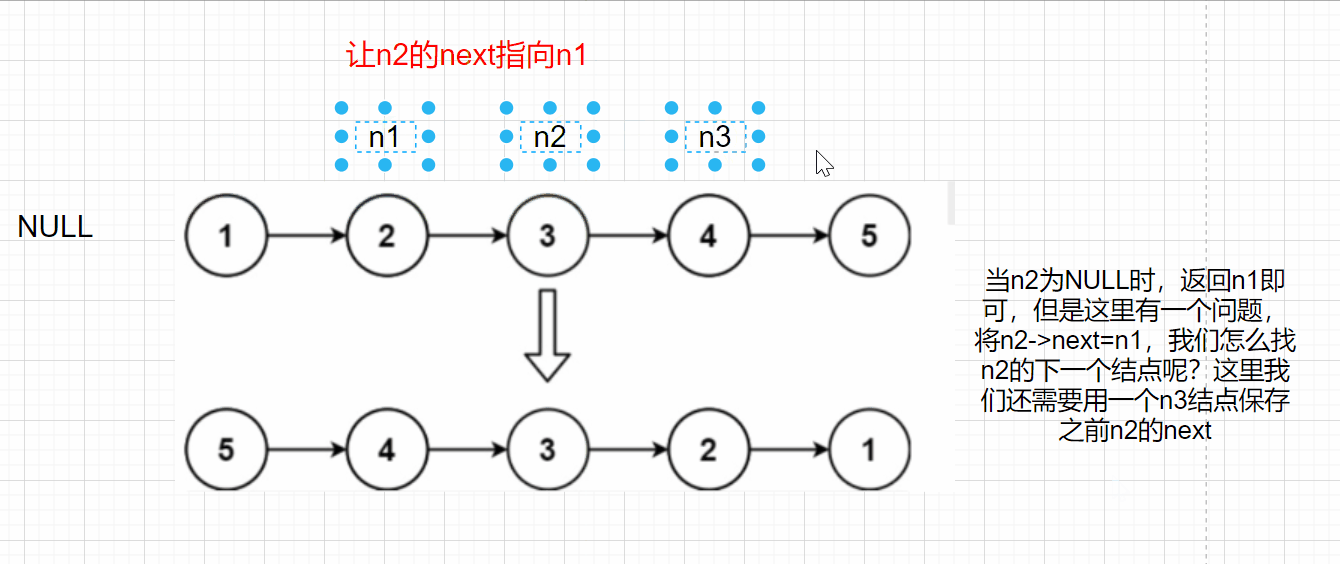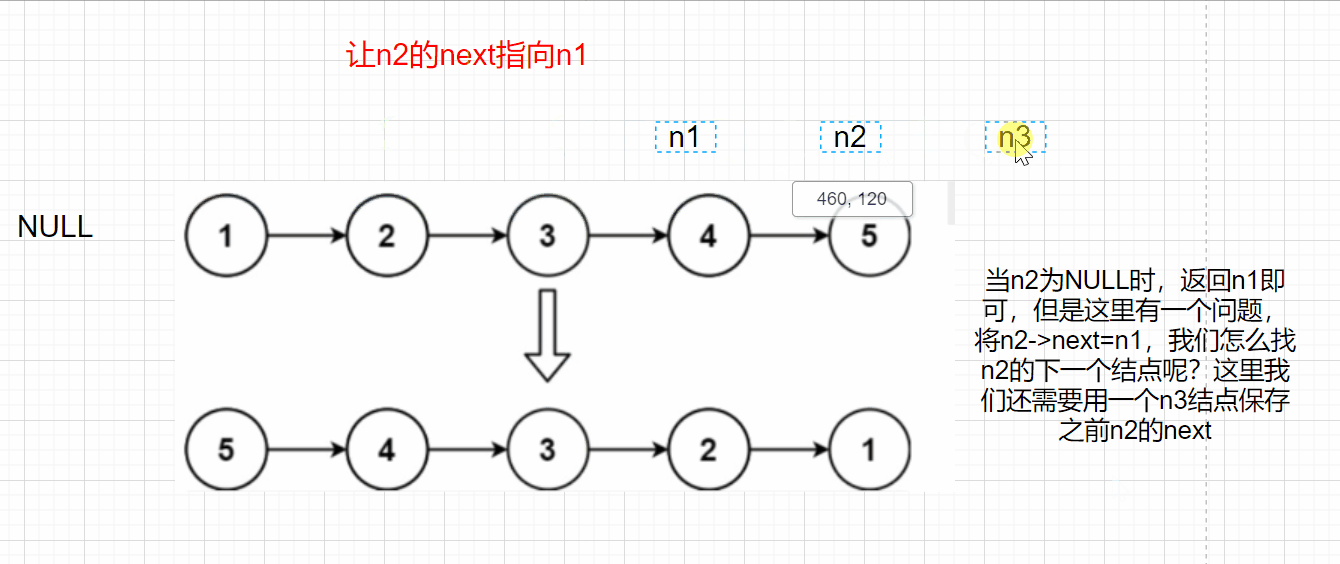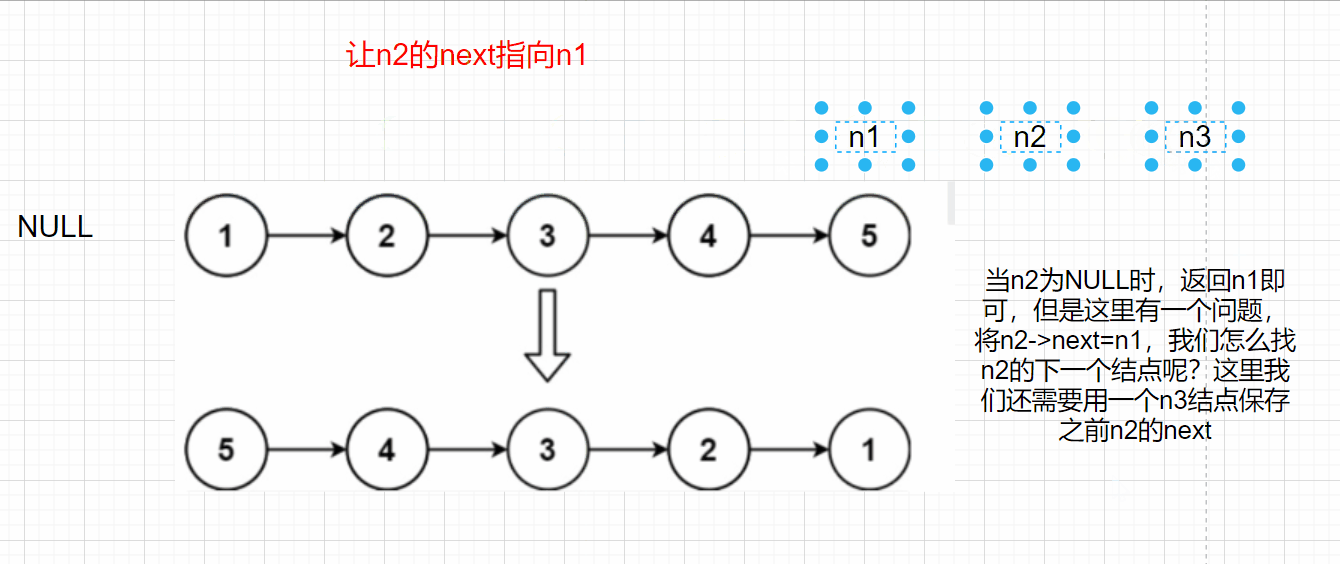
struct ListNode* reverseList(struct ListNode* head)
{
if(head==NULL)
{
return NULL;
}
struct ListNode* n1,*n2,*n3;
n1=NULL;
n2=head;
n3=head->next;
while(n2)
{
n2->next=n1;
n1=n2;
n2=n3;
if(n3)//When n3 is NULL, n3 has no next
{
n3=n3->next;
}
}
return n1;
}
Idea 2:
Head interpolation method: define a new linked list, newhead=NULL, the original linked list defines cur and next, and next records the next node of cur
struct ListNode* reverseList(struct ListNode* head)
{
if(head==NULL)
{
return NULL;
}
struct ListNode* cur=head;
struct ListNode* newhead=NULL;
struct ListNode* next=cur->next;
while(cur)
{
next=cur->next;
cur->next=newhead;
newhead=cur;
cur=next;
}
return newhead;
}
3. Find the middle node of a linked list
Title Description:
Given a non empty single linked list with head node, return the intermediate node of the linked list.
If there are two intermediate nodes, the second intermediate node is returned.
Example 1:
Input: [1,2,3,4,5]
Output: node 3 in this list (serialized form: [3,4,5])
The returned node value is 3.
Example 2:
Input: [1,2,3,4,5,6]
Output: node 4 in this list (serialized form: [4,5,6])
Since the list has two intermediate nodes with values of 3 and 4, we return the second node.
Title Source: Find the middle node of a linked list
Idea:
Using fast and slow pointers
slow one step at a time
fast takes two steps at a time
When fast comes to the end, slow comes to the middle node
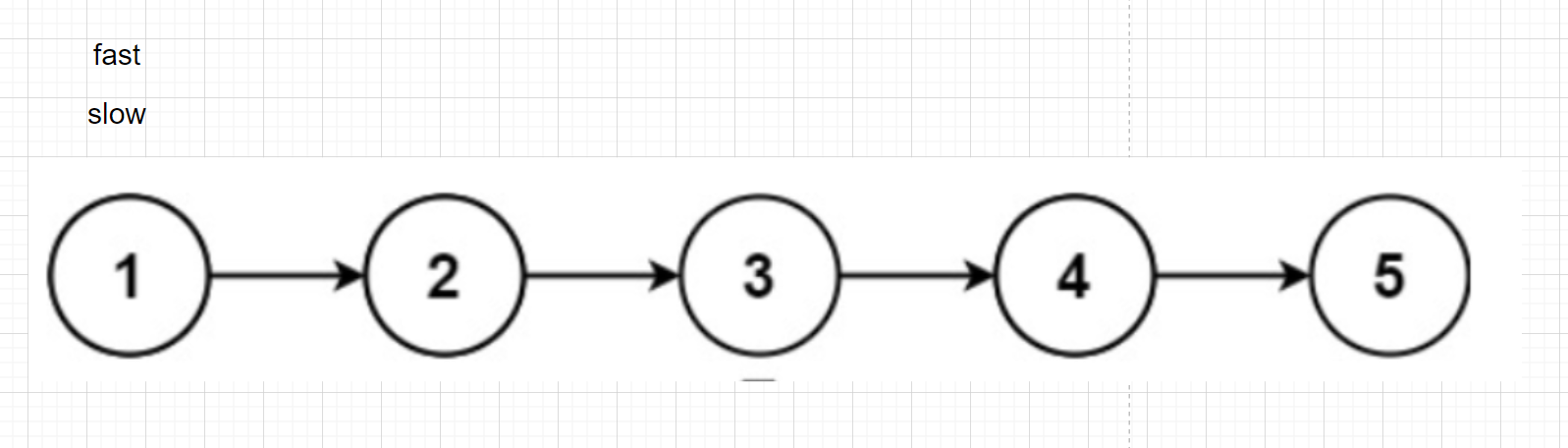
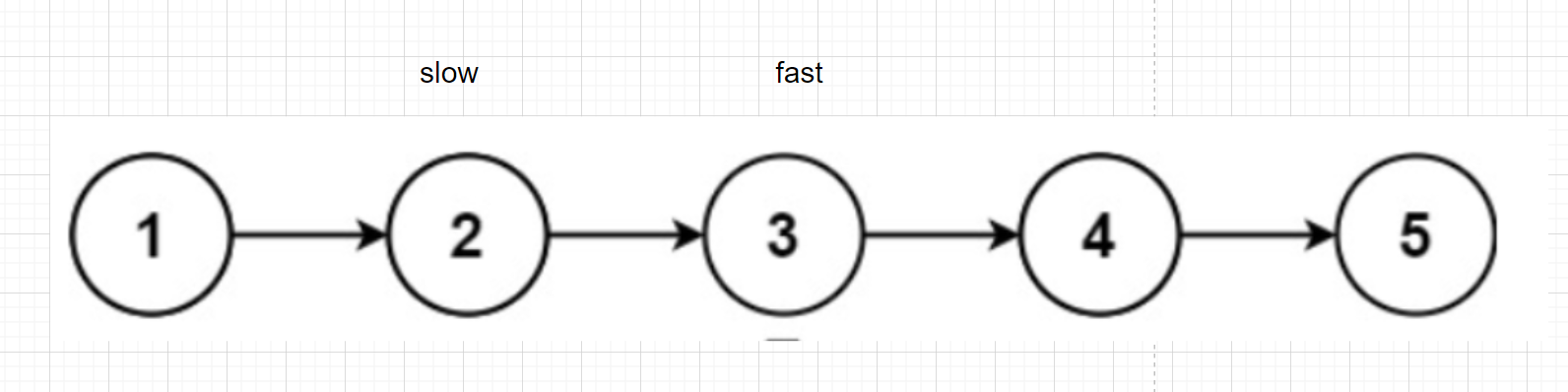
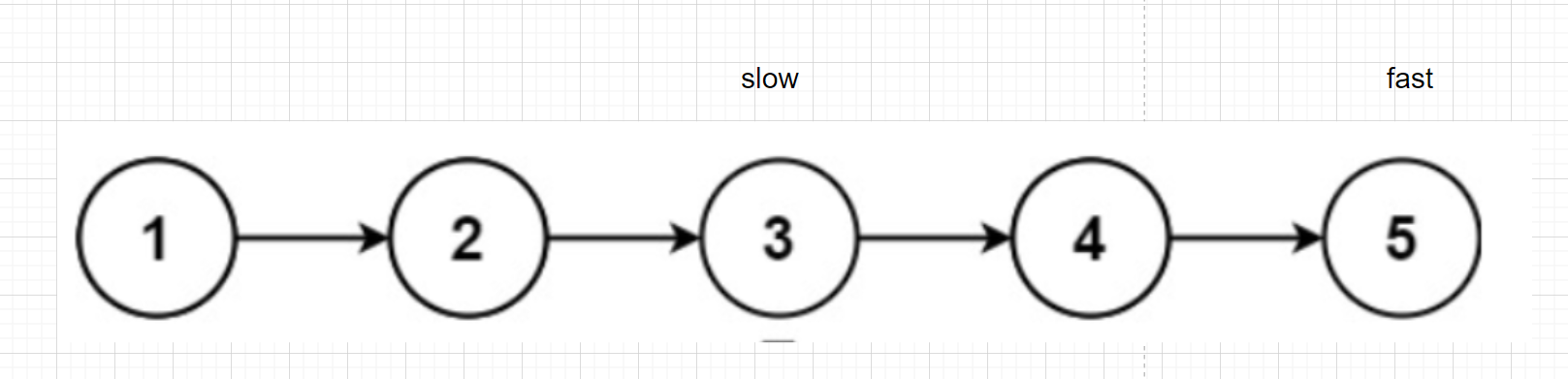
Slow takes one step at a time and fast takes two steps at a time. When fast comes to the end, slow goes to the middle node
But what about the even number of nodes? The requirement of the topic is to return: if there are two intermediate nodes, return the second intermediate node.
After drawing and understanding, it is found that:

When fast reaches NULL, slow reaches the second intermediate node.
Therefore, the condition for loop termination should be that fast is not NULL and fast - > next is not NULL
The problem solving code is as follows:
struct ListNode* middleNode(struct ListNode* head)
{
if(head==NULL)
{
return NULL;
}
//Speed pointer
struct ListNode* slow=head;
struct ListNode* fast=head;
while(fast&&fast->next!=NULL)
{
slow=slow->next;
fast=fast->next->next;
}
return slow;
}
4. The penultimate node in the lin k ed list
Title Description:
Input a linked list and output the penultimate node in the linked list.
Example 1
Input:
1,{1,2,3,4,5}
Return value:
{5}
Title Source: Find the middle node of a linked list
Idea:
Like the above question, we first define two pointers slow, fast, fast, take step k first, and then go together. Let's look at the following dynamic diagram:
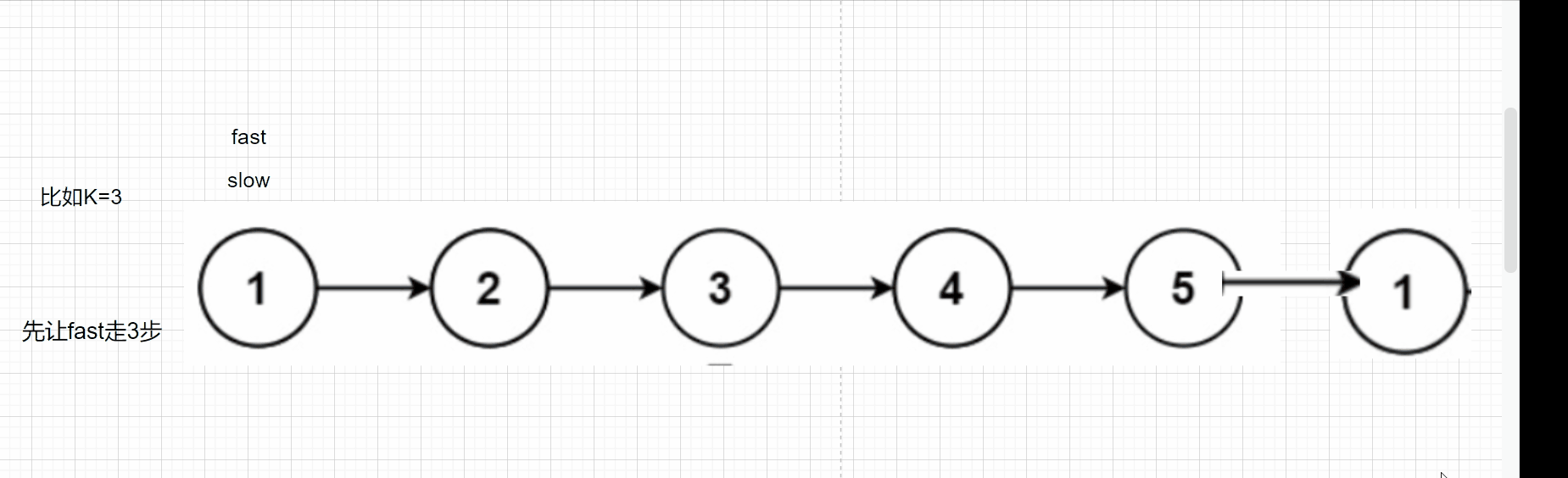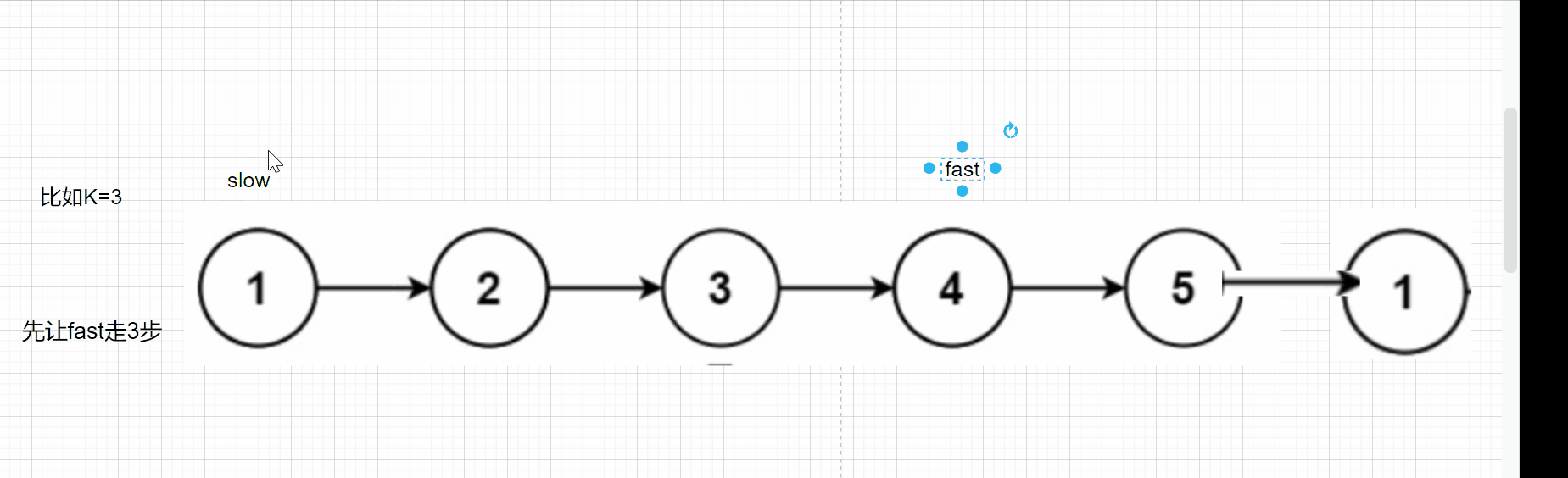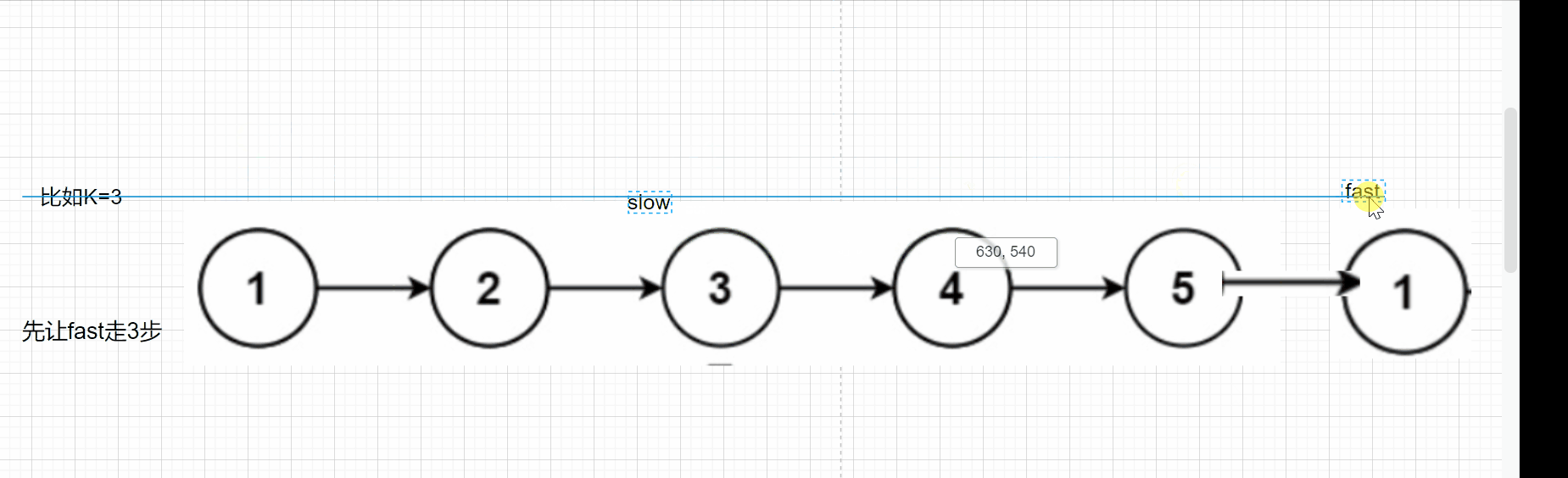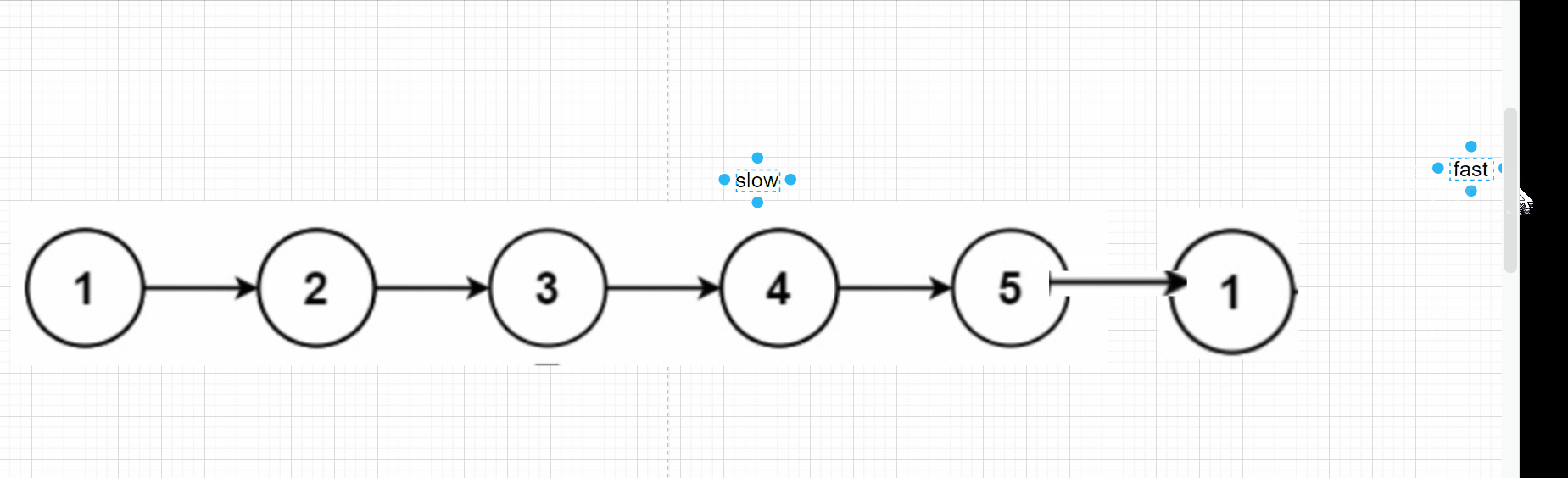
When fast is NULL, the slow is the penultimate node
It should be noted that if the input k is greater than the number of nodes, fast will become NULL before K steps are completed. In particular, NULL should be returned here
struct ListNode* FindKthToTail(struct ListNode* pListHead, int k )
{
if(k==0)
{
return NULL;
}
struct ListNode*slow,*fast;
slow=fast=pListHead;
//fast k steps first
while(k--)
{
if(fast==NULL)//The input k is greater than the number of nodes, and fast becomes NULL before it has finished K steps
{
return NULL;
}
fast=fast->next;
}
while(fast)
{
slow=slow->next;
fast=fast->next;
}
return slow;
}
When fast takes K steps first, if the input k is greater than the number of nodes, fast will become NULL before it has finished K steps. Here, it is necessary to judge whether fast is equal to NULL. If it is equal to NULL, it will directly return NULL.
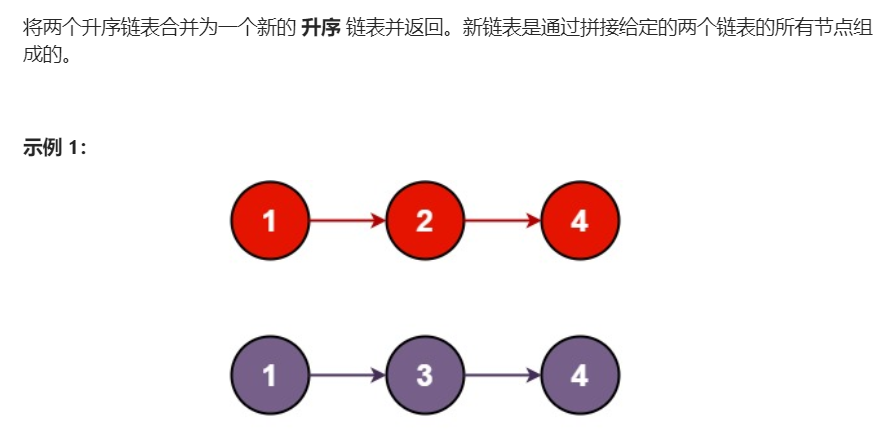
5. Merge two ordered linked lists
Title Description:
Merge the two ascending linked lists into a new ascending linked list and return. The new linked list is composed of all nodes of a given two linked lists.
Idea: take a small node and insert it into the new linked list
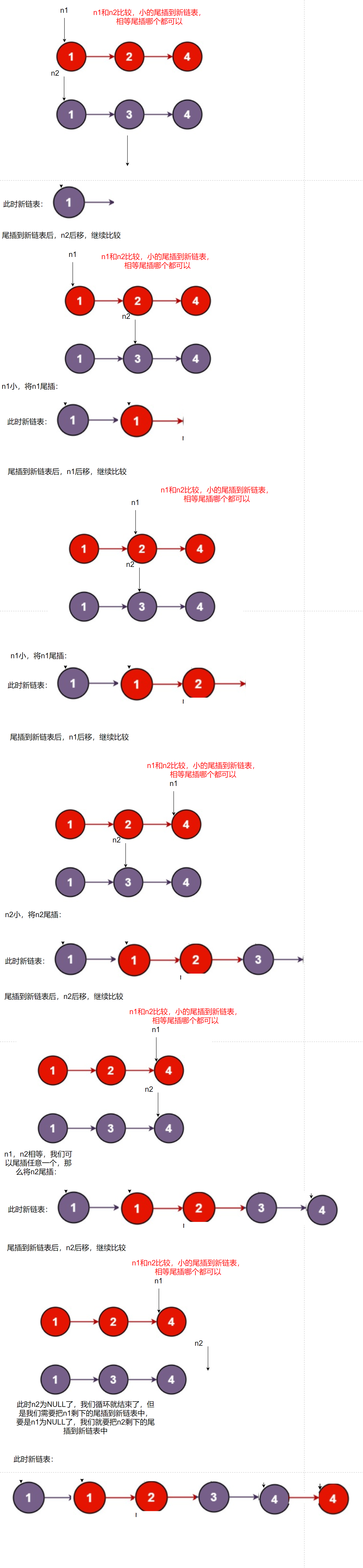
According to the analysis, our code is as follows:
struct ListNode* mergeTwoLists(struct ListNode* l1, struct ListNode* l2)
{
//If l1 is NULL, l2 is returned
if(l1==NULL)
{
return l2;
}
//If l2 is NULL, l1 is returned
if(l2==NULL)
{
return l1;
}
struct ListNode*newhead=NULL;//Head node of the new linked list
struct ListNode*tail=NULL;//Record the end of the new linked list
struct ListNode* n1=l1;
struct ListNode* n2=l2;
while(n1&&n2)
{
//Compare the val of n1 and n2 and insert the small tail in the new linked list
if(n1->val<n2->val)
{
//When the new linked list is NULL, that is, when there are no nodes
if(tail==NULL)
{
newhead=tail=n1;
}
//When it is not NULL, there are nodes
else
{
tail->next=n1;
tail=n1;
}
n1=n1->next;//At this time, the smaller tail has been inserted into the new linked list, and the iteration is carried out here
}
else
{
if(tail==NULL)
{
newhead=tail=n2;
}
else
{
tail->next=n2;
tail=n2;
}
n2=n2->next;
}
//Ends when n1 or n2 is NULL
}
//Link the remaining nodes that are not NULL to the tail of the new linked list
if(n1)
{
tail->next=n1;
}
if(n2)
{
tail->next=n2;
}
return newhead;
}
So can we optimize it?
Since we need special treatment when inserting n1 or n2 into a new linked list for the first time, we can insert a node into it outside first. There is no need to recycle it here. The tail insertion when there is no node should be considered in if and else. The code is as follows:
struct ListNode* mergeTwoLists(struct ListNode* l1, struct ListNode* l2)
{
if(l1==NULL)
{
return l2;
}
if(l2==NULL)
{
return l1;
}
struct ListNode*newhead=NULL;
struct ListNode*tail=NULL;
struct ListNode* n1=l1;
struct ListNode* n2=l2;
if(n1->val<n2->val)
{
newhead=tail=n1;
n1=n1->next;
}
else
{
newhead=tail=n2;
n2=n2->next;
}
while(n1&&n2)
{
if(n1->val<n2->val)
{
//Tail insert n1
tail->next=n1;
tail=n1;
n1=n1->next;
}
else
{
//Tail insertion n2
tail->next=n2;
tail=n2;
n2=n2->next;
}
}
if(n1)
{
tail->next=n1;
}
if(n2)
{
tail->next=n2;
}
return newhead;
}
Another method does not need to consider the case that the new linked list is NULL during tail insertion, that is, we set a head node with sentry position. Let's introduce it below:
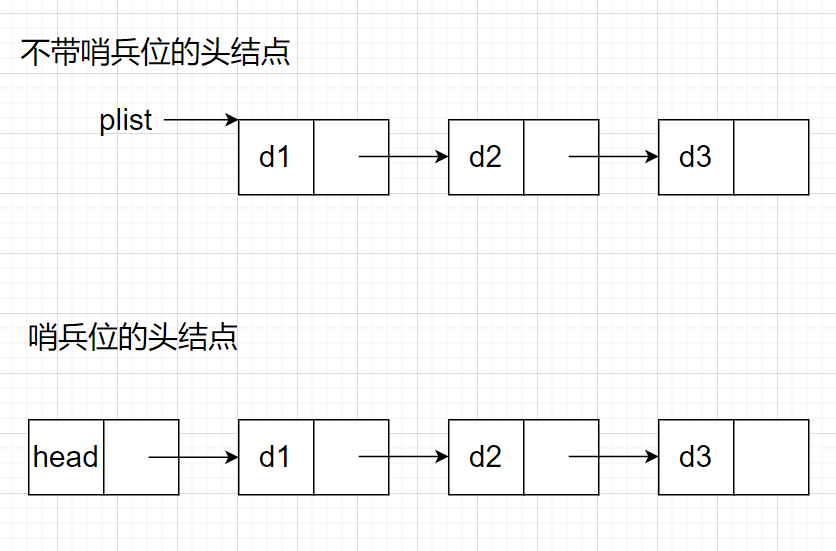
For the head node with sentinel bit, this node does not store valid data, and the function will never be modified to the pointer plist pointing to the first node storing valid data, because with this head node with sentinel bit, when inserting and deleting the first node in front of the first element node, its operation is unified with that of other nodes.
The head node with sentinel position looks a little simpler. Why doesn't our single linked list design this structure?
The structure of this head node rarely appears in practice, including hash bucket and adjacency table as substructures. Secondly, the linked list given in OJ basically does not take the lead.
Head node method with sentry position:
struct ListNode* mergeTwoLists(struct ListNode* l1, struct ListNode* l2)
{
if(l1==NULL)
{
return l2;
}
if(l2==NULL)
{
return l1;
}
struct ListNode*newhead=NULL;
struct ListNode*tail=NULL;
newhead=tail=(struct ListNode*)malloc(sizeof(struct ListNode));
while(l1&&l2)
{
if(l1->val<l2->val)
{
//Tail insert l1
tail->next=l1;
tail=l1;
l1=l1->next;
}
else
{
//Tail insertion l2
tail->next=l2;
tail=l2;
l2=l2->next;
}
}
if(l1)
{
tail->next=l1;
}
if(l2)
{
tail->next=l2;
}
//return newhead->next; Directly return this will cause a memory leak
struct ListNode* first = newhead->next;//Save the next of newhead first, and then save newhead free
free(newhead);
return first;
}
It should be noted that we need to release the opened head node with sentinel bit at last, otherwise there will be memory leakage. We need to return the next of newhead. Then we use first to save the next of newhead, and then free the newhead
6. Linked list segmentation
Title Description:
There is a header pointer ListNode pHead of a linked list. Given a certain value of X, write a piece of code to rank all nodes less than x before the other nodes, and the original data order cannot be changed. Return the header pointer of the rearranged linked list*
Idea:
1. Insert the tail smaller than x into a linked list
2. Insert the tail larger than x into a linked list
3. Then link the two linked lists together
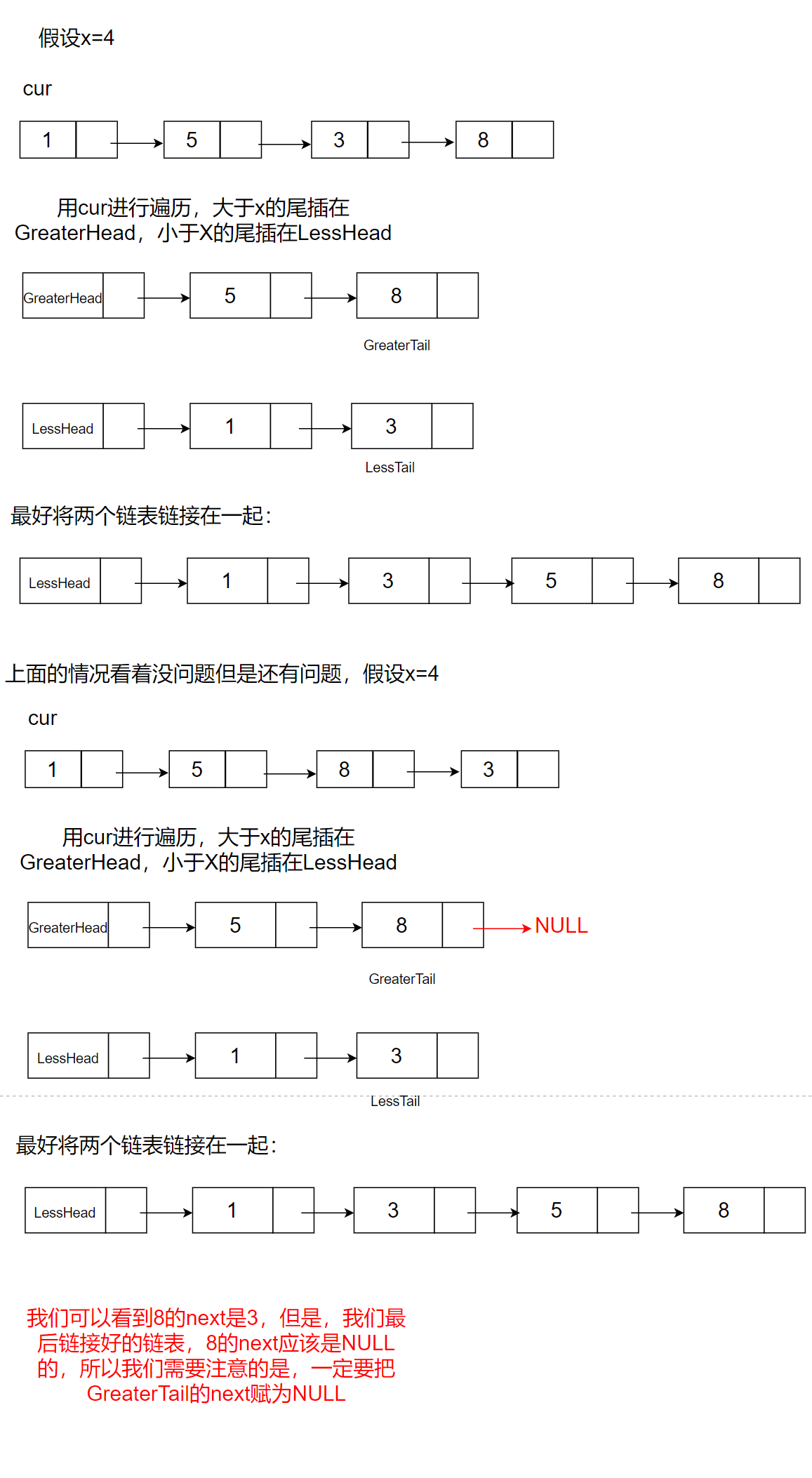
The code is as follows:
ListNode* partition(ListNode* pHead, int x)
{
// write code here
struct ListNode* LessHead=(struct ListNode*)malloc(sizeof(struct ListNode));//Small value node with sentinel position head
struct ListNode* GreaterHead=(struct ListNode*)malloc(sizeof(struct ListNode));//Node with sentinel position head with larger value
struct ListNode* LessTail=LessHead;
struct ListNode* GreaterTail=GreaterHead;
struct ListNode* cur = pHead;
while(cur)
{
if(cur->val<x)
{
//The tail is inserted into the linked list storing smaller values
LessTail->next=cur;
LessTail=cur;
}
else
{
//The tail is inserted into the linked list storing large values
GreaterTail->next=cur;
GreaterTail=cur;
}
cur=cur->next;
}
LessTail->next=GreaterHead->next;//link
GreaterTail->next=NULL;
struct ListNode* first=LessHead->next;
free(LessHead);
LessHead=NULL;
free(GreaterHead);
GreaterHead=NULL;
return first;
}
7. Palindrome structure of linked list
Title Description:
For a linked list, please design an algorithm with time complexity of O(n) and additional space complexity of O(1) to judge whether it is palindrome structure.
Given the header pointer A of A linked list, please return A bool value to represent whether it is A palindrome structure. Ensure that the length of the linked list is less than or equal to 900.
Test example:
1->2->2->1 return: true 1->2->3->2->1 return: true
Title Source: Palindrome structure of linked list
Idea 1:
Define an array, copy all val values in the linked list, and then compare whether the first and last are equal by subscript
bool chkPalindrome(ListNode* A) {
// write code here
int a[900];
struct ListNode* cur=A;
int n=0;
while(cur)
{
a[n++]=cur->val;
cur=cur->next;
}
int left=0;
int right=n-1;
while(left<right)
{
if(a[left]!=a[right])
{
return false;
}
left++;
right--;
}
return true;
}
The spatial complexity of this solution is O(n), and the spatial complexity does not meet the requirements, but niuke.com has given it. Some OJ problems have the requirements of time complexity and spatial complexity, but the inspection of background test cases is not easy to check the time complexity and spatial complexity. For the complexity, the OJ system is usually not very strict. This piece of leetcode will be stricter and more loose, including the integrity of test cases.
Let's look at a correct solution:
Idea 2:
1. Find the intermediate node first
2. Reverse the second half
3. Compare the first half and the second half
We have talked about finding intermediate nodes and inverse linked lists before. The rest is to compare the first half and the second half
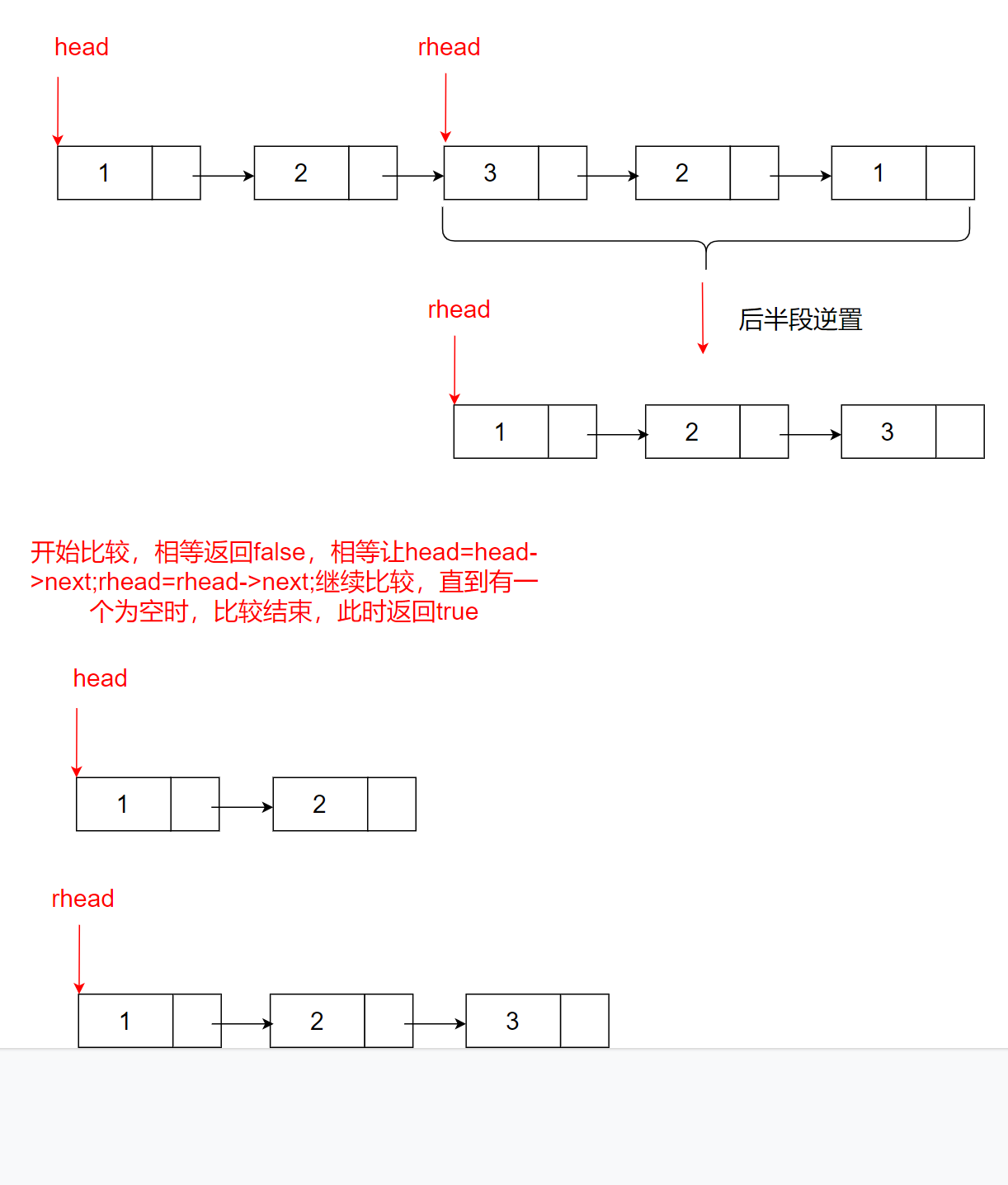
The code is as follows:
struct ListNode* FindMidNode(struct ListNode* phead)//Find intermediate node
{
struct ListNode*slow,fast;
slow=fast=phead;
while(fast&&fast->next)
{
slow=slow->next;
fast=fast->next;
}
return slow;
}
//Pass the first level pointer and return the header pointer with the return value
/*struct ListNode* reverseList(struct ListNode* phead)//Reverse linked list
{
struct ListNode*cur=phead;
struct ListNode*newhead=NULL;
while(cur)
{
struct ListNode*next=cur->next;
cur->next=newhead;
newhead=cur;
cur=next;
}
return newhead;
}*/
//Pass the secondary pointer and modify the header pointer in the function
void reverseList(struct ListNode** pphead)
{
struct ListNode*cur=pphead;
struct ListNode*newhead=NULL;
while(cur)//Head insertion inversion
{
struct ListNode*next=cur->next;
cur->next=newhead;
newhead=cur;
cur=next;
}
*pphead = newhead;
bool chkPalindrome(ListNode* A)
{
struct ListNode*mid = FindMidNode(A);
//struct ListNode*rHead = reverseList(mid);
struct ListNode*rhead=mid;
reverseList(&rhead);
struct ListNode*head=A;
while(rhead && head)
{
if(rhead->val!=head->val)
return false;
rhead=rhead->next;
head=head->next;
}
return true;
}
8. Intersection of linked lists
Title Description:
Here are the head nodes headA and headB of the two single linked lists. Please find and return the starting node where the two single linked lists intersect. If two linked lists have no intersection, null is returned.
As shown in the figure, two linked lists intersect at node c1:
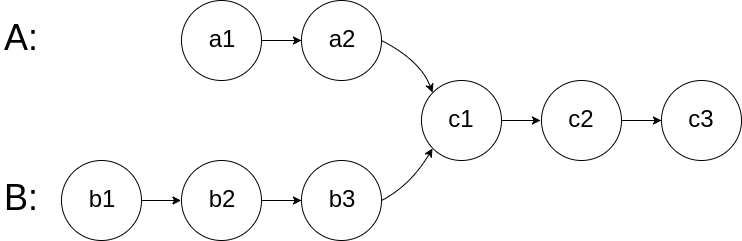
The title data ensures that there are no rings in the whole chain structure.
Note that after the function returns the result, the linked list must maintain its original structure.
Title Source: Intersection of linked lists
How to determine whether A and B linked lists intersect?
Idea 1:
Conventional idea: each node of A linked list is compared with all nodes of b linked list in turn. If there is an equal node, it is the intersection. The time complexity is O(N^2)
Optimization idea: calculate the length of A and B, lenA and lenB respectively, let the long one take the "lenA lenB" step first, and then compare to find the intersection. The time complexity is O(N)
Idea 2: judge whether the last node is the same
The problem requires us to return to the intersecting nodes, so we use the optimization idea of idea 1 to solve the problem:
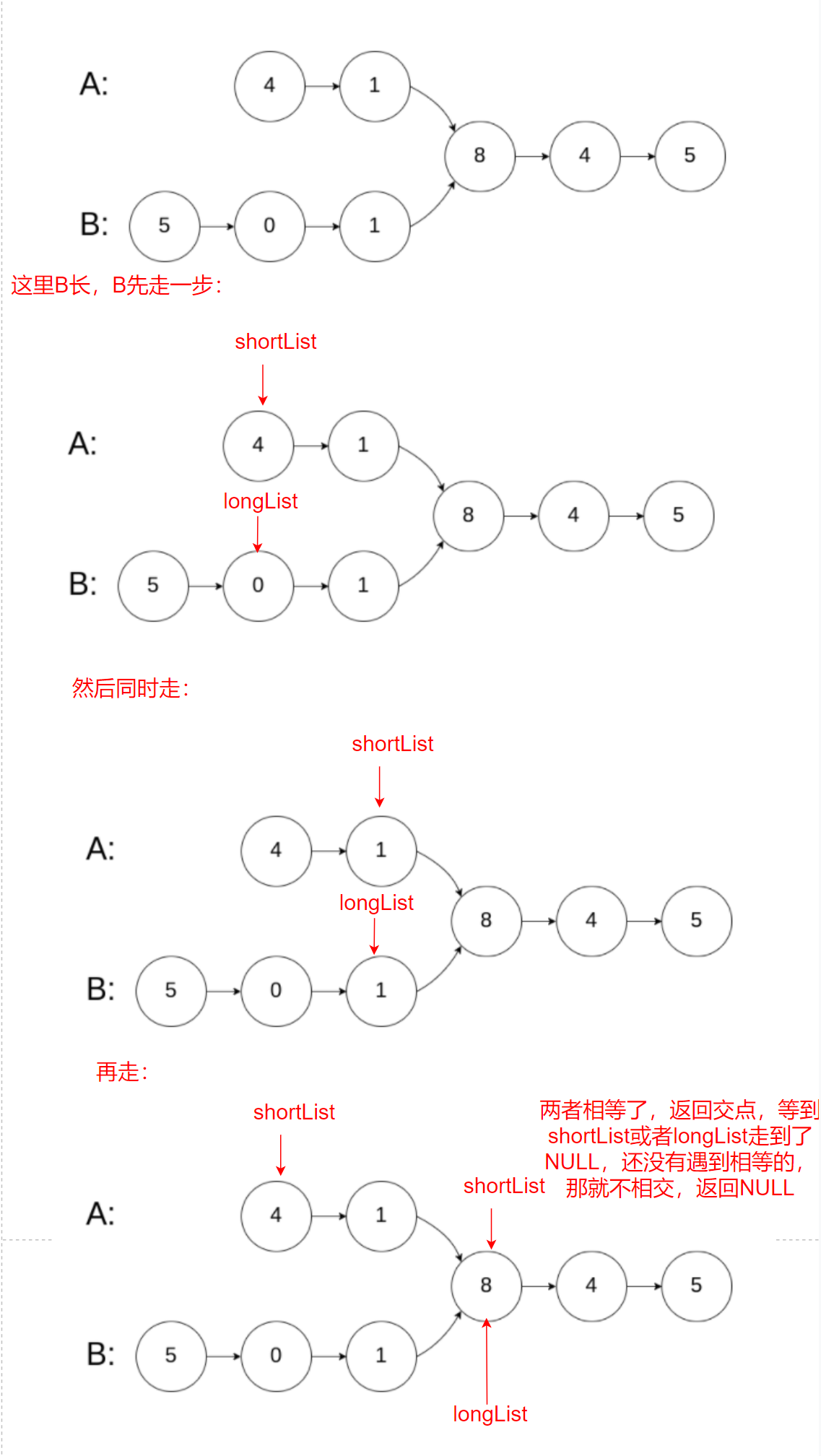
The code is as follows:
struct ListNode *getIntersectionNode(struct ListNode *headA, struct ListNode *headB) {
struct ListNode *curA = headA;
struct ListNode *curB = headB;
int lenB=0;
int lenA=0;
while(curA)//Calculate the length of A
{
lenA++;
curA=curA->next;
}
while(curB)//Calculate the length of B
{
lenB++;
curB=curB->next;
}
//Suppose A is long and B is short
struct ListNode *longList=headA;
struct ListNode *shortList=headB;
if(lenA<lenB)
{
longList=headB;
shortList=headA;
}
//Let the long take the first step
int gap=abs(lenA-lenB);
while(gap--)
{
longList=longList->next;
}
//Go at the same time and find the intersection
while(longList && shortList)
{
if(longList == shortList)
{
return longList;//Found return
}
longList=longList->next;
shortList=shortList->next;
}
//Indicates disjoint
return NULL;
}
First, we calculate the length of A and B linked lists. Then we assume that the long linked list is A and the short one is B. then, if Lena < lenb, we assign B to the long linked list and A to the short linked list. Then we let the long ones go first, and finally go together, and then find the intersection
9. Circular linked list
Problem Description:
Given a linked list, judge whether there are links in the linked list.
If there is a node in the linked list that can be reached again by continuously tracking the next pointer, there is a ring in the linked list. In order to represent the rings in a given linked list, we use the integer pos to represent the position where the tail of the linked list is connected to the linked list (the index starts from 0). If pos is - 1, there are no rings in the linked list. Note: pos is not passed as a parameter, but only to identify the actual situation of the linked list.
Returns true if there are links in the linked list. Otherwise, false is returned.
Advanced:
Can you solve this problem with O(1) (i.e., constant) memory?
Example 1:
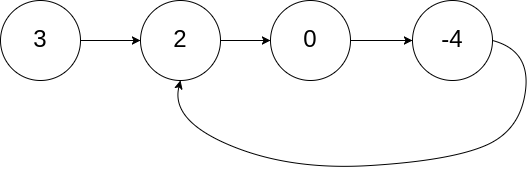
Input: head = [3,2,0,-4], pos = 1 Output: true Explanation: there is a ring in the linked list, and its tail is connected to the second node.
Example 2:
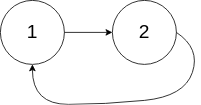
Input: head = [1,2], pos = 0 Output: true Explanation: there is a ring in the linked list, and its tail is connected to the first node.
Example 3:

Input: head = [1], pos = -1 Output: false Explanation: there are no links in the linked list.
Title Source: Circular linked list
Idea:
Fast and slow pointer, slow pointer takes one step at a time. The fast pointer takes two steps at a time. If the fast pointer can be equal to the slow pointer, it is a circular linked list, otherwise it is not
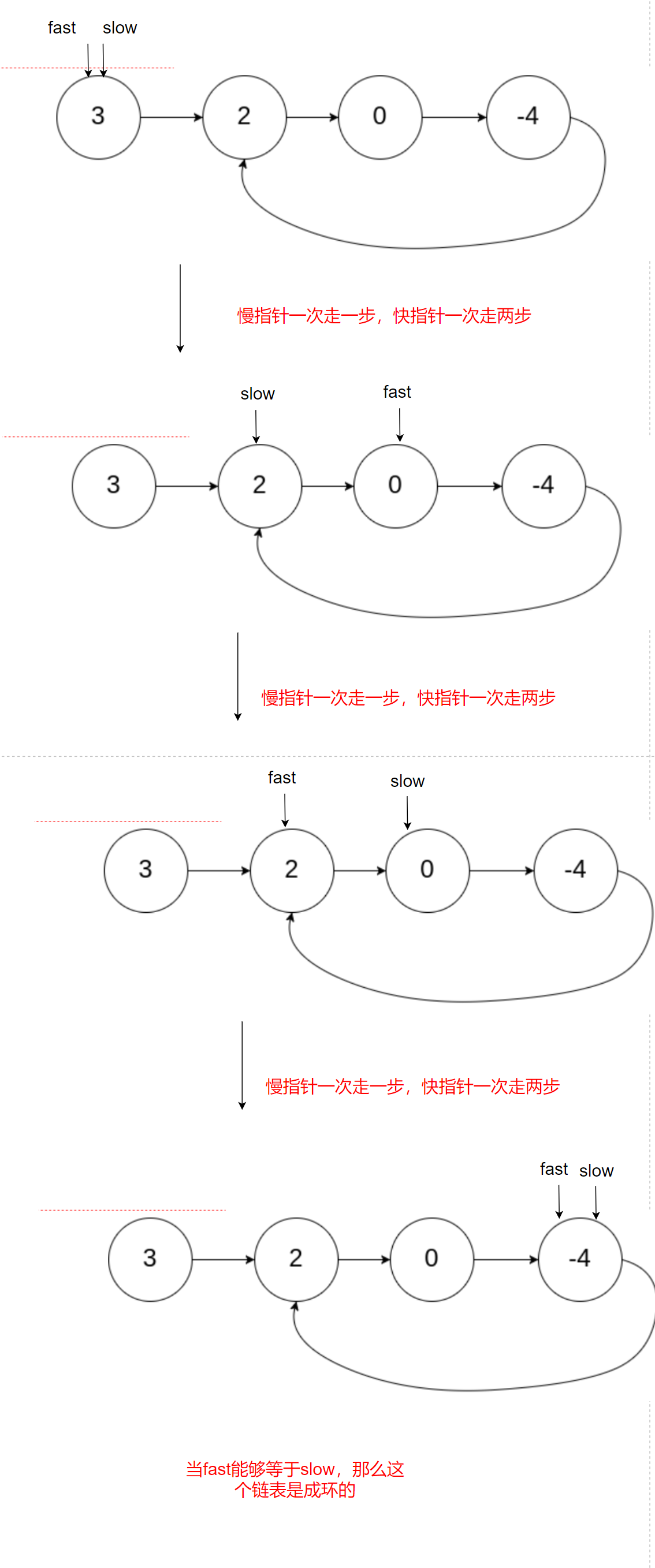
The code is as follows:
bool hasCycle(struct ListNode *head) {
struct ListNode *slow,*fast;
slow=fast=head;
while(fast && fast->next)
{
slow=slow->next;
fast=fast->next->next;
if(slow==fast)
{
return true;
}
}
return false;
}
The code of this question is very simple, but the examination of this question in the interview may not only let you write the code, but the interviewer may ask:
Interview questions:
- slow one step at a time, fast two steps at a time? Can we catch up? Please prove that:
answer:
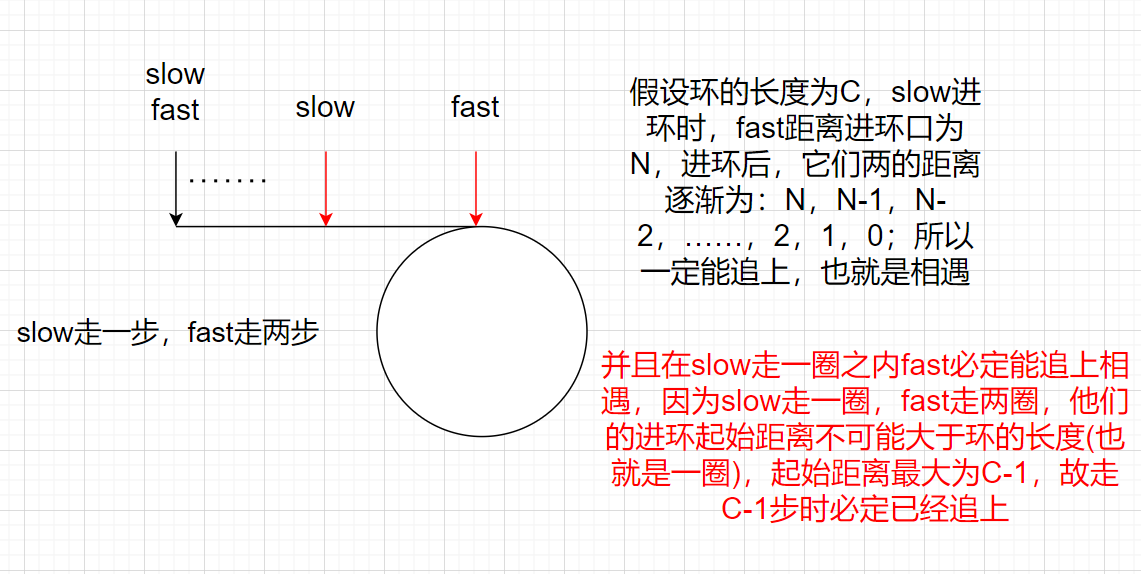
It must be possible to catch up. When slow enters the ring, fast has walked a certain length in the ring, and then a chase is formed in the ring. Fast goes to catch up with slow. Suppose that when slow enters the ring, the distance between fast and slow is N and the size of the ring is C, then N must be less than C
In catching up, slow takes one step at a time and fast takes two steps at a time
The distance change between fast and slow is:
N,N-1,N-2,N-3...2,1,0
N must be reduced to 0 at last, so if the distance is 0, it must meet
Slow enters the ring. Within one circle, fast will catch up with slow
- slow takes one step at a time, fast takes n steps at a time, n > (2,3,4,5...), OK? Firstly, the size of the ring and the length in front of the ring are uncertain. Please prove that:
answer:
Not necessarily catch up
Suppose slow takes one step at a time and fast takes three steps at a time. When slow enters the loop, the gap between them is N and the length of the loop is C
The distance between fast and slow varies as follows:
N,N-2,N-4,...,
When the distance between slow and fast is 0, it will catch up, so it means that N is an even number, and it will catch up
If N is an odd number and C-1 is an odd number, it will never catch up
When fast reaches the distance of - 1, their distance is C-1. When C-1 is also an odd number, they will never catch up
Conclusion: it's OK for fast to take x steps at a time and slow to take y steps at a time. The most important thing is that if the step difference in the process of catching up is x-y and the step difference is 1, we can catch up with others
10. Circular linked list II
Title Description:
Given a linked list, return the first node from the linked list into the ring. If the linked list is acyclic, null is returned.
In order to represent the rings in a given list, we use the integer pos to represent the position where the tail of the list is connected to the list (the index starts from 0). If pos is - 1, there is no ring in the list. Note that pos is only used to identify the ring and will not be passed to the function as a parameter.
Note: it is not allowed to modify the given linked list.
Advanced:
Can you use O(1) space to solve this problem?
Title Source: Circular linked list II
Solution idea 1:
One pointer starts from the meeting point and the other pointer starts from the head. They will meet at the entry point
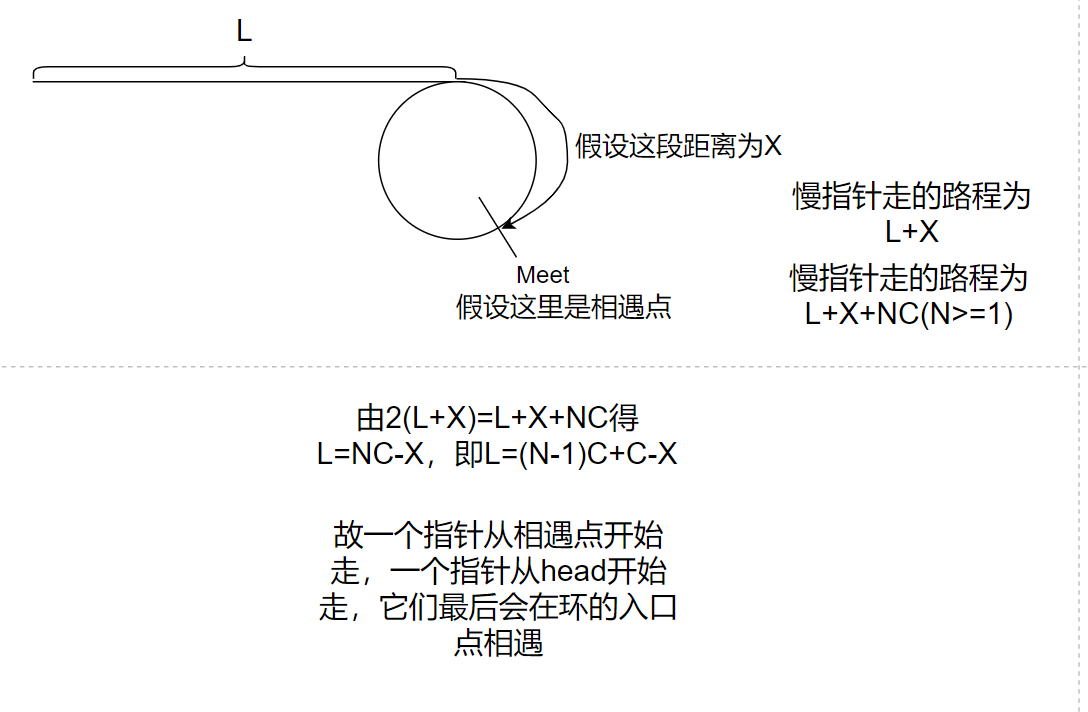
prove:
Suppose: the distance from the chain header to the entry point is L, the distance from the encounter point to the entry point is X, and the length of the ring is C,
The distance of the slow pointer is L+X
The fast pointer goes L+C+X
2(L+X)=L+C+X, L=C-X*
The proof of many articles is this, but this proof is wrong, because fast does not necessarily walk only once in the ring before slow enters the ring
Correct proof
When meeting: the distance taken by the slow pointer is L+X
Fast pointer distance L+NC+X (n > = 1)
2(L+X)=L+NC+X
L+X=NC
L=NC-X
L=(N-1)C+C-X
Conclusion: a pointer starts from the meeting point and a pointer starts from the head. They will meet at the entry point
Problem solving idea 2:
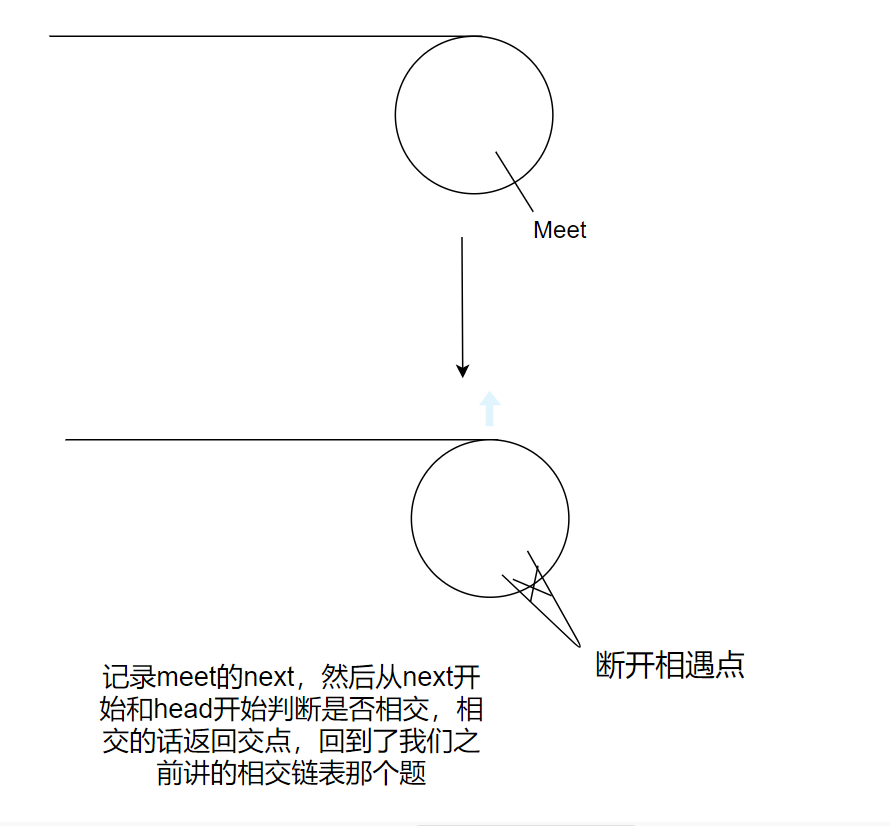
Break the meet point, then judge the intersection and return to the intersection
The code is as follows:
struct ListNode* getIntersectionNode(struct ListNode* headA, struct ListNode* headB) {
//1. Calculate the length of A and B
struct ListNode*curA = headA;
struct ListNode*curB = headB;
int lenA=0;
int lenB=0;
while(curA)
{
lenA++;
curA=curA->next;
}
while(curB)
{
lenB++;
curB=curB->next;
}
//2. Calculate the length difference, and take the difference step first
int gap = abs(lenA-lenB);
struct ListNode* longList = headA;
struct ListNode* shortList = headB;
if(lenA<lenB)
{
longList = headB;
shortList = headA;
}
while(gap--)
{
longList=longList->next;
}
//3. Then go together
while(longList && shortList)
{
if(longList==shortList)
{
return longList;
}
longList=longList->next;
shortList=shortList->next;
}
return NULL;
}
struct ListNode *detectCycle(struct ListNode *head) {
struct ListNode *slow=head;
struct ListNode *fast=head;
while(fast &&fast->next)
{
slow=slow->next;
fast=fast->next->next;
if(slow==fast)
{
//Met
struct ListNode *meet=slow;
struct ListNode *next=meet->next;//Record the next node at the meeting point
meet->next=NULL;//Disconnect the meeting point
return getIntersectionNode(head,next);
}
}
return NULL;
}
Record the next of the meet, and then judge whether it intersects from the next and head. If it intersects, return to the intersection and return to the problem of intersection linked list we talked about before
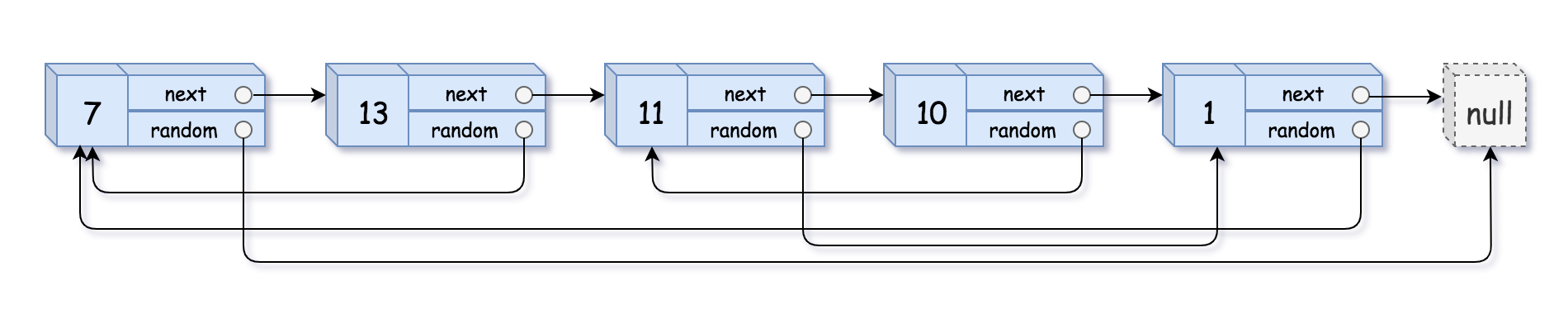
11. Copy the linked list with random pointer
Title Description:
Give you a linked list with a length of n. each node contains an additional random pointer random, which can point to any node or empty node in the linked list.
Construct a deep copy of this linked list. The deep copy should consist of exactly n new nodes, in which the value of each new node is set to the value of its corresponding original node. The next pointer and random pointer of the new node should also point to the new node in the replication linked list, and these pointers in the original linked list and the replication linked list can represent the same linked list state. The pointer in the copy linked list should not point to the node in the original linked list.
For example, if there are two nodes X and Y in the original linked list, where x.random -- > y. Then, the corresponding two nodes X and Y in the copy linked list also have x.random -- > y.
Returns the header node of the copy linked list.
Link: https://leetcode-cn.com/problems/copy-list-with-random-pointer
Example 1
Input: head = [[7,null],[13,0],[11,4],[10,2],[1,0]]
Output: [[7,null],[13,0],[11,4],[10,2],[1,0]]
Example 2:

Input: head = [[1,1],[2,1]]
Output: [[1,1], [2,1]]
Example 3:

Input: head = [[3,null],[3,0],[3,null]]
Output: [[3,null],[3,0],[3,null]]
Example 4:
Input: head = []
Output: []
Explanation: the given linked list is null (null pointer), so null is returned.
Title Source: Copy linked list with random pointer
Idea 1:
1. First copy each node of the original linked list and link the copied new nodes
2. Calculate the relative distance between the random and cur of each node in the original linked list
Then copy the node with the relative distance from the new linked list to the current node, assign it to random, find the random time complexity of each node is O(N), and N nodes are O(N^2) - low efficiency
Idea 2:
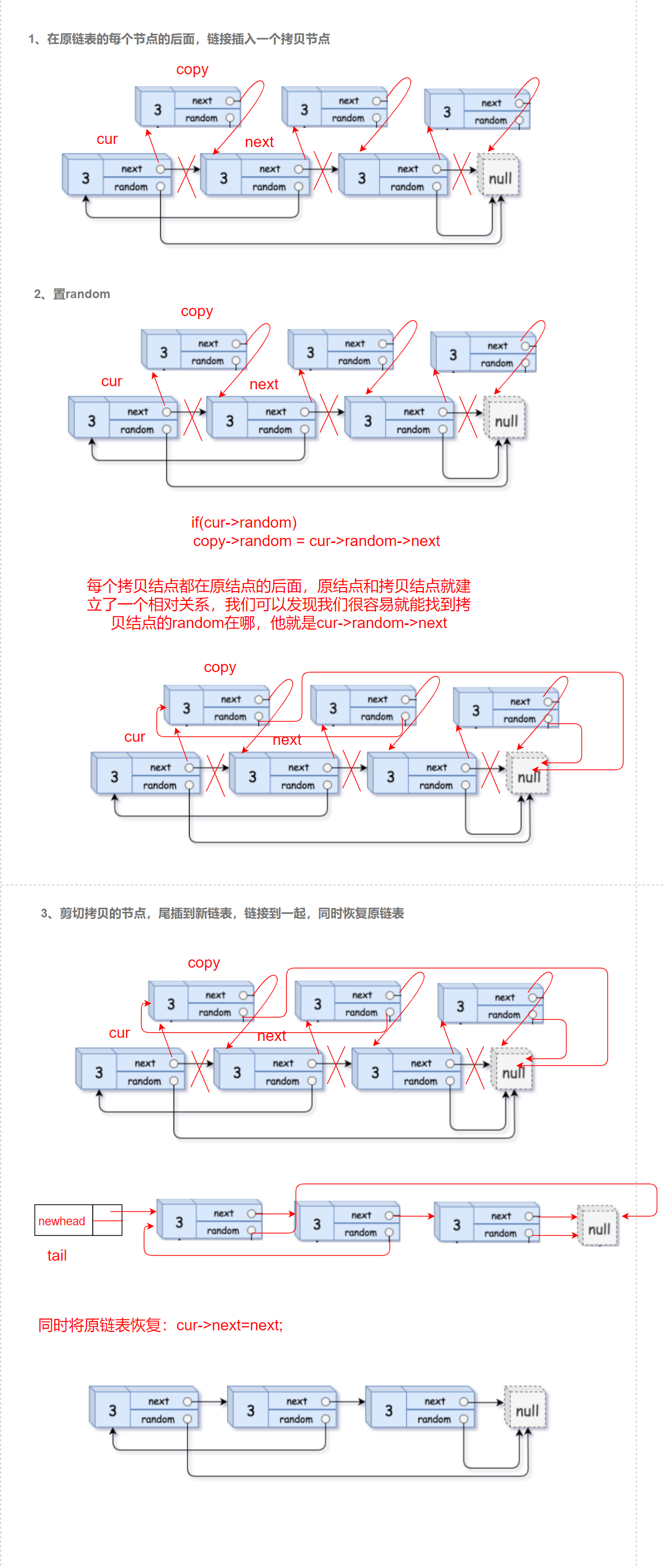
1. After each node of the original linked list, the link inserts a copy node
2. Set random
3. Cut out the copy nodes, link them together, and restore the original linked list at the same time
The code is as follows:
struct Node* copyRandomList(struct Node* head) {
if(head==NULL)
{
return NULL;
}
//1. The copy of each node is linked behind that node
struct Node* cur=head;
while(cur)
{
struct Node* next = cur->next;
struct Node* copy = (struct Node*)malloc(sizeof(struct Node));
copy->val=cur->val;
cur->next=copy;
copy->next=next;
cur=next;
}
//2. Set random
cur=head;
while(cur)
{
struct Node* copy=cur->next;
if(cur->random)
{
copy->random = cur->random->next;
}
else
{
copy->random=NULL;
}
cur=copy->next;
}
//3. Cut the copied node and insert the tail into the new linked list
cur=head;
struct Node* newhead,*tail;
newhead=tail=(struct Node*)malloc(sizeof(struct Node));
while(cur)
{
struct Node* copy=cur->next;
struct Node* next=copy->next;
tail->next=copy;
tail=copy;
cur->next=next;
cur=next;
}
struct Node* first=newhead->next;
free(newhead);
newhead=NULL;
return first;
}
Linking the copy of each node behind the node is equivalent to the insertion operation in the linked list. Each copy node is behind the original node, and a relative relationship is established between the original node and the copy node. We can find that we can easily find out where the random of the copy node is, cur - > Random - > next, and then set the copied node random through the relative position, Finally, insert the end of the copied node into the new linked list. Here, we use the head node with sentinel bit for the new linked list.
The above is the explanation of the blogger's popular OJ on complexity, array and linked list. We look forward to your praise! Welcome to study and discuss. If there are any mistakes, I hope you can leave a message in the comment area.