Eight queens
At 8 × Eight queens are placed on the 8-grid chess so that they can't attack each other, that is, any two Queens can't be in the same row, column or slash. How many kinds of placement methods are there?
Source code
public class Demo {
static int TRUE = 1, FALSE = 0, EIGHT = 8;
static int[] queen = new int[EIGHT];
static int number = 0;
static int count=0;
//Constructor
public Demo() {
number = 0;
}
public static void print1(){
count++;
for(int i=0;i<EIGHT;i++){
System.out.print(queen[i]+" ");
}
System.out.println();
}
//Judge whether the queen on (row, col) is attacked
public static boolean attack(int row) {
for(int i=0;i<row;i++){
if(queen[i]==queen[row]||Math.abs(i-row)==Math.abs(queen[i]-queen[row])){
return false;
}
}
return true;
}
//Locate the queen
public static void thePlace(int row){
if(row==EIGHT){
print1();
print2();
return;
}
for(int i=0;i<EIGHT;i++){
queen[row]=i;
if(attack(row))
thePlace(row+1);
}
}
public static void main(String[] args){
thePlace(0);
System.out.println(count);
}
}
Graphic analysis second understand source code
static int[] queen = new int[EIGHT];
Note: in the source code, row represents the number of lines. Please imagine a chessboard. Here, a one-dimensional array queen[EIGHT] is defined; The subscript of each source number of one-dimensional array is used as the row number, and the value in the array corresponding to the subscript is used as the column number. Therefore, each element in each printed dimension and its corresponding subscript are the coordinates of all falling children in each case
public static boolean attack(int row) {
for(int i=0;i<row;i++){
if(queen[i]==queen[row]||Math.abs(i-row)==Math.abs(queen[i]-queen[row])){
return false;
}
}
return true;
}
The attack() method is used to judge whether there are other queens on the column number and diagonal corresponding to its location. If so, it will not enter recursion, otherwise, it will enter recursion,
Resolution:
Note that in the source code, the main function is at the bottom, only the place () method is called, and the incoming parameter is 0, that is, in this method, row (number of rows) is 0 first, and first judge whether row (number of rows) is equal to eight (eight); Not equal to. Go down to the for loop. Recursion is involved in the for loop. Pay attention to the following figure:
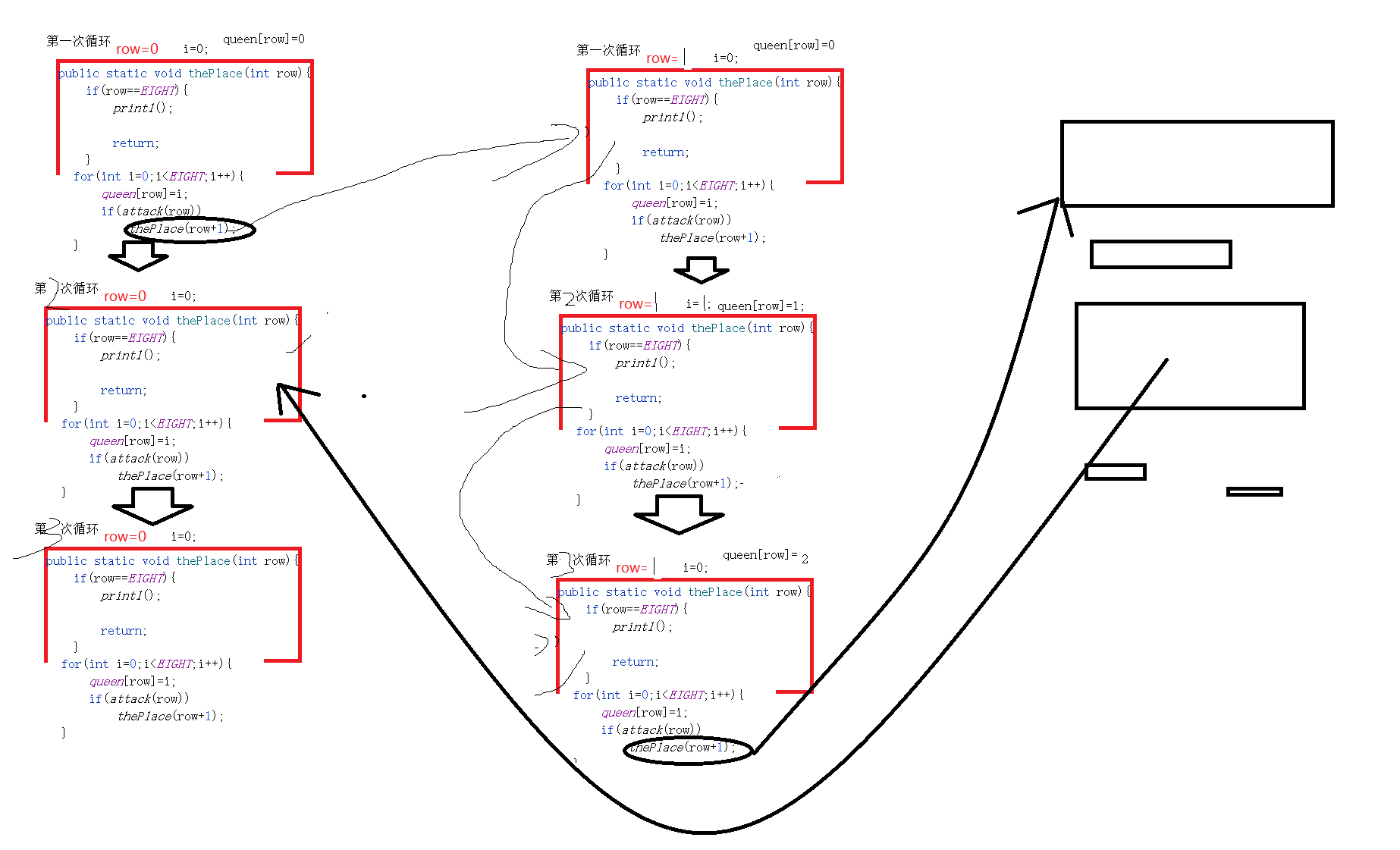
For the first time, if the chessboard is empty, it will fall directly into recursion.
Every time you enter recursion, you find a place where a column in a certain row can be placed. If it cannot be found, enter the for loop in the current recursion level until a place can be found. If the loop ends at the end, the for loop in the previous level of recursion is returned. If you keep cycling, you can count all the cases.
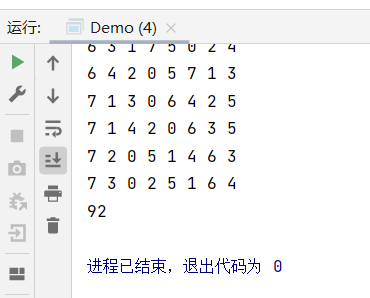
Further advanced: print out the chess chart of each situation
public static void print2(){
String[][] arr={{" "," "," "," "," "," "," "," "},
{" "," "," "," "," "," "," "," "},
{" "," "," "," "," "," "," "," "},
{" "," "," "," "," "," "," "," "},
{" "," "," "," "," "," "," "," "},
{" "," "," "," "," "," "," "," "},
{" "," "," "," "," "," "," "," "},
{" "," "," "," "," "," "," "," "}};
for(int i=0;i<EIGHT;i++){
arr[i][queen[i]]="*";
}
for(int i=0;i<EIGHT;i++){
for(int j=0;j<EIGHT;j++) {
if(j<EIGHT-1) {
System.out.print(" " + arr[i][j] + " ");
System.out.print("|");
}else{
System.out.print(" " + arr[i][j] + " ");
}
}
System.out.println();
if(i<EIGHT-1){
for (int k = 0; k < EIGHT; k++) {
if(k==7)
System.out.print("---");
else
System.out.print("---|");
}
}
System.out.println();
}
}
Overall code implementation
package Eight queens problem;
public class Demo {
static int TRUE = 1, FALSE = 0, EIGHT = 8;
static int[] queen = new int[EIGHT];
static int number = 0;
static int count=0;
//Constructor
public Demo() {
number = 0;
}
//Print one-dimensional array results
public static void print1(){
count++;
for(int i=0;i<EIGHT;i++){
System.out.print(queen[i]+" ");
}
System.out.println();
}
//Print checkerboard results
public static void print2(){
String[][] arr={{" "," "," "," "," "," "," "," "},
{" "," "," "," "," "," "," "," "},
{" "," "," "," "," "," "," "," "},
{" "," "," "," "," "," "," "," "},
{" "," "," "," "," "," "," "," "},
{" "," "," "," "," "," "," "," "},
{" "," "," "," "," "," "," "," "},
{" "," "," "," "," "," "," "," "}};
for(int i=0;i<EIGHT;i++){
arr[i][queen[i]]="*";
}
for(int i=0;i<EIGHT;i++){
for(int j=0;j<EIGHT;j++) {
if(j<EIGHT-1) {
System.out.print(" " + arr[i][j] + " ");
System.out.print("|");
}else{
System.out.print(" " + arr[i][j] + " ");
}
}
System.out.println();
if(i<EIGHT-1){
for (int k = 0; k < EIGHT; k++) {
if(k==7)
System.out.print("---");
else
System.out.print("---|");
}
}
System.out.println();
}
}
//Judge whether the queen on (row, col) is attacked
public static boolean attack(int row) {
for(int i=0;i<row;i++){
if(queen[i]==queen[row]||Math.abs(i-row)==Math.abs(queen[i]-queen[row])){
return false;
}
}
return true;
}
//Locate the queen
public static void thePlace(int row){
if(row==EIGHT){
print1();
print2();
return;
}
for(int i=0;i<EIGHT;i++){
queen[row]=i;
if(attack(row))
thePlace(row+1);
}
}
public static void main(String[] args){
thePlace(0);
System.out.println(count);
}
}

Hanoi
Tower of Hanoi: the tower of Hanoi comes from Indian legend. When Brahma created the world, he built three gold and steel pillars, one of which is stacked with 64 gold discs from the bottom up. Brahma ordered Brahman to rearrange the disk on another column in order of size from below. It is also stipulated that the disc cannot be enlarged on the small disc, and only one disc can be moved between the three columns at a time.
When the disc is n, how many times do you have to move it?
Source code
import java.util.Scanner;
public class Demo2 {
static int times;
public static void main(String[] args){
Scanner sc=new Scanner(System.in);
System.out.println("Please enter the number of plates");
int j=sc.nextInt();
hanoi(j,'A','B','C');
}
public static void move(int disk,char p1,char p3){
System.out.println("The first"+(++Demo2.times)+"Second general"+disk+"from"+p1+"Move to"+p3);
}
public static void hanoi(int n,char p1,char p2,char p3){
if(n==1) {
move(n,p1, p3);
}else{
//Move n-1 discs onto the B-pillar
hanoi(n-1,p1,p3,p2);
//Move the last disc onto the C-pillar
move(n,p1,p3);
//Move n-1 discs onto the C-pillar
hanoi(n-1,p2,p1,p3);
}
}
}
Graphic analysis seckill source code
The analysis is carried out with n=3.
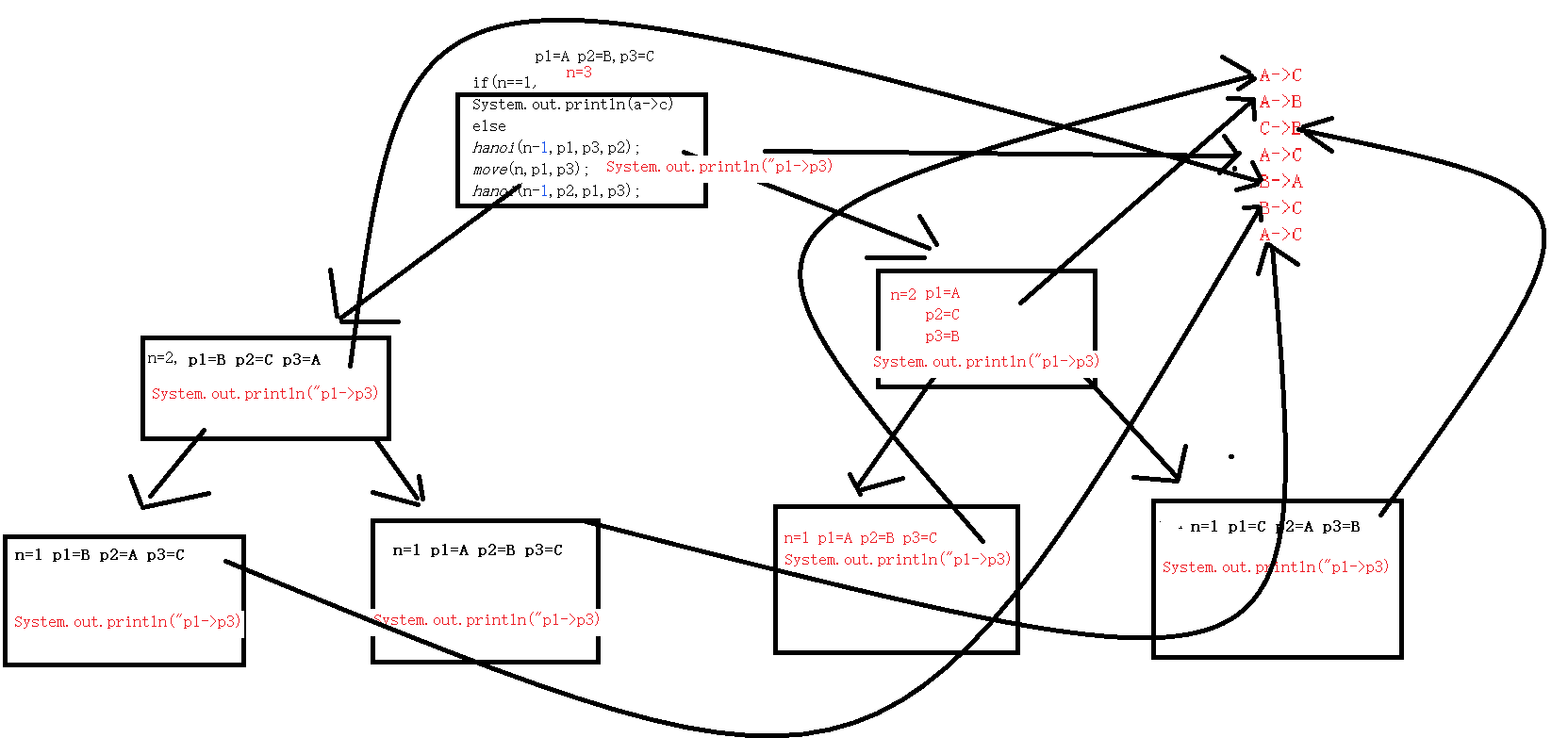
Maze problem in source code interpretation
There is a maze map, with some reachable positions and some unreachable positions (obstacles, walls, boundaries). From one position to the next can only be realized by taking one step up (or right, or down, or left). Starting from the starting point, how to find a path to the end point, and leave marks under the path.
First simulate a stack with a linked list:
public class Node {
int x;
int y;
Node next;
public Node(){}
public Node(int x,int y){
this.x =x;
this.y =y;
next=null;
}
}
public class NodeList {
Node first;
Node last;
//Stack pressing
public void push(int x,int y){
Node newNode=new Node(x,y);
if(first==null){
first=newNode;
last=newNode;
}else{
last.next=newNode;
last=newNode;
}
}
//Out of stack
public void pop(){
if(first==null){
System.out.println("Stack full, delete option by mistake");
return;
}else{
Node delNode=first;
while(delNode.next!=last)
delNode=delNode.next;
delNode.next=last.next;
last=delNode;
}
}
}
Operation stack problem solving
public class Demo {
public static int exitx=8;
public static int exity=10;
public static int[][] arr = {{1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1},
{1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1},
{1, 1, 1, 0, 1, 1, 0, 0, 0, 0, 1, 1},
{1, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 1},
{1, 1, 1, 0, 0, 0, 0, 1, 1, 0, 1, 1},
{1, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 1},
{1, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 1},
{1, 1, 1, 1, 1, 1, 0, 1, 1, 0, 1, 1},
{1, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1},
{1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1},
};
public static void main(String[] args) {
int x = 1;
int y = 1;
NodeList L = new NodeList();
System.out.println("Before the mouse goes");
for (int i = 0; i < 10; i++) {
for (int j = 0; j < 12; j++) {
System.out.print(arr[i][j] + " ");
}
System.out.println();
}
while (x <=exitx&&y<=exity){
arr[x][y]=2;
if(arr[x-1][y]==0){
x--;
L.push(x,y);
}else if(arr[x+1][y]==0){
x++;
L.push(x,y);
}else if(arr[x][y-1]==0){
y--;
L.push(x,y);
}else if(arr[x][y+1]==0){
y++;
L.push(x,y);
}else{
if(chkExit(x,y,exitx,exity)){
break;
}
else{
arr[x][y]=2;
L.pop();
x=L.last.x;
y=L.last.y;
}
}
}
System.out.println("After the mouse left");
for (int i = 0; i < 10; i++) {
for (int j = 0; j < 12; j++) {
System.out.print(arr[i][j] + " ");
}
System.out.println();
}
}
public static boolean chkExit(int x,int y,int exitx,int exity) {
if (x == exitx && y == exity) {
if(arr[x-1][y]==1||arr[x+1][y]==1||arr[x][y-1]==1||arr[x][y+1]==2){
return true;
}else if(arr[x-1][y]==1||arr[x+1][y]==1||arr[x][y-1]==2||arr[x][y+1]==1){
return true;
}else if(arr[x-1][y]==1||arr[x+1][y]==2||arr[x][y-1]==1||arr[x][y+1]==1){
return true;
}else if(arr[x-1][y]==2||arr[x+1][y]==1||arr[x][y-1]==1||arr[x][y+1]==1)
return true;
else
return false;
}else{
return false;
}
}
}