1547. Minimum cost of cutting stick

Title Description

There is a wooden stick with a length of N units, on which several positions are marked from 0 to n. For example, a stick with a length of 6 can be marked as follows:

Give you an integer array cuts, where cuts[i] indicates where you need to cut the stick.

You can finish the cutting in order or change the cutting order as needed.

The cost of each cutting is the length of the stick to be cut. The total cost of cutting the stick is the sum of the previous cutting costs. Cutting a stick will divide a stick into two smaller sticks (the sum of the lengths of the two sticks is the length of the stick before cutting). See the first example for a more intuitive explanation.

Returns the minimum total cost of cutting a stick.

Example 1:

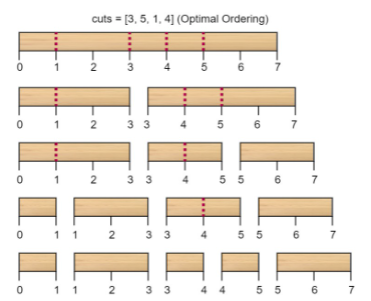
Input: n = 7, cuts = [1,3,4,5]
Output: 16
Explanation: cutting in the order of [1, 3, 4, 5] is as follows:

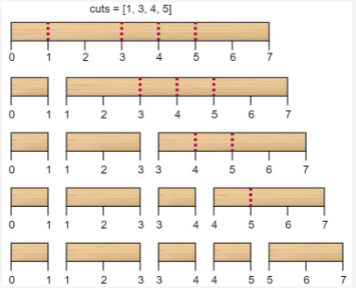
The first cut of a stick with a length of 7 costs 7. The second cut is a stick with a length of 6 (i.e. the second stick obtained from the first cut), the third cut is a stick with a length of 4, and the last cut is a stick with a length of 3. The total cost is 7 + 6 + 4 + 3 = 20.
When the cutting sequence is rearranged to [3, 5, 1, 4], the total cost = 16 (as shown in the example figure, 7 + 4 + 3 + 2 = 16).

Example 2:

Input: n = 9, cuts = [5,6,1,4,2]
Output: 22
Explanation: if cut in the given order, the total cost is 25. There are many cutting sequences with total cost < = 25. For example, the total cost of [4, 6, 5, 2, 1] is 22, which is the lowest among all possible schemes.

Tips:
2 <= n <= 10^6
1 <= cuts.length <= min(n - 1, 100)
1 <= cuts[i] <= n - 1
All integers in the cuts array are different from each other

Source: LeetCode
Link: https://leetcode-cn.com/problems/minimum-cost-to-cut-a-stick
The copyright belongs to Lingkou network. For commercial reprint, please contact the official authorization, and for non-commercial reprint, please indicate the source.

thinking

Interval dp, learning

class Solution {
    public int minCost(int n, int[] cuts) {
        //Interval dp
        //dp[i][j] represents the minimum total cost of cutting all the sticks when the left end point of the stick to be cut is cuts[i] and the right end point is cuts[j].
        //So how to update it,
        //First, add a cutting point at the left and right ends, 0 and n
        //There are cut [i + 1], cut [i + 2] in dp[i][j] Cut [J - 1] cutting points. Enumerate these cutting points to divide the stick into smaller parts
        //dp[i][j] = dp[i][k] + dp[k][j] + len;
        //That is, the sub problem

        int m = cuts.length;
        //Sort the cuts array, that is, sort the cutting points
        Arrays.sort(cuts);
        //Add the beginning and end points and copy them to the new array
        int[] cutss = new int[m + 2];

        cutss[0] = 0;
        cutss[m + 1] = n;

        System.arraycopy(cuts, 0, cutss, 1, m);

        int[][] dp = new int[m + 2][m + 2];
        //The cutting cost of two adjacent points is 0
        dp[0][0] = 0;
        for(int i = 1; i < m + 2; i++){
            dp[i][i] = 0;
            dp[i - 1][i] = 0;
        }
        
        //Because according to the update rule, i depends on what is larger than it and j depends on what is smaller than it, i traverses from large to large and j from small to large
        for(int i = m; i >= 0; i--){
            for(int j = i + 2; j < m + 2; j++){
                //If i and j are equal, there is only one cutting point,
                dp[i][j] = Integer.MAX_VALUE;
                //Traverse all split points
                for(int k = i + 1; k < j; k++){
                    dp[i][j] = Math.min(dp[i][j], dp[i][k] + dp[k][j]);
                }
                dp[i][j] += cutss[j] - cutss[i];
            }
        }
        return dp[0][m + 1];
    }
}

221. Maximum square

Title Description

In a two-dimensional matrix consisting of '0' and '1', find the largest square containing only '1' and return its area.

Example 1:

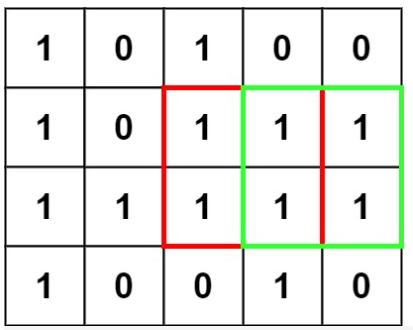
Input: matrix = [["1", "0", "1", "0", "0"], ["1", "0", "1", "1", "1"], ["1", "1", "1"], ["1", "0", "0", "1", "0"]]
Output: 4

Example 2:

Input: matrix = ["0", "1"], ["1", "0"]]
Output: 1

Example 3:

Input: matrix = [["0"]]
Output: 0

Tips:
m == matrix.length
n == matrix[i].length
1 <= m, n <= 300
matrix[i][j] is' 0 'or' 1 '

Source: LeetCode
Link: https://leetcode-cn.com/problems/maximal-square
The copyright belongs to Lingkou network. For commercial reprint, please contact the official authorization, and for non-commercial reprint, please indicate the source.

thinking

We can only think of using prefix and processing area, and then traverse the starting position and square side length, according to whether the prefix and processing area are equal to the square of side length
How to plan dynamically?

class Solution {
    public int maximalSquare(char[][] matrix) {
        //All I can think of is the prefix and sum of the matrix, and then traverse the starting position and the side length of the square to determine the largest square
        //It's just like the question of Niu Ke's simulated written test

        //How to dynamically plan
        //dp[i][j] represents the maximum square side length with (i,j) as the lower right corner
        //At this time, it is related to dp[i - 1][j], dp[i][j - 1], dp[i - 1][j - 1],
        //It's equal to the minimum of the three, plus 1
        //Because if you want to extend the side length of this square, the three values must be the same. Otherwise, the smallest one can only represent the current square
        
        int m = matrix.length;
        int n = matrix[0].length;

        int[][] dp = new int[m + 1][n + 1];
        int max = 0;
        for(int i = 1; i <= m; i++){
            for(int j = 1; j <= n; j++){
                if(matrix[i - 1][j - 1] == '0'){
                    dp[i][j] = 0;
                    continue;
                }
                dp[i][j] = Math.min(Math.min(dp[i - 1][j], dp[i][j - 1]), dp[i - 1][j - 1]) + 1;
                max = Math.max(max, dp[i][j]);
            }
        }
        return max * max;
    }
}

1312. The minimum number of inserts to make the string a palindrome string

Recommended questions this week

Title Description

Give you a string s, and you can insert any character anywhere in the string with each operation.

Please return the minimum number of operations to make s a palindrome string.

"Palindrome string" is a string with the same forward reading and reverse reading.

Example 1:

Input: s = "zzazz"
Output: 0
Explanation: the string "zzazz" is already a palindrome string, so no insertion operation is required.

Example 2:

Enter: s = "mbadm"
Output: 2
Explanation: the string can be changed to "mbdadbm" or "mdbabdm".

Example 3:

Enter: s = "leetcode"
Output: 5
Explanation: after inserting 5 characters, the string becomes "leetcodocteel".

Example 4:

Input: s = "g"
Output: 0

Example 5:

Enter: s = "no"
Output: 1

Tips:

1 <= s.length <= 500
All characters in s are lowercase letters.

Source: LeetCode
Link: https://leetcode-cn.com/problems/minimum-insertion-steps-to-make-a-string-palindrome
The copyright belongs to Lingkou network. For commercial reprint, please contact the official authorization, and for non-commercial reprint, please indicate the source.

thinking

At a glance, it is a moving gauge

class Solution {
    public int minInsertions(String s) {
        //dp[i][j] indicates the minimum number of operations in which I to j become a palindrome string
        //If s[i] and s[j] are the same, then dp[i + 1][j - 1]
        //If it is different, you need to add a character, either at the beginning or at the end, that is, consider dp[i + 1][j] (added at the end)
        //Or dp[i][j - 1] (added at the beginning)
        
        int l = s.length();
        int[][] dp = new int[l][l];

        //i depends on i+1 and j depends on j-1
        for(int i = l - 2; i >= 0; i--){
            for(int j = i + 1; j < l; j++){
                if(s.charAt(i) == s.charAt(j))
                    dp[i][j] = dp[i + 1][j - 1];
                else{
                    dp[i][j] = Math.min(dp[i][j - 1] + 1, dp[i + 1][j] + 1);
                }
            }
        }
        return dp[0][l - 1];
    }
}

Or you can think like this, that is, the practice of official dismissal 1:
The title indicates the minimum insertion operation to change a string into a palindrome string, which means that the length of the longest palindrome subsequence in the string needs to be added symmetrically to form a palindrome; So subtract the longest palindrome subsequence from the string length
This is not easy to understand