reminder
Hello, I'm Cbiltps. If there are difficult to understand sentences and key points that are difficult to express in words in my blog, I will have pictures. So my blog with pictures is very important!!!
If you want to know me better, please see my first blog, the link is as follows:
https://editor.csdn.net/md/?articleId=118778424
Key points of this chapter
- Detailed description of data types
- Storage of shaping in memory: original code, inverse code and complement code
- Introduction and judgment of byte order at large and small ends
- Storage and parsing of floating point in memory
Text start
1. Detailed introduction of data type
The basic built-in types we have learned so far:
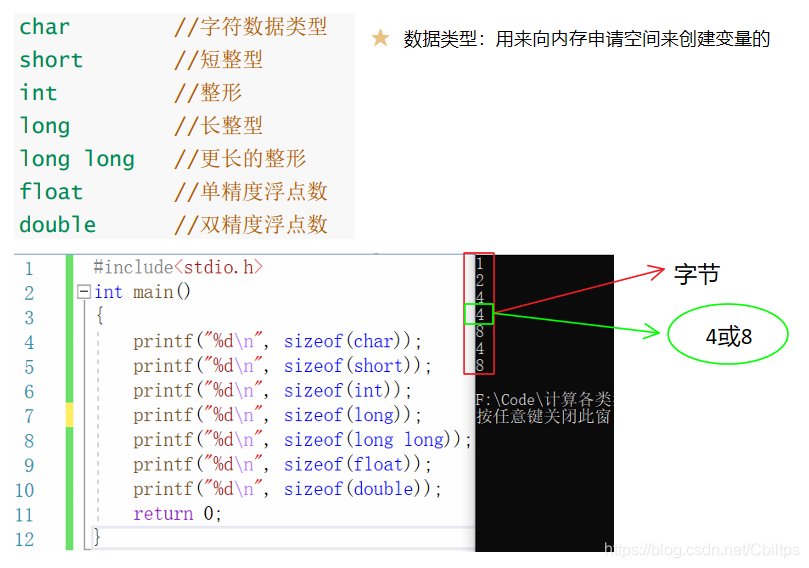
Why are there so many data types?
The type size determines the amount of memory used to create variables through this type, while the storage space size stores different ranges of data.
At this time, you can select the appropriate type according to the situation (improve memory utilization):
1. Too large selection: waste of space
2. Too small selection: insufficient space
1.1 basic classification of types
Plastic family:

be careful:
Whether char is signed or not depends on the compiler. Most compilers are signed
In this way, we can calculate some things:
Warm tip: the above knowledge involving the original code, inverse code and complement code will be explained below
Floating point family:

When to use float and when to use double?
1. There is no high requirement for accuracy. float is used and less space is used
2. When you need higher precision, use double to use more space
Construction type:

The above can be created by yourself
Take the array type as an example:
int arr[10] = {0};// What is the type of this array?
//The type of this array is int [10]
Pointer type:

Empty type:

The analysis is as follows:

2. Shaping the storage in memory
2.1 original code, inverse code and complement code
To know how data is stored in the opened memory? To know the following concepts!
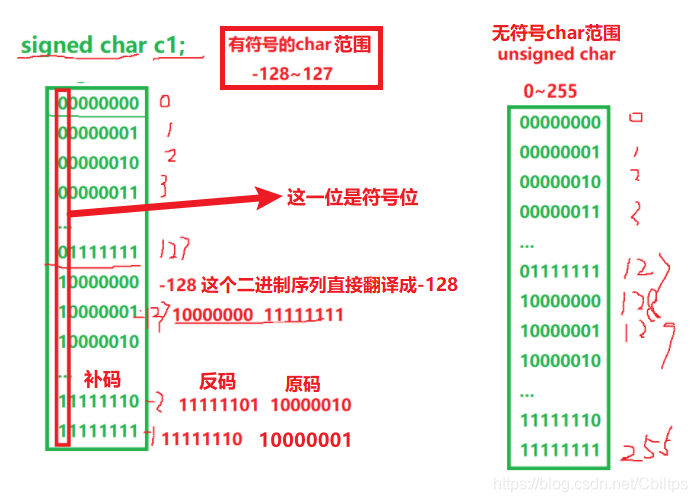
There are three representations of integers in computer, namely original code, inverse code and complement code.
The three representations have two parts: sign bit and numerical bit. Sign bit is 0 for "positive" and 1 for "negative", while the three representations of numerical bit negative integers are different. 
For shaping, the data stored in memory is actually a complement. Why
In computer systems, numerical values are always represented and stored by complements. The reason is that the symbol bit and value field can be processed uniformly by using complement;
At the same time, addition and subtraction can also be processed uniformly (CPU only has adder). In addition, complement and original code are converted to each other, and the operation process is the same, without additional hardware circuit.
The above words are difficult to understand. Please see the following diagram:

2.2 introduction to large and small terminals
First let's look at the problem?
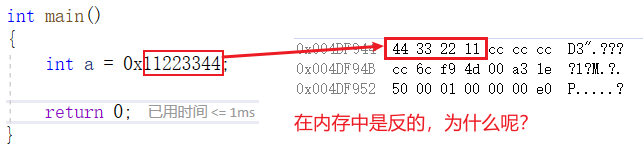
Because VS2019 uses small end byte order storage!
What is big end and small end


Why are there big and small ends?
In the computer system, we take bytes as the unit. Each address unit corresponds to a byte, and one byte is 8bit.
However, in C language, in addition to 8-bit char, there are 16bi short and 32bit long (depending on the specific compiler).
In addition, for processors with more than 8 bits, such as 16 bit or 32-bit processors, since the register width is greater than one byte, there must be a problem of how to arrange multiple bytes.
Therefore, there are large end storage mode and small end storage mode.
How to determine whether your device is in large byte order or small byte order**
This is Baidu's written test for system engineers in 2015!
Overcoming difficulties: open up an int, take the data of the lowest byte in the int and judge. However, if you want to take the lowest byte in int, you have to forcibly convert it to char *, because char * is a byte and just holds it.
Train of thought diagram: 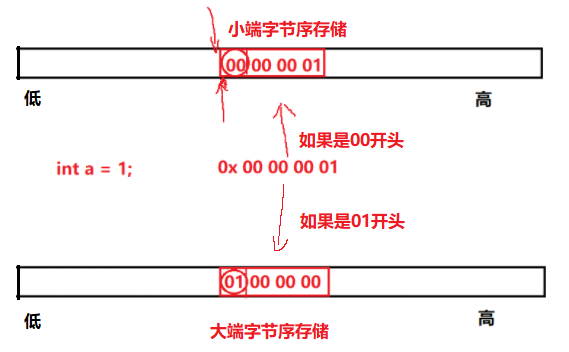
The code is as follows:
#include <stdio.h>
//int check_sys()
//{
// int a = 1;
// char* p = (char*)&a;
// if (*p == 1)
// return 1;
// else
// return 0;
//}
//After simplification
//
//int check_sys()
//{
// int a = 1;
// char* p = (char*)&a;
// /*if (*p == 1)
// return 1;
// else
// return 0;*/
// return *p;
//}
//After re simplification
int check_sys()
{
int a = 1;
return *(char*)&a;
}
int main()
{
int ret = check_sys();
if (1 == ret)
{
printf("Small end\n");
}
else
{
printf("Big end\n");
}
return 0;
}
2.3 practice
//Question 1;
int main()
{
char a = -1;
signed char b = -1;
unsigned char c = -1;
printf("a=%d,b=%d,c=%d", a, b, c);
return 0;
//Resolution:
// char a = -1;
// //1000000000000001 original code
// //11111111111111111111111111111111111110 inverse code
// //11111111111111111111111111111111111111111111 complement
// //11111111 -a char type is a byte. The following is the shaping and promotion
// //11111111111111111111111111111111
// //11111111111111111111111111111110
// //10000000000000000000000000000001 -1
//
// signed char b = -1;
// //11111111 -b
// unsigned char c = -1;
// //11111111 - C perform shaping and lifting below
// //00000000000000000000000011111111
// //00000000000000000000000011111111
// //00000000000000000000000011111111
// //%d - print as signed integers
// //
// printf("a=%d,b=%d,c=%d", a, b, c);
// //-1 -1 255
}
//Question 2:
int main()
{
char a = -128;
printf("%u\n",a);
return 0;
//Resolution:
// char a = -128;
// //10000000000000000000000010000000
// //11111111111111111111111101111111
// //11111111111111111111111110000000
// //10000000
// //11111111111111111111111110000000
//
// //%u print and shape in the form of unsigned numbers
//Question 3:
unsigned int i;
for(i = 9; i >= 0; i--)
{
printf("%u\n",i);
}
//Resolution:
//unsigned int i; Is unsigned
//So it's infinite
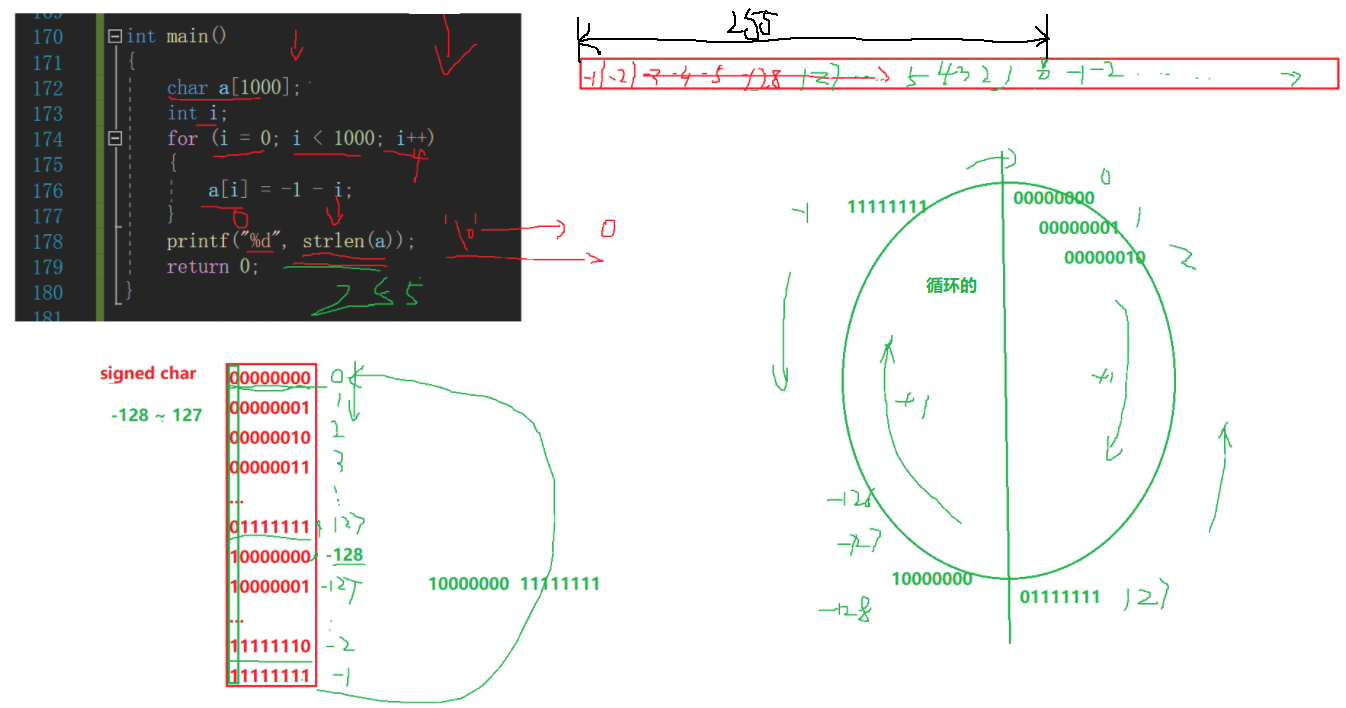
//Question 4
int main()
{
char a[1000];
int i;
for(i=0; i<1000; i++)
{
a[i] = -1-i;
}
printf("%d",strlen(a));//255
return 0;
}
Resolution:
3. Storage of floating point in memory
Common floating point numbers:
3.14159
1E10
The floating point family includes: float, double, long double types.
Range represented by floating point number: float Defined in H
3.1 an example
Examples of floating point storage:
int main()
{
int n = 9;
float *pFloat = (float *)&n;
printf("n The value of is:%d\n",n);
printf("*pFloat The value of is:%f\n",*pFloat);
*pFloat = 9.0;
printf("num The value of is:%d\n",n);
printf("*pFloat The value of is:%f\n",*pFloat);
return 0;
}
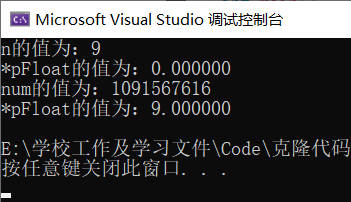
The output is like this. Why?
num and * pFloat are obviously the same number in memory. Why are the interpretation results of floating-point numbers and integers so different?
To understand this result, we must understand the representation of floating-point numbers in the computer.
3.2 floating point number storage rules
Detailed interpretation:
According to the international standard IEEE 754, any binary floating-point number V can be expressed in the following form:
- (-1)^S * M * 2^E
- (- 1)^s represents the sign bit. When s=0, V is a positive number; When s=1, V is negative.
- M represents a significant number, greater than or equal to 1 and less than 2.
- 2^E represents the exponential bit.
For example:
Decimal 5.0, written in binary, is 101.0, equivalent to 1.01 × 2^2 . Then, according to the above V format, we can get s=0, M=1.01, E=2.
Decimal * * - 5.0 * *, written in binary is - 101.0, equivalent to - 1.01 × 2^2 . Then, s=1, M=1.01, E=2.
However, some special examples are not considered, such as 3.3.
IEEE 754 states:
For 32-bit floating-point numbers, the highest 1 bit is the sign bit s, the next 8 bits are the exponent E, and the remaining 23 bits are the significant number M.

For 64 bit floating-point numbers, the highest bit is sign bit S, the next 11 bits are exponent E, and the remaining 52 bits are significant digits M.
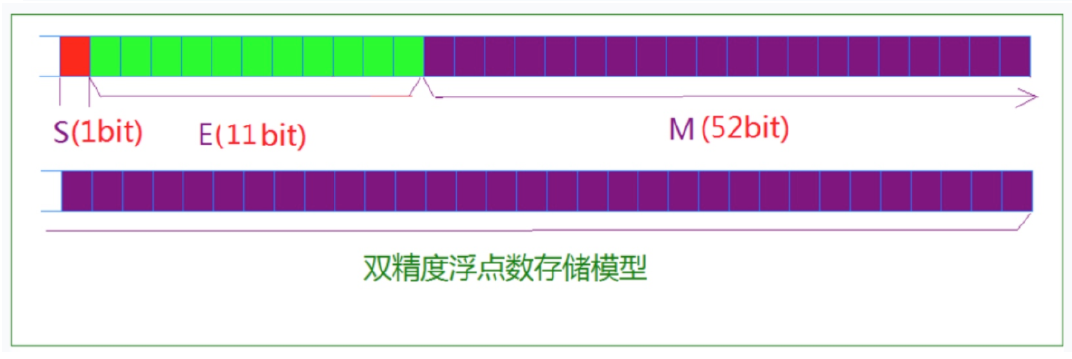
IEEE 754 has some special provisions on the significant number M and index E:
As mentioned earlier, 1 ≤ m < 2, that is, M can be written as 1 The form of xxxxxx, where xxxxxx represents the decimal part.
IEEE 754 stipulates that when saving M in the computer, the first digit of this number is always 1 by default, so it can be rounded off and only the following ones are saved.
xxxxxx part: for example, when saving 1.01, only 01 is saved. When reading, add the first 1.
The purpose of this is to save 1 significant digit. Take the 32-bit floating-point number as an example. There are only 23 bits left for M. after rounding off the 1 of the first bit, it is equivalent to saving 24 significant digits.
As for index E, the situation is more complicated.
First, E is an unsigned integer (unsigned int)
This means that if E is 8 bits, its value range is 0-255; If E is 11 bits, its value range is 0-2047.
However, we know that E in scientific counting can be negative, so IEEE 754 stipulates that the real value of e must be added with an intermediate number when stored in memory.
For 8-bit E, the median is 127; For an 11 bit E, the median is 1023.
For example, E of 2 ^ 10 is 10, so when saving as a 32-bit floating-point number, you must save 10 + 127 = 137, that is, 10001001.
Then, the index E can be extracted from the memory and can be divided into three cases:
E is not all 0 or all 1:
At this time, the floating-point number is represented by the following rule, that is, subtract 127 (or 1023) from the calculated value of index E to obtain the real value, and then add the first 1 before the significant number M.
For example, the binary form of 0.5 (1 / 2) is 0.1. Since it is specified that the positive part must be 1, that is, if the decimal point is shifted to the right by 1 digit, it will be 1.0 * 2 ^ (- 1), and its order code is - 1 + 127 = 126, which means 01111110, while the mantissa of 1.0 removes the integer part as 0 and complements 0 to 23 digits, then:
Its binary representation is: 0 01111110 00000000000000000000000
E is all 0:
At this time, the exponent E of the floating point number is equal to 1-127 (or 1-1023), which is the real value,
The significant number M is no longer added with the first 1, but is restored to 0 The decimal of XXXXXX.
This is done to represent ± 0 and small numbers close to 0.
E is all 1:
At this time, if the significant digits M are all 0, it means ± infinity. (positive and negative depending on sign bit s)
Illustration when E is all 0 or 1:
3.3 explain the previous example
int n = 9;
//0 00000000 00000000000000000001001
//E is all 0
//E is directly 1-127 = - 126
//M = 0.00000000000000000001001
//0.00000000000000000001001 * 2^-126
//This is a very small number, so the print out is 0.000000
float* pFloat = (float*)&n;
printf("n The value of is:%d\n", n);//9
printf("*pFloat The value of is:%f\n", *pFloat);//0.000000
*pFloat = 9.0;
//1001.0
//(-1)^0 * 1.001*2^3
//S=0
//E = 3
//3+127=129
//M = 1.001
//01000001000100000000000000000000
//So the binary print out is 1091567616
printf("num The value of is:%d\n", n);//1091567616
printf("*pFloat The value of is:%f\n", *pFloat);//9.000000
End of full text (conclusion)
If you see here, you have a comprehensive understanding of the storage of data in memory. If you are confused, you can comment or leave a private message.
If you like, just pay attention and praise.
Thank you again for reading and watching. Your support is my constant power!