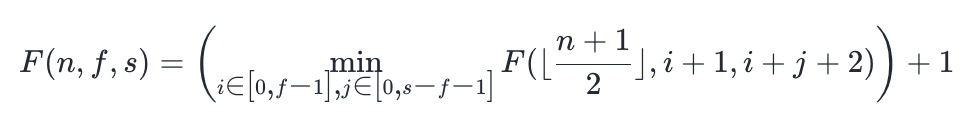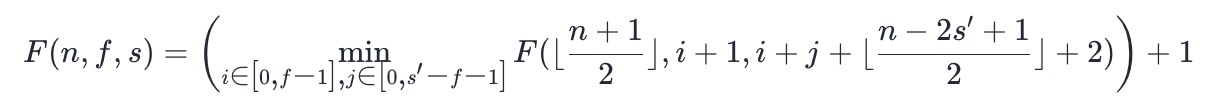1, Title Description

• N athletes participate in a championship. All athletes stand in a row and number from 1 to n according to the first position (athlete 1 is the first athlete in this row, athlete 2 is the second athlete, and so on).
• The championship consists of multiple rounds (starting from round 1). In each round, the ith athlete from the front to the back in this row needs to compete with the ith athlete from the back to the front. The winner will enter the next round. If the number of athletes in the current round is odd, the middle athlete will advance to the next round.
• For example, in the current round, athletes 1, 2, 4, 6 and 7 stand in a row:
• • Athlete 1 needs to compete with athlete 7;
• • Athlete 2 needs to compete with athlete 6;
• • The athlete advanced to the next round in four rounds.
• At the end of each round, the winners will be rearranged based on the original order (ascending order) assigned to them at the beginning.
• The athletes numbered first player and second player are the best athletes in this tournament. Before they start the competition, they can completely defeat any other athletes. When any two other athletes compete, either of them is likely to win. Therefore, who is the winner of this round can be determined.
• Give three integers n, firstPlayer and secondPlayer, and return an integer array composed of two values, representing the earliest rounds and the latest returns of the two best athletes in the tournament.
• Example 1:

Input: n = 11, firstPlayer = 2, secondPlayer = 4
 Output:[3,4]
Explanation:
One scenario that can generate the earliest number of rounds is:
Round 1:1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11
 Round 2:2, 3, 4, 5, 6, 11
 Round 3:2, 3, 4
 One scenario that can produce the latest number of returns is:
Round 1:1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11
 Round 2:1, 2, 3, 4, 5, 6
 Round 3:1, 2, 4
 Round 4:2, 4

• Example 2:

Input: n = 5, firstPlayer = 1, secondPlayer = 5
 Output:[1,1]
Explanation: the two best athletes 1 and 5 will compete in round 1.
There is no possibility for them to compete in other rounds

• Tips:
• • 2 <= n <= 28
• • 1 <= firstPlayer < secondPlayer <= n

2, Solution idea

① Dynamic programming, skillfully using symmetry to simplify the amount of calculation

• Obviously, the number of people in each round is halved until the first and second meet. Taking 28 people as an example, the number of people in each round is roundLens = [28, 14, 7, 4, 2].
• We remember that early [len] [firstPlayer] [secondPlayer] means that there are len people. When the indexes of the two strongest people are firstPlayer and secondPlayer respectively, the first round of meeting, and the last round means the latest round of meeting. Then, in this round of competition, firstPlayer and secondPlayer must win, and then we need to enumerate the victory and defeat of all other pairwise competitions, For each case, in the next round, firstPlayer and secondPlayer will appear in a new position, marked as nextFirst and nextSecond. Then earliest[len][firstPlayer][secondPlayer] is the minimum value of all earliest[len / 2][nextFirst][nextSecond], Similarly, latest[len][firstPlayer][secondPlayer] is the maximum value of all latest[len / 2][nextFirst][nextSecond].
• All early and late recursions from small to large still take 28 as an example, and the lengths to be calculated are [2, 4, 7, 14, 28] respectively. Different from ordinary dynamic programming, it is not necessary to calculate each len in a single use case, but only the len in roundLens; When len = 2, there is obviously only one case, that is, early [2] [0] [1] = latest [2] [0] [1] = 1, that is, there are only two people. The indexes of first player and second player must only be 0 and 1. They must meet in the first round, so they are 1 at the earliest and at the latest.
• Next, it is pushed in a large direction. In each round, all possible positions of firstPlayer and secondPlayer are enumerated, and all earliest and latest are calculated. Finally, earliest[n][firstPlayer - 1][secondPlayer - 1] is the answer. From the above ideas, we can see that the difficulty of this question is that after determining len, firstPlayer and secondPlayer in each round, what are the possible nextFirst and nextSecond in the next round?
• An obvious conclusion is that the answer has symmetry, which is reflected in two aspects. One is that the strongest two exchange positions, and the result is the same, that is, early [len] [firstplayer] [secondplayer] = early [len] [secondplayer] [firstplayer], which suggests that we only need to calculate the case of secondplayer > firstplayer; The second is that two people change to the mirror point at the same time, and the result is the same. For example, if there are 10 people and the indexes of the two strongest people are 0 and 1 respectively, then the mirror point of 0 is 9 and the mirror point of 1 is 8, so early [10] [0] [1] = early [10] [9] [8] = early [10] [8] [9].
• From the above conclusions, all the strongest points can be summarized into two cases, taking n = 10 as an example:
• • The first player is on the left, and the second player is on the left;
• • firstPlayer is on the left, secondPlayer is on the right, mirrorsecond > firstPlayer, for example, firstPlayer = 1, secondPlayer = 6, mirrorSecond = 3;
• • firstPlayer is on the left, secondPlayer is on the right, mirrorsecond < firstPlayer, for example, firstPlayer = 3, secondPlayer = 8, mirrorSecond = 1. In this case, it is equivalent to firstPlayer = 1 and secondPlayer = 6, which becomes scene b;
• • The first player is on the right side, and the second player is on the right side. It is changed into scene a by mirroring;
• First look at scenario a. first player will stay. Any one [0, first player] may be left in front of first player. Therefore, in the next round, the possible value of nextFirst is [0, first player]; secondPlayer must be left, and any number of intervals (firstPlayer, secondPlayer) may be left, and this number is not affected by firstPlayer and its previous number, so the possible values of nextSecond are [nextFirst + 1, nextFirst + secondPlayer - firstPlayer].
• Look at scenario b, the situation of nextFirst remains unchanged; secondPlayer will stay, half the interval [mirrorSecond, secondPlayer] will stay, and any interval (firstPlayer, mirrorSecond) may stay, so the possible value of nextSecond is [nextFirst + (secondPlayer - mirrorSecond) / 2, nextFirst + (secondPlayer - mirrorSecond) / 2 + mirrorSecond - firstPlayer].
• To sum up, enumerate all possible combinations of nextFirst and nextSecond. The minimum value of early [len / 2] [nextFirst] [nextSecond] is early [len] [firstplayer] [secondplayer].
• C + + example:

class Solution {
public:
    vector<int> earliestAndLatest(int n, int firstPlayer, int secondPlayer) {
        vector<int> roundLens;
        vector<vector<vector<int>>> earliest(n + 1, vector<vector<int>>(n, vector<int>(n, n + 1))), latest(n + 1, vector<vector<int>>(n, vector<int>(n, 0)));

        getRoundLens(n, roundLens);

        for (int roundLen : roundLens) {
            getEarliestAndLatest(roundLen, earliest, latest);
        }

        --firstPlayer, --secondPlayer;

        if (firstPlayer > secondPlayer) {
            swap(firstPlayer, secondPlayer);
        }

        if (firstPlayer >= n / 2 || n - secondPlayer <= firstPlayer) {  // Find the symmetrical position
            int tmpFirst = n - 1 - firstPlayer, tmpSecond = n - 1 - secondPlayer;
            firstPlayer = tmpSecond, secondPlayer = tmpFirst;
        }

        getEarliestAndLatest(n, firstPlayer, secondPlayer, earliest, latest);

        return { earliest[n][firstPlayer][secondPlayer], latest[n][firstPlayer][secondPlayer] };
    }

    void getRoundLens(int n, vector<int>& roundLens) {
        while (n > 2) {
            n = (n + 1) / 2;
            roundLens.push_back(n);
        }
        reverse(roundLens.begin(), roundLens.end());
    }

    void getEarliestAndLatest(int roundLen, vector<vector<vector<int>>>& earliest, vector<vector<vector<int>>>& latest) {
        for (int firstPlayer = 0; firstPlayer < roundLen - 1; ++firstPlayer) {
            for (int secondPlayer = firstPlayer + 1; secondPlayer < roundLen; ++secondPlayer) {
                getEarliestAndLatest(roundLen, firstPlayer, secondPlayer, earliest, latest);
            }
        }
    }

    void getEarliestAndLatest(int roundLen, int firstPlayer, int secondPlayer, vector<vector<vector<int>>>& earliest, vector<vector<vector<int>>>& latest) {
        if (firstPlayer + secondPlayer == roundLen - 1) {  // In a symmetrical position, the first round must meet
            earliest[roundLen][firstPlayer][secondPlayer] = latest[roundLen][firstPlayer][secondPlayer] = 1;
            return;
        }

        // Both numbers are on the right, or the second number is closer to the endpoint than the first number. Exchange the two numbers to a symmetrical position
        if (firstPlayer >= roundLen / 2 || roundLen - secondPlayer <= firstPlayer) {
            int tmpFirst = roundLen - 1 - firstPlayer, tmpSecond = roundLen - 1 - secondPlayer;
            earliest[roundLen][firstPlayer][secondPlayer] = earliest[roundLen][tmpSecond][tmpFirst];
            latest[roundLen][firstPlayer][secondPlayer] = latest[roundLen][tmpSecond][tmpFirst];
            return;
        }

        // In the next round, the first number can be anywhere in the interval [0, firstPlayer]
        int minNextFirst = 0, maxNextFirst = firstPlayer, minNextSecond = 0, maxNextSecond = 0, halfLen = (roundLen + 1) / 2;

        if (secondPlayer < (roundLen + 1) / 2) {  // If the second number is on the left, the second number in the next round can be anywhere after the first number [1, secondPlayer - firstPlayer]
            minNextSecond = 1, maxNextSecond = secondPlayer - firstPlayer;
        } else {  // If the second number is on the right, half of the interval [mirrorSecondPlayer, secondPlayer] must be left, and any number of intervals (first player, mirrorsecondplayer) can be left
            minNextSecond = secondPlayer - (roundLen / 2 - 1), maxNextSecond = minNextSecond + roundLen - 1 - secondPlayer - firstPlayer - 1;
        }

        for (int nextFirst = minNextFirst; nextFirst <= maxNextFirst; ++nextFirst) {
            for (int nextSecond = minNextSecond; nextSecond <= maxNextSecond; ++nextSecond) {
                earliest[roundLen][firstPlayer][secondPlayer] = min(earliest[roundLen][firstPlayer][secondPlayer], earliest[halfLen][nextFirst][nextFirst + nextSecond] + 1);
                latest[roundLen][firstPlayer][secondPlayer] = max(latest[roundLen][firstPlayer][secondPlayer], latest[halfLen][nextFirst][nextFirst + nextSecond] + 1);
            }
        }
    }
};

• Complexity analysis:
• • Time complexity: log n rounds need to be calculated. n2 is required for each round of enumeration of firstPlayer and secondPlayer, and n2 is required for enumeration of nextFirst and nextSecond. Therefore, the total time complexity is O (log n * N4).
• Space complexity: n3, although the array implementation is adopted, some space is not used.

② Randomized simulation

• Generate a combat effectiveness randomly for each athlete (ensure that the first player and second player are the largest and second largest). When two athletes compete, the one with higher combat effectiveness wins.
• Continuously simulate and count the maximum and minimum values of the rounds that firstPlayer and secondPlayer meet.
• If you look at the total time of all use cases, you need to set the simulation times according to the size of n.
• C + + example:

struct node {
    int a , b;
    bool operator <(const node &p) {
        return b < p.b;
    }
}player[30];

class Solution {
public:
    vector<int> earliestAndLatest(int n, int firstPlayer, int secondPlayer) {
        srand(time(NULL));

        // Set the number of simulations according to the size of n
        int N;
        if(n <= 10)
            N = 800;
        else if (n <= 20)
            N = 8000;
        else N = 38000;

        int ans1 = 9999 , ans2 = 0 , rest , now;
        
        while(N--)
        {
            // Remaining athletes
            rest = n;

            // Initialize combat effectiveness
            for(int i = 1 ; i <= n ; i++)
            {
                player[i].a = rand() % 1075943;
                player[i].b = i;
            }
            player[firstPlayer].a = 11000000;
            player[secondPlayer].a = 10999999;
            
            // Statistical rounds
            now = 1;
         
            // Simulation Competition
            while(rest > 1)
            {
                for(int i = 1 ; i <= rest / 2 ; i++)
                {
                    if(player[i].a < player[rest + 1 - i].a)
                        player[i] = player[rest + 1 - i];

                    // Count the maximum and minimum values of the encounter rounds of firstPlayer and secondPlayer
                    if(player[i].b == firstPlayer && player[rest + 1 - i].b == secondPlayer)
                        ans1 = min(ans1 , now) , ans2 = max(ans2 , now);
                }
                now++;
                rest = (rest + 1) / 2;
                sort(player + 1 , player + rest + 1);
            }
        }
        
        vector<int> ans = {ans1 , ans2};
        return ans;

    }
};

③ Analysis of essentially different stations + memorized search (Leetcode official solution)

• We can use F(n,f,s) to represent the earliest rounds when there are still n people left, and the two best athletes are the F and s athletes from left to right in a row. Similarly, we use G(n,f,s) to represent the latest involution number of their competition, so how to carry out state transition?
• If we simply use F(n,f,s) for state transition, the designed algorithm and the written code will be quite complex. For example, we need to consider so many cases, so the state transition equation is quite troublesome.
• We can consider analyzing the situation of essentially different stations, as shown below:

• Its correctness lies in:
• • F(n,f,s)=F(n,s,f) is constant, that is, exchange the positions of the two best athletes, and the results will not change;
• • F(n,f,s)=F(n,n+1 − s,n+1 − f) is always true, because we will let the ith athlete from the front to the back compete with the ith athlete from the back to the front. Then all athletes will be regarded as a whole and the whole will be turned over, and the result will not change.
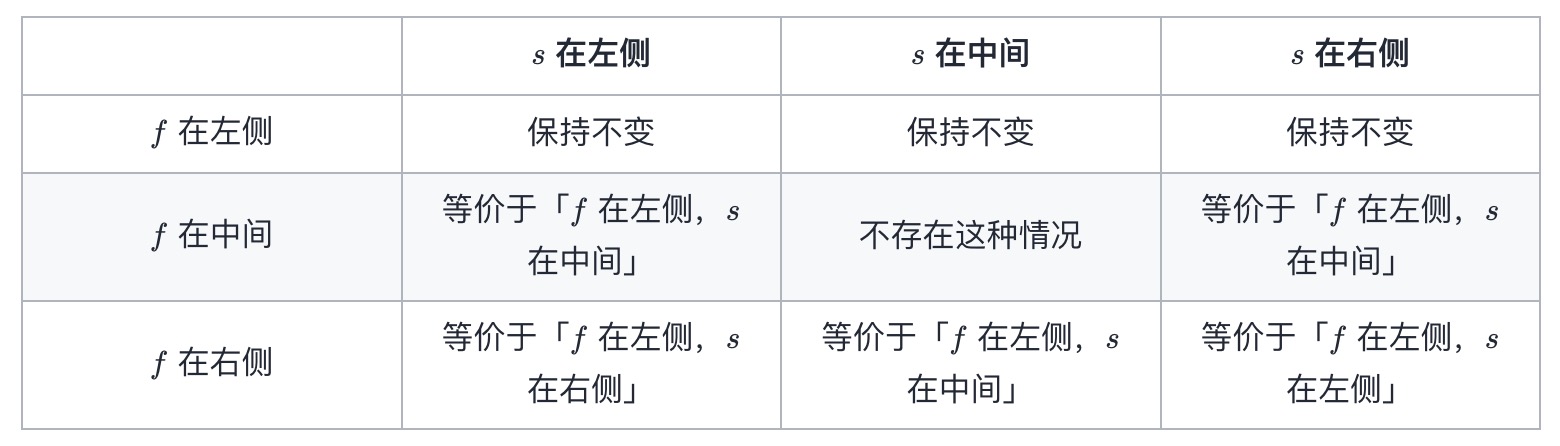
• Using these two transformation rules, we can ensure that in F(n,f,s), f must be less than s, then f must be on the left, and s can be on the left, middle or right. In this way, we reduce the original 8 cases to 3 cases. For G(n,f,s), the method is exactly the same.
• Now that we know that f must be on the left, we can design the state transition equation according to whether s is on the left, in the middle or on the right: if s is on the left, as shown in the figure below:
• • F there are f − 1 athletes on the left, and they will compete with the corresponding athletes on the right, so there are [0,f − 1] athletes left;
• • There is s − f − 1 athlete between F and S. they will compete with the corresponding athlete on the right, so there are [0,s − f − 1] athletes left.

• If there are i athletes left in F − 1 and j athletes left in s − f − 1, then in the next round, the two best athletes are in position i+1 and position i+j+2 respectively, and the total number of remaining athletes is [(n+1)/2], where ⌊ x ⌋ represents rounding down x, so the state transition equation can be obtained:

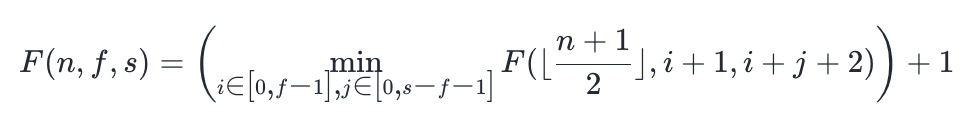
• If s is in the middle, as shown in the figure below, it can be found that the state transition equation is exactly the same as that of s on the left:

• If s is on the right, the situation will be more troublesome. There are three situations:
• • The simplest case is that f and s just compete, that is, f+s=n+1, then F(n,f,s)=1;
• • In addition, let s' = n+1 − s compete with s in this round, then f < s' is one case and F > s' is another case.
• However, we can know that according to the analysis of "essentially different station conditions" above, f is changed into n+1 − s and S is changed into n+1 − F, so f is still less than s and F is also less than s', so only the case of F < s' needs to be considered, as shown in the following figure:
• • F there are f − 1 athletes on the left, and they will compete with the corresponding athletes on the right, so there are [0,f − 1] athletes left;
• • There is s ′− f − 1 athlete between F and s', they will compete with the corresponding athlete on the right, so there are [0,s ′− f − 1] athletes left;
• • S' must lose to s;
• • There are n − 2s' Athletes between s' and S. if n − 2s' is an even number, they compete with each other, leaving (n − 2s') / 2 athletes; If n − 2s' is an odd number, one of them will be empty, and the remaining two will compete with each other, leaving (n − 2s' + 1) / 2 athletes. Therefore, whether n − 2s' is odd or even, there must be ⌊ (n − 2s' + 1) / 2 athletes between s' and s.

• If there are i athletes left in F − 1 and j athletes left in s ′− f − 1, then in the next round, the two best athletes are located in position i+1 and position i+j + ⌊ (n − 2s ′ + 1) / 2 ⌋ + 2 respectively, so the state transition equation can be obtained:

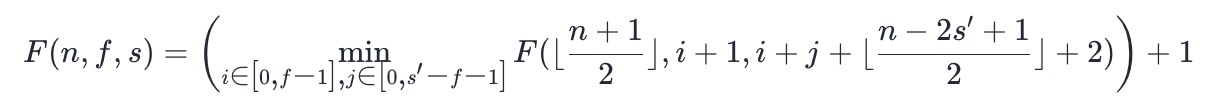
• In this way, we get all the state transition equations about F, and for the state transition equation about G, we only need to change all min to max.
• According to the above two transformation rules, which rules should be used when n, F and s meet the relationship (rather than the abstract "left", "middle", "right")? There are many design methods, such as a relatively simple method used in the problem solving Code:
• • Firstly, we use top-down memory search instead of dynamic programming for state transition, which is more concise and intuitive, and there is no need to consider the evaluation order of states;
• • The entry of the memory search is F(n,firstPlayer,secondPlayer). Before starting the memory search, first make the firstPlayer smaller than the secondPlayer through the transformation rule F(n,f,s)=F(n,s,f). In this way, because another transformation rule F(n,f,s)=F(n,n+1 − s,n+1 − f) will not change the size relationship between F and s, in the next memory search, F < s is constant, so we don't need to use the transformation rule F(n,f,s)=F(n,s,f);
• • In the above table, there are five situations that we need to change, namely, "F in the middle, s on the left", "F in the middle, s on the right", "F on the right, s on the left", "F on the right, s in the middle", "F on the right, s on the right". Since f < s is constant, only two of these five situations need to be handled, That is, "F in the middle, s on the right" and "F on the right, s on the right". In addition, in the section "design of state transition equation", we also found a case to be handled, that is, "F is on the left, s is on the right, and F > s' = n+1 − s". Can these three situations be unified? For the last case, we have F + s > n+1, and "F is in the middle, s is on the right" and "F is on the right, s is on the right" also just satisfy f + s > n+1, and all cases that do not need transformation do not satisfy f + s > n+1. Therefore, we only need to use the transformation rule F(n,f,s)=F(n,n+1 − s,n+1 − f) once when F + s > n+1.
• Since @ cache can be easily used for memory search in Python, there is no need to explicitly define F and G in the following Python code. The binary returned by function dp(n,f,s) is F(n,f,s) and G(n,f,s). Examples are as follows:

class Solution:
    def earliestAndLatest(self, n: int, firstPlayer: int, secondPlayer: int) -> List[int]:
        @cache
        def dp(n: int, f: int, s: int) -> (int, int):
            if f + s == n + 1:
                return (1, 1)
            
            # F(n,f,s)=F(n,n+1-s,n+1-f)
            if f + s > n + 1:
                return dp(n, n + 1 - s, n + 1 - f)
            
            earliest, latest = float("inf"), float("-inf")
            n_half = (n + 1) // 2

            if s <= n_half:
                # s is on the left or in the middle
                for i in range(f):
                    for j in range(s - f):
                        x, y = dp(n_half, i + 1, i + j + 2)
                        earliest = min(earliest, x)
                        latest = max(latest, y)
            else:
                # s on the right
                # s'
                s_prime = n + 1 - s
                mid = (n - 2 * s_prime + 1) // 2
                for i in range(f):
                    for j in range(s_prime - f):
                        x, y = dp(n_half, i + 1, i + j + mid + 2)
                        earliest = min(earliest, x)
                        latest = max(latest, y)
            
            return (earliest + 1, latest + 1)

        # F(n,f,s) = F(n,s,f)
        if firstPlayer > secondPlayer:
            firstPlayer, secondPlayer = secondPlayer, firstPlayer
        
        earliest, latest = dp(n, firstPlayer, secondPlayer)
        dp.cache_clear()
        return [earliest, latest]

• C + + example:

class Solution {
private:
    int F[30][30][30], G[30][30][30];

public:
    pair<int, int> dp(int n, int f, int s) {
        if (F[n][f][s]) {
            return {F[n][f][s], G[n][f][s]};
        }
        if (f + s == n + 1) {
            return {1, 1};
        }

        // F(n,f,s)=F(n,n+1-s,n+1-f)
        if (f + s > n + 1) {
            tie(F[n][f][s], G[n][f][s]) = dp(n, n + 1 - s, n + 1 - f);
            return {F[n][f][s], G[n][f][s]};
        }

        int earlist = INT_MAX, latest = INT_MIN;
        int n_half = (n + 1) / 2;

        if (s <= n_half) {
            // On the left or in the middle
            for (int i = 0; i < f; ++i) {
                for (int j = 0; j < s - f; ++j) {
                    auto [x, y] = dp(n_half, i + 1, i + j + 2);
                    earlist = min(earlist, x);
                    latest = max(latest, y);
                }
            }
        }
        else {
            // s on the right
            // s'
            int s_prime = n + 1 - s;
            int mid = (n - 2 * s_prime + 1) / 2;
            for (int i = 0; i < f; ++i) {
                for (int j = 0; j < s_prime - f; ++j) {
                    auto [x, y] = dp(n_half, i + 1, i + j + mid + 2);
                    earlist = min(earlist, x);
                    latest = max(latest, y);
                }
            }
        }

        return {F[n][f][s] = earlist + 1, G[n][f][s] = latest + 1};
    }

    vector<int> earliestAndLatest(int n, int firstPlayer, int secondPlayer) {
        memset(F, 0, sizeof(F));
        memset(G, 0, sizeof(G));

        // F(n,f,s) = F(n,s,f)
        if (firstPlayer > secondPlayer) {
            swap(firstPlayer, secondPlayer);
        }

        auto [earlist, latest] = dp(n, firstPlayer, secondPlayer);
        return {earlist, latest};
    }
};

• Complexity analysis:
• • Time complexity: O(n4logn). In state F(n,f,s) (G(n,f,s), the range of each dimension is O(n), and each state requires O(n2) time to enumerate all states that can be transferred. Therefore, the time complexity of the whole algorithm is O(n5). However, it can be found that the number of values of N in F(n,f,s) is limited. In the process of memory search, n will become ⌊ (n+1)/2 ⌋ and continue to recurse downward. Therefore, the number of values of n is only O(logn), that is, the total time complexity is O(n4logn).
• • Space complexity: O(n2logn) or O(n3), which is the space required to store all States. In C + + code, an array is used to store all States. Even if the number of values of n is only O(logn), it is still necessary to open up O(n) space for the first dimension. In Python code, @ cache uses the tuple tuple as the key of dictionary dict to store the values of all States. If the number of States is O(n2logn), the space used is O(n2logn).