Original link: http://tecdat.cn/?p=12227
Original source: Tuo end data tribal official account
abstract
This paper describes the analysis process of Markov transformation model in R language. Firstly, the simulation data set is modeled in detail. Next, the Markov transformation model is fitted to a real data set with discrete response variables. Different methods used to validate modeling of these data sets.
Simulation example
The sample data is a simulated data set that shows how to detect the existence of two different modes: the response variables in one mode are highly correlated, and the response in the other mode depends only on the exogenous variable x. The autocorrelation observations range from 1 to 100, 151 to 180, and 251 to 300. The real model of each scheme is: 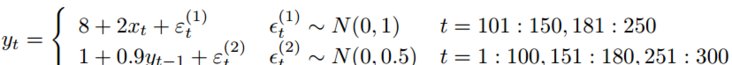
The curve in Figure 1 shows that in the interval where there is no autocorrelation, the response variable y has a similar behavior to the covariate X. Fit the linear model to study how covariate x explains variable response y.
> summary(mod) Call: lm(formula = y ~ x, data = example) Residuals: Min 1Q Median 3Q Max -2.8998 -0.8429 -0.0427 0.7420 4.0337 > plot(ts(example))
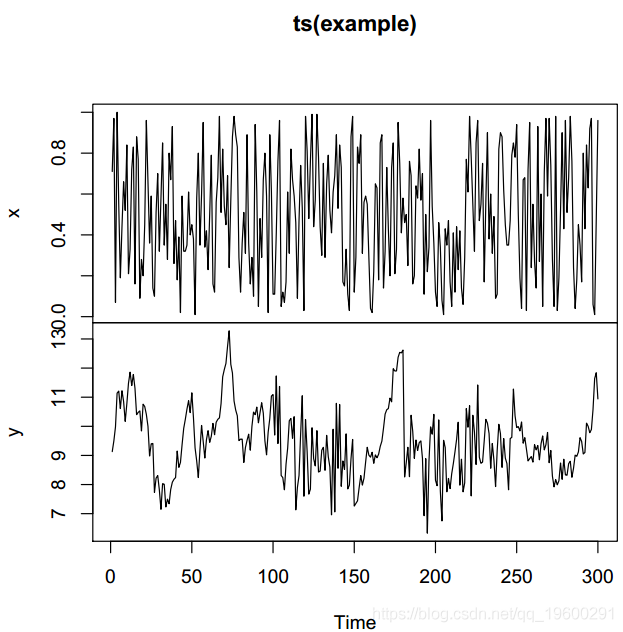
Figure 1: simulated data, y variable is the response variable
Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 9.0486 0.1398 64.709 < 2e-16 *** x 0.8235 0.2423 3.398 0.00077 *** Residual standard error: 1.208 on 298 degrees of freedom Multiple R-squared: 0.03731, Adjusted R-squared: 0.03408 F-statistic: 11.55 on 1 and 298 DF, p-value: 0.0007701
Covariates are really important, but the data behavior explained by the model is very bad. The linear model residual diagram in Figure 1 shows that they have strong autocorrelation. The diagnostic diagram of the residuals (Fig. 2) confirms that they do not appear to be white noise and have autocorrelation. Next, the autoregressive Markov transformation model (MSM-AR) is fitted to the data. The autoregressive part is set to 1. In order to indicate that all parameters can be different in two cycles, the transformation parameters are (sw) is set as a vector with four components. The last value when fitting the linear model is called the residual.

Standard deviation. There are options to control the estimation process, such as logical parameters that indicate whether process parallelization has been completed.
Markov Switching Model AIC BIC logLik 637.0736 693.479 -312.5368 Coefficients: Regime 1 \-\-\-\-\-\-\-\-\- Estimate Std. Error t value Pr(>|t|) (Intercept)(S) 0.8417 0.3025 2.7825 0.005394 ** x(S) -0.0533 0.1340 -0.3978 0.690778 y_1(S) 0.9208 0.0306 30.0915 < 2.2e-16 *** \-\-\- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 0.5034675 Multiple R-squared: 0.8375 Standardized Residuals: Min Q1 Med Q3 Max -1.5153666657 -0.0906543311 0.0001873641 0.1656717256 1.2020898986 Regime 2 --------- Estimate Std. Error t value Pr(>|t|) (Intercept)(S) 8.6393 0.7244 11.9261 < 2.2e-16 *** x(S) 1.8771 0.3107 6.0415 1.527e-09 *** y_1(S) -0.0569 0.0797 -0.7139 0.4753 \-\-\- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 0.9339683 Multiple R-squared: 0.2408 Standardized Residuals: Min Q1 Med Q3 Max -2.31102193 -0.03317756 0.01034139 0.04509105 2.85245598 Transition probabilities: Regime 1 Regime 2 Regime 1 0.98499728 0.02290884 Regime 2 0.01500272 0.97709116
Model mod MSWM has a very significant state of covariance x, and in other cases, autocorrelation variables are also very important. Both have high values of R square. Finally, the transition probability matrix has a high value, which indicates that it is difficult to change from on state to another state. The model can perfectly detect the period of each state. The residuals look like white noise, and they are suitable for normal distribution. Moreover, the autocorrelation disappeared.


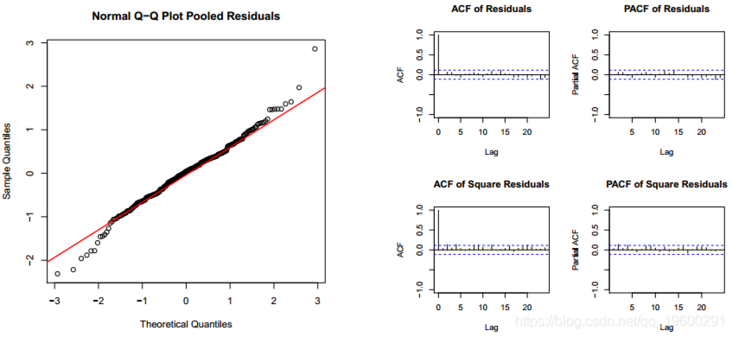

The graphical display has perfectly detected the cycle of each scheme.
> plot(mod.mswm,expl="x")

traffic accident
The traffic data include the daily number of traffic accidents, average daily temperature and daily precipitation in Spain in 2010. The purpose of the data is to study the relationship between the number of deaths and climatic conditions. Since there are different behaviors between weekend and weekday variables, we illustrate the use of generalized Markov transformation model in this case.
In this example, the response variable is the count variable. Therefore, we fit the Poisson generalized linear model.
> summary(model) Call: glm(formula = NDead ~ Temp + Prec, family = "poisson", data = traffic)

Deviance Residuals: Min 1Q Median 3Q Max -3.1571 -1.0676 -0.2119 0.8080 3.0629 Coefficients: Estimate Std. Error z value Pr(>|z|) (Intercept) 1.1638122 0.0808726 14.391 < 2e-16 *** Temp 0.0225513 0.0041964 5.374 7.7e-08 *** Prec 0.0002187 0.0001113 1.964 0.0495 * \-\-\- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 (Dispersion parameter for poisson family taken to be 1) Null deviance: 597.03 on 364 degrees of freedom Residual deviance: 567.94 on 362 degrees of freedom AIC: 1755.9 Number of Fisher Scoring iterations: 5
Next, a fitting Markov transformation model is used. In order to adapt to the generalized Markov transformation model, family parameters must be included, and glm has no standard deviation parameters, so sw parameters do not include its switching parameters.
> Markov Switching Model AIC BIC logLik 1713.878 1772.676 -850.9388 Coefficients: Regime 1 \-\-\-\-\-\-\-\-\- Estimate Std. Error t value Pr(>|t|) (Intercept)(S) 0.7649 0.1755 4.3584 1.31e-05 *** Temp(S) 0.0288 0.0082 3.5122 0.0004444 *** Prec(S) 0.0002 0.0002 1.0000 0.3173105 \-\-\- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Regime 2 \-\-\-\-\-\-\-\-\- Estimate Std. Error t value Pr(>|t|) (Intercept)(S) 1.5659 0.1576 9.9359 < 2e-16 *** Temp(S) 0.0194 0.0080 2.4250 0.01531 * Prec(S) 0.0004 0.0002 2.0000 0.04550 * \-\-\- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Transition probabilities: Regime 1 Regime 2 Regime 1 0.7287732 0.4913893 Regime 2 0.2712268 0.5086107
Both states have significant covariates, but precipitation covariates are significant only in one of the two states.
Aproximate intervals for the coefficients. Level= 0.95 (Intercept): Lower Estimation Upper Regime 1 0.4208398 0.7648733 1.108907 Regime 2 1.2569375 1.5658582 1.874779 Temp: Lower Estimation Upper Regime 1 0.012728077 0.02884933 0.04497059 Regime 2 0.003708441 0.01939770 0.03508696 Prec: Lower Estimation Upper Regime 1 -1.832783e-04 0.0001846684 0.0005526152 Regime 2 -4.808567e-05 0.0004106061 0.0008692979

Since the model is an extension of the general linear model, the Pearson residual in the graph is calculated from the class object. The residual has the classical structure of white noise. The residuals are not autocorrelated, but they do not agree with the normal distribution. However, the normality of Pearson residuals is not the key condition for the verification of generalized linear models.
> plot(m1,which=2)
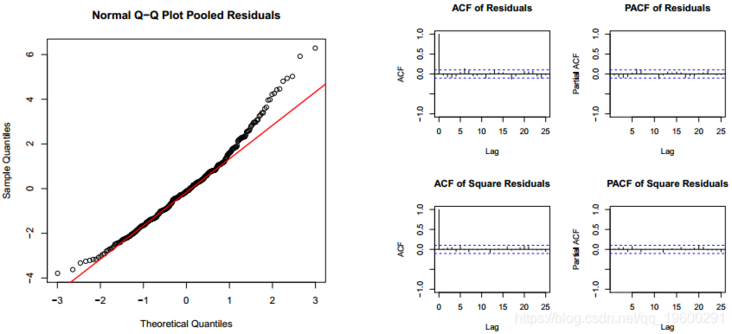

We can see the status allocation in a short time, because the larger status basically includes working days.

Most popular insights
1.Simulation of hybrid queuing stochastic service queuing system with R language
2.Using queuing theory to predict waiting time in R language
3.Implementation of Markov chain Monte Carlo MCMC model in R language
4.Markov Regime Switching Model in R language Model ")
5.matlab Bayesian hidden Markov hmm model
6.Simulation of hybrid queuing stochastic service queuing system with R language
7.Python portfolio optimization based on particle swarm optimization
8.Research on traffic casualty accident prediction based on R language Markov transformation model