Sorting algorithm

Reference website:

1. Ten classical sorting algorithms
2. Ten classic sorting algorithms · Python code display

Algorithm classification

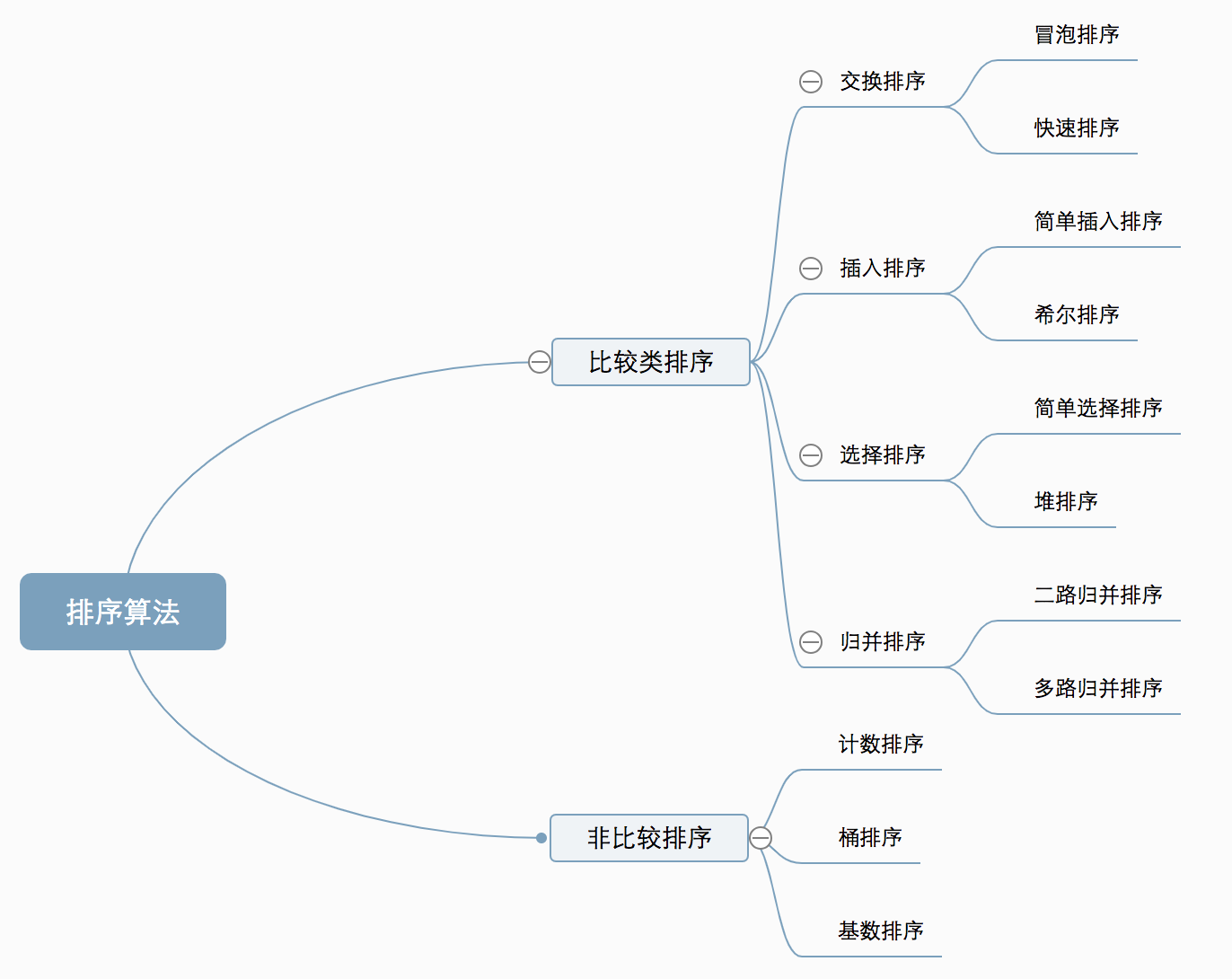
Related concepts

Comparison sort: the relative order between elements is determined by comparison. Because its time complexity cannot exceed O(nlogn), it is also called nonlinear time comparison sort.
Non comparison sort: it does not determine the relative order between elements through comparison. It can break through the time lower bound based on comparison sort and run in linear time. Therefore, it is also called linear time non comparison sort.

Algorithm complexity

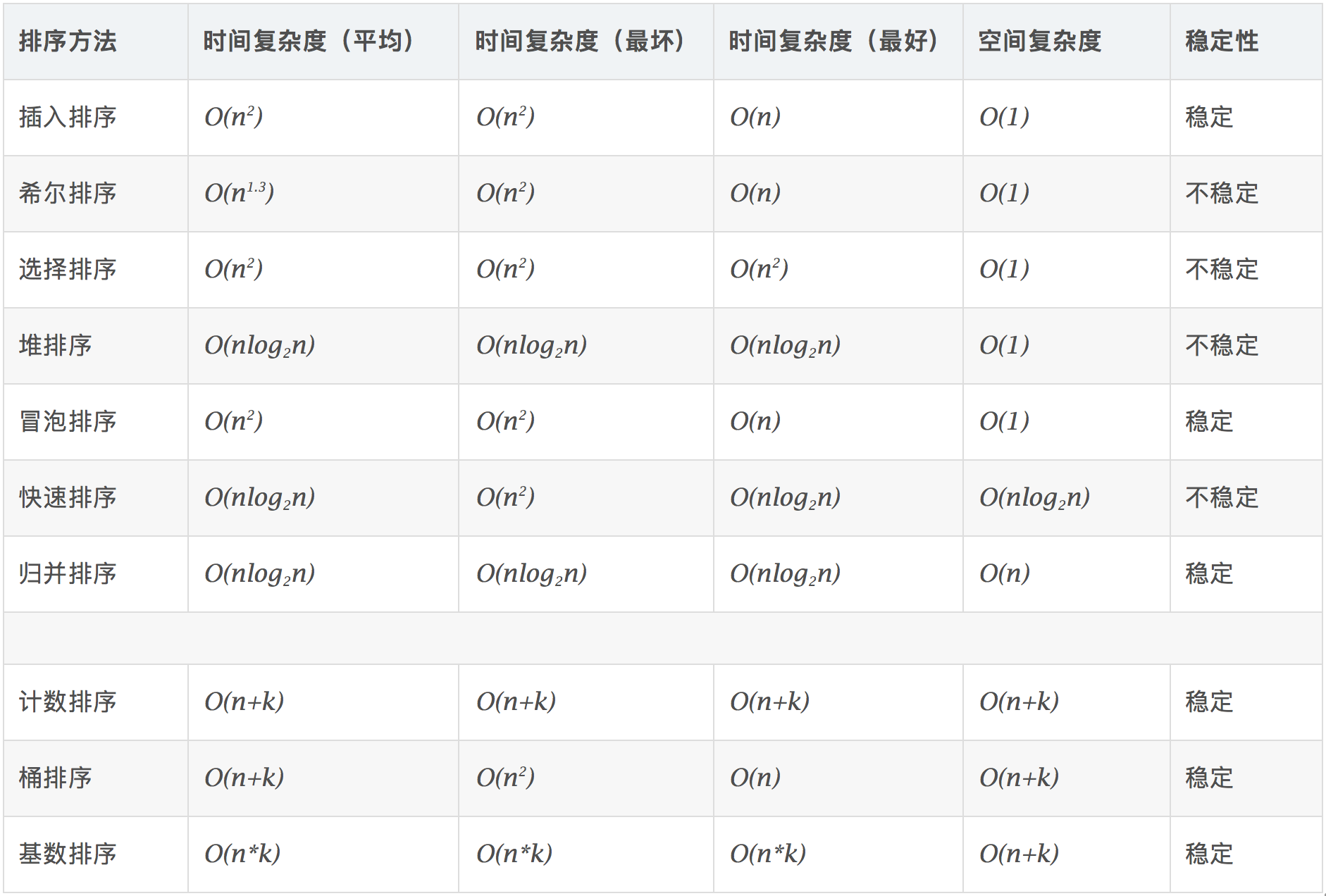
Related concepts

Stable: if a was in front of b and a=b, a will still be in front of b after sorting.
Unstable: if a was originally in front of b and a=b, a may appear after b after sorting.
Time complexity: the total number of operations on sorting data. Reflect the law of operation times when n changes.
Spatial complexity: refers to the measurement of the storage space required for the implementation of the algorithm in the computer. It is also a function of the data scale n.

Text introduction

Note: This article only provides concepts and results. If you need to understand the execution process, you can obtain the execution process through editor breakpoint debugging.

• Bubble Sort

1. Compare adjacent elements. If the first one is bigger than the second, exchange them.
2. Do the same for each pair of adjacent elements, from the first pair at the beginning to the last pair at the end, so that the last element should be the largest number.
3. Repeat the above steps for all elements except the last one.
4. Repeat steps 1 to 3 until the sorting is completed.

• Selection Sort

1. Initial state: the disordered region is R[1... n], and the ordered region is empty.
2. At the beginning of the i-th sequence (i=1,2,3... n-1), the current ordered area and unordered area are R[1... i-1] and R(i... n) respectively. This sequence selects the record R[k] with the smallest keyword from the current unordered area and exchanges it with the first record R in the unordered area, so that R[1... I] and R[i+1... n) become a new ordered area with an increase in the number of records and a new unordered area with a decrease in the number of records.
3. At the end of n-1 trip, the array is ordered.

• Insertion Sort

1. Starting with the first element, the element can be considered to have been sorted.
2. Take out the next element and scan forward from the back in the sorted element sequence.
3. If the element (sorted) is larger than the new element, move the element to the next position.
4. Repeat step 3 until you find a location where the sorted element is less than or equal to the new element.
5. After the new element is inserted into this location.
6. Repeat steps 2 to 5.

• Shell Sort

1. Select an incremental sequence t1, t2,..., tk, where ti > TJ, tk=1.
2. Sort the sequence k times according to the number of incremental sequences k.
3. For each sorting, the sequence to be sorted is divided into several subsequences with length m according to the corresponding increment ti, and each sub table is directly inserted and sorted. Only when the increment factor is 1, the whole sequence is treated as a table, and the table length is the length of the whole sequence.

• Merge Sort

1. The input sequence with length n is divided into two subsequences with length n/2.
2. The two subsequences are sorted by merging.
3. Merge two sorted subsequences into a final sorting sequence.

• Quick Sort

1. Picking out an element from a sequence is called a "pivot".
2. Reorder the sequence. All elements smaller than the benchmark value are placed in front of the benchmark, and all elements larger than the benchmark value are placed behind the benchmark (the same number can be on either side). After the partition exits, the benchmark is in the middle of the sequence. This is called partition operation.
3. Recursively sorts subsequences that are smaller than the reference value element and subsequences that are larger than the reference value element.

• Heap Sort

1. Build the initial keyword sequence to be sorted (R1,R2,... Rn) into a large top heap, which is the initial unordered area.
2. Exchange the top element R[1] with the last element R[n]. At this time, a new disordered region (R1,R2,... Rn-1) and a new ordered region (Rn) are obtained, and R[1,2... N-1] < = R[n].
3. Since the new heap top R[1] may violate the nature of the heap after exchange, it is necessary to adjust the current unordered area (R1,R2,... Rn-1) to a new heap, and then exchange R[1] with the last element of the unordered area again to obtain a new unordered area (R1,R2,... Rn-2) and a new ordered area (Rn-1,Rn). Repeat this process until the number of elements in the ordered area is n-1, and the whole sorting process is completed.

• Counting Sort

1. Find the largest and smallest elements in the array to be sorted.
2. Count the number of occurrences of each element with value i in the array and store it in item i of array C.
3. All counts are accumulated (starting from the first element in C, and each item is added to the previous item).
4. Reverse fill the target array: put each element i in item C(i) of the new array, and subtract 1 from C(i) for each element.

• Bucket Sort [data length must be exactly the same]

1. Set a quantitative array as an empty bucket.
2. Traverse the input data and put the data into the corresponding bucket one by one.
3. Sort each bucket that is not empty.
4. Splice the ordered data from a bucket that is not empty.

• Radix Sort

1. Gets the maximum number in the array and the number of bits.
2. arr is the original array, and each bit is taken from the lowest bit to form a radius array.
3. Count and sort the radix (using the characteristics that count sorting is suitable for a small range of numbers).

JavaScript coding case

1. Bubble Sort

function bubbleSort(arr) {
    var len = arr.length;
    for(var i = 0; i < len - 1; i++) {
        for(var j = 0; j < len - 1 - i; j++) {
            if(arr[j] > arr[j+1]) {       // Pairwise comparison of adjacent elements
                var temp = arr[j+1];       // Element exchange
                arr[j+1] = arr[j];
                arr[j] = temp;
            }
        }
    }
    return arr;
}

2. Selection Sort

function selectionSort(arr) {
    var len = arr.length;
    var minIndex, temp;
    for(var i = 0; i < len - 1; i++) {
        minIndex = i;
        for(var j = i + 1; j < len; j++) {
            if(arr[j] < arr[minIndex]) {    // Find the smallest number
                minIndex = j;                // Save the index of the smallest number
            }
        }
        temp = arr[i];
        arr[i] = arr[minIndex];
        arr[minIndex] = temp;
    }
    return arr;
} 

3. Insertion Sort

function insertionSort(arr) {
    var len = arr.length;
    var preIndex, current;
    for(var i = 1; i < len; i++) {
        preIndex = i - 1;
        current = arr[i];
        while(preIndex >= 0 && arr[preIndex] > current) {
            arr[preIndex + 1] = arr[preIndex];
            preIndex--;
        }
        arr[preIndex + 1] = current;
    }
    return arr;
}

4. Shell Sort

function shellSort(arr) {
    var len = arr.length;
    for(var gap = Math.floor(len / 2); gap > 0; gap = Math.floor(gap / 2)) {
        // Note: This is different from the dynamic diagram. The dynamic diagram is executed in groups, and the actual operation is that multiple groups are executed alternately
        for(var i = gap; i < len; i++) {
            var j = i;
            var current = arr[i];
            while(j - gap >= 0 && current < arr[j - gap]) {
                 arr[j] = arr[j - gap];
                 j = j - gap;
            }
            arr[j] = current;
        }
    }
    return arr;
}

5. Merge Sort

function mergeSort(arr) {
    var len = arr.length;
    if(len < 2) {
        return arr;
    }
    var middle = Math.floor(len / 2),
        left = arr.slice(0, middle),
        right = arr.slice(middle);
    return merge(mergeSort(left), mergeSort(right));
}
 
function merge(left, right) {
    var result = [];
 
    while(left.length>0 && right.length>0) {
        if(left[0] <= right[0]) {
            result.push(left.shift());
        }else{
            result.push(right.shift());
        }
    }
 
    while(left.length)
        result.push(left.shift());
 
    while(right.length)
        result.push(right.shift());
 
    return result;
}

6. Quick Sort

function quickSort(arr, left, right) {
    var len = arr.length,
        partitionIndex,
        left =typeof left !='number'? 0 : left,
        right =typeof right !='number'? len - 1 : right;
 
    if(left < right) {
        partitionIndex = partition(arr, left, right);
        quickSort(arr, left, partitionIndex-1);
        quickSort(arr, partitionIndex+1, right);
    }
    return arr;
}
 
function partition(arr, left ,right) {    // Partition operation
    var pivot = left,                     // Set reference value (pivot)
        index = pivot + 1;
    for(var i = index; i <= right; i++) {
        if(arr[i] < arr[pivot]) {
            swap(arr, i, index);
            index++;
        }       
    }
    swap(arr, pivot, index - 1);
    return index-1;
}
 
function swap(arr, i, j) {
    var temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}

7. Heap Sort

var len;   // Because multiple functions declared need data length, set len as a global variable
 
function buildMaxHeap(arr) {  // Build large top reactor
    len = arr.length;
    for(var i = Math.floor(len/2); i >= 0; i--) {
        heapify(arr, i);
    }
}
 
function heapify(arr, i) {    // Heap adjustment
    var left = 2 * i + 1,
        right = 2 * i + 2,
        largest = i;
 
    if(left < len && arr[left] > arr[largest]) {
        largest = left;
    }
 
    if(right < len && arr[right] > arr[largest]) {
        largest = right;
    }
 
    if(largest != i) {
        swap(arr, i, largest);
        heapify(arr, largest);
    }
}
 
function swap(arr, i, j) {
    var temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}
 
function heapSort(arr) {
    buildMaxHeap(arr);
 
    for(var i = arr.length - 1; i > 0; i--) {
        swap(arr, 0, i);
        len--;
        heapify(arr, 0);
    }
    return arr;
}

8. Counting Sort

function countingSort(arr, maxValue) {
    var bucket =new Array(maxValue + 1),
        sortedIndex = 0;
        arrLen = arr.length,
        bucketLen = maxValue + 1;
 
    for(var i = 0; i < arrLen; i++) {
        if(!bucket[arr[i]]) {
            bucket[arr[i]] = 0;
        }
        bucket[arr[i]]++;
    }
 
    for(var j = 0; j < bucketLen; j++) {
        while(bucket[j] > 0) {
            arr[sortedIndex++] = j;
            bucket[j]--;
        }
    }
 
    return arr;
}

9. Bucket Sort

function bucketSort(arr, bucketSize) {
    if(arr.length === 0) {
      return arr;
    }
 
    var i;
    var minValue = arr[0];
    var maxValue = arr[0];
    for(i = 1; i < arr.length; i++) {
      if(arr[i] < minValue) {
          minValue = arr[i];               // Minimum value of input data
      }else if(arr[i] > maxValue) {
          maxValue = arr[i];               // Maximum value of input data
      }
    }
 
    // Initialization of bucket
    var DEFAULT_BUCKET_SIZE = 5;           // Set the default number of buckets to 5
    bucketSize = bucketSize || DEFAULT_BUCKET_SIZE;
    var bucketCount = Math.floor((maxValue - minValue) / bucketSize) + 1;  
    var buckets =new Array(bucketCount);
    for(i = 0; i < buckets.length; i++) {
        buckets[i] = [];
    }
 
    // The mapping function is used to allocate the data to each bucket
    for(i = 0; i < arr.length; i++) {
        buckets[Math.floor((arr[i] - minValue) / bucketSize)].push(arr[i]);
    }
 
    arr.length = 0;
    for(i = 0; i < buckets.length; i++) {
        insertionSort(buckets[i]);                     // Sort each bucket. Insert sort is used here
        for(var j = 0; j < buckets[i].length; j++) {
            arr.push(buckets[i][j]);                     
        }
    }
 
    return arr;
}

10. Radix Sort

var counter = [];
function radixSort(arr, maxDigit) {
    var mod = 10;
    var dev = 1;
    for(var i = 0; i < maxDigit; i++, dev *= 10, mod *= 10) {
        for(var j = 0; j < arr.length; j++) {
            var bucket = parseInt((arr[j] % mod) / dev);
            if(counter[bucket]==null) {
                counter[bucket] = [];
            }
            counter[bucket].push(arr[j]);
        }
        var pos = 0;
        for(var j = 0; j < counter.length; j++) {
            var value =null;
            if(counter[j]!=null) {
                while((value = counter[j].shift()) !=null) {
                      arr[pos++] = value;
                }
          }
        }
    }
    return arr;
}

Python coding case

array_list = [13, 27, 11, 18, 41, 25, 36, 29, -7, 111, 18, 33, -3]
# All n represents the number of local judgments, n_ Represents the number of local assignments, and all I represents the number of global judgments, i_ Indicates the number of global assignments.

1. Bubble Sort

def bubble(array):
    n = 0
    n_ = 0
    for _ in range(1, len(array)):  # TODO: for in the first layer indicates the number of times of the loop
        for __ in range(0, len(array) - _):  # TODO: the second layer, for, indicates which two elements to compare
            n += 1
            if array[__] > array[__ + 1]:  # TODO: if the front is greater than the rear
                n_ += 1
                array[__], array[__ + 1] = array[__ + 1], array[__]  # TODO: swap the positions of these two elements
    print(f'Bubble sorting co judgment {n} Once, perform the assignment {n_} Times.')
    return array


print(bubble(list(array_list)))

2. Selection Sort

def selection(array):
    n = 0
    n_ = 0
    for _ in range(len(array) - 1):  # TODO: for in the first layer indicates the number of times of the loop
        n_ += 1
        __ = _  # TODO: set the starting element as the minimum element
        for ___ in range(_ + 1, len(array)):  # TODO: the second layer, for, indicates that the smallest element and the following elements are compared one by one
            n += 1
            if array[__] > array[___]:  # TODO: if the current element is smaller than the smallest element
                n_ += 1
                __ = ___  # TODO: mark the current element angle as the smallest element angle
        n_ += 1
        array[_], array[__] = array[__], array[_]  # TODO: exchange the smallest element with the starting element after searching
    print(f'Select sort common judgment {n} Once, perform the assignment {n_} Times.')
    return array


print(selection(list(array_list)))

3. Insertion Sort

def insertion(array):
    n = 0
    n_ = 0
    for _ in range(1, len(array)):  # TODO: for in the first layer indicates the number of times of the loop
        n_ += 1
        __ = array[_]  # TODO: sets the current element to be inserted
        n += 1
        while _ and array[_ - 1] > __:  # TODO: when the comparison element is larger than the current element (at this time, the variable is used to mark the comparison element compared with the current element)
            n += 1
            n_ += 2
            array[_] = array[_ - 1]  # TODO: move comparison elements back
            _ -= 1  # TODO: select the next comparison element forward
        n_ += 1
        array[_] = __  # TODO: when the comparison element is smaller than the current element, insert the current element after it
    print(f'Insert sort common judgment {n} Once, perform the assignment {n_} Times.')
    return array


print(insertion(list(array_list)))

4. Shell Sort

def shell(array, sep=2):
    n = 0
    n_ = 0
    n_ += 1
    _ = len(array) // SEP # todo: round the calculated increment (interval) value
    n += 1
    while _:
        for __ in range(_, len(array)):  # TODO: traverse the comparison from the incremental value
            n_ += 1
            ___ = array[__]  # TODO: sets the current element to be inserted
            n += 1
            while __ - _ >= 0 and array[__ - _] > ___:  # TODO: when the comparison element is larger than the current element (at this time, the variable _ is used to mark the comparison element compared with the current element)
                n += 1
                n_ += 2
                array[__] = array[__ - _]  # TODO: move comparison elements back
                __ -= _  # TODO: select the next comparison element forward
            n_ += 1
            array[__] = ___  # TODO: when the comparison element is smaller than the current element, insert the current element after it
        n_ += 1
        _ //=SEP # todo: decrease the increment (interval) value
    print(f'Hill sort co judgment {n} Once, perform the assignment {n_} Times.')
    return array


print(shell(list(array_list)))

5. Merge Sort

i = 0
i_ = 0

# merge = lambda _: _ if len(_) == 1 else merge_sort(merge(_[:len(_) // 2]), merge(_[len(_) //  2: ]) # todo: sequence of numbers after dichotomy using recursive operation
# merge = lambda _: len(_) == 1 and _ or merge_sort(merge(_[:len(_) // 2]), merge(_[len(_) //  2: ]) # todo: sequence of numbers after dichotomy using recursive operation


def merge(array):
    global i, i_
    i += 1
    if len(array) < 2:
        return array
    i_ += 2
    return merge_sort(merge(array[:len(array) // 2] ), merge (array [len (array) / / 2:]) # todo: the sequence of numbers after dichotomy using recursive operation


def merge_sort(left, right):
    global i, i_
    i_ += 1
    _ = []  # TODO: sort and merge two series
    i += 1
    while left and right:  # TODO: both sequences have values
        i += 2
        i_ += 1
        # _.append((lambda _, __: _[0] <= __[0] and _.pop(0) or __.pop(0))(left, right))  # TODO: the first minimum of the left and right series is placed in front of [. Append ((lambda,). Pop (0) if [0] < =__ [0] else __. pop(0))(left, right)) ]
        if left[0] <= right[0]:  # TODO: the first minimum of the left and right series is placed in front
            _.append(left.pop(0))
        else:
            _.append(right.pop(0))
    i_ += 1
    _.extend(left and left or right)  # TODO: directly add [+ = left if left else right] as long as there are values in the sequence
    return _


_ = merge(list(array_list))
print(f'Merge sort co judgment {i} Once, perform the assignment {i_} Times.\n{_}')

6. Quick Sort

i = 0
i_ = 0


def quick(array):
    global i, i_
    i += 1
    if len(array) < 2:  # TODO: baseline condition: arrays that are empty or contain only one element are "ordered"
        return array
    i += 2 * len(array[1:])
    i_ += 2 * len(array[1:])
    return quick([_ for _ in array[1:] if _ <= array[0]]) + [array[0]] + quick([_ for _ in array[1:] if _ > array[0]])  # TODO: regroup subarray composed of all elements less than or equal to, benchmark elements and elements greater than benchmark value (recursive condition)


_ = quick(list(array_list))
print(f'Quick sort co judgment {i} Once, perform the assignment {i_} Times.\n{_}')

7. Heap Sort

i = 0
i_ = 0


def heap(array):
    global i, i_
    for _ in range(len(array) // 2, -1, -1):
        array = heap_sort(array, _, len(array))  # TODO: adjust the structure from the first non leaf node from bottom to top and from right to left (build a large top heap)
    for __ in range(len(array) - 1, 0, -1):
        i_ += 1
        array[0], array[__] = array[__], array[0]  # TODO: swap top and end elements
        array = heap_sort(array, 0, __)  # TODO: readjust the heap (sort the last element when looping)
    return array


def heap_sort(array, _, __):  # TODO: heap adjustment
    global i, i_
    ___ = _
    i += 1
    if 2 * _ + 1 < __ and array[2 * _ + 1] > array[___]:  # TODO: find a larger child node (when the left child node is larger)
        i_ += 1
        ___ = 2 * _ + 1
    i += 1
    if 2 * _ + 2 < __ and array[2 * _ + 2] > array[___]:  # TODO: find a larger child node (when the right child node is larger)
        i_ += 1
        ___ = 2 * _ + 2
    i += 1
    if ___ != _:  # TODO: recurse again if the heap item is adjusted
        i_ += 2
        array[_], array[___] = array[___], array[_]  # TODO: swap top and end elements
        heap_sort(array, ___, __)  # TODO: readjust the heap
    return array


_ = heap(list(array_list))
print(f'Heap sort common judgment {i} Once, perform the assignment {i_} Times.\n{_}')

8. Counting Sort

def counting(array):
    n = 0
    n_ = 0
    n_ += 1 + 2 * (max(array) - min(array))
    _ = [0] * len(array)  # TODO: store the sorted array
    __ = [array.count(_) for _ in range(min(array), max(array) + 1)]  # TODO: through subscript index, which numbers are there in the number of records and how many have the same value
    __ = [sum(__[:_]) for _ in range(1, len(__) + 1)]  # TODO: the number of numbers smaller than a certain number in the array, which is used for sorting
    for ___ in array[::-1]:
        n_ += 3
        ___ -= min(array)  # TODO: optimize the relationship between negative numbers and subscripts so that the minimum negative subscript is exactly 0
        _[__[___] - 1] = ___ + min(array)  # TODO: the subscript values are in order to restore the optimization of the relationship between negative numbers and subscripts
        __[___] -= 1  # TODO: each time a number is inserted, the current subscript is subtracted by one
    print(f'Count sort common judgment {n} Once, perform the assignment {n_} Times.')
    return _


print(counting(list(array_list)))

9. Bucket Sort

def bucket(array):
    n = 0
    n_ = 0
    n_ += max(array) - min(array) + 1
    _ = []  # TODO: store the sorted array
    __ = [array.count(_) for _ in range(min(array), max(array) + 1)]  # TODO: through subscript index, which numbers are there in the number of records and how many have the same value
    for ___, ____ in enumerate(__):
        for _____ in range(____):  # TODO: perform the number of occurrences (optimization of count sorting)
            n_ += 1
            _.append(___ + min(array))  # TODO: the subscript values are in order to restore the optimization of the relationship between negative numbers and subscripts
    print(f'Bucket sorting common judgment {n} Once, perform the assignment {n_} Times.')
    return _


print(bucket(list(array_list)))

10. Radix Sort

def radix(array):
    n = 0
    n_ = 0
    n_ += len(array)
    _ = [__ - min(array) for __ in array]  # TODO: optimize the relationship between negative numbers and subscripts so that the minimum negative subscript is exactly 0, and construct an array without negative numbers
    for __ in range(len(str(max(_)))):  # TODO: do multi round operation according to the maximum digital length, from one digit to ten digit to hundred digit
        n_ += 10
        ____ = [[] for _ in range(10)]  # TODO: since each digit is 0-9, 10 barrels are created
        for ___ in _:
            n_ += 1
            ____[int(___ / (10 ** __) % 10)].append(___)  # TODO: by one digit, ten digit, hundred digit Put it in the bucket
        n_ += 1
        _ = [___ for __ in ____ for ___ in __]  # TODO: rearrange the list in the order of the current bucket
    print(f'Cardinality sorting common judgment {n} Once, perform the assignment {n_} Times.')
    return [__ + min(array) for __ in _]


print(radix(list(array_list)))

Top ten classic sorting classes in Python

Note: in the above coding case, the judgment and assignment times of each sorting method are mainly counted to represent the detailed data. The next class can judge the execution time of the whole sorting and macroscopically represent the execution speed of each function, Sort with the existing default value (the maximum recursion depth is set to 10000, and the number of 5000 in the list is selected from - 2000 ~ 2000), so that almost every sort will be useful and there will be no stack overflow for my computer.

import time
time_show = True  # Show execution time


# Calculate function runtime
def calc_time(decorator):
    def calc(function=None, *arg, **kwargs):
        if time_show:
            start = time.time()
            fun = decorator(function, *arg, **kwargs)
            print(f'{decorator.__name__} Function execution time:{time.time() - start:.3f}')
            return fun
        else:
            return decorator(function, *arg, **kwargs)
    return calc


# A decorator function that generally handles the correctness of numeric list values. If the incoming value array is valid, the instance property array will be replaced
def check(function):
    def num_array_check(self: object = None, array: list = None, *args: tuple, **kwargs: dict):
        if array and isinstance(array, list) and set([type(a) for a in array]).issubset({int, float}):
            self.array = array
        elif hasattr(self, 'array'):
            if self.array:
                array = self.array
            else:
                raise ValueError("The valid list value is empty !")
        else:
            self.array = []
            array = []
        return function(self, array, *args, **kwargs)
    return num_array_check


class Sort:
    @check
    # Digital list selective initialization
    def __init__(self, array: list = None):
        self.array = array

    @check
    @calc_time
    # Bubble Sort
    def bubble(self, array: list = None):
        for _ in range(1, len(array)):  # TODO: for in the first layer indicates the number of times of the loop
            for __ in range(0, len(array) - _):  # TODO: the second layer, for, indicates which two elements to compare
                if array[__] > array[__ + 1]:  # TODO: if the front is greater than the rear
                    array[__], array[__ + 1] = array[__ + 1], array[__]  # TODO: swap the positions of these two elements
        return array

    @check
    @calc_time
    # Selection Sort
    def selection(self, array: list = None):
        for _ in range(len(array) - 1):  # TODO: for in the first layer indicates the number of times of the loop
            __ = _  # TODO: set the starting element as the minimum element
            for ___ in range(_ + 1, len(array)):  # TODO: the second layer, for, indicates that the smallest element and the following elements are compared one by one
                if array[__] > array[___]:  # TODO: if the current element is smaller than the smallest element
                    __ = ___  # TODO: mark the current element angle as the smallest element angle
            array[_], array[__] = array[__], array[_]  # TODO: exchange the smallest element with the starting element after searching
        return array

    @check
    @calc_time
    # Insertion Sort
    def insertion(self, array: list = None):
        for _ in range(1, len(array)):  # TODO: for in the first layer indicates the number of times of the loop
            __ = array[_]  # TODO: sets the current element to be inserted
            while _ and array[_ - 1] > __:  # TODO: when the comparison element is larger than the current element (at this time, the variable is used to mark the comparison element compared with the current element)
                array[_] = array[_ - 1]  # TODO: move comparison elements back
                _ -= 1  # TODO: select the next comparison element forward
            array[_] = __  # TODO: when the comparison element is smaller than the current element, insert the current element after it
        return array

    @check
    @calc_time
    # Shell Sort
    def shell(self, array: list = None, sep: int = 2):
        if not isinstance(sep, int):
            sep = 2
        _ = len(array) // SEP # todo: round the calculated increment (interval) value
        while _:
            for __ in range(_, len(array)):  # TODO: traverse the comparison from the incremental value
                ___ = array[__]  # TODO: sets the current element to be inserted
                while __ - _ >= 0 and array[__ - _] > ___:  # TODO: when the comparison element is larger than the current element (at this time, the variable _ is used to mark the comparison element compared with the current element)
                    array[__] = array[__ - _]  # TODO: move comparison elements back
                    __ -= _  # TODO: select the next comparison element forward
                array[__] = ___  # TODO: when the comparison element is smaller than the current element, insert the current element after it
            _ //=SEP # todo: decrease the increment (interval) value
        return array

    @check
    @calc_time
    # Merge Sort - 1
    def merge(self, array: list = None):
        return self.__merge(array)

    # Merge Sort - 2
    def __merge(self, array: list = None):
        if len(array) < 2:
            return array
        return self.__merge_sort(self.__merge(array[:len(array) // 2]), self.__ Merge (array [len (array) / / 2:]) # todo: the sequence of numbers after dichotomy using recursive operation

    @staticmethod
    # Merge Sort - 3
    def __merge_sort(left, right):
        _ = []  # TODO: sort and merge two series
        while left and right:  # TODO: both sequences have values
            if left[0] <= right[0]:  # TODO: the first minimum of the left and right series is placed in front
                _.append(left.pop(0))
            else:
                _.append(right.pop(0))
        _.extend(left and left or right)  # TODO: directly add [+ = left if left else right] as long as there are values in the sequence
        return _

    @check
    @calc_time
    # Quick Sort - 1
    def quick(self, array: list = None):
        return self.__quick(array)

    # Quick Sort - 2
    def __quick(self, array: list = None):
        if len(array) < 2:  # TODO: baseline condition: arrays that are empty or contain only one element are "ordered"
            return array
        return self.__quick([_ for _ in array[1:] if _ <= array[0]]) + [array[0]] + self.__quick([_ for _ in array[1:] if _ > array[0]])  # TODO: regroup subarray composed of all elements less than or equal to, benchmark elements and elements greater than benchmark value (recursive condition)

    @check
    @calc_time
    # Heap Sort -- 1
    def heap(self, array: list = None):
        for _ in range(len(array) // 2, -1, -1):
            array = self.__heap_sort(array, _, len(array))  # TODO: adjust the structure from the first non leaf node from bottom to top and from right to left (build a large top heap)
        for __ in range(len(array) - 1, 0, -1):
            array[0], array[__] = array[__], array[0]  # TODO: swap top and end elements
            array = self.__heap_sort(array, 0, __)  # TODO: readjust the heap (sort the last element when looping)
        return array

    # Heap Sort -- 2
    def __heap_sort(self, array, _, __):  # TODO: heap adjustment
        ___ = _
        if 2 * _ + 1 < __ and array[2 * _ + 1] > array[___]:  # TODO: find a larger child node (when the left child node is larger)
            ___ = 2 * _ + 1
        if 2 * _ + 2 < __ and array[2 * _ + 2] > array[___]:  # TODO: find a larger child node (when the right child node is larger)
            ___ = 2 * _ + 2
        if ___ != _:  # TODO: recurse again if the heap item is adjusted
            array[_], array[___] = array[___], array[_]  # TODO: swap top and end elements
            self.__heap_sort(array, ___, __)  # TODO: readjust the heap
        return array

    @check
    @calc_time
    # Counting Sort
    def counting(self, array: list = None):
        _ = [0] * len(array)  # TODO: store the sorted array
        __ = [array.count(_) for _ in range(min(array), max(array) + 1)]  # TODO: through subscript index, which numbers are there in the number of records and how many have the same value
        __ = [sum(__[:_]) for _ in range(1, len(__) + 1)]  # TODO: the number of numbers smaller than a certain number in the array, which is used for sorting
        for ___ in array[::-1]:
            ___ -= min(array)  # TODO: optimize the relationship between negative numbers and subscripts so that the minimum negative subscript is exactly 0
            _[__[___] - 1] = ___ + min(array)  # TODO: the subscript values are in order to restore the optimization of the relationship between negative numbers and subscripts
            __[___] -= 1  # TODO: each time a number is inserted, the current subscript is subtracted by one
        return _

    @check
    @calc_time
    # Bucket Sort
    def bucket(self, array: list = None):
        _ = []  # TODO: store the sorted array
        __ = [array.count(_) for _ in range(min(array), max(array) + 1)]  # TODO: through subscript index, which numbers are there in the number of records and how many have the same value
        for ___, ____ in enumerate(__):
            for _____ in range(____):  # TODO: perform the number of occurrences (optimization of count sorting)
                _.append(___ + min(array))  # TODO: the subscript values are in order to restore the optimization of the relationship between negative numbers and subscripts
        return _

    @check
    @calc_time
    # Radix Sort
    def radix(self, array: list = None):
        _ = [__ - min(array) for __ in array]  # TODO: optimize the relationship between negative numbers and subscripts so that the minimum negative subscript is exactly 0, and construct an array without negative numbers
        for __ in range(len(str(max(_)))):  # TODO: do multi round operation according to the maximum digital length, from one digit to ten digit to hundred digit
            ____ = [[] for _ in range(10)]  # TODO: since each digit is 0-9, 10 barrels are created
            for ___ in _:
                ____[int(___ / (10 ** __) % 10)].append(___)  # TODO: by one digit, ten digit, hundred digit Put it in the bucket
            _ = [___ for __ in ____ for ___ in __]  # TODO: rearrange the list in the order of the current bucket
        return [__ + min(array) for __ in _]


if __name__ == '__main__':
    import sys
    import random
    time_show = True  # Show execution time
    # Set the maximum recursion depth. The default maximum recursion is 1000 times. After setting the maximum recursion depth, the effective recursion depth is related to python version, cpu performance, operating system, etc
    sys.setrecursionlimit(10000)
    # array_list = [13, 27, 11, 18, 41, 25, 36, 29, -7, 111, 18, 33, -3]
    array_list = [random.randint(-2000, 2000) for _ in range(5000)]
    print('List to sort')
    print(array_list)
    print(f'Length of list to be sorted:{len(array_list)}')
    s = Sort(array_list)
    s.bubble()
    s.selection()
    s.insertion()
    s.shell()
    s.merge()
    s.quick()
    s.heap()
    s.counting()
    s.bucket()
    s.radix()
    # print(s.bubble())
    # print(s.selection())
    # print(s.insertion())
    # print(s.shell())
    # print(s.merge())
    # print(s.quick())
    # print(s.heap())
    # print(s.counting())
    # print(s.bucket())
    # print(s.radix())

test result

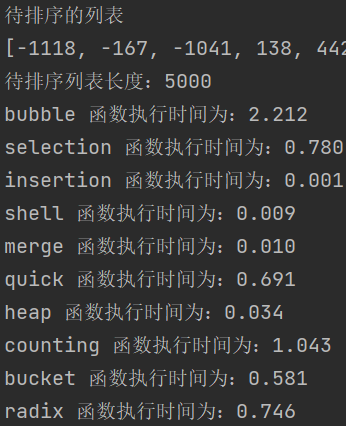
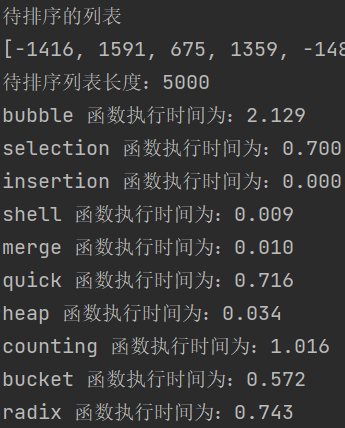
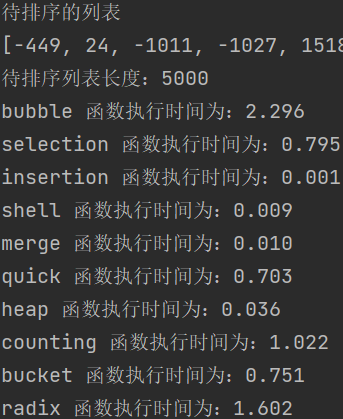
After three times of execution, it can be found that insertion sorting consumes almost no time, followed by Hill sorting and merge sorting. Bubble sorting is almost the most troublesome, and cardinal sorting is almost the most unstable.

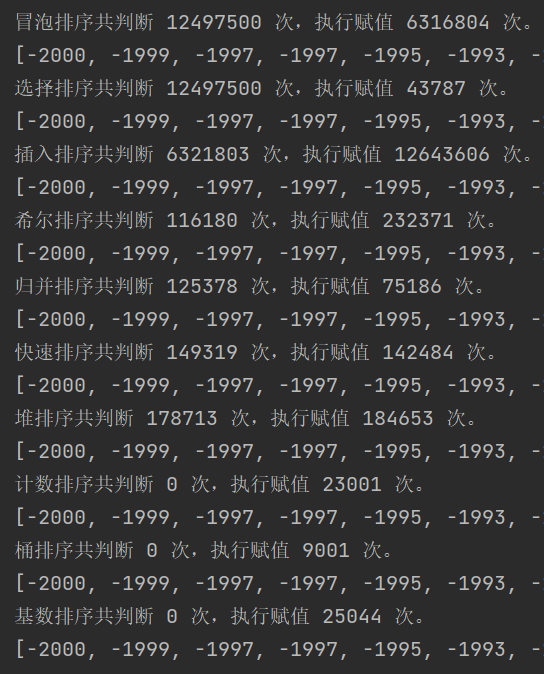
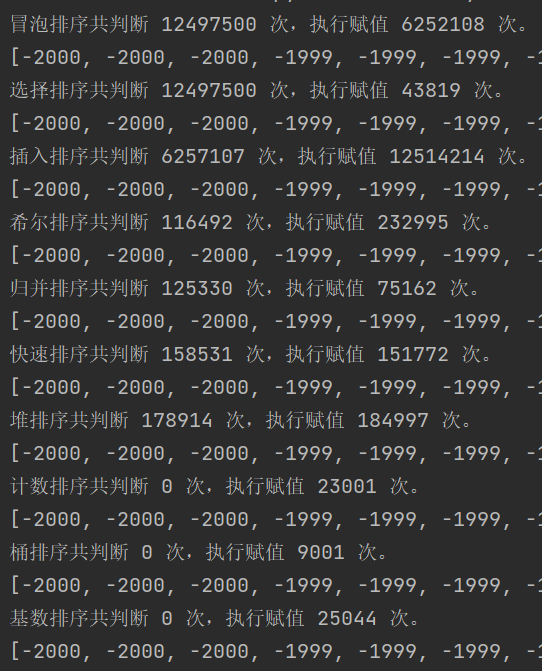
Look at the judgment of the number of assignment times. It has been executed twice here. Of course, it is not accurate, because I can see that the assignment in the list derivation is not included. Otherwise, the execution times of the last three non comparison sorting are so few, and it may take so long. We can see that the insertion sort assignment times are the most, and the guess assignment operation here takes almost no time.

Conclusion

This is the last and longest blog I published this year (2021). I'm not familiar with JavaScript, so I didn't test JavaScript, so I took Python for surgery. This blog is over. I hope those I like can connect three times with one key. I wish you a happy new year in advance!