-
The maximum degree of each node is 2 (up to 2 subtrees)
-
The left subtree and the right subtree are ordered, and the binary tree is an ordered tree
-
Even if a node has only one subtree, it is necessary to distinguish between the left and right subtrees
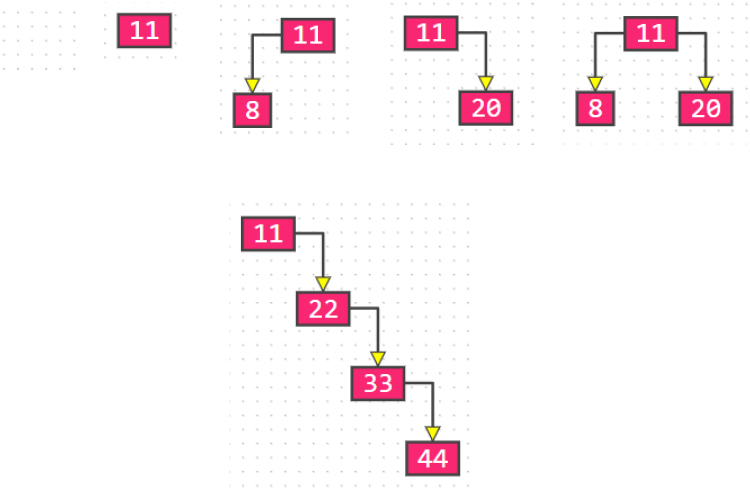
The i-th layer of non empty binary tree has at most 2i − 1 nodes (I ≥ 1)
There are at most 2h-1 nodes (H ≥ 1) on the binary tree with height H
For any non empty binary tree, if the number of leaf nodes is n0 and the number of nodes with degree 2 is n2, there are: n0 = n2 + 1
-
Assuming that the number of nodes with degree 1 is n1, the total number of nodes in the binary tree n = n0 + n1 + n2
-
Number of edges of binary tree T = n1 + 2 * n2 = n – 1 = n0 + n1 + n2 – 1
-
So n0 = n2 + 1
===========================================================================================
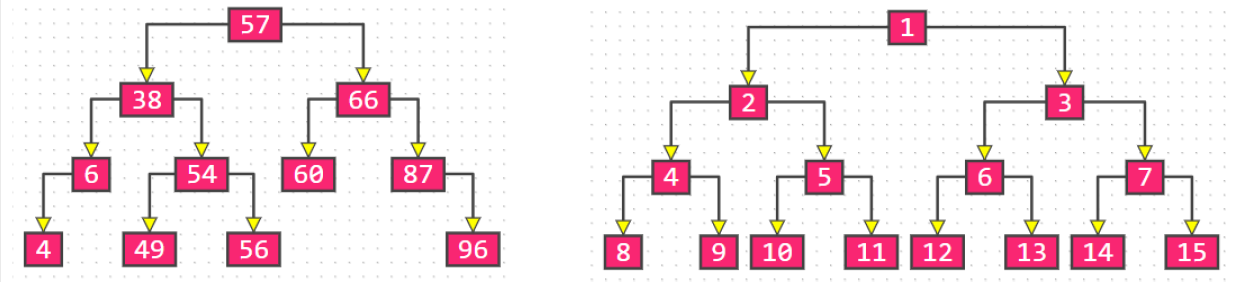
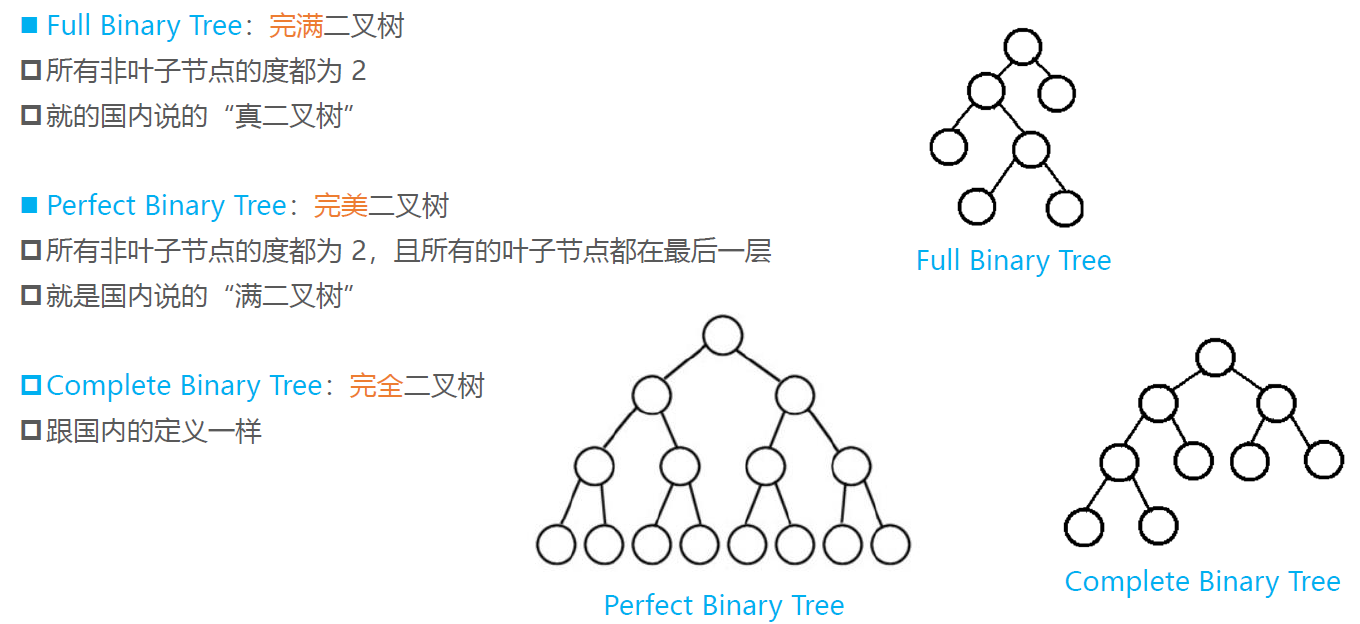
True binary tree: the degree of all nodes is either 0 or 2
The following figure is not a true binary tree:
=========================================================================================
Full binary tree: the degree of nodes in the last layer is 0, and the degree of other nodes is 2
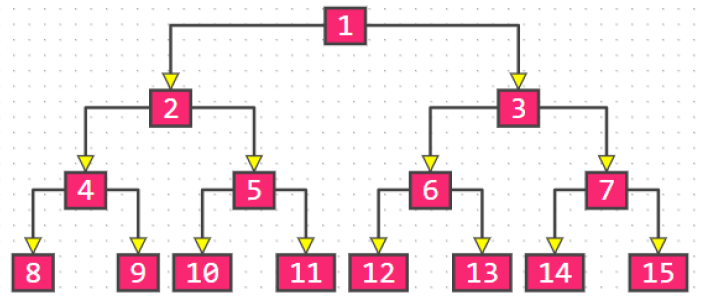
Assuming that the height of the full binary tree is h (H ≥ 1), then
-
Number of nodes in layer i: 2i − 1
-
Number of leaf nodes: 2h − 1
-
Total number of nodes n
- n = 2h − 1 = 20 + 21 + 22 + ⋯ + 2h−1
-
Relationship between tree height and total nodes: h = log2(n + 1)
In the same height binary tree, the full binary tree has the largest number of leaf nodes and the largest number of total nodes;
A full binary tree must be a true binary tree, and a true binary tree is not necessarily a full binary tree;
==============================================================================================
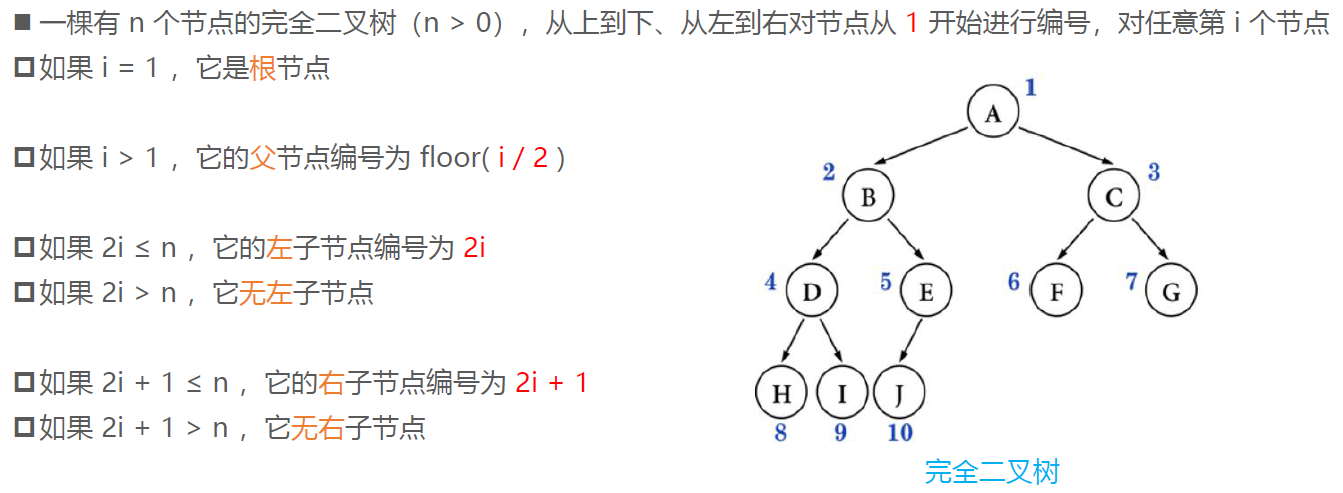
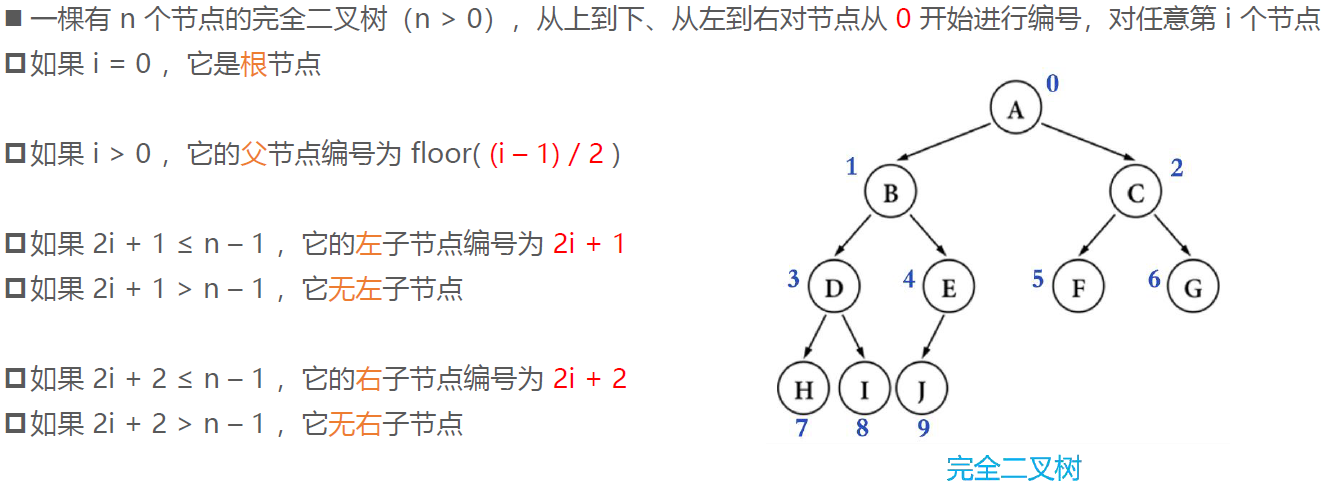
Complete binary tree: number nodes from top to bottom and from left to right. All numbers can correspond to those in the full binary tree with the same height
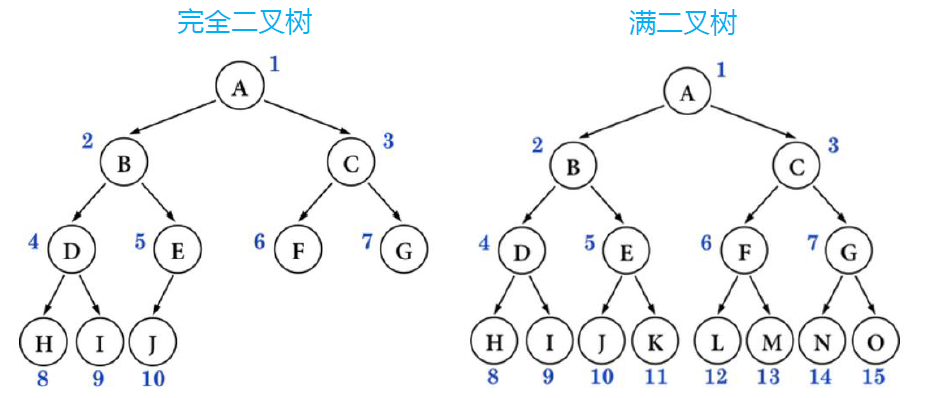
Properties of complete binary tree
-
The node with degree 1 has only the left subtree
-
Nodes with degree 1 are either 1 or 0
-
For a binary tree with the same number of nodes, the height of a complete binary tree is the smallest
-
Assuming that the height of the complete binary tree is h (H ≥ 1), then:
-
At least 2h − 1 node (20 + 21 + 22 +... + 2h − 2 + 1)
-
At most 2h − 1 node (20 + 21 + 22 +... + 2h − 1, i.e. full binary tree)
-
The total number of nodes is n
2h−1 ≤ n < 2h
h − 1 ≤ log2n < h
h = floor( log2n ) + 1
(floor is rounded down and ceiling is rounded up)
-
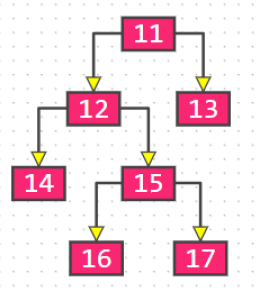
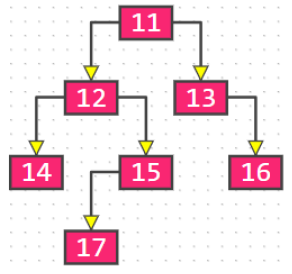
The following figure is not a complete binary tree:
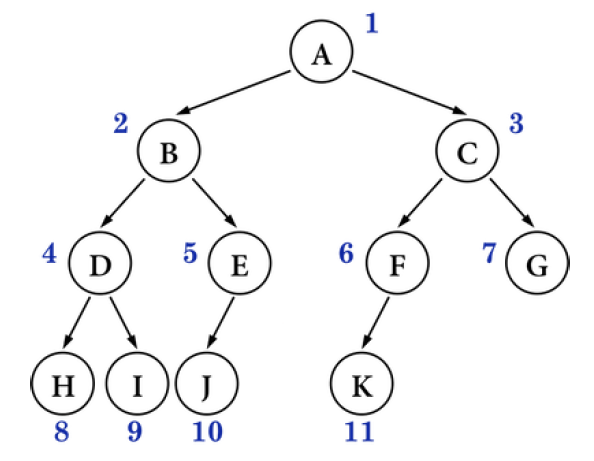
Interview questions (complete binary tree)

What foreign textbooks say: find out
Traversal of binary tree + Exercise
===============================================================================
Traversal is a common operation in data structures: access all elements once;
The traversal of linear data structure is relatively simple:
-
Positive order ergodic
-
Reverse traversal
According to the different access order of nodes, there are four common traversal methods of binary tree:
-
Preorder Traversal
-
Inorder Traversal
-
Postorder Traversal
-
Level Order Traversal
Traversal application:
-
Preorder traversal: display of tree structure (pay attention to the order of left and right subtrees)
-
Middle order traversal: the middle order traversal of binary search tree processes nodes in ascending or descending order
-
Post order traversal: it is applicable to some operations from child to parent
-
Sequence traversal: calculate the height of a binary tree and judge whether a tree is a complete binary tree
Access order: root node, pre order traversal of left subtree, pre order traversal of right subtree
The results of the preorder traversal in the following figure are: 7, 4, 2, 1, 3, 5, 9, 8, 11, 10, 12
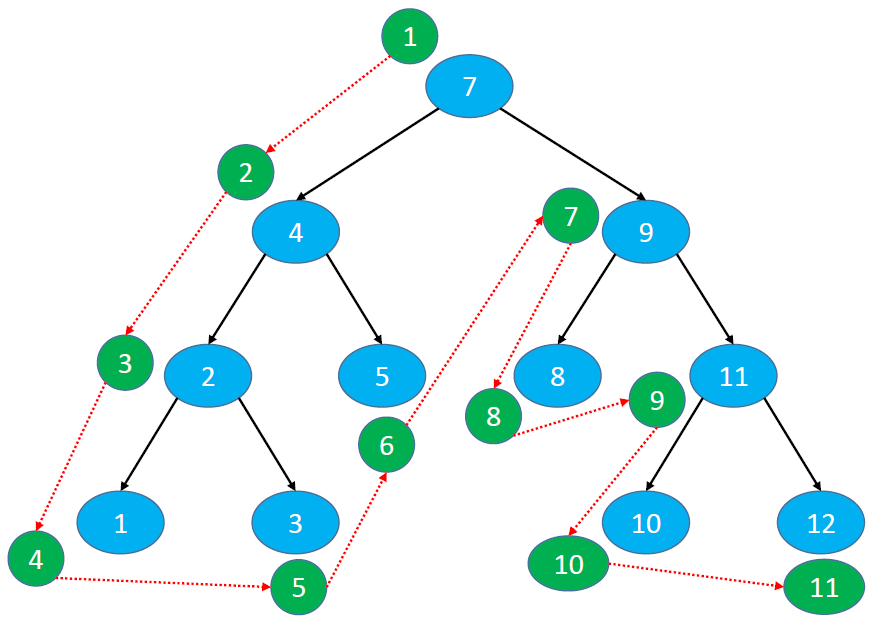
Preorder traversal of binary tree: https://leetcode-cn.com/problems/binary-tree-preorder-traversal/
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
List<Integer> list = new ArrayList<>();
public List<Integer> preorderTraversal(TreeNode root) {
if(root == null) return list;
list.add(root.val);
preorderTraversal(root.left);
preorderTraversal(root.right);
return list;
}
}
Access order: middle order traversal of left subtree, root node and middle order traversal of right subtree
The results of sequence traversal in the following figure are: 1, 2, 3, 4, 5, 7, 8, 9, 10, 11 and 12
Another medium order traversal access order: medium order traversal right subtree, root node, medium order traversal left subtree
The results of the middle order traversal in the following figure are: 12, 11, 10, 9, 8, 7, 5, 4, 3, 2 and 1
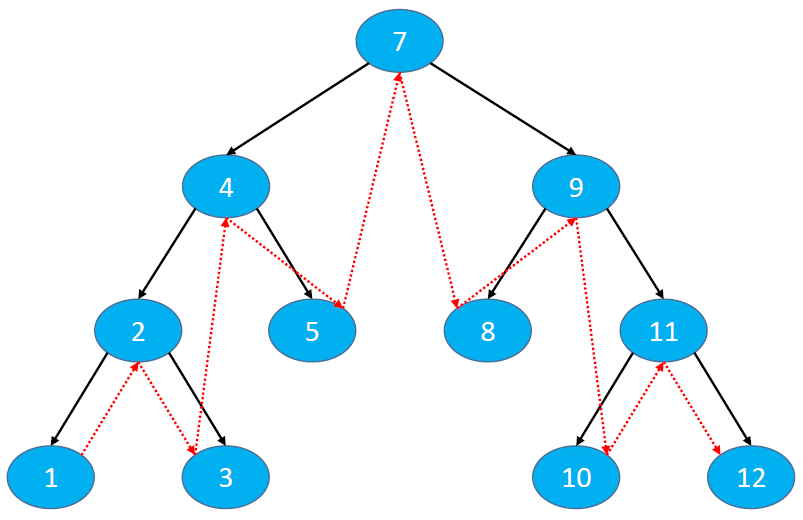
The middle order traversal results of binary search tree are in ascending or descending order;
Middle order traversal of binary tree: https://leetcode-cn.com/problems/binary-tree-inorder-traversal/
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
List<Integer> list = new ArrayList<>();
public List<Integer> inorderTraversal(TreeNode root) {
if(root == null) return list;
inorderTraversal(root.left);
list.add(root.val);
inorderTraversal(root.right);
return list;
}
}
Access order: traversing the left subtree, the right subtree and the root node
The results of post order traversal in the following figure are: 1, 3, 2, 5, 4, 8, 10, 12, 11, 9 and 7
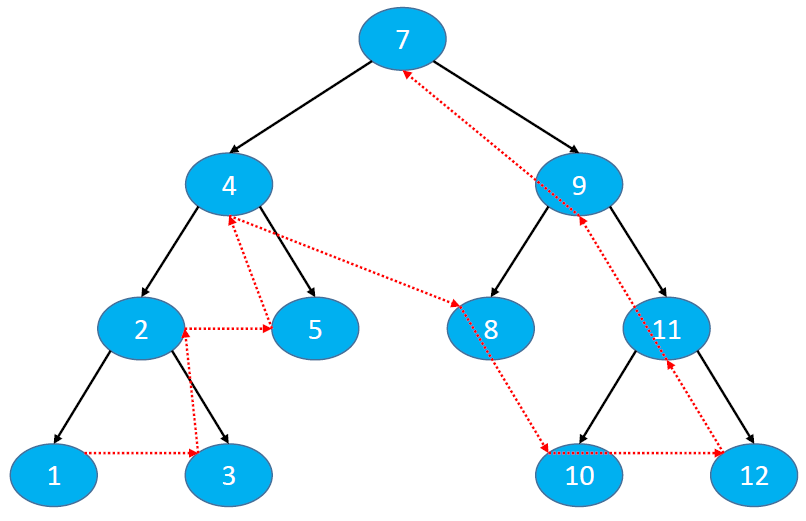
Post order traversal of binary tree: https://leetcode-cn.com/problems/binary-tree-postorder-traversal/
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
List<Integer> list = new ArrayList<Integer>();
public List<Integer> postorderTraversal(TreeNode root) {
if(root == null) return list;
postorderTraversal(root.left);
postorderTraversal(root.right);
list.add(root.val);
return list;
}
}
Access order: access each node from top to bottom and from left to right
The sequence traversal results in the figure below are: 7, 4, 9, 2, 5, 8, 11, 1, 3, 10 and 12
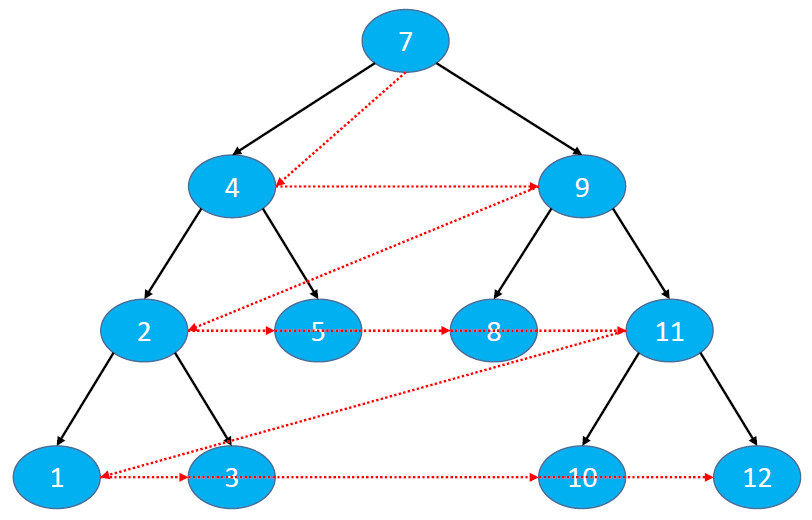
Hierarchical traversal of binary tree: https://leetcode-cn.com/problems/binary-tree-level-order-traversal/
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
List<List<Integer>> resList = new ArrayList<>();
public List<List<Integer>> levelOrder(TreeNode root) {
if(root == null) return resList;
Queue<TreeNode> queue = new LinkedList<>();
int levelSize = 1;
queue.offer(root);
List<Integer> list = new ArrayList<>(); ;
while(!queue.isEmpty()){
TreeNode node = queue.poll();
list.add(node.val);
levelSize--;
if(node.left != null){
queue.offer(node.left);
}
if(node.right != null){
queue.offer(node.right);
}
if(levelSize == 0){
resList.add(list);
levelSize = queue.size();
list = new ArrayList<>();
}
}
return resList;
}
}
Reconstruct the binary tree according to the traversal results
==============================================================================
The following results can ensure the reconstruction of a unique binary tree:
-
Preorder traversal + inorder traversal
-
Post order traversal + middle order traversal
Pre sequence traversal + Post sequence traversal:
-
If it is a true binary tree, the result is unique
-
Otherwise, the result is not unique
Pre order traversal + middle order traversal to reconstruct binary tree
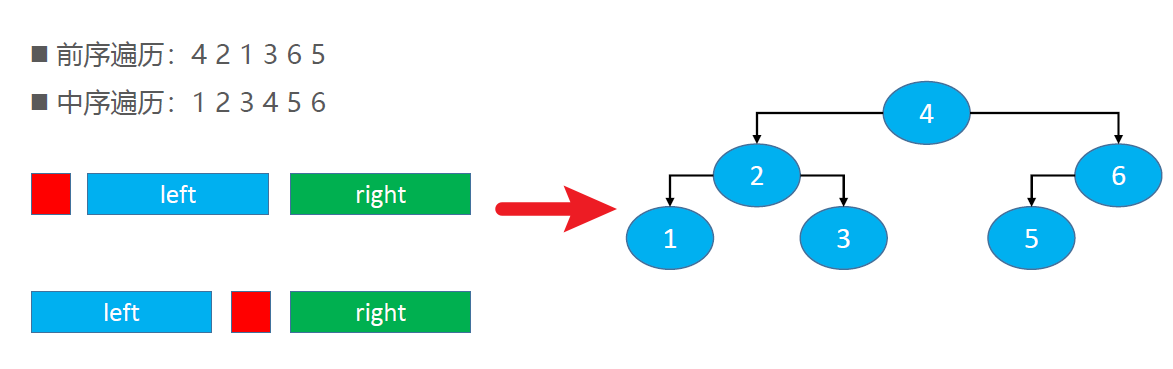
=======================================================================
The expressions of the four operations can be divided into three types:
-
prefix expression, also known as Polish expression
-
infix expression
-
postfix expression, also known as inverse Polish expression

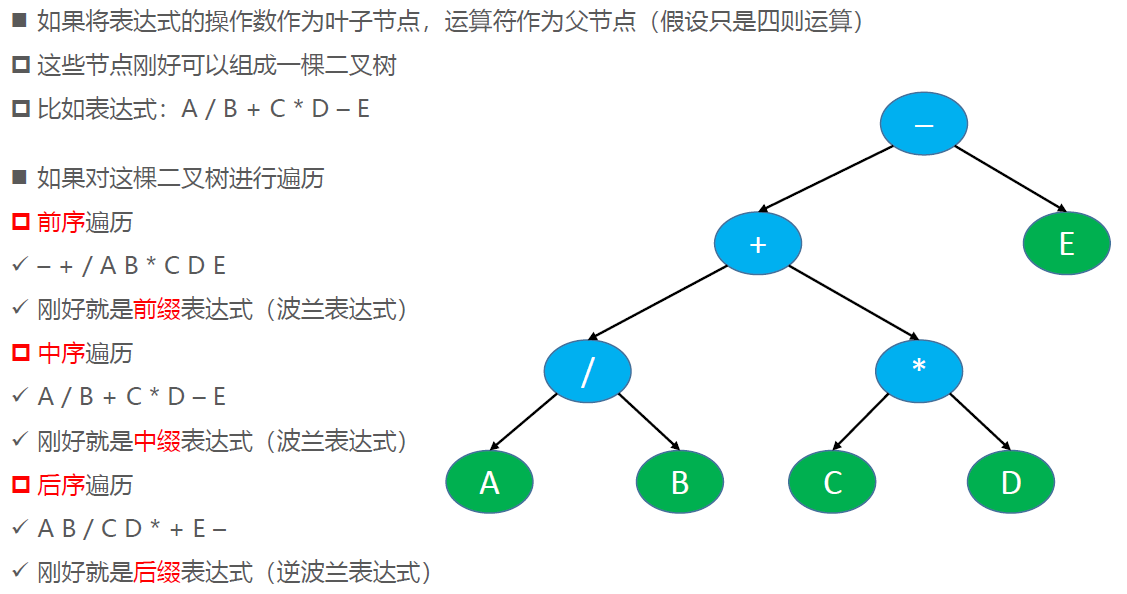
=====================================================================
226_ Flip binary tree: https://leetcode-cn.com/problems/invert-binary-tree/


/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }