Forward, middle, and backward traversal of binary trees (non-recursive implementation)
We have mentioned three ways of traversing a binary tree, the first, the second, and the second. Today we will do this non-recursively.
1. Pre-order traversal
We need stacks as a data structure for recursion
1.1 Analysis
- First we stack the root node
- Loop the top element out of the stack at the same time and add the top element to the result set
- Determine if the right child of the current node is empty, not empty on the stack
- Determine if the left child of the current node is empty, not empty on the stack
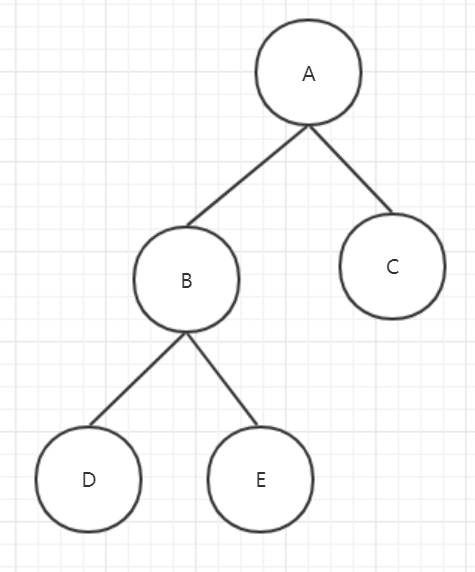
1.2 Example
Here's a specific example, illustrated by the following figure
First we put root node A on the stack, then we go into a loop
- Print A First
- Next, determine if their right child (C) is empty, find that it is not empty, and stack it
- Next, determine if their left child (B) is empty, find that it is not empty, and stack it
Second Enter Cycle
- Take top element B, print B
- Next, determine if their right child (E) is empty, find that it is not empty, and stack it
- Next, determine if their left child (D) is empty, find that it is not empty, and stack it
Third Enter Cycle
- Take top element D, print D
- Next, it determines if its right child (null) is empty and finds it empty
- Next, it determines if its left child (null) is empty and finds it empty
Fourth Enter Cycle
- Take top element E, print E
- Next, it determines if its right child (null) is empty and finds it empty
- Next, it determines if its left child (null) is empty and finds it empty
Fifth Enter Cycle
- Take top element C, print C
- Next, it determines if its right child (null) is empty and finds it empty
- Next, it determines if its left child (null) is empty and finds it empty
The loop ends, and the results are printed in turn: A B D E C
3. Code implementation
public List<Integer> preorderTraversal4(TreeNode root)
{
ArrayList<Integer> list = new ArrayList<>();
Stack<TreeNode> stack = new Stack<>();
if (root == null)
{
return list;
}
//First put the root node on the stack
stack.push(root);
//Loop judgment when stack is not empty
while (!stack.isEmpty())
{
//Pop-up top element
TreeNode cur = stack.pop();
//Add its value to the list collection
list.add(cur.val);
//If the right child of the current node is not empty, stack it
if (cur.right != null)
{
stack.push(cur.right);
}
//If the left child of the current node is not empty, stack it
if (cur.left != null)
{
stack.push(cur.left);
}
}
return list;
}
2. Medium-order traversal
2.1 Analysis
- Starting from the root node, lookup the left subtree in turn with a loop, and all elements encountered are stacked until empty, exiting the loop
- After reaching the leftmost element, take the top element out of the stack and add it to the result set
- Use the right subtree of the top element of the stack as the starting point, loop left again, and all the elements on the path are stacked
2.2 Example
Here's a specific example, illustrated by the following figure

-
First, we use a loop to go all the way to the left subtree until it is empty, then stack the A B D ** (stack: A B D at this time)**
-
Next, take the top element D of the stack and print D (in this case, stack: A B)
-
null right subtree of top stack element D as starting point, found empty
-
Next, take the top element B of the stack and print B (in this case, stack: A)
-
Start with the right subtree E of top element B and place it on the stack** (stack: A E at this time)**
-
Next, take the top element E and print E (stack: A at this point)
-
null, the right subtree of element E at the top of the stack, as the starting point, is found to be empty
-
Next take top element A and print A** (the stack is empty at this time)**
-
Use the right subtree C of element A at the top of the stack as the starting point and place it on the stack (stack: C in this case)
-
Next take the top element C and print C (the stack is empty at this time)
End of stack empty
2.3 Code
public List<Integer> inorderTraversal2(TreeNode root)
{
ArrayList<Integer> list = new ArrayList<>();
if (root == null)
{
return list;
}
Stack<TreeNode> stack = new Stack<>();
TreeNode cur = root;
while (true)
{
//Loop through to the left until empty
while (cur != null)
{
stack.push(cur);
cur = cur.left;
}
//2. If empty, end of traversal
if (stack.isEmpty())
{
break;
}
//3. Take the top element of the stack and access it
TreeNode pop = stack.pop();
list.add(pop.val);
//4. Start from the right subtree of the current node
cur = pop.right;
}
return list;
}
3. Post-order traversal
3.1 Analysis
- Starting from the root node, lookup the left subtree in turn with a loop, and all elements encountered are stacked until empty, exiting the loop
- Determine if the top element of the stack (peek is not pop) is accessible (in two cases)
- The top element of the stack has no right subtree, pop it
- The right subtree of the top element of the stack has been visited once and pop ped
- Use the right subtree of the top element of the stack as the starting point, loop left again, and all the elements on the path are stacked
3.2 Example
Here's a specific example, illustrated by the following figure

- First, we use a loop to look all the way to the left subtree until it is empty, then stack the A B D (in this case, stack: A B D)
- Next, determine the top element D of the stack, find that it has no right subtree, and print it out of the stack
- null right subtree of top stack element D as starting point, found empty
- Next, determine element B at the top of the stack and find that it has a right subtree, but it has not been visited yet. Use its right subtree as a starting point to start looping left into the stack (stack: A B E at this time)
- Next, determine the top element E, find that it has no right subtree, take it out of the stack and print it
- Next, determine the top element B** (second visit)** and find that it has a right subtree, but has been visited, stack it and print it (stack: A at this time)
- Next, determine element A at the top of the stack and find that it has a right subtree, but it has not been visited yet. Use its right subtree as a starting point to start looping left into the stack (stack: A C at this time)
- Next, determine the top element C of the stack, find that it has no right subtree, and print it out of the stack (stack: A in this case)
- Next, determine the top element A** (second visit)** and find that it has a right subtree, but has been visited, stack it and print it (the stack is empty at this time)
- End
3.3 Code
public List<Integer> postorderTraversal(TreeNode root)
{
ArrayList<Integer> list = new ArrayList<>();
if (root == null)
{
return list;
}
Stack<TreeNode> stack = new Stack<>();
TreeNode cur = root;
TreeNode pre = null;
while (true)
{
//1. Search left and stack until empty
while (cur != null)
{
stack.push(cur);
cur = cur.left;
}
if (stack.isEmpty())
{
break;
}
//Take out the top element of the stack and check if you can access it
TreeNode top = stack.peek();
//Two conditions to judge
if (top.right == null || pre == top.right)
{
TreeNode pop = stack.pop();
list.add(pop.val);
//The last record after the element has been traversed
pre = pop;
}
//If the condition is not satisfied, use the right subtree of the top element of the stack as the starting point, loop left again, and all the elements on the path are stacked
else
{
cur = top.right;
}
}
return list;
}