A few basic python grammar topics have been posted earlier, which are mainly used to help test the mastery of basic knowledge. If you have carefully read or done them, I believe you should have a certain understanding of your mastery of knowledge. Next, you can relearn the part that is not very clear.
python basic syntax is OK? Do some tests
python basic syntax is OK? Do some tests (2)
python solution is OK? Do some tests (3)
Among the above three articles, the first and second articles are relatively simple. The content of the third article is indeed difficult if you have not specially studied the content related to data structure and algorithm. This is the opposite. Let's put the reference answers of the most difficult article first, and put the first and second articles in the next issue.
If you haven't read the third article, I suggest you think about it yourself first and try it according to your existing knowledge. Efficient learning or learning effect learning must produce a lot of effective thinking per unit time - that is, you have tried hard and tried various methods, but these thoughts are very helpful. You know your puzzles and problems to be solved; When you see the reference answer, it is completely different from those who have not thought. When these contents are successfully solved, your brain should make subtle changes in the game and make breakthroughs in technology.
Now officially enter the topic.
In order to make you better understand the following contents, let's talk about some larger concepts first.
Cycle of violence (exhaustive): most computer problems can be solved by exhaustive without considering time.
For example, we can find out all the schemes through exhaustive methods, and then find the one with the least quantity.

The same is true for Sudoku. There are four possibilities for each position. You can list all methods, and then judge the coincidence.

Similarly, the maze problem is the same.
The cycle of violence mentioned above is simple, but there are also some problems to face:
- How to ensure that all the information can be listed without omission?
- For example, how many non repeated 3 digits can be combined from 3, 4, 5, 6 and 4 numbers?
- 24 point game, random four numbers, 1, 3, 6, 9, plus, minus, multiplication and division (+ - * /), parentheses, how many situations can be combined?
- How to judge whether the current situation is inconsistent? Different problems lead to different difficulties. It's easy to judge the change. Maze and Sudoku are a little more troublesome.
- There is a large amount of data. It has been a long time without results. How can we speed up some speed?
- ......
To solve some of the above problems, we need to have some strategies, such as how to ensure that the poor cite all the cases, and the permutation and combination in mathematics is very popular.
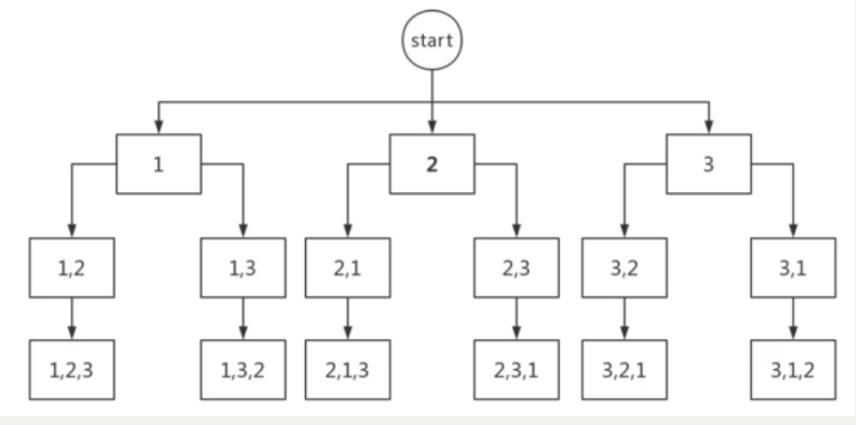
There are many ways to realize permutation and combination. For example, I have used multiple loops before, and of course I can also use recursion.
Full Permutation and combination implementation method
This method ensures that there is no leakage. The tree structure and many decision trees are similar.
Question 2 specific analysis.
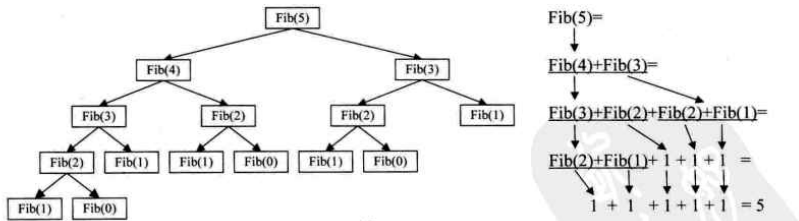
Problem 3: to reduce the data scale is to use recursion to calculate Fibonacci series. After 40 items are calculated, it is not increased once. The time is double. The computer card is stuck for a long time. The reason is repeated calculation. You can save the calculated values through a list and reduce repeated calculation, which will significantly improve the speed.
For example, if you find the target number in a range and judge it one by one from beginning to end, it must be slow. Two point search can cut half at a time. How large the range is, it becomes smaller after several times.
1. Find the smallest tuple value in the following list, and the maximum value is the same.
[(0, 1, 2), (3, 4, 5), (6, 7, 8), (9, 10, 11), (12, 13, 14), (15, 16, 17), (18, 19, 20), (21, 22, 23), (24, 25, 26)]
result:
Minimum:(0, 1, 2) Maximum:(24, 25, 26)
2. Find the most frequent element in the following list and print the number.
l = [1,3,4,5,6,1,3,4,5,1,9,1,1,1]
result:
1 Up to 6 times.
Reference for questions 1 and 2: python mosaic pixel map , which gives the solution.
3. Change problem
Given the types of change that can be found and the total amount of change to be found, find the scheme of the least amount of change.
For example, change 6 yuan,
Scheme 1: 4 1;
Scheme 2: 3,3;
Scheme 3: 3,1,1,1;
Scheme 4: 1,1,1,1,1,1;
Obviously, scheme 2 has the least number, only 2.
values = [1, 3, 4] # Coin face value total = 6 # I need change
result:
[3,3]
Refer to answer 1 - local optimal solution:
# Target number of change
total = 6
# Types of banknotes
values = [4, 3, 1]
# result
number = [0,0,0]
# Cycle, starting from the maximum face value
for i in range(3):
# Rounding to calculate the maximum number of sheets that can be found for the current face value
number[i] = total // values[i]
# Take the balance and calculate the amount of money left after the change of the current face value
total = total % values[i]
for i in range(3):
print(values[i],'The number of sheets of yuan is:',number[i],'Zhang')
Reference answer 2 - global optimal solution (dynamic programming):
I'm too lazy to write. I found a number on the Internet and changed it. I feel it's still very clear
def rec_mc(coin_value_list, change, know_results):
min_coins = change
if change in coin_value_list:
know_results[change] = 1
return 1
elif know_results[change] > 0:
return know_results[change]
else:
for i in [c for c in coin_value_list if c <= change]:
num_coins = 1 + rec_mc(coin_value_list, change-i, know_results)
if num_coins < min_coins:
min_coins = num_coins
know_results[change] = min_coins
return min_coins
print("===========Recursive implementation========================")
print(rec_mc([1, 3, 4], 6, [0]*7))
def dp_make_change(coin_value_list, change, min_coins, coins_used):
for cents in range(change+1):
coin_count = cents
new_coin = 1
for j in [c for c in coin_value_list if c <= cents]:
if min_coins[cents-j] + 1 < coin_count:
coin_count = min_coins[cents-j]+1
new_coin = j
min_coins[cents] = coin_count
coins_used[cents] = new_coin
return min_coins[change]
def print_coins(coins_used, change):
coin = change
while coin > 0:
this_coin = coins_used[coin]
print(this_coin)
coin = coin - this_coin
a_mnt = 6
c_list = [1, 3, 4]
c_used = [0] * (a_mnt+1)
c_count = [0] * (a_mnt+1)
print("===========Dynamic programming implementation========================")
print('Making change for ', a_mnt, 'requires')
print(dp_make_change(c_list, a_mnt, c_count, c_used), 'coins')
print("They are: ")
print_coins(c_used, a_mnt)
print("The used list is as follows: ")
print(c_used)4. Sudoku 4
Using the program to automatically complete 4 * 4 Sudoku
[[0, 1, 0, 0], [0, 0, 0, 2], [3, 0, 0, 0], [0, 0, 4, 0]]
result:

answer:
# Print board
def print_board(board):
for row in board:
print(row)
def check_board(num,row,col):
# Check the row and judge each grid of the row
for i in range(cols):
# If the number to be filled already exists
if board[row][i] == num:
return False
# Check the column and judge each grid of the column
for i in range(rows):
# If the number to be filled already exists
if board[i][col] == num:
return False
return True
def backtrack(board, index):
if index >= 16:
print("----programme----")
print_board(board)
print("------------")
else:
for num in range(1, len(board)+1):
row = index//len(board)
col = index%len(board[0])
if board[row][col]==0:
# Judge whether this number can be filled in
if not check_board(num, row, col):
continue
# Select a number
board[row][col] = num
backtrack(board,index+1)
# Number of unselected
board[row][col] = 0
else:
index = index +1
rows = 4
cols = 4
board = [[0 for i in range(rows)] for j in range(cols)]
board[0][1] = 1
board[1][3] = 2
board[2][0] = 3
board[3][2] = 4
index = 0
backtrack(board,index)Unpackaged visual Sudoku version:
from PIL import Image, ImageDraw
import matplotlib.pyplot as plt
#Title Setting Chinese
plt.rc("font", family='MicroSoft YaHei', weight='bold')
plt.ion()
# Print board
def print_board(board):
for row in board:
print(row)
def show_board(board, x, y, num):
img = Image.new("RGB", (100, 100), "white")
draw = ImageDraw.Draw(img)
for row in range(4):
for col in range(4):
pos = (0+30*col, 0+row*30)
draw.text(pos, str(board[row][col]), fill=(0, 0, 255))
draw.text((0+30*y, 0+x*30), str(num), fill=(255, 0, 255))
return img
def check_board(num, row, col):
# Check the row and judge each grid of the row
for i in range(cols):
# If the number to be filled already exists
if board[row][i] == num:
return False
# Check the column and judge each grid of the column
for i in range(rows):
# If the number to be filled already exists
if board[i][col] == num:
return False
return True
def backtrack(board, index):
if index >= 16:
print("----programme----")
print_board(board)
print("------------")
img = show_board(board, 3, 3, board[3][3])
plt.title("Compliant scheme") # title
plt.imshow(img)
plt.pause(5) # Pause for 1 second
else:
for num in range(1, 4+1):
row = index//4
col = index % 4
if board[row][col] == 0:
# Judge whether this number can be filled in
if not check_board(num, row, col):
continue
# Select a number
board[row][col] = num
plt.cla() # Clear the screen first
img = show_board(board, row, col, num)
plt.title("Fill in a number") # title
plt.imshow(img)
plt.pause(1) # Pause for 1 second
backtrack(board, index+1)
# Number of unselected
board[row][col] = 0
plt.cla() # Clear the screen first
img = show_board(board, row, col, num)
plt.title("Cancel a number") # title
plt.imshow(img)
plt.pause(1) # Pause for 1 second
else:
index = index + 1
rows = 4
cols = 4
board = [[0 for i in range(rows)] for j in range(cols)]
board[0][1] = 1
board[1][3] = 2
board[2][0] = 3
board[3][2] = 4
# plt.pause(5)
img = show_board(board, 3, 3, board[3][3])
plt.title("4X4 Sudoku game") # title
plt.imshow(img)
plt.pause(5)
plt.title("start")
plt.pause(2)
index = 0
backtrack(board, index)
plt.pause(2) # Pause for 1 second
plt.ioff()
plt.show()5. Sudoku 9
Increase the difficulty and use the program to automatically complete 9 * 9 Sudoku.
[[2, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 3, 6, 0, 0, 0, 0, 0], [0, 7, 0, 0, 9, 0, 2, 0, 0], [0, 5, 0, 0, 0, 7, 0, 0, 0], [0, 0, 0, 0, 4, 5, 7, 0, 0], [0, 0, 0, 1, 0, 0, 0, 3, 0], [0, 0, 1, 0, 0, 0, 0, 6, 8], [0, 0, 8, 5, 0, 0, 0, 1, 0], [0, 9, 0, 0, 0, 0, 4, 0, 0]]
Results: there are many answers, and only some are listed below.

answer:
# Print board
def print_board(board):
for row in board:
print(row)
def check_board(num,row,col):
# Check whether there are duplicate numbers in the row and column
for i in range(9):
if board[row][i] == num or board[i][col] == num:
return False
# Judge whether there is repetition in xiaojiugong
sub_row = row // 3
sub_col = col // 3
for i in range(3):
for j in range(3):
if board[sub_row * 3 + i][sub_col * 3 + j] == num:
return False
return True
def backtrack(board, index):
# print(index)
if index >= 81:
print("-----------programme-----------")
print_board(board)
print("--------------------------")
else:
for num in range(1, 9+1):
row = index//9
col = index%9
if board[row][col]==0:
# Judge whether this number can be filled in
if not check_board(num, row, col):
continue
# Select a number
board[row][col] = num
# Continue to select the next number
backtrack(board,index+1)
# Number of unselected
board[row][col] = 0
else:
# backtrack(board,index+1)
index = index + 1
board = [[2, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 3, 6, 0, 0, 0, 0, 0],
[0, 7, 0, 0, 9, 0, 2, 0, 0],
[0, 5, 0, 0, 0, 7, 0, 0, 0],
[0, 0, 0, 0, 4, 5, 7, 0, 0],
[0, 0, 0, 1, 0, 0, 0, 3, 0],
[0, 0, 1, 0, 0, 0, 0, 6, 8],
[0, 0, 8, 5, 0, 0, 0, 1, 0],
[0, 9, 0, 0, 0, 0, 4, 0, 0]]
index = 0
backtrack(board,index)Unpackaged visual Sudoku version:
from PIL import Image,ImageDraw
import matplotlib.pyplot as plt
#Title Setting Chinese
plt.rc("font", family='MicroSoft YaHei', weight='bold')
plt.ion()
# Print board
def print_board(board):
for row in board:
print(row)
def show_board(board,x,y,num):
img = Image.new("RGB", (250, 250), "white")
draw = ImageDraw.Draw(img)
for row in range(9):
for col in range(9):
pos = (0+30*col, 0+row*30)
draw.text(pos, str(board[row][col]), fill=(0, 0, 255))
draw.text((0+30*y, 0+x*30), str(num), fill=(255, 0, 255))
return img
def check_board(num, row, col):
# Check whether there are duplicate numbers in the row and column
for i in range(9):
if board[row][i] == num or board[i][col] == num:
return False
# Judge whether there is repetition in xiaojiugong
sub_row = row // 3
sub_col = col // 3
for i in range(3):
for j in range(3):
if board[sub_row * 3 + i][sub_col * 3 + j] == num:
return False
return True
def backtrack(board, index):
global count
# print(index)
if index >= 81:
count = count + 1
img = show_board(board, 8, 8, board[8][8])
plt.title("The first{}Suspension of 1 eligible scheme s".format(count)) # title
plt.imshow(img)
plt.pause(1) # Pause for 1 second
plt.title("Next plan") # title
plt.pause(1) # Pause for 1 second
print("-----------------------")
print_board(board)
else:
for num in range(1, 9+1):
row = index//9
col = index % 9
if board[row][col] == 0:
# Judge whether this number can be filled in
if not check_board(num, row, col):
continue
# Select a number
board[row][col] = num
plt.cla() # Clear the screen first
img = show_board(board,row,col,num)
plt.title("Fill in a number") # title
plt.imshow(img)
plt.pause(0.1) # Pause for 1 second
# Continue to select the next number
backtrack(board, index+1)
# Number of unselected
board[row][col] = 0
plt.cla() # Clear the screen first
img = show_board(board,row,col,num)
plt.title("Cancel a number") # title
plt.imshow(img)
plt.pause(0.1) # Pause for 1 second
else:
# backtrack(board,index+1)
index = index + 1
plt.cla() # Clear the screen first
board = [[2, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 3, 6, 0, 0, 0, 0, 0],
[0, 7, 0, 0, 9, 0, 2, 0, 0],
[0, 5, 0, 0, 0, 7, 0, 0, 0],
[0, 0, 0, 0, 4, 5, 7, 0, 0],
[0, 0, 0, 1, 0, 0, 0, 3, 0],
[0, 0, 1, 0, 0, 0, 0, 6, 8],
[0, 0, 8, 5, 0, 0, 0, 1, 0],
[0, 9, 0, 0, 0, 0, 4, 0, 0]]
img = show_board(board, 8, 8, board[8][8])
plt.title("9X9 Sudoku game") # title
plt.imshow(img)
plt.pause(2)
plt.title("start")
plt.pause(2)
index = 0
global count
count = 0
backtrack(board, index)
# plt.ioff()
plt.show()6. Maze problem
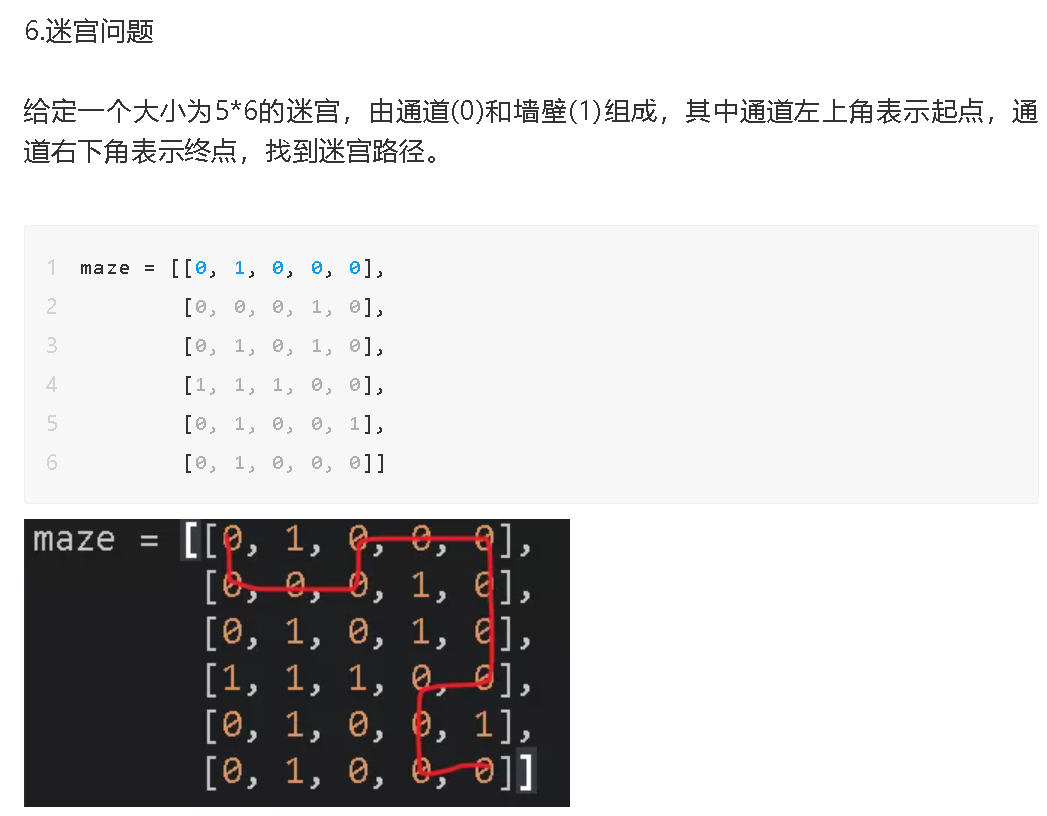
A maze with a size of 5 * 6 is given, which is composed of channel (0) and wall (1), in which the upper left corner of the channel represents the starting point and the lower right corner of the channel represents the end point. Find the maze path.
maze = [[0, 1, 0, 0, 0],
[0, 0, 0, 1, 0],
[0, 1, 0, 1, 0],
[1, 1, 1, 0, 0],
[0, 1, 0, 0, 1],
[0, 1, 0, 0, 0]]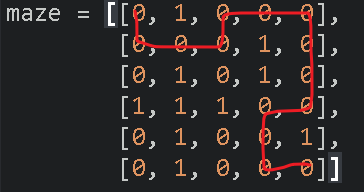
result:
[[0, 0], [1, 0], [1, 1], [1, 2], [0, 2], [0, 3], [0, 4], [1, 4], [2, 4], [3, 4], [3, 3], [4, 3], [5, 3], [5, 4]]
Answer 1:
# Shortest distance shortest path
maze =[[0, 1, 0, 0, 0],
[0, 1, 0, 1, 0],
[0, 0, 0, 0, 0],
[0, 1, 1, 1, 0],
[0, 0, 0, 1, 0]]
n,m = len(maze),len(maze[0])
start = [0, 0]
end = [4, 4]
# List of data to be found
search_queue = [] # List simulation queue
# Add start point
search_queue.append(start)
visted = [] # Record visited points
visted.append(start)
def find_next_point(point):
global search_queue,visted,n,m
# px and py arrays are used to realize the moving order of bottom left and top right
px = [-1, 0, 1, 0]
py = [0, -1, 0, 1]
# Move up, down, left and right
for i in range(4):
next_x = point[0] + px[i]
next_y = point[1] + py[i]
# How to add the next point to the queue to be searched and the access queue to meet the requirements
if (0 <= next_x < n and 0 <= next_y < m and maze[next_x][next_y] == 0 and [next_x,next_y] not in visted):
search_queue.append([next_x,next_y])
visted.append([next_x,next_y])
return True
return False
def dfs():
global search_queue,visted
print(search_queue)
while search_queue[-1] != end:
# Get the last point of the queue and judge whether to reach the big end point
point = search_queue[-1]
# If there is a next point, continue
if find_next_point(point):
continue
# Otherwise, delete the point you just added
else:
print("delete",search_queue.pop())
print(search_queue)
dfs()Answer 2:
The above is difficult to understand. You can see the following. I found a simple change on the Internet. It is easier to understand, but there are many codes
def up(point):
# You have reached the top of the array. You can't go up
if point[0] == 0:
return False
else:
new_point = [point[0] - 1, point[1]]
# The road we have traveled is no longer gone
if new_point in visted:
return False
# Don't go against the wall
elif maze[new_point[0]][new_point[1]] == 1:
return False
else:
search_queue.append(new_point)
visted.append(new_point)
return True
def down(point):
# When you meet the bottom of the maze, you can't go further
if point[0] == len(maze) - 1: # The number of two-dimensional array rows with 6 rows and 5 columns is calculated from 0, so it is 6-1 = 5 rows
return False
else:
new_point = [point[0] + 1, point[1]]
# The road we have traveled is no longer gone
if new_point in visted:
return False
# Don't go against the wall
elif maze[new_point[0]][new_point[1]] == 1:
return False
else:
visted.append(new_point)
search_queue.append(new_point)
return True
def left(point):
# You can't continue to go left when you meet the leftmost part of the maze
if point[1] == 0:
return False
else:
new_point = [point[0], point[1] - 1]
# The road we have traveled is no longer gone
if new_point in visted:
return False
# Don't go against the wall
elif maze[new_point[0]][new_point[1]] == 1:
return False
else:
visted.append(new_point)
search_queue.append(new_point)
return True
def right(point):
# You cannot continue to move to the right when you encounter the rightmost side of the maze
if point[1] == len(maze[0]) - 1: # The number of two-dimensional array columns with 6 rows and 5 columns is calculated from 0, so it is 5-1 = 4 rows
return False
else:
new_point = [point[0], point[1] + 1]
# The road we have traveled is no longer gone
if new_point in visted:
return False
# Don't go against the wall
elif maze[new_point[0]][new_point[1]] == 1:
return False
else:
visted.append(new_point)
search_queue.append(new_point)
return True
maze = [[0, 1, 0, 0, 0],
[0, 0, 0, 1, 0],
[0, 1, 0, 1, 0],
[1, 1, 1, 0, 0],
[0, 1, 0, 0, 1],
[0, 1, 0, 0, 0]]
start = [0, 0]
end = [5, 4]
search_queue = []
visted = []
search_queue.append(start)
visted.append(start)
print("start: %s --> end: %s\n" % (start, end))
while search_queue[-1] != end:
now = search_queue[-1]
if up(now) or down(now) or left(now) or right(now):
continue
print("delete",search_queue.pop())
print("final path: ", search_queue)7. Maze problem 2 - shortest path.
Given a maze with a size of 5 * 5, it is composed of channel (0) and wall (1), in which the upper left corner of the channel represents the starting point and the lower right corner of the channel represents the end point, so as to find the shortest path of the maze.
maze = [[0, 1, 0, 0, 0,],
[0, 1, 0, 1, 0,],
[0, 0, 0, 0, 0,],
[0, 1, 1, 1, 0,],
[0, 0, 0, 1, 0,]]There are two schemes, but scheme 2 is the shortest path.

answer:
# Shortest distance shortest path
maze =[[0, 1, 0, 0, 0],
[0, 1, 0, 1, 0],
[0, 0, 0, 0, 0],
[0, 1, 1, 1, 0],
[0, 0, 0, 1, 0]]
n,m = len(maze),len(maze[0])
start = [0, 0]
end = [4, 4]
# Define the Breadth First Search algorithm
def bfs(maze,n,m):
# List of data to be found
search_queue = [] # List simulation queue
# Add start point
search_queue.append(start)
visted = [] # Record visited points
visted.append(start)
# Record parent node
parent = {f"{start[0]}{start[1]}":None}
px = [-1, 0, 1, 0] # px and py arrays are used to realize the moving order of bottom left and top right
py = [0, -1, 0, 1]
# Exit the loop until the lookup queue is empty
while search_queue:
# Take out the first point in the queue (search started recently)
point = search_queue.pop(0)
# Get all nearest points
points = []
for i in range(4):
next_x = point[0] + px[i]
next_y = point[1] + py[i]
if (0 <= next_x < n and 0 <= next_y < m and maze[next_x][next_y] == 0):
points.append([next_x,next_y])
for i in points:
# If i have not been visited
if i not in visted:
# Add I (nearest point) to the search queue
search_queue.append(i)
# Mark i as accessed
visted.append(i)
# Record the parent node of each point
parent[f"{i[0]}{i[1]}"] = point
return visted,parent
visted,parent = bfs(maze,n,m)
route_list = []
if end in visted:
print(f"Existence from{start}reach{ end}Route")
v = end # Currently accessed point
# Until the start position None exits
while v !=None:
route_list.append(v)
v=parent[f"{v[0]}{v[1]}"]
else:
print(f"Does not exist from{start}reach{ end}Route")
route_list.reverse()
print(route_list)How to see the above methods is difficult. You can look at the concepts of DFS and BFS, backtracking, recursion and so on. You can also take a look at what I wrote before. I have time to update it later. What I wrote before is not very good. I can make do with it.
Full Permutation and combination implementation method
Thoughts on learning algorithms (end of full text)