introduction

These two questions are mainly to investigate the mastery of binary tree traversal, that is, the original binary tree is derived from the front order and middle order, and the original binary tree is derived from the back order and middle order. Let's talk about the derivation process first;
Preorder and middle order
Know the preorder traversal and inorder traversal, how to push the original binary tree? (it is a direct conclusion, which can be deduced by yourself)
1. First look at the first element in the preamble. This element value is the element value of the root node
2. Find the element first from the middle order traversal. All elements on the left of the element are the nodes on the left subtree of the binary tree, and all elements on the right are the nodes on the right subtree of the binary tree. That is, the middle order traversal result is divided into two parts
3. Just look at the left side of the middle order traversal. All elements on the left side who are in front of the first order traversal are the root node of the left tree, which is the same as the right tree (in fact, it is similar to repeating the first two steps, a recursive process), and so on;

Post order and middle order
1. First look at the last element of the last order. This element value is the element value of the root node
2. Find the element last from the middle order traversal. All elements on the left of the element are the nodes on the left subtree of the binary tree, and all elements on the right are the nodes on the right subtree of the binary tree. That is, the middle order traversal result is divided into two parts
3. Repeat the first two steps until the end

It can be found that the difference between the pre order and the post order is that the pre order starts from the front and the post order starts from the back;

So can we deduce the original binary tree until preorder traversal and postorder traversal?
No, I don't believe I can try;

This is the process of pushing the original binary tree by knowing the traversal order. If you don't understand it, it is recommended to study it carefully in the traversal chapter of the binary tree of the data structure and try a few more examples;

With this foundation, let's talk about these two questions;

Constructing binary tree from preorder and inorder traversal sequences

Given the preorder and inorder of a tree. Construct a binary tree and return its root node.

Example 1:

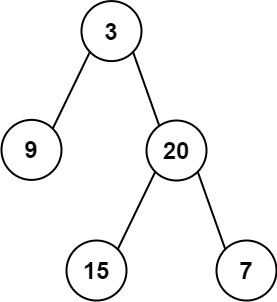
Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
Output: [3,9,20,null,null,15,7]

Example 2:
Input: preorder = [-1], inorder = [-1]
Output: [-1]

Tips:

1 <= preorder.length <= 3000
inorder.length == preorder.length
-3000 <= preorder[i], inorder[i] <= 3000
Neither preorder nor inorder has duplicate elements
Inorders appear in preorder
Preorder is guaranteed to be the preorder traversal sequence of binary tree
inorder is guaranteed to be a middle order traversal sequence of binary tree

We already know how to introduce the original binary tree. It may be difficult to implement it in code here. Let's solve it one by one;
1. I can definitely think of the need for recursion. We only need to find the first node traversed by the preamble, and then recursively generate the left subtree and the right subtree respectively;
2. The main point here is how to find the root node in the middle order traversal? This can use a hash table to quickly find the location of the root node and return the subscript;
Here you can go directly to the code, and the comments are clearer in the code

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int posFirst;
    unordered_map<int, int> hash;
    //The function is to construct a binary tree through the preorder and inorder traversal sequences
    TreeNode* helper(int posLeft, int posRight, vector<int>& preorder, vector<int>& inorder) {
        //When the left and right subtrees are empty, the recursion ends
        if (posLeft > posRight) 
            return NULL;

        //Find the val value of the root node and create the root node
        int rootVal = preorder[posFirst];
        TreeNode* root = new TreeNode(rootVal);

        //Find the subscript of the root node in the middle order traversal
        int index = hash[rootVal];

        //The coordinates of the previous traversal continue backward in order to find the root nodes of the left and right subtrees
        posFirst++;

        //To create a left subtree and a right subtree, you must first go from left to right, because posFirst goes through the root node of the left subtree first and then the root node of the right subtree
        root -> left = helper(posLeft, index - 1, preorder, inorder);
        root -> right = helper(index + 1, posRight, preorder, inorder);
        return root;
    }
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        posFirst = 0;
        int idx = 0;
        //Store the middle order traversal results in the hash table. The key value is val and the value value is subscript
        for (auto& val : inorder) {
            hash[val] = idx++;
        }
        return helper(posFirst, inorder.size() - 1, preorder, inorder);
    }
};

Constructing binary tree from middle order and post order traversal sequences

According to the middle order traversal and post order traversal of a tree, a binary tree is constructed.

be careful:
You can assume that there are no duplicate elements in the tree.

For example, give
Middle order traversal inorder = [9,3,15,20,7]
Postorder traversal postorder = [9,15,7,20,3]
Return the following binary tree:

The problem is as like as two peas. The only point to distinguish is the root node from the back, and the first to build the right sub tree and the left sub tree.
The code is as follows:

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int posLast;
    unordered_map<int, int> hash;
    //The function is to construct a binary tree through post order and middle order traversal
    TreeNode* helper(int posLeft, int posRight, vector<int>& inorder, vector<int>& postorder) {
        //When the left and right subtrees are empty, the recursion ends
        if (posLeft > posRight) 
            return NULL;

        //Find the val value of the root node and create the root node
        int rootVal = postorder[posLast];
        TreeNode* root = new TreeNode(rootVal);

        //Find the subscript of the root node in the middle order traversal
        int index = hash[rootVal];

        //The postorder traversal coordinates continue forward in order to find the root nodes of the left and right subtrees later
        posLast--;

        //To create a right subtree and a left subtree, you must first go right and then left, because postlast goes through the root node of the right subtree and then the root node of the left subtree
        root -> right = helper(index + 1, posRight, inorder, postorder);
        root -> left = helper(posLeft, index - 1, inorder, postorder);
        return root;
    }
    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
        posLast = (int)postorder.size() - 1;
        int idx = 0;
        //Store the middle order traversal results in the hash table. The key value is val and the value value is subscript
        for (auto& val : inorder) {
            hash[val] = idx++;
        }
        return helper(0, posLast, inorder, postorder);
    }
};

summary

These two questions are very classic binary tree traversal questions. The idea is relatively simple, but the code implementation may be a little difficult. Therefore, we must be familiar with the three basic traversals of binary tree and be able to flexibly use hash table to help the process implementation;