1. Title

Given two nonnegative integers num1 and num2 in string form, return the product of num1 and num2, and their product is also expressed in string form.

Example 1:

input: num1 = "2", num2 = "3"
output: "6"

Example 2:

input: num1 = "123", num2 = "456"
output: "56088"

explain:

1. The length of num1 and num2 is less than 110.
2. num1 and num2 contain only the numbers 0-9.
3. num1 and num2 do not start with zero unless it is the number 0 itself.
4. You cannot use the large number type of any standard library (such as BigInteger) or directly convert the input to an integer.

2. Train of thought

(string emulation) O ( n ∗ m ) O(n*m) O(n∗m)

Ordinary vertical

Take num1 = 123, num2 = 456 as an example: we traverse each bit of num2, multiply with num1, and accumulate the results of each step. In this process, if the result of multiplication or addition is greater than or equal to 10, we have to go to full 10 carry, as shown in the figure below:

In this way, the method of simulating ordinary vertical calculation is more complex, and we can consider the optimized version of vertical calculation.

Optimized vertical

In fact, in each bit of the multiplication or addition calculation process, we can consider not to fill the 10 carry first. After calculating all the multiplication results, we can finally add them to one piece, and then fill the 10 carry. The final result is the same as the ordinary vertical form, but it can greatly simplify our simulation process. (as shown in the figure below)

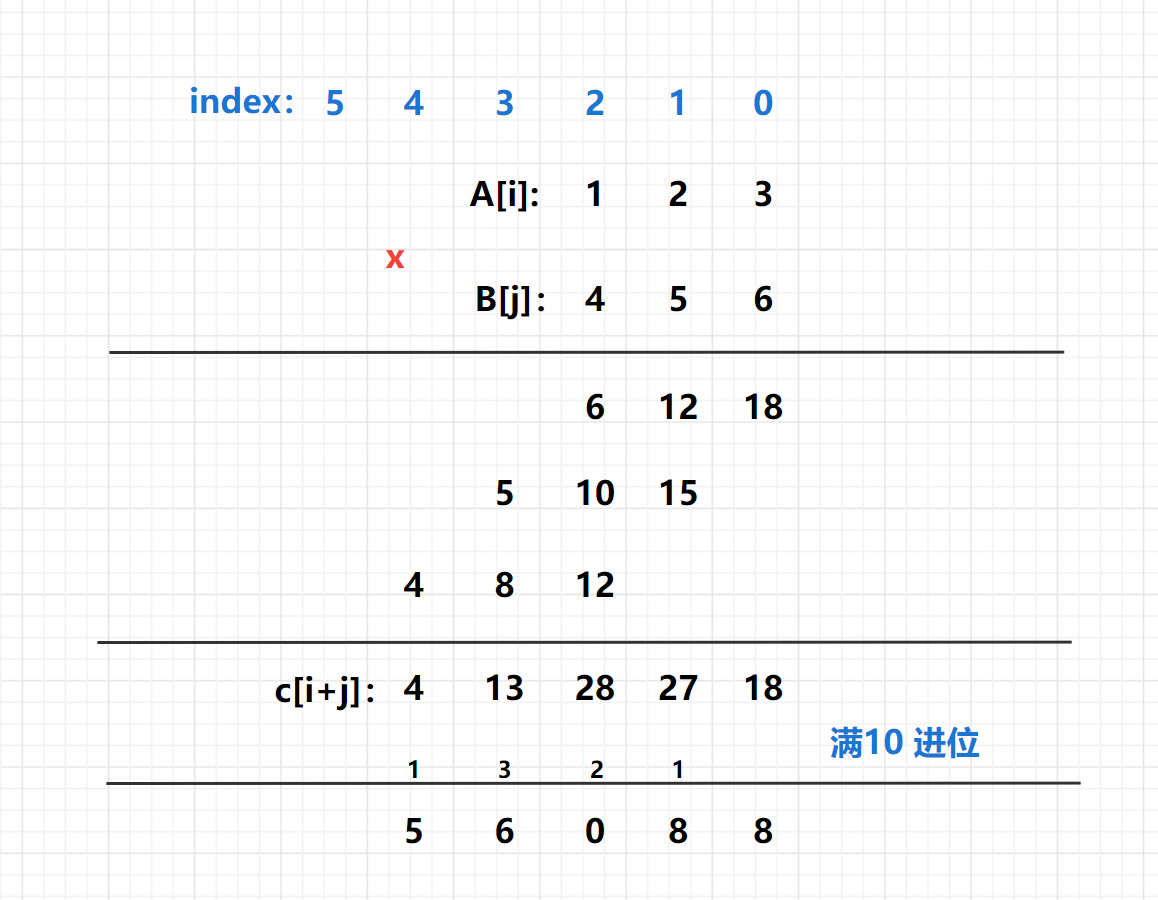
The specific process is as follows:

• 1. Multiply the numbers with length N and length m, and there are only N + m bits at most. In order to facilitate calculation, num1 and num2 are inversely stored in A [] and B [], that is, the low bits are in front of the array, and A C [] with size n + m is opened to store the calculated answer.
• 2. When the two numbers are multiplied, the result of A[i] * B[j] is accumulated into C[i + j]. Finally, C[i + j] indicates that the value of the digit i + j is C[i + j] (as shown in the above figure)
• 3. Since some bit numbers in the C [] array may be greater than or equal to 10, we enumerate from 0 to n + m - 1, carry out full 10 carry, and change the values of all bits into single digits.
• 4. Finally, the C [] array is inverted and output.

Details:

• The high order of the resulting array C [] may contain leading 0, so the high-order leading 0 must be removed before inversion.

Time complexity analysis: O ( n ∗ m ) O(n*m) O(n∗m)， n n n and m m m are n u m 1 num1 num1 and n u m 2 num2 Length of num2.

3. c + + code

class Solution {
public:
    string multiply(string num1, string num2) {
        vector<int> A, B;
        int n = num1.size(), m = num2.size();
        for (int i = n - 1; i >= 0; i -- ) A.push_back(num1[i] - '0'); //Reverse storage
        for (int i = m - 1; i >= 0; i -- ) B.push_back(num2[i] - '0');
        vector<int> C(n + m);
        for (int i = 0; i < n; i ++ )
            for (int j = 0; j < m; j ++ )
                C[i + j] += A[i] * B[j];
        int t = 0;  //Store carry
        for (int i = 0; i < C.size(); i ++ ) {
            t += C[i];
            C[i] = t % 10;
            t /= 10;
        }
        int k = C.size() - 1;
        while (k > 0 && !C[k]) k -- ;  //Remove leading 0
        string res;
        while (k >= 0) res += C[k -- ] + '0';  //reversal
        return res;
    }
};

4. java code

class Solution {
    public String multiply(String num1, String num2) {

        int n = num1.length(), m = num2.length();
        int[] A = new int[n], B = new int[m];
        for (int i = n - 1; i >= 0; i--) A[n - 1 - i] = num1.charAt(i) - '0';
        for (int i = m - 1; i >= 0; i--) B[m - 1 - i] = num2.charAt(i) - '0';

        int[] C = new int[n + m];
        for (int i = 0; i < n; i++)
            for (int j = 0; j < m; j++)
                C[i + j] += A[i] * B[j];
        int t = 0;
        for (int i = 0; i < C.length; i++) {
            t += C[i];
            C[i] = t % 10;
            t /= 10;
        }
        int k = C.length - 1;
        while (k > 0 && C[k] == 0) k--;
        StringBuilder sb = new StringBuilder();
        while (k >= 0) sb.append((char)(C[k--] + '0'));
        return sb.toString();
    }
}

Original title link: 43. String multiplication