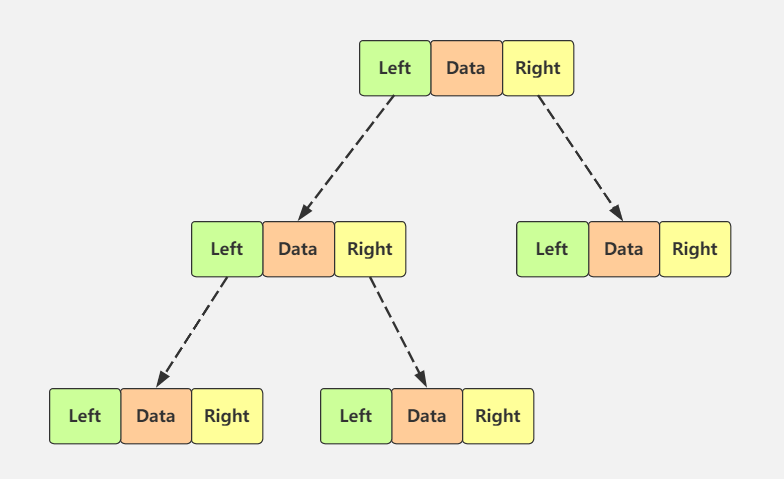
Binary tree refers to an ordered tree in which the degree of nodes in the tree is no more than 2. It is the simplest and most important tree. The recursive definition of binary tree is: a binary tree is an empty tree, or a non empty tree composed of a root node and two disjoint left and right subtrees called roots respectively; the left and right subtrees are also binary trees
Related terms:
-
Node: contains a data element and several information pointing to the branches of the subtree
-
Node degree: the number of subtrees a node has is called node degree
-
Leaf node: also known as terminal node, node without subtree or node with zero degree
-
Branch node: also known as non terminal node. Nodes with degree not zero are called non terminal nodes
-
Degree of tree: the maximum degree of all nodes in the tree
-
Node hierarchy: starting from the root node, it is assumed that the root node is layer 1 and the child nodes of the root node are layer 2, and so on. If a node is located in layer L, its child nodes are located in layer L + 1
-
Tree depth: also known as the height of the tree. The maximum hierarchical value of all nodes in the tree is called the depth of the tree
-
Ordered tree: if the order of each tree in the tree is in order, the tree is called ordered tree
-
Unordered tree: if the order of each tree in the tree has no order, the tree is called unordered tree
10. Forest: a forest is composed of m (m ≥ 0) disjoint trees. If the root node of a non empty tree is deleted, the tree becomes a forest, and the tree in the forest is composed of all the sub trees of the original root node
Special type:
-
Full binary tree: refers to a binary tree with a depth of K and 2^k - 1 nodes
-
Complete binary tree: set the depth of the binary tree as h, the number of nodes in other layers reaches the maximum except layer h, and all nodes in layer h are continuously concentrated on the far left. In other words, the n nodes contained in the tree correspond to the nodes numbered 1 to n in the full binary tree one by one
-
The left child node of the nth element is 2n
-
The right child node of the nth element is 2n + 1
-
The parent node of the nth element is (n - 1) / 2
-
nature:
-
There are at most 2^(i - 1) points (i ≥ 1) on layer i of binary tree
-
A binary tree with depth h contains at most 2^h - 1 nodes
-
If there are n0 leaf nodes and n2 nodes with degree 2 in any binary tree, there must be n0 = n2 + 1
-
The depth of a complete binary tree with n nodes is log2(x + 1), where X represents the largest integer not greater than n
-
If a complete binary tree with n nodes is sequentially numbered (1 ≤ i ≤ n), then for the node numbered i (i ≥ 1):
When i = 1, the node is the root and it has no parents
When I > 1, the number of the parent node of the node is i / 2
If 2i < n, there is a left node numbered 2i, otherwise there is no left node
If 2i + 1 ≤ n, there is a right node numbered 2i + 1, otherwise there is no right node
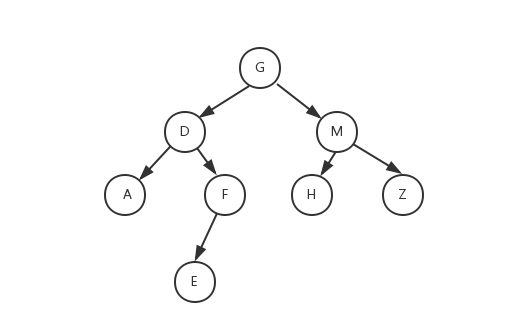
Preorder traversal binary tree
Idea:
After accessing a node, print the node and continue to traverse its left and right subtrees
Traversal order:
GDAFEMHZ
Code implementation:
//Preorder traversal
public void preOrder(){
//Print parent node
System.out.println(this);
//Recursive pre order traversal to the left subtree
if (this.left != null){
this.left.preOrder();
}
//Recursive right subtree preorder traversal
if (this.right != null){
this.right.preOrder();
}
}
Middle order traversal binary tree

Idea:
After accessing a node, temporarily store it. After traversing the left subtree, print the value of the node, and then traverse the right subtree
Traversal order:
ADEFGHMZ
Code implementation:
//Medium order traversal
public void infixOrder(){
//Recursive traversal to the middle order of the left subtree
if (this.left != null){
this.left.infixOrder();
}
//Print parent node
System.out.println(this);
//Recursive traversal in right subtree
if (this.right != null){
this.right.infixOrder();
}
}
Subsequent traversal of binary tree

Idea:
After accessing a node, temporarily store it. After traversing the left and right subtrees, print the value of the node
Traversal order:
AEFDHZMG
Code implementation:
//Postorder traversal
public void postOrder(){
//Recursive postorder traversal to the left subtree
if (this.left != null){
this.left.postOrder();
}
//Recursive postorder traversal of right subtree
if (this.right != null){
this.right.postOrder();
}
//Print parent node
System.out.println(this);
}
Hierarchical traversal binary tree

Idea:
Establish a circular queue. First put the root node of the binary tree into the queue, then out of the queue and access the root node. If it has a left subtree, put the root node of the left subtree in the queue; if it has a right subtree, put the root node of the right subtree in the queue. Then go out of the queue and access the out of queue node. Repeat until the queue is empty
Traversal order:
ADMAFHZ
Code implementation:
//level traversal
public void levelOrder(){
ArrayDeque<HeroNode> queue = new ArrayDeque<>(20);
//First, add the root node to the queue
queue.add(this);
//Traversal binary tree
while(!queue.isEmpty()){
HeroNode tempNode = queue.poll();
System.out.println(tempNode);
if (tempNode.left != null){
queue.add(tempNode.left);
}
if (tempNode.right != null){
queue.add(tempNode.right);
}
}
}
Preorder search Binary Tree

Idea:
-
First, compare the root nodes. If they are equal, return directly. Otherwise, search in the left recursive preamble
-
If it is found by left recursion, it returns directly; otherwise, it is found by right recursion
-
If the right recursion finds the return, otherwise it returns null
Node H found
Number of comparisons:
7
Code implementation:
//Preorder traversal
public HeroNode preOrdersearch(int no){
System.out.println("Enter preorder traversal");
//Compare whether the current node is
if (this.no == no){
return this;
}
//1. Judge whether the left child node of the current node is empty. If not, recursive preorder search
//2. If the left recursive preorder search finds a node, it returns
HeroNode resNode = null;
if (this.left != null){
resNode = this.left.preOrdersearch(no);
}
if (resNode != null){ //That means we found the left subtree
return resNode;
}
//1. Left recursive preorder search. If a node is found, it returns. Continue to judge whether or not
//2. Whether the right child node of the current node is empty. If it is not empty, continue to search in the right recursive preamble
if (this.right != null){
resNode = this.right.preOrdersearch(no);
}
return resNode;
}
Middle order search Binary Tree

Idea:
-
First, left recursive search. If it is found, it returns directly. Otherwise, it is compared with the root node
-
If the comparison is equal, return directly, otherwise right recursive middle order search
-
Returns if the right recursion is found, otherwise returns null
Find H node
Number of comparisons:
6
Code implementation:
//Medium order traversal
public HeroNode infixOrderSearch(int no){
//Judge whether the left child node of the current node is empty. If it is not empty, search in recursive middle order
HeroNode resNode = null;
if(this.left != null){
resNode = this.left.infixOrderSearch(no);
}
if (resNode != null){
return resNode;
}
System.out.println("Enter middle order traversal");
//If found, it returns. If not found, it is compared with the current node. If yes, it returns the current node
if (this.no == no){
return this;
}
//Otherwise, continue the middle order search of right recursion
if (this.right != null){
resNode = this.right.infixOrderSearch(no);
}
return resNode;
}
Postorder search Binary Tree

Idea:
-
First, the left recursive search. If it is found, it returns directly. Otherwise, the right recursive middle order search
-
If the right recursion is found, it returns directly. Otherwise, it is compared with the root node
-
Returns NULL if the comparison is not equal
Find H node
Number of comparisons:
5
Code implementation:
//Postorder traversal
public HeroNode postOrderSearch(int no){
//Judge whether the left child node of the current node is empty. If it is not empty, it will be searched recursively
HeroNode resNode = null;
if (this.left != null){
resNode = this.left.postOrderSearch(no);
}
if (resNode != null){ //Description found in the left subtree
return resNode;
}
//If the left subtree is not found, the right subtree recursively performs a post order traversal search
if (this.right != null){
resNode = this.right.postOrderSearch(no);
}
if (resNode != null){
return resNode;
}
System.out.println("Enter post order traversal");
//If the left and right subtrees are not found, compare the current node
if (this.no == no){
return this;
}
return resNode;
}
4. Delete node from binary tree
Idea:
-
If the deleted node is the root node, it is equivalent to setting the binary tree empty
-
If the deleted node is a non leaf node, the subtree is deleted
-
If the deleted node is a leaf node, delete the node
-
Because our binary tree is unidirectional, we can only judge whether the child nodes of the current node need to be deleted
-
If the left child node of the current node is not empty and the left child node is the node to be deleted, execute this Left = null and return
-
If the right child node of the current node is not empty and the left child node is the node to be deleted, execute this Right = null and return
-
If there is no return in steps 1 and 2, we need to delete the left subtree recursively
-
If there is still no return in step 3, recursively delete the right subtree
5. Binary tree synthesis example
code:
package com.sisyphus.tree;
import java.util.ArrayDeque;
/**
* @Description: Binary tree$
* @Param: $
* @return: $
* @Author: Sisyphus
* @Date: 7/23$
*/
public class BinaryTreeDemo {
public static void main(String[] args) {
//First create a binary tree
BinaryTree binaryTree = new BinaryTree();
//Create required nodes
HeroNode root = new HeroNode(1, "Song Jiang");
HeroNode node2 = new HeroNode(2, "Wu Yong");
HeroNode node3 = new HeroNode(3, "Lu Junyi");
HeroNode node4 = new HeroNode(4, "Lin Chong");
HeroNode node5 = new HeroNode(5, "Guan Sheng");
//Note: we first create the binary tree manually, and then we learn to create the binary tree recursively
root.setLeft(node2);
root.setRight(node3);
node3.setRight(node4);
node3.setLeft(node5);
binaryTree.setRoot(root);
System.out.println("Preorder traversal"); //12354
binaryTree.preOrder();
System.out.println("Medium order traversal"); //21534
binaryTree.infixOrder();
System.out.println("Postorder traversal"); //25431
binaryTree.postOrder();
//Preorder traversal
System.out.println("Preorder traversal");
HeroNode resNode = binaryTree.preOrderSearch(5);
if (resNode != null){
System.out.printf("Yes, the information is no=%d name=%s",resNode.getNo(),resNode.getName());
System.out.println();
}else{
System.out.printf("Can't find no=%d Hero of",5);
System.out.println();
}
//Medium order traversal
System.out.println("Medium order traversal");
resNode = binaryTree.infixOrderSearch(5);
if (resNode != null){
System.out.printf("Yes, the information is no=%d name=%s",resNode.getNo(),resNode.getName());
System.out.println();
}else{
System.out.printf("Can't find no=%d Hero of",5);
System.out.println();
}
//Postorder traversal
System.out.println("Postorder traversal");
resNode = binaryTree.postOrderSearch(5);
if (resNode != null){
System.out.printf("Yes, the information is no=%d name=%s",resNode.getNo(),resNode.getName());
System.out.println();
}else{
System.out.printf("Can't find no=%d Hero of",5);
System.out.println();
}
System.out.println("===================================================");
//Test delete node
System.out.println("Pre sequence traversal before deletion");
binaryTree.preOrder();
binaryTree.delNode(5);
System.out.println("After deletion, the preamble traverses");
binaryTree.preOrder();
System.out.println("======================================================");
System.out.println("level traversal ");
binaryTree.levelOrder();
}
}
//Define BinaryTree
class BinaryTree{
private HeroNode root;
public void setRoot(HeroNode root){
this.root = root;
}
//Delete Vertex
public void delNode(int no){
if (root != null){
//If there is only one root node, judge whether root is the node to be deleted immediately
if (root.getNo() == no){
root = null;
}else{
//Recursive deletion
root.delNode(no);
}
}else{
System.out.println("The tree is empty and cannot be deleted");
}
}
//++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
//ergodic
//Preorder traversal
public void preOrder(){
if (this.root != null){
this.root.preOrder();
}else{
System.out.println("The current binary tree is empty and cannot be traversed");
}
}
//Medium order traversal
public void infixOrder(){
if (this.root != null){
this.root.infixOrder();
}else{
System.out.println("The current binary tree is empty and cannot be traversed");
}
}
//Postorder traversal
public void postOrder(){
if (this.root != null){
this.root.postOrder();
}else{
System.out.println("The current binary tree is empty and cannot be traversed");
}
}
//level traversal
public void levelOrder(){
if (this.root != null){
this.root.levelOrder();
}else{
System.out.println("The current binary tree is empty and cannot be traversed");
}
}
//++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
//lookup
//Preorder traversal
public HeroNode preOrderSearch(int no){
if (root != null){
return root.preOrdersearch(no);
}else{
return null;
}
}
//Medium order traversal
public HeroNode infixOrderSearch(int no){
if (root != null){
return root.infixOrderSearch(no);
}else{
return null;
}
}
//Postorder traversal
public HeroNode postOrderSearch(int no){
if (root != null){
return root.postOrderSearch(no);
}else{
return null;
}
}
}
//Create the HeroNode node first
class HeroNode{
private int no;
private String name;
private HeroNode left;
private HeroNode right;
public HeroNode(int no, String name) {
this.no = no;
this.name = name;
}
public int getNo() {
return no;
}
public void setNo(int no) {
this.no = no;
}
public String getName() {
return name;
}
public void setName(String name) {
this.name = name;
}
public HeroNode getLeft() {
return left;
}
public void setLeft(HeroNode left) {
this.left = left;
}
public HeroNode getRight() {
return right;
}
public void setRight(HeroNode right) {
this.right = right;
}
@Override
public String toString() {
return "HeroNode{" +
"no=" + no +
", name='" + name + '\'' +
'}';
}
//Recursively delete nodes
public void delNode(int no){
if (this.left != null && this.left.no == no){
this.left = null;
return;
}
if (this.right != null && this.right.no == no){
this.right = null;
return;
}
if (this.left != null){
this.left.delNode(no);
}
if (this.right != null){
this.right.delNode(no);
}
}
//+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
//ergodic
//Preorder traversal
public void preOrder(){
//Print parent node
System.out.println(this);
//Recursive pre order traversal to the left subtree
if (this.left != null){
this.left.preOrder();
}
//Recursive right subtree preorder traversal
if (this.right != null){
this.right.preOrder();
}
}
//Medium order traversal
public void infixOrder(){
//Recursive traversal to the middle order of the left subtree
if (this.left != null){
this.left.infixOrder();
}
//Print parent node
System.out.println(this);
//Recursive traversal in right subtree
if (this.right != null){
this.right.infixOrder();
}
}
//Postorder traversal
public void postOrder(){
//Recursive postorder traversal to the left subtree
if (this.left != null){
this.left.postOrder();
}
//Recursive postorder traversal of right subtree
if (this.right != null){
this.right.postOrder();
}
//Print parent node
System.out.println(this);
}
//level traversal
public void levelOrder(){
ArrayDeque<HeroNode> queue = new ArrayDeque<>(20);
//First, add the root node to the queue
queue.add(this);
//Traversal binary tree
while(!queue.isEmpty()){
HeroNode tempNode = queue.poll();
System.out.println(tempNode);
if (tempNode.left != null){
queue.add(tempNode.left);
}
if (tempNode.right != null){
queue.add(tempNode.right);
}
}
}
//++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
//lookup
//Preorder traversal
public HeroNode preOrdersearch(int no){
System.out.println("Enter preorder traversal");
//Compare whether the current node is
if (this.no == no){
return this;
}
//1. Judge whether the left child node of the current node is empty. If not, recursive preorder search
//2. If the left recursive preorder search finds a node, it returns
HeroNode resNode = null;
if (this.left != null){
resNode = this.left.preOrdersearch(no);
}
if (resNode != null){ //That means we found the left subtree
return resNode;
}
//1. Left recursive preorder search. If a node is found, it returns. Continue to judge whether or not
//2. Whether the right child node of the current node is empty. If it is not empty, continue to search in the right recursive preamble
if (this.right != null){
resNode = this.right.preOrdersearch(no);
}
return resNode;
}
//Medium order traversal
public HeroNode infixOrderSearch(int no){
//Judge whether the left child node of the current node is empty. If it is not empty, search in recursive middle order
HeroNode resNode = null;
if(this.left != null){
resNode = this.left.infixOrderSearch(no);
}
if (resNode != null){
return resNode;
}
System.out.println("Enter middle order traversal");
//If found, it returns. If not found, it is compared with the current node. If yes, it returns the current node
if (this.no == no){
return this;
}
//Otherwise, continue the middle order search of right recursion
if (this.right != null){
resNode = this.right.infixOrderSearch(no);
}
return resNode;
}
//Postorder traversal
public HeroNode postOrderSearch(int no){
//Judge whether the left child node of the current node is empty. If it is not empty, it will be searched recursively
HeroNode resNode = null;
if (this.left != null){
resNode = this.left.postOrderSearch(no);
}
if (resNode != null){ //Description found in the left subtree
return resNode;
}