1, Introduction to grey Wolf algorithm
1 Preface:
Grey Wolf Optimizer (GWO) is a population intelligent optimization algorithm proposed by Mirjalili, a scholar at Griffith University in Australia, in 2014. Inspired by the gray wolf's prey hunting activities, the algorithm is an optimization search method. It has the characteristics of strong convergence, few parameters and easy implementation. In recent years, it has been widely concerned by scholars. It has been successfully applied to the fields of job shop scheduling, parameter optimization, image classification and so on.
2. Algorithm principle:
Gray wolf belongs to the social canine family and is at the top of the food chain. Gray wolves strictly abide by a hierarchy of social dominance. As shown in the figure:
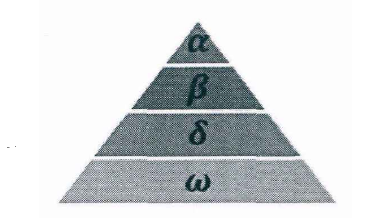
The first level of social hierarchy: the first wolf in the wolf pack is recorded as 
， Wolves are mainly responsible for making decisions on predation, habitat, work and rest time and other activities. Because other wolves need to obey Wolf orders, so Wolves are also called dominant wolves. In addition, Wolves are not necessarily the strongest wolves in the pack, but in terms of management ability, The wolf must be the best.
Social class level 2: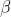
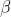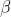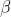Wolf, it obeys Wolf, and assist Wolves make decisions. stay When wolves die or grow old, The wolf will be The best candidate for the wolf. although Wolf obedience Wolf, but Wolves can dominate wolves at other social levels.
Social class level 3: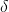
Wolf, it obeys , 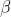Wolves, which dominate the remaining levels at the same time. 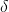Wolves are generally composed of young wolves, sentinel wolves, hunting wolves, old wolves and nursing wolves.
Social class level 4: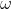
Wolf, it usually needs to obey wolves at other social levels. Although it seems 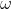Wolves don't play a big role in wolves, but if they don't 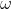With the existence of wolves, wolves will have internal problems, such as killing each other.
GWO optimization process includes the steps of gray wolf's social hierarchy, tracking, encircling and attacking prey. The specific steps are as follows.
1) Social Hierarchy when designing GWO, it is first necessary to build the gray wolf Social Hierarchy model. Calculate the fitness of each individual in the population, and mark the three gray wolves with the best fitness as , ,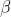 , 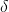and the remaining gray wolves are marked 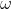. In other words, the social rank of gray wolf group is from high to low; , ,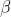 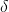and 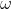. The optimization process of GWO is mainly composed of the best three solutions in each generation of population (i.e , ,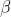 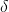)To guide the completion.
2) Encircling Prey the grey wolf will gradually approach the prey and encircle it. The mathematical model of this behavior is as follows:
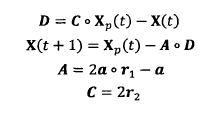
Where: t is the current number of iterations:. express hadamard product Operation; A and C are synergy coefficient vectors; Xp represents the position vector of prey; X(t) represents the position vector of the current gray wolf; In the whole iterative process, a decreases linearly from 2 to 0; r1 and r2 are random vectors in [0, 1].
3) Hunting
Gray wolf has the ability to identify the location of potential prey (optimal solution), and the search process mainly depends on , ,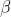 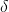With the guidance of the gray wolf. However, the solution space characteristics of many problems are unknown, and the gray wolf can not determine the exact location of prey (optimal solution). In order to simulate the search behavior of gray wolf (candidate solution), it is assumed that , ,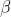 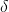It has strong ability to identify the location of potential prey. Therefore, during each iteration, the best three gray wolves in the current population are retained( , ,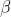 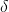)And then update other search agents (including 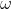)The location of the. The mathematical model of this behavior can be expressed as follows:
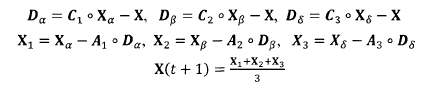
Where: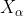
,
,
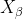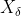Each represents the current population , ,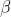 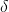Position vector of; X represents the position vector of gray wolf;
,
,
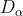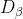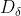Respectively represent the distance between the current candidate gray wolf and the best three wolves; When ｜ > 1, gray wolves disperse in various areas and search for prey as much as possible. When ｜ < 1, the gray wolf will concentrate on the prey in one or some areas.
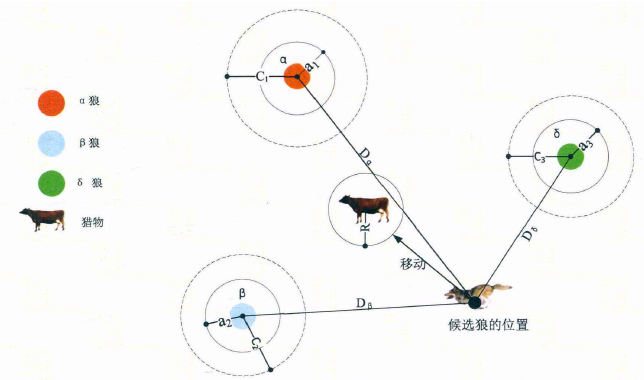
As can be seen from the figure, the position of the candidate solution finally falls on the target , , Defined random circle position. in general, , , 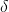First, the approximate location of the prey (potential optimal solution) needs to be predicted, and then other candidate wolves randomly update their location near the prey under the guidance of the current optimal Blue Wolf.
4) In the process of constructing the attack prey model, according to the formula in 2), the decrease of a value will cause the value of a to fluctuate. In other words, a is a random vector on the interval [- a,a] (Note: in the first paper of the original author, it is [- 2a,2a], which is corrected as [- a,a]), where a decreases linearly in the iterative process. When a is in the interval [- 1,1], the next position of the Search Agent can be anywhere between the current gray wolf and the prey.
5) Gray wolves mainly rely on hunting for prey , ,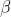 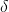To find prey. They began to search for prey location information scattered, and then concentrated to attack prey. For the establishment of the decentralized model, the search agent is kept away from the prey by ｜ > 1. This search method enables GWO to conduct global search. Another search coefficient in GWO algorithm is C. According to the formula in 2), C vector is A vector composed of random values in the interval range [0,2], and this coefficient provides random weight for prey to increase (｜ C ｜ > 1) or decrease (｜ C ｜ < 1). This helps GWO show random search behavior in the optimization process to avoid the algorithm falling into local optimization. It is worth noting that C does not decline linearly. C is A random value in the iterative process. This coefficient is conducive to the algorithm jumping out of the local, especially in the later stage of the iteration.
2, Grey wolf optimization algorithm with improved nonlinear convergence
Aiming at the disadvantages of premature convergence and easy to fall into local optimization in solving complex optimization problems, an improved gray wolf optimization algorithm (CGWO) is proposed to solve unconstrained optimization problems Firstly, the algorithm uses the reverse learning method with chaotic mapping strategy to initialize the individual population, which lays the foundation for the global optimization of the algorithm; From the point of view of balancing global and local search ability, an improved nonlinear function form is proposed for the decreasing form of convergence factor; In order to avoid the algorithm falling into local optimization, Cauchy mutation operation is performed on the current optimal gray wolf individual position The specific implementation steps of the improvement are given, and the simulation experiments are carried out on 8 standard test functions. The experimental results show that the improved gray wolf optimization algorithm has better solution accuracy and stability
3, Partial code
% Grey Wolf Optimizer
function [Alpha_score,Alpha_pos,Convergence_curve]=GWO(SearchAgents_no,Max_iter,lb,ub,dim,fobj)
% initialize alpha, beta, and delta_pos
Alpha_pos=zeros(1,dim);
Alpha_score=inf; %change this to -inf for maximization problems
Beta_pos=zeros(1,dim);
Beta_score=inf; %change this to -inf for maximization problems
Delta_pos=zeros(1,dim);
Delta_score=inf; %change this to -inf for maximization problems
%Initialize the positions of search agents
Positions=initialization(SearchAgents_no,dim,ub,lb);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%TRANSFORM HERE BY EQ1%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
Convergence_curve=zeros(1,Max_iter);
l=0;% Loop counter
%%%%%%%%%%%%%%%%%%%%%%%%%%%%EVALUAGE J HERE F?RST FOR ALL X? EQ2%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Main loop STEP 3
while l<Max_iter
for i=1:size(Positions,1)
% Return back the search agents that go beyond the boundaries of the search space
Flag4ub=Positions(i,:)>ub;
Flag4lb=Positions(i,:)<lb;
Positions(i,:)=(Positions(i,:).*(~(Flag4ub+Flag4lb)))+ub.*Flag4ub+lb.*Flag4lb;
% Calculate objective function for each search agent
fitness=fobj(Positions(i,:));
% Update Alpha, Beta, and Delta
if fitness<Alpha_score
Alpha_score=fitness; % Update alpha
Alpha_pos=Positions(i,:);
end
if fitness>Alpha_score && fitness<Beta_score
Beta_score=fitness; % Update beta
Beta_pos=Positions(i,:);
end
if fitness>Alpha_score && fitness>Beta_score && fitness<Delta_score
Delta_score=fitness; % Update delta
Delta_pos=Positions(i,:);
end
end
a=2-l*((2)/Max_iter); % a decreases linearly fron 2 to 0
% Update the Position of search agents including omegas
for i=1:size(Positions,1)
for j=1:size(Positions,2)
r1=rand(); % r1 is a random number in [0,1]
r2=rand(); % r2 is a random number in [0,1]
A1=2*a*r1-a; % Equation (3.3)
C1=2*r2; % Equation (3.4)
D_alpha=abs(C1*Alpha_pos(j)-Positions(i,j)); % Equation (3.5)-part 1
X1=Alpha_pos(j)-A1*D_alpha; % Equation (3.6)-part 1
r1=rand();
r2=rand();
A2=2*a*r1-a; % Equation (3.3)
C2=2*r2; % Equation (3.4)
D_beta=abs(C2*Beta_pos(j)-Positions(i,j)); % Equation (3.5)-part 2
X2=Beta_pos(j)-A2*D_beta; % Equation (3.6)-part 2
r1=rand();
r2=rand();
A3=2*a*r1-a; % Equation (3.3)
C3=2*r2; % Equation (3.4)
D_delta=abs(C3*Delta_pos(j)-Positions(i,j)); % Equation (3.5)-part 3
X3=Delta_pos(j)-A3*D_delta; % Equation (3.5)-part 3
Positions(i,j)=(X1+X2+X3)/3;% Equation (3.7)
end
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%EVALUAGE J HERE F?RST FOR ALL X? EQ2%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
l=l+1;
Convergence_curve(l)=Alpha_score;
end
4, Simulation results
The value of the coefficient k kk affects the nonlinear convergence factor a aa, and then affects the performance of the improved algorithm. By changing the nonlinear adjustment coefficient k = {1,1.25,1.5,1.75,2} five groups of different values for numerical experiments, the influence of the adjustment coefficient K on the performance of CGWO algorithm is analyzed from the aspect of stability.
Parameter setting: population size N = 70, maximum iteration times t m a x = 500, 30 independent runs. Take F3 as an example.
The maximum, minimum, average and standard deviation when k = 1 are:
k=1 CGWO: Maximum: 1.9788e-12,minimum value:1.0312e-15,average value:1.4892e-13,standard deviation:3.7775e-13
The maximum, minimum, average and standard deviation at k = 1.25 are:
k=1.25 CGWO: Maximum: 1.4261e-13,minimum value:4.1941e-18,average value:1.4483e-14,standard deviation:2.9773e-14
The maximum, minimum, average and standard deviation at k = 1.5 are:
k=1.5 CGWO: Maximum: 3.3684e-14,minimum value:2.5503e-17,average value:7.4339e-15,standard deviation:1.0077e-14
The maximum, minimum, average and standard deviation at k = 1.75 are:
k=1.75 CGWO: Maximum: 6.2523e-14,minimum value:1.157e-17,average value:6.7363e-15,standard deviation:1.3215e-14
The maximum, minimum, average and standard deviation at k = 2 are:
k=2 CGWO: Maximum: 7.2156e-14,minimum value:3.1809e-17,average value:4.5632e-15,standard deviation:1.2155e-14
Comprehensive analysis shows that the performance is the best when k = 2
5, References
[1] On invention, Zhao Junjie, Wang Qi Research on Grey Wolf optimization algorithm with improved nonlinear convergence [J]. Microelectronics and computer, 2019, 36 (5): 89-95
